粗颗粒矿石在提升管道内的旋转特性

唐达生，宋跃文，朱小军，夏建新，肖红



粗颗粒矿石在提升管道内的旋转特性

唐达生1，宋跃文2，朱小军2，夏建新3，肖红1

(1. 长沙矿冶研究院有限责任公司深海矿产资源开发利用技术国家重点实验室，湖南长沙，410012；2. 中南大学能源科学与工程学院，湖南长沙，410083；3. 中央民族大学生命与环境科学学院，北京，100081)

采用高速摄影技术对锰结核、富钴结壳、多金属硫化物和模拟结核粗颗粒矿石在提升管道内的旋转特性进行研究，根据粗颗粒矿石特征信息得到颗粒转速信息，以颗粒圆度()表征颗粒形状，得到粗颗粒矿石旋转速度计算公式。研究结果表明：粗颗粒矿石旋转速度随提升管道内水流速度和颗粒圆度的增大而增大，随颗粒粒度和密度的增大而减小；由粗颗粒矿石旋转速度计算公式所得旋转速度与试验结果较吻合，该公式可用于提升管道粗颗粒矿石水力输送机理研究。

提升管道；粗颗粒；旋转速度；提升速度

在粗颗粒矿石提升管道水力输送中，若管道断面流速不均匀，则颗粒将沿颗粒运动方向产生旋转，由此产生Magnus作用力。颗粒旋转与不产生旋转的运动状态有很大不同，颗粒旋转不仅影响自身的运动状态，而且干扰周围水流连续相流场，使颗粒与颗粒、颗粒与管壁之间产生碰撞，有可能增大输送能耗[1−2]，这对粗颗粒矿石提升管道水力输送不利。在颗粒旋转特性研究方面，TSUJI等[3]采用高速摄影技术对颗粒粒度为5 mm的塑料球进行分析，测得从一定高度下落到斜坡上反弹后的转速为34~70 r/s。惠遇甲等[4]使用Pentazet−35型高速摄影仪观察到泥沙颗粒始终绕着平行于床面轴旋转，得到不同运动形式时颗粒旋转速度为28.9~49.1 r/s，试验拍摄帧频为60~300 帧/s。WU等[5]采用图像分析法对循环流化床内直径为300~800 μm的玻璃球旋转特性进行研究，得到了颗粒在炉内不同位置的平均转速，颗粒转速与粒度、形状及运动速度有关，不规则颗粒的转速明显比规则颗粒的转速大。HAO等[6]研究了直径为75 μm催化剂颗粒旋转对上升管内气体和颗粒流动的影响，认为颗粒自身旋转对上升管内颗粒的速度场和浓度场有很大影响。已有研究主要针对塑料球和泥沙等细颗粒。不同物料有不同的旋转速度，随着深海采矿技术的发展，人们对粗颗粒矿石提升管道水力输送技术进行了研究[7−11]。到目前为止，人们对粗颗粒矿石在提升管道内旋转特性研究很少。为此，本文作者采用高速摄影技术和图像处理方法，对粒度为30，40和 50 mm的锰结核、富钴结壳、多金属硫化物和模拟结核颗粒在提升管道内旋转特性进行研究，研究颗粒粒度、密度和形状在不同提升流速条件下对旋转速度的影响，得到粗颗粒矿石旋转速度计算式。

1 试验装置与方法

1.1 试验装置

粗颗粒矿石旋转速度试验装置如图1所示[12]。该试验装置串联在高度为30 m的垂直管道水力提升试验系统中，采用直径为200 mm、高度为4 m的有机玻璃管(下端安装长×宽为5 mm×5 mm金属丝格筛)。有机玻璃管下部的提升管道安装了电磁流量计和提升泵，通过变频器调节泵的转速，可对提升管道内的清水流速进行调节，水流速度采用电磁流量计测量。在距有机玻璃管的4 m处布置1台2F04高速相机，全幅分辨率为2 320×1 720像素，帧率为190 帧/s，最高单场曝光时间为1/500 000 s；相机USB3.0接口直接与计算机相连，采用运动图像Tracker跟踪软件对高速相机拍摄的视频文件对颗粒轨迹进行跟踪和分析处理。

1—清水泵；2—水箱；3—给水管；4—溢流管；5—稳压管；6—回流管；7—提升管；8—稳压水箱；9—分配箱；10—标定箱；11—有机玻璃管；12—高速相机；13—流量计；14—变频器；15—计算机；16—提升泵；17—料仓；18—水包；19—地面。

1.2 试验方法

试验前，将提升管道内充满清水，颗粒投放到有机玻璃管下端的金属丝格筛上。试验时，逐渐调节提升管道内水流速度，水流就会载着颗粒由静止转入向上运动状态；当管道断面水流速度不均匀时，颗粒在向上运动过程中将会产生旋转。随着水流速度进一步增大，颗粒旋转速度相应增加，记录此时提升管道内水流速度，可得到不同提升流速下的颗粒旋转速度。粗颗粒物料性能与试验条件见表1。

表1 试验物料性能与试验条件

2 颗粒旋转运动分析

颗粒在提升管流中运动，主要受到重力、浮力、侧向力和拖拽力的作用，颗粒受力状态如图2所示。图2中：D为球形颗粒所受拖拽力；Di和Dr为非球形颗粒规则处所受拖拽力，Di＞Dr；为重力；B为浮力；t为紊动力；M为Magnus作用力，w为靠近管壁的水流速度，c为靠近管中心的水流速度。对于密度比提升介质密度大的颗粒，水流必须达到一定速度，使水流对颗粒的浮力和拖拽力足以克服颗粒的重力，颗粒才能在水流的带动下向上运动。受边界层的影响，在提升管内上升运动过程中，颗粒两侧的水流速度w和c不同，颗粒靠近管中心一侧的水流速度比靠近管壁一侧的水流速度大，其拖拽力也大，使颗粒产生旋转。进一步加大两侧的速度差，同时产生Magnus作用力M，将颗粒推向管道中心；另一方面，横向紊流脉动速度产生的紊动力t会使颗粒产生向管壁运动的趋势。但管壁附近的速度梯度大，M＞t，颗粒最终将向管道中心方向移动，在管壁处形成水环[13]。

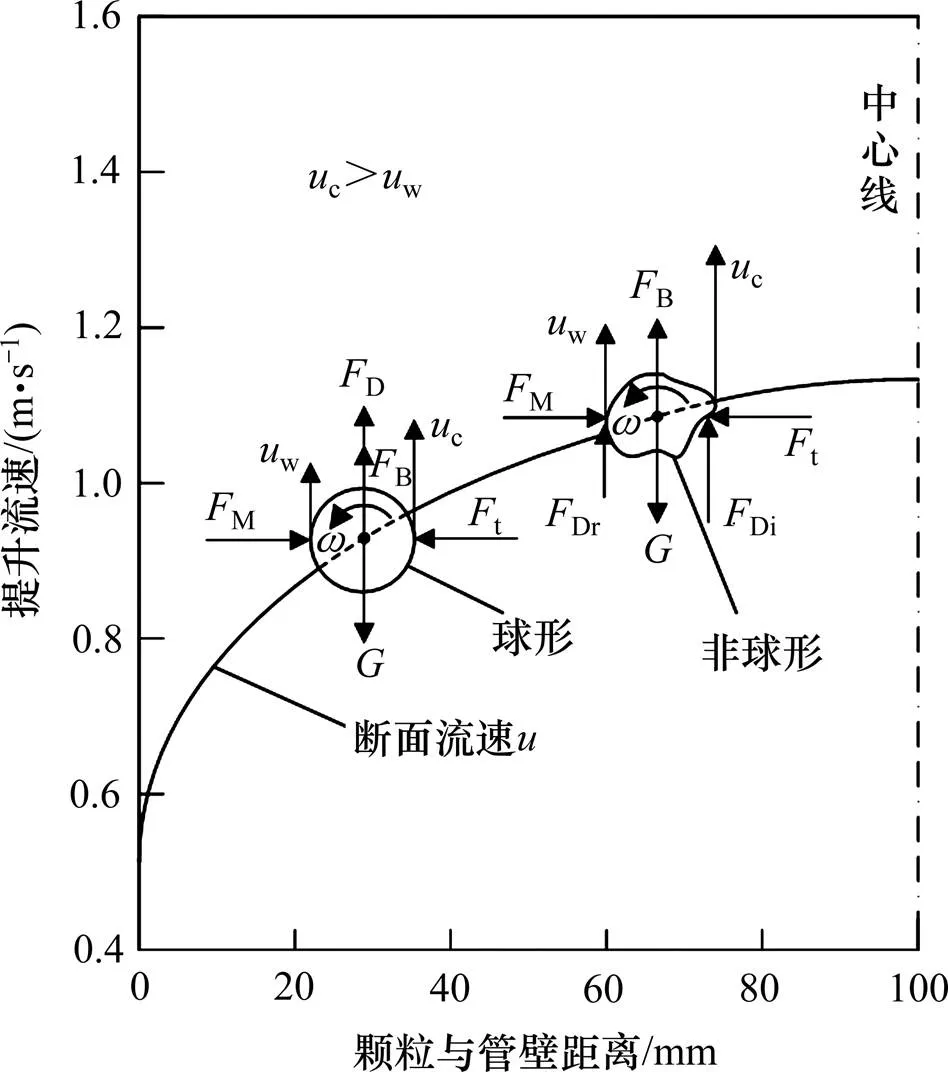
图2 颗粒受力状态

由图2可知：若不考虑颗粒碰撞作用，则作用在颗粒上的重力、浮力、拖拽力及Magnus力可表示如下。

重力：

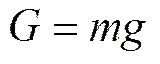
浮力B：

(2)

拖拽力D：

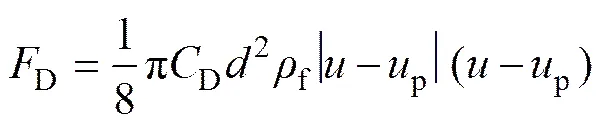
Magnus力M：

(4)

式中：为颗粒质量，kg；为重力加速度，m/s2；f为水密度，kg/m³；P为颗粒体积，m³；D为阻力系数；为球形颗粒直径，m；为水流速度，m/s；p为颗粒速度，m/s；为颗粒转速，rad/s。锰结核、富钴结壳、多金属硫化物和模拟结核与球形颗粒不同，其形状不规则。在提升管流中运动除了边界层作用外，还将受到拖拽力D作用，由于管道断面存在速度梯度，颗粒两侧流体对颗粒的拖拽力不同。颗粒两侧受到的拖拽力随颗粒受力面积的增大而增大，形状不规则颗粒处的受力面积比规则处颗粒的受力面积大，所受到的拖拽力也大，即Di＞Dr。当Di＞Dr时，颗粒将会绕颗粒质心产生扭矩，这种扭矩的存在同样使颗粒产生旋转。

3 数据处理方法

3.1 颗粒形状分析

对不规则的颗粒形状，颗粒形状描述方式有3 种[14]，即圆球度(sphericity)、圆度(roundness)和表面度(roughness)，图3所示为颗粒形状特征。颗粒形状特征参数不同，对颗粒流动特性产生的影响也不同。经分析，圆度描述形状不规则的颗粒，适用于两维图像中颗粒分析。因此，采用圆度表征锰结核、富钴结壳、多金属硫化物和模拟结核的颗粒形状，建议采用如下圆度计算公式：

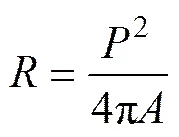
式中：为圆度；为颗粒周长，m；为颗粒面积，m2。当颗粒为球形时，=1；当颗粒不规则时，＞1。

为了分析颗粒形状在提升管流中对颗粒旋转特性的影响，使用image pro plus软件对锰结核、富钴结壳、多金属硫化物和模拟结核颗粒粒度为30, 40, 50 mm共60个颗粒进行圆度分析计算，所得结果见图4。从图4可以看出：颗粒圆度与粒度无关，颗粒圆度越大，形状越不规则。形状不规则的锰结核、富钴结壳和多金属硫化物的圆度约为1.35，不规则球形的模拟结核的圆度约为1.1。

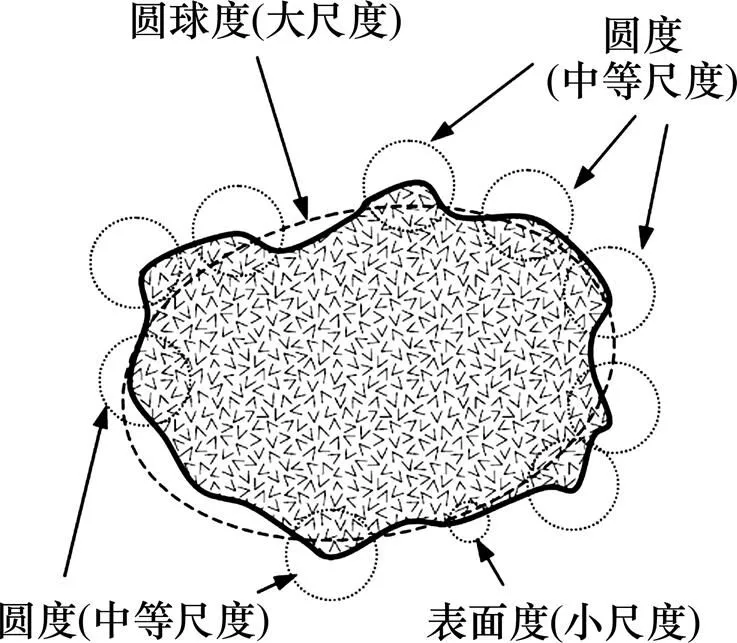
图3 颗粒形状特征

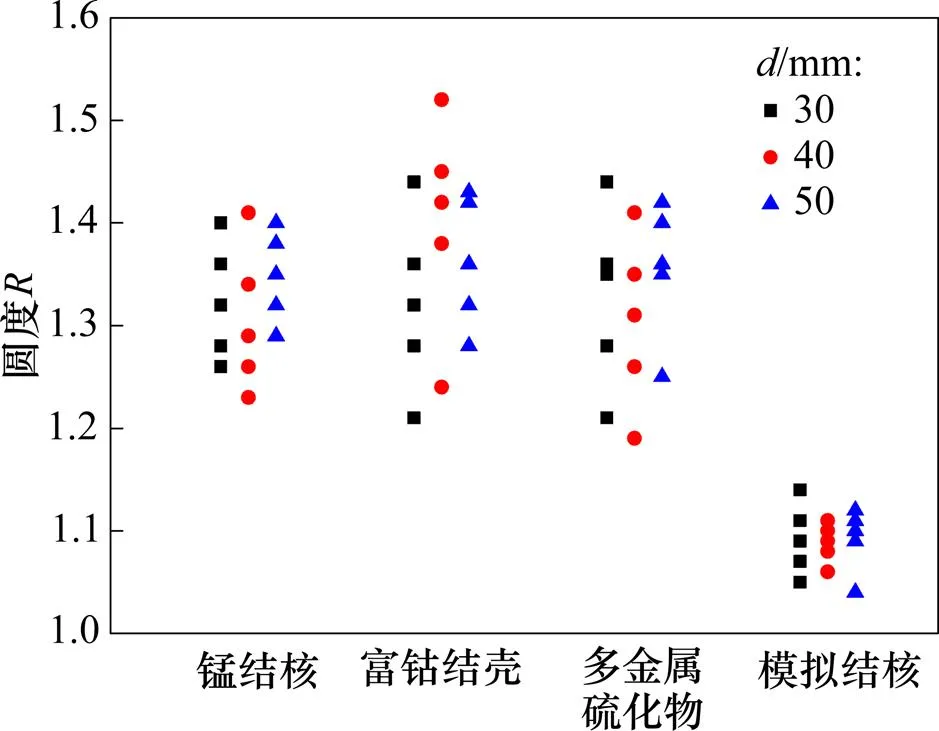
图4 颗粒圆度分布

3.2 颗粒旋转速度分析

在视频中的目标颗粒区域内，寻找表面带有“凸”点(或黑斑)的颗粒。分析颗粒在旋转过程中相邻图片颗粒“凸”点(或黑斑)的变化情况，可以得到颗粒的旋转信息。为了得到颗粒的旋转速度，通过目标颗粒旋转时间序列图上的颗粒特征角度变化，求出颗粒的旋转速度。图5所示为不同时间的颗粒旋转角度示意图，具体处理步骤如下：

1) 使用tracker颗粒追踪软件将高速相机拍摄的视频文件输出为图像文件。

2) 选取特征点，颗粒转轴垂直于拍摄面内。

3) 使用Photoshop软件对序列图内颗粒的中点和颗粒的特征点连成1条直线，得该直线和水平线之间的夹角1。在该颗粒其他序列图中重复此步骤，得到2，3，4和5。

4) 对应时间序列上的转角变化信息，得到颗粒在时间序列上的转速0,，1，2和3。

5) 对0，1，2和3求平均值，可得到颗粒旋转速度。

为了保证计算精度，不能取相邻帧数的图像作为颗粒的序列图。取5组图像求解颗粒旋转速度，颗粒旋转速度采用下列公式计算：

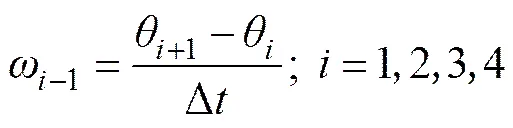
(7)

(8)

3.3 颗粒旋转速度验证

为了确保颗粒旋转速度分析方法的正确性，有必要对颗粒旋转速度计算方法进行验证。

对于球形颗粒，水流对颗粒在旋转过程中产生的作用扭矩为

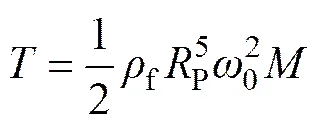
由角速度能量守恒可以得到：

(11)

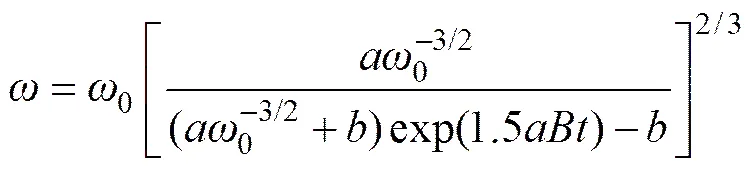
式中：，和为与颗粒、流体性质相关的系数；为旋转速度，rad/s；0为初始旋转速度，rad/s；；；；f为水运动黏性系数，m2/s；为水密度，kg/m3；为颗粒密度，kg/m3；对于不规则形颗粒，引入颗粒圆度进行修正，修正后的颗粒旋转速度随时间的变化公式如下：

(13)

式中：为圆度，对锰结核，取=1.35；对模拟结核，取=1.1。

对粒度为30，40和50 mm锰结核和模拟结核颗粒进行验证，颗粒的旋转速度与时间的关系如图6所示。由图6可以看出：试验得到颗粒在时间序列上的旋转转速(0，1，2和3)与式(13)计算得到的颗粒旋转转速的变化曲线基本相同，说明颗粒旋转速度分析处理方法是正确的。

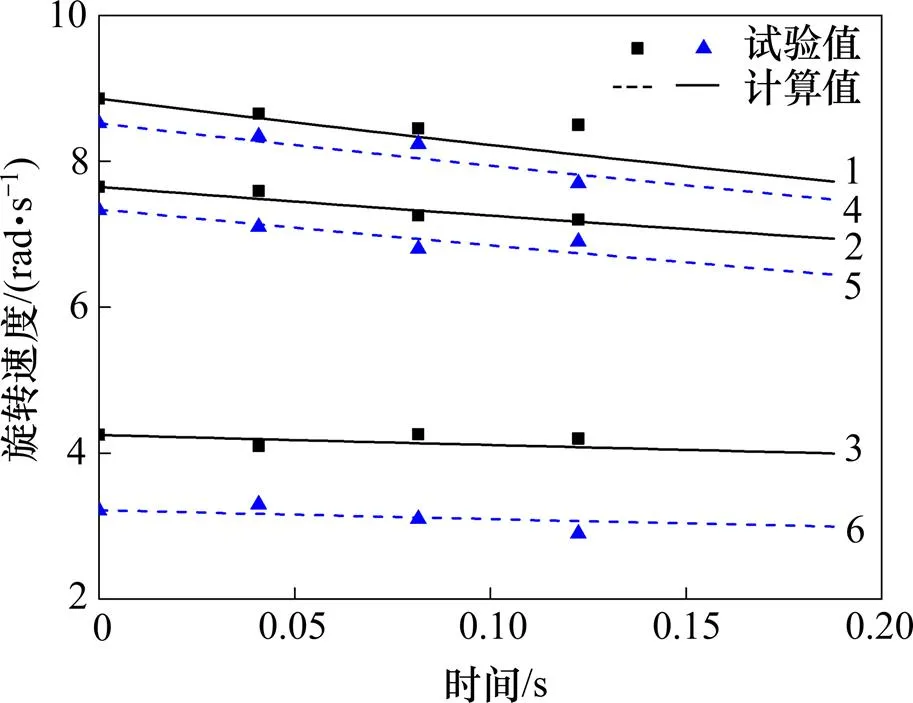
颗粒粒度/mm：1—30(锰结核)；2—40(锰结核)；3—50(锰结核)；4—30(模拟结核)；5—40(模拟结核)；6—50(模拟结核)。

4 试验结果与分析

对锰结核、富钴结壳、多金属硫化物和模拟结核在提升管道内进行粗颗粒矿石旋转速度测试。由于颗粒在提升管内的旋转受到的不确定因素较多，如颗粒与颗粒、颗粒与管壁之间发生碰撞[16−17]，为了使问题简化，本文不考虑颗粒碰撞因素，研究颗粒粒度、密度和形状在不同提升流速下对旋转速度的影响。

4.1 粒度对旋转速度的影响

锰结核、富钴结壳、多金属硫化物和模拟结核颗粒粒度为30，40和50 mm时不同粒度的颗粒旋转速度与提升流速的关系如图7所示。从图7可以看出：4种物料的颗粒旋转速度均随提升流速增大而增大；在相同流速下，颗粒旋转速度随颗粒粒度的增大而减小。这是因为粒度较小的颗粒在旋转过程中，受到水流对其产生的阻碍扭矩较小，较小粒度的颗粒更容易维持在较高转速状态。

4.2 密度对旋转速度的影响

锰结核、富钴结壳、多金属硫化物和模拟结核4种不同密度的颗粒旋转速度与提升流速的关系如图8所示。由图8可以看出：4种物料的颗粒旋转速度均随提升流速的增加而增加；在相同流速下，颗粒旋转速度随颗粒密度的增大而变小，这与颗粒粒度对旋转速度的影响规律基本上相同。但颗粒粒度=30 mm的锰结核、富钴结壳和多金属硫化物的旋转速度随提升流速的变化趋势十分接近，这可能是对于密度和粒度均较小的颗粒，水流对其产生的扭矩基本相等所致。模拟结核密度较大，颗粒旋转速度较低。

4.3 形状对旋转速度的影响

锰结核、富钴结壳和多金属硫化物颗粒属不规则形，其圆度为1.35左右，模拟结核属不规则球形，其圆度为1.1左右。为了分析颗粒形状对旋转速度的影响，对不规则形的锰结核和不规则球形的模拟结核进行对比。2种物料颗粒的旋转速度、圆度随提升流速的关系如图9所示。从图9可以看出：由于锰结核的圆度大于模拟结核的圆度，在同一种提升流速下，同一种粒度的锰结核旋转速度比同一种粒度的模拟结核旋转速度大。锰结核旋转速度较大可能是颗粒在提升水流中受力不均匀所致，颗粒受力不均匀产生的扭矩使颗粒更加容易旋转，甚至在没有速度梯度的流场中，也有可能产生旋转现象。

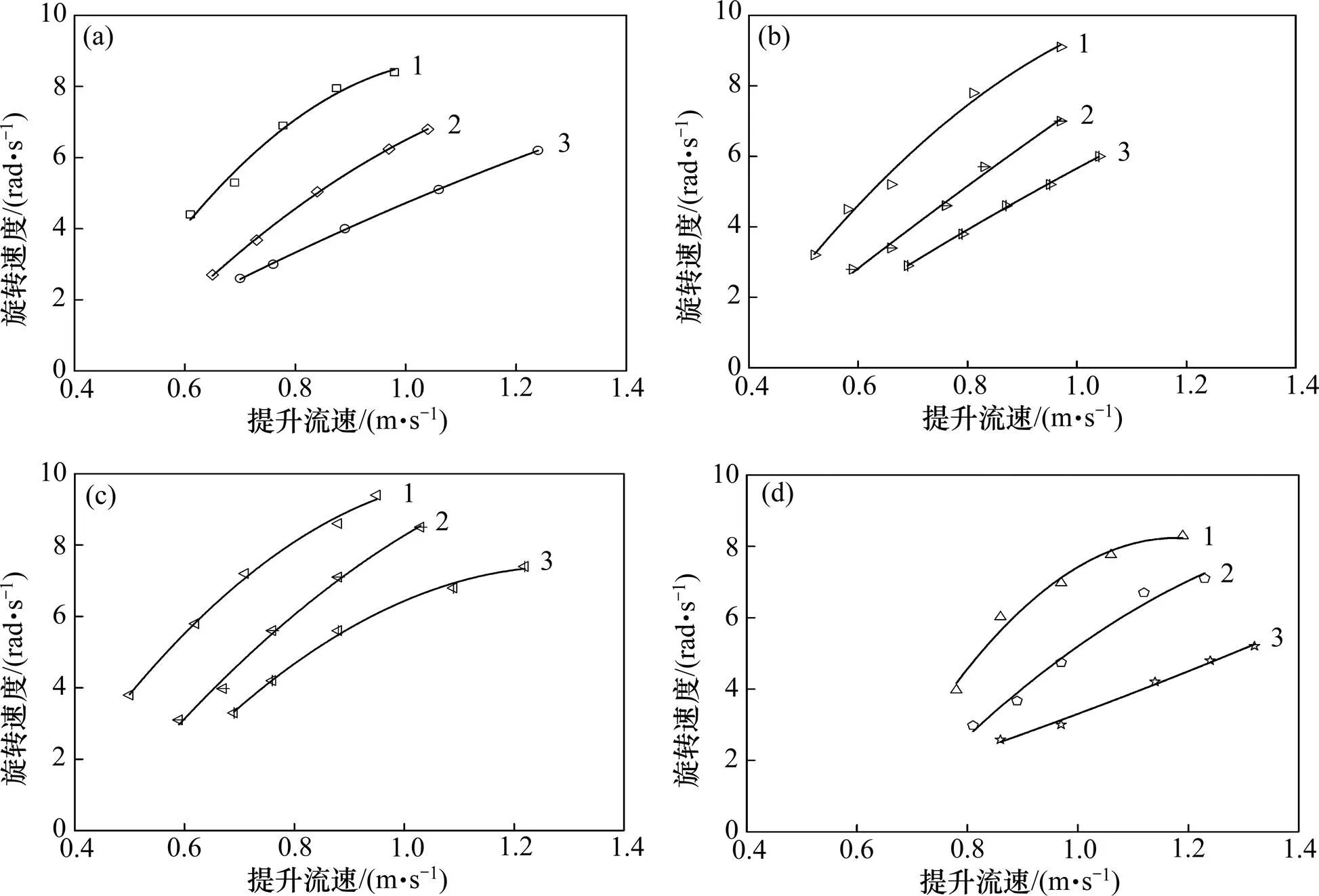
(a) 锰结核；(b) 富钴结壳；(c) 多金属硫化物；(d) 模拟结核

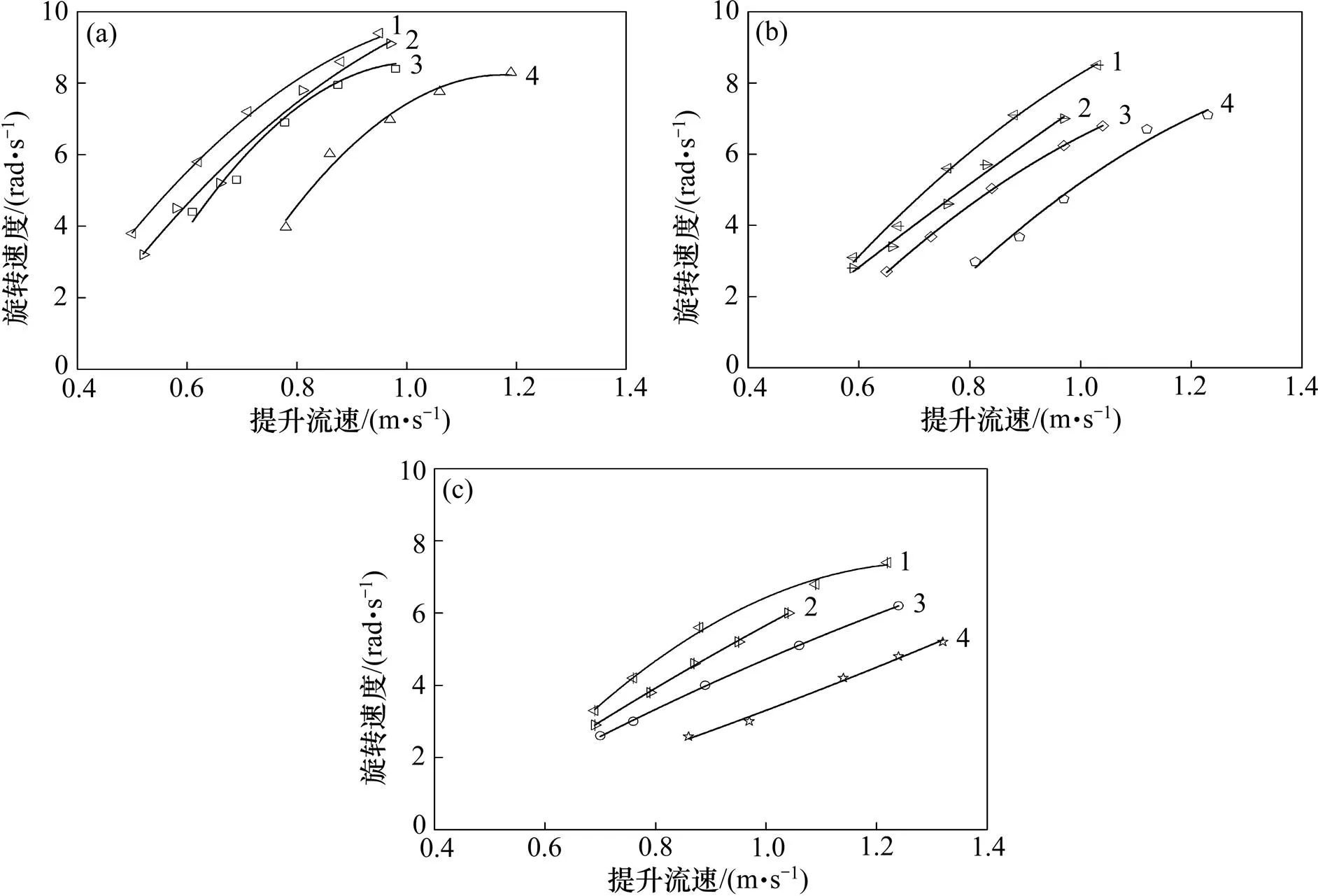
颗粒粒度d/mm：(a) 30；(b) 40；(c) 50。

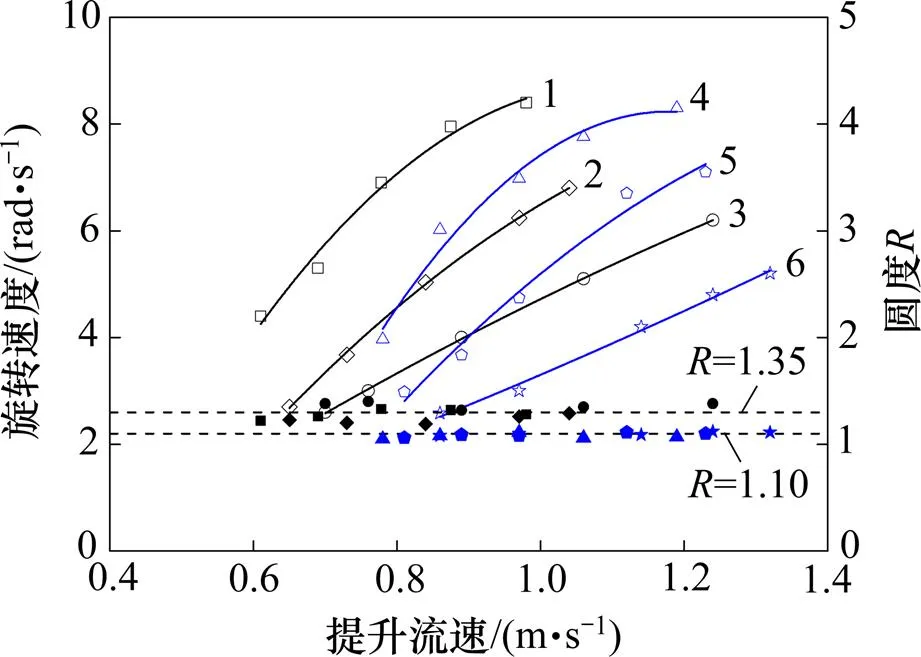
颗粒粒度/ mm：1—30(锰结核)；2—40(锰结核)；3—50(锰结核)；4—30(模拟结核)；5—40(模拟结核)；6—50(模拟结核)。

4.4 旋转速度回归计算

为了定量分析颗粒旋转速度与提升流速的关系，考虑到粒度、密度和圆度，采用1stopt软件对试验结果进行多元非线性拟合，取收敛误差≤1.0×10−10，锰结核、富钴结壳、多金属硫化物和模拟结核颗粒旋转速度的经验公式为：

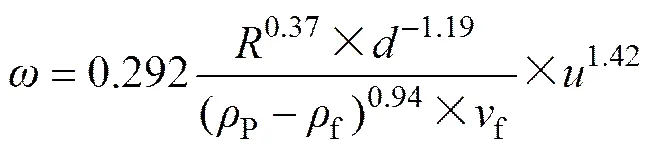
从式(14)可以看出：颗粒旋转速度随提升流速和圆度的增大而增大，随颗粒粒度和密度的增大而减小，这与试验结果一致。图10所示为颗粒旋转速度计算结果与实测结果对比，计算结果与实测结果基本吻合，其相对误差在±15％以内。

5 结论

1) 对提升管流内颗粒产生旋转运动进行分析，引入颗粒圆度表征颗粒形状，使用tracker软件对颗粒轨迹进行追踪，对颗粒旋转速度进行验证，结果表明颗粒旋转速度测试方法是可行的。

2) 锰结核、富钴结壳、多金属硫化物和模拟结核的颗粒旋转速度均随提升流速的增大而增大；在相同流速下，颗粒旋转速度随颗粒粒度和颗粒密度的增大而减小。在相同提升流速和粒度下，锰结核的旋转速度比模拟结核的旋转速度大。

3) 对试验数据进行多元非线性拟合，得到了粗颗粒矿石旋转速度与提升流速、粒度、密度和圆度的关系式；颗粒旋转速度计算结果与实测结果相对误差在±15％以内。

[1] CHEN J, JIN G, ZHANG J. Large eddy simulation of orientation and rotation of ellipsoidal particles in isotropic turbulent flows[J]. Journal of Turbulence, 2015, 17(3): 1−19.

[2] NJOBUENWU D, FAIRWEATHOR M. Dynamics of single, non-spherical ellipsoidal particles in a turbulent channel[J]. Chemical Engineering Science, 2015, 123: 265−282.

[3] TSUJI Y, MORIKAWA Y, MIZUNO O. Experimental measurement of the Magnus force on a rotating sphere at low Reynolds numbers[J]. Journal of Fluids Engineering, 1985, 107(3): 484−488.

[4] 惠遇甲, 胡春宏. 水流中颗粒跃移的运动学特征[J]. 水利学报, 1991(12): 59−64. HUI Yujia, HU Chunhong. Saltation characteristics of particle motions in water[J]. Journal of Hydraulic Engineering, 1991(12): 59−64.

[5] WU Xuecheng, WANG Qinhui, LUO Zhongyang. Experimental study of particle rotation characteristics with high-speed digital imaging system[J]. Powder Technology, 2008, 181(1): 21−30.

[6] HAO Zhenhua, WANG Shuai, LU Huilin. Numerical simulation of fluid dynamics of a riser: influence of particle rotation[J]. Industrial and Engineering Chemistry Research, 2010, 49(8): 3585−3596.

[7] BLACNBURN J, HANRAHAN S. Offshore production system definition and cost study[R]. Sydney: Nautilus Minerals Inc, 2010: 164−173.

[8] CHI H Y, JONG M P, JUNG S K, et al. Shallow lifting test for the development of deep ocean mineral resources in Korea[C]// Proceedings of the Ninth (2011) ISOPE Ocean Mining Symposium. Hawaii, USA, 2011: 149−152.

[9] YANG Ning, CHEN Guangguo, TANG Dasheng. Behavior of single particle and group particles in vertical lifting pipe in China[C]// Proceedings of the Ninth (2011) ISOPE Ocean Mining Symposium. Hawaii, USA, 2011: 153−157.

[10] YAMAZAKI T, NAKATANI N, ARAI R. How to improve economy of seafloor massive sulfide mining under Japan’s Conditions[C]// Presentation for UMI 2012. Shanghai, China: Underwater Mining Institute, 2012: 1−23.

[11] 唐达生, 阳宁, 金星. 深海粗颗粒矿石垂直管道水力提升技术[J]. 矿冶工程, 2013, 33(5): 1−8. TANG Dasheng, YANG Ning, JIN Xing. Hydraulic lifting technique with vertical pipe for deep-sea coarse mineral particles[J]. Mining and Metallurgical Engineering, 2013, 33(5): 1−8.

[12] 阳宁, 唐达生, 何端阳, 等. “十五”深海采矿扬矿系统实验室试验研究报告[R]. 长沙: 长沙矿冶研究院, 2007: 8−19. YANG Ning, TANG Dasheng, HE Duanyang, et al. The study on lift system in deep ocean mining of the tenth five-year plan[R]. Changsha: Changsha Research Institute of Mining and Metallurgy, 2007: 8−19.

[13] ENGELMANN H E. Vertical hydraulic lifting of large-size particle-a contribution to marine mining[C]//Offshore Technology Conference. Houston, USA: OTC, 1978: 731−740.

[14] MITCHELL J K, SOGA K. Fundamentals of soil behavior[M]. 3rd ed. New York: John Wiley & Sons, 2005: 87−89.

[15] DENNIS S C R, SINGH S N, INGHAM D B. The steady flow due to a rotating sphere at low and moderate Reynolds numbers[J]. Journal of Fluid Mechanics, 1980, 101(2): 257−279.

[16] 杨秋辉. 气固流化床内颗粒旋转与碰撞特性的实验研究[D]. 杭州: 浙江大学热能工程研究所, 2012: 39−51. YANG Qiuhui. Experiments on particle rotation and collision in gas-solid fluidizing beds[D]. Hangzhou: Institute for Thermal Power Engineering of Zhejiang University, 2012: 39−51.

[17] 李斌, 宋小龙. 流化床内颗粒旋转特性的数值模拟[J]. 动力工程学报, 2014, 34(3): 189−195. LI Bin, SONG Xiaolong. Numerical simulation on rotating characteristics of particles in fluidized bed[J]. Journal of Chinese Society of Power Engineering, 2014, 34(3): 189−195.

(编辑 陈灿华)

Rotation behavior of coarse-particle ores in lifting pipe

TANG Dasheng1, SONG Yuewen2, ZHU Xiaojun2, XIA Jianxin3, XIAO Hong1

(1. Changsha Research Institute of Mining and Metallurgy Co. Ltd., State Key Laboratory of the Exploration and Utilization of Deep-sea Mineral Resources, Changsha 410012, China;2. School of Energy Science and Engineering, Central South University, Changsha 410083, China;3. College of Life and Environmental Sciences, Minzu University of China, Beijing 100081, China)

High speed photograph technique was used to characterize the rotation behavior of coarse-particle ores in a lifting pipe, including manganese nodules, cobalt-rich crust, poly-metallic sulfide and simulation nodules. For those ores, the rotation speed was calculated based on their features, and the shape was characterized by their roundness. A fitting equation for the rotation speed of the ores was proposed. The results show that when the lifting velocity and the roundness of the ores increase, their rotation speed increases. However, when the diameter and the density of the ores increase, their rotation speed decreases. The calculation results obtained by the fitting equation are in agreement with the experimental results, which can be used to research the hydraulic lifting pipeline system mechanism.

lifting pipe; coarse particle; rotation speed; lifting velocity

10.11817/j.issn.1672-7207.2017.07.021

TD825.6

A

1672−7207(2017)07−1831−08

2016−08−15；

2016−10−17

国家自然科学基金资助项目(51174037，51339008) (Projects(51174037, 51339008) supported by the National Natural Science Foundation of China)

唐达生，教授级高级工程师，从事深海采矿扬矿和管道输送技术研究；E-mail: Tds54@163.com