由直尺和三角板改编的中考压轴题赏析

赵立新

[摘 要] 以直尺和三角板为道具，以熟悉的几何图形为载体，并辅之以平移、旋转、翻折等变换手段衍生的一系列问题，能为学生动手实践与操作联想提供思考空间，也能提高学生的图形运动变化、分类讨论思想等综合运用能力.

[关键词] 直尺；三角板；变换；分类讨论；创新

数学课程标准倡导学生“在生动具体的情境中学习数学”“在现实的情境中体验和理解数学”. 因此，教师教学时应充分利用学生的生活经验，创设与学生生活环境密切相关且学生感兴趣的问题情境，让学生主动地进行观察﹑实验﹑猜测﹑验证﹑推理与交流等数学活动. 而直尺和三角板是学生最常见的学习工具，以直尺和三角板为道具，以熟悉的几何图形为载体，并辅之以平移、旋转、翻折等变换手段衍生一系列问题，能为学生动手实践与操作联想提供思考空间，也能提高学生对基本图形性质的掌握程度以及观察、实验、比较、联想、类比、归纳的能力和图形运动变化、分类讨论思想等综合运用的能力. 笔者改编了一道关于直尺和三角板的压轴题，并进行适当难度分析和价值梳理，以此和大家探讨关于中考复习有效性的问题，以便更好地提高数学教学有效性.

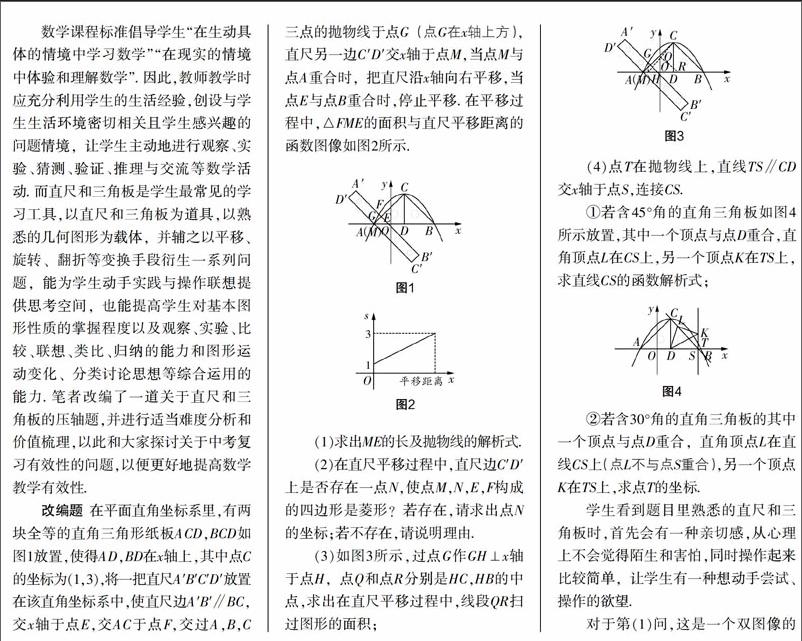
改编题 在平面直角坐标系里，有两块全等的直角三角形纸板ACD，BCD如图1放置，使得AD，BD在x轴上，其中点C的坐标为（1，3），将一把直尺A′B′C′D′放置在该直角坐标系中，使直尺边A′B′∥BC，交x轴于点E，交AC于点F，交过A，B，C三点的抛物线于点G（点G在x轴上方），直尺另一边C′D′交x轴于点M，当点M与点A重合时，把直尺沿x轴向右平移，当点E与点B重合时，停止平移. 在平移过程中，△FME的面积与直尺平移距离的函数图像如图2所示.

（1）求出ME的长及抛物线的解析式.

（2）在直尺平移过程中，直尺边C′D′上是否存在一点N，使点M，N，E，F构成的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由.

（3）如图3所示，過点G作GH⊥x轴于点H，点Q和点R分别是HC，HB的中点，求出在直尺平移过程中，线段QR扫过图形的面积；

评析 我们在平时的教学或中考复习中会发现学生对于图像的分析能力总是有所欠缺，找不准分析的方向，不能对图中所呈现的信息进行合理地分类探究，而当遇到双图像对应起来观察时就更困难了，那么如何提高学生的识图能力呢？特别是在中考复习时如何处理复杂图形的分解、分类呢？笔者在毕业班教学多年，发现教学复杂几何图形时，要让学生从最基本的条件出发，去发现、推导结论，一步一步地把每一个呈现的条件最大化挖掘，而不是把所有条件摆在一起寻找结论所需，这样学生在各个击破的前提下，其之间的联系也就自然呈现了，也就较容易找到问题的根本所在. 比如第（1）问，全等的三角板放在坐标系里，能得到什么结论？学生能得到△CAB为等腰三角形，又由点C的坐标为（1，3），可以得到OD=1，CD=3. 再由直尺边A′B′∥BC，得到△FME也为等腰三角形. 对直尺的两种特殊位置关系所产生面积的分析，可以发现直尺未走时其面积为1，停止时其面积为3，从而可以求出答案. 在平时的课堂上讲解和分析此类问题时，笔者总是用小步子的方式抛出问题，学生接招的难度明显降低，而当把所有问题抛完（甚至还没抛完，学生就发现剩余的结论就是我们所需要的）时，结论就出来了，所以小步骤讲解几何题的方法既可以提高学生学习几何的兴趣、信心，也能提高学生分析问题的针对性、连续性、完整性，还会提高中考几何压轴题的学习效率、复习效率.

评析 分类讨论是中考压轴题里的“常客”，几乎每一份中考试卷里的压轴题都有其踪迹. 这类题的特点就是小题较多，且容易失分，常常会被同学们忽略，经常忘记分类讨论，或问题经常讨论不全，讨论全了结果还不一定对. 而且，这类题往往陷阱比较多，一个不注意就会掉进出题陷阱中. 所以，这类题的出现可以考查学生对问题思路的清晰程度，对知识点的掌握程度，加强对这类题的训练，可以提高解题效率，还可以培养学生的归纳总结能力和逻辑思维能力. 那么如何分类、精准讨论呢？ 我们要有条理地对题目进行分类，比如该小题对菱形产生的情况进行分类. 由于ME的长度是固定不变的，以它为突破口，情况会有两种：ME为对角线或边. 值得注意的是，在列出所有需要讨论的可能性之后，要仔细审查是否每种可能性都会存在，是否有需要舍去某些情况.

评析 《数学课程标准》中关于几何直观的描述有“借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果”“几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥重要作用”. 在探究复杂几何图形时，分解步骤，寻找模型，是解决问题的关键所在. 当一副三角板放上去时，我们联想到“K型”三角形相似，从而得以突破难点，所以在平时的教学和中考复习中，要注意设置一些含有常见的基本图形的几何试题，培养和训练学生提炼数学模型的能力，以便在复杂的图形中排除其他条件的干扰，迅速触及问题的本质，提高解题效率，强化解题基本技能.

“提供新材料、创设新情境、提出新问题”已成为近几年中考数学试题设计的新特点，《数学课程标准》中明确指出：“学生学习要从自身已有的生活经验出发，让学生亲身经历将实际问题抽象成数学模型，并进行解释与应用的过程，倡导学生主动参与、勤于动手、乐于探究. ”如果我们在平时的教学和研究中，多关注身边学生熟悉的数学，多让学生讲解问题的由来，多研究数学知识最核心却又最简洁的那一点，数学就会成为学生喜欢学、喜欢探究、喜欢创新的一门课程.