Yang系统与Lorenz，Chen系统的光滑不等价性研究1

陈玉明

（广东技术师范学院 数学与系统科学学院, 广东 广州 510665）

Yang系统与Lorenz，Chen系统的光滑不等价性研究1

陈玉明

（广东技术师范学院 数学与系统科学学院, 广东 广州 510665）

很多的三维 Lorenz型混沌系统都具有类似的代数方程结构，然而它们所表现出来的动力学行为却不尽相同.基于系统间光滑等价性的定义，本文分别证明了具有某个混沌参数集的 Yang系统，与任意参数下的Lorenz系统及Chen系统之间均为光滑不等价的，这说明了Yang系统是一个独立的混沌系统，对其任何动力学行为的研究都是必要的.

Lorenz系统；Chen系统；Yang系统；混沌；光滑等价

一、引言

自从首个混沌数理模型，即Lorenz系统[1]

被发现以来，尤其是对这个模型本身，来自不同领域的数学家、物理学家及工程师们对混沌的产生、混沌系统的特征、分岔、通向混沌的路径及其它一些非线性科学中的相关课题展开了广泛地研究Lorenz系统进行混沌的反控制，促使了Chen系统发现，

它具有和Lorenz系统不同的特征.Lu进一步发现了另外一个新的混沌系统，被称为Lu系统

该系统可被认为是连接Lorenz系统和Chen系统的桥梁除此之外，由 Yang在 2008年所提出的Yang系统

也可以连接Lorenz系统及Chen系统，并可表示从一个系统到另一个系统的过渡.在经典参数下，Yang系统具有一个混沌吸引子、一个鞍点平衡点及两个稳定的结焦平衡点.容易看出如下系统

包含了经典的Lorenz系统、Chen系统、Lu系统及Yang系统等，这一系统常常被称为Lorenz型系统.如果将上述Lorenz型系统的线性部分及二次部分分成如下形式

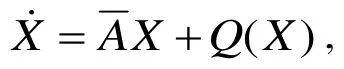
关于Lorenz型系统的研究已经获得了很多广泛而深入的结果[9-14].作为Lorenz型系统的特殊情形，Lorenz系统、Chen系统、Lu系统及Yang系统具有非常类似的代数方程结构，这就会导致一个非常基本而有趣的问题：这些系统彼此之间是否等价？在 2010年，Hou[15]证明了Lorenz系统与Chen系统之间的光滑不等价性；Lu系统与Lorenz及Chen系统的光滑不等价性在2013年被Chen[16]所证明.关于Yang系统与其余系统之间的不等价性，Chen[16]只从动力学行为差异上进行了简略的说明，而并没有严格的给出证明.在本文中，将给出Yang系统与其余系统之间的光滑不等价性证明.

二、光滑不等价性分析

是两个微分方程系统，则有如下关于光滑等价性的定义：

注 1：两个微分同胚的系统实际上是一样的，于是可以认为是通过不同坐标来表示的同一个系统.例如，两个系统对应平衡点的特征值是一样的.这是因为，如果是这样的一对对应平衡点，并且分别是对应的Jacobian矩阵，于是对方程（6）进行微分可得

图1.Lorenz系统（1）的混沌吸引子相图：

图2.Chen系统（2）的混沌吸引子相图：

图3.Yang系统（3）的混沌吸引子相图：

接下来，我们将会证明在某些混沌参数下的Yang系统，与任意参数下的Lorenz及Chen系统都光滑不等价.

即系统（4）的平衡点x 对应于系统（5）的平衡点h(x).因此，Yang系统必定要与具有相同数量平衡点的Lorenz系统之间才可能等价.接下来证明存在某些具有三个平衡点的Yang系统，它们不与任何同样具有三个平衡点的Lorenz系统光滑等价，其中Yang系统和Lorenz系统的平衡点分别如（9）和（7）所示.

今

证明：假设存在中的微分同胚，使得 Yang系统c及Chen系统下是光滑等价的，由类似于定理1的证明可知，Yang系统光滑等价于一个具有相同数量平衡点的 Chen系统.接下来证明存在某些具有三个平衡点的Yang系统，它们不与任何同样具有三个平衡点的Chen系统光滑等价，其中Yang系统和Chen系统的平衡点分别如（9）和（8）所示.

根据注1可知，有如下等式成立：

[1] LORENZ E N.Deterministic non-periodic flow [J].J.Stmos.Sci, 1963(20) : 130-141.

[2] SPARROW C.The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors [M].New York: Springer.1982.

[3] HIRSH M W, SMALE S, DEVANEY R L.Differential Equations, Dynamical Systems, and an Introduction to Chaos [M].New York: Elsevier Academic Press, 2007.

[4] CHEN G, UETA T.Yet another chaotic attractor [J].Int.J.Bifurcat.Chaos, 1999(9) : 1465-1466.

[5] LU J, CHEN G.A new chaotic attractor coined [J].Int.J.Bifurcat.Chaos, 2002(12) : 659-661.

[6] LU J, CHEN G, CHENG D.Bridge the gap between the Lorenz system and the Chen system [J].Int.J.Bifurcat.Chaos, 2002( 1 2): 2917-2926.

[7] YANG Q, CHEN G.A chaotic system with one saddle and two stable node-foci [J].Int.J.Bifurcat.Chaos, 2008(18) : 1393-1414.

[8] CELIKOVSKY S, CHEN G.On a generalized Lorenz canonical form of chaotic systems [J].Int.J.Bifurcat.Chaos, 2002(12) : 1789-1812.

[9] YANG Q, CHEN G, ZHOU T.A unified Lorenz-type system and its canonical form [J].Int.J.Bifurcat.Chaos, 2006(16) : 2855-2871.[10] LIU Y, YANG Q.Dynamics of a new Lorenz-like chaotic system [J].Nonlin.Anal.: Real World Appl, 2010(11) : 2563-2572.

[11] LIU Y.Closed orbits in the general Lorenz family [J].Int.J.Bifurcat.Chaos, 2011(21): 2583-2586.

[12] LUO Q, LIAO X, ZENG Z.Sufficient and necessary conditions for Lyapunov stability of Lorenz system and their application [J].Sci.China Ser.F-Inf.Sci, 2010(53) : 1574-1583.

[13] VISWANATH D, SAHUTOGLU S.Complex singularities and the Lorenz attractor [J].SIAM Rev, 2010(52) : 294-314.

[14] KIRIKI S, SOMA T.Parameter-shifted shadowing property for geometric Lorenz attractors [J].Trans.Amer.Math.Soc, 2004(4) : 1325-1339.

[15] HOU Z, KANG N, KONG X.etal.On the nonequivalence of Lorenz system and Chen system [J].Int.J.Bifurcat.Chaos, 2010(2) : 557-560.

[16] CHEN Y, YANG Q.The nonequivalence and dimension formula for attractors of Lorenz-type system [J]. Int.J.Bifurcat.Chaos, 2013(2 3): 1350200(12 pages).

[17] KUZNETSOV Y A.Elements of Applied Bifurcation Theory.Third Edit [M].B erlin :Springer, 2004.

[18] YANG L, ZHANG J, HOU X.Nonlinear Systems of Algebraic Equations and Mechanical Theorem Proving [M].Shanghai: Shanghai Scientific and Technological Education Publishing House.(In Chinese).

【责任编辑：吴跃新】

Research on the Smooth Nonequivalence of Yang System and Lorenz, Chen Systems

CHEN Yuming
(School of Mathematics and Systems Science, Guangdong Polytechnic Normal University, Guangzhou 510665, Guangdong, China)

Many Three dimensional Lorenz-type chaotic systems have similar forms of equation, but their dynamic behaviors are different.In this paper, based on the definition of smoothly equivalence, Yang system with a set of chaotic parameters is proved to be smoothly nonequivalent to Lorenz and Chen systems with any parameter.This means Yang system is an independent chaotic system, the research of all its dynamic behavior is necessary.

Lorenz system; Chen system; Yang system; Chaos; Smooth equivalence

A

1671 - 5934 (2017)03 - 0035 - 06

2017 - 03 - 20

国家自然科学基金（No.11626068）; 广东省自然科学基金（2015A030310424）

通讯联系：陈玉明（1987-）, 男, 江西赣州人, 讲师, 博士, 研究方向为微分方程及动力系统，E-mail: LKHPZ@126.com