非线性时滞微分方程的h-渐近稳定性1

黄明辉

（广州华夏职业学院 基础部， 广州 510935）

非线性时滞微分方程的h-渐近稳定性1

黄明辉

（广州华夏职业学院 基础部， 广州 510935）

采用Krasnoselskii不动点定理证明带可积时滞的非线性中立型微分方程零解的h-渐近稳定性.文中的结论进一步推广了Pinto and Sepulveda[4]的定理.同时，提供了一个例子加以说明所得的结果.

h-渐近稳定；large contraction；非线性

1 引言

近来，不动点理论已经成为时滞微分方程的稳定性和周期性研究的主要工具之一[1-7].例如，以下的方程

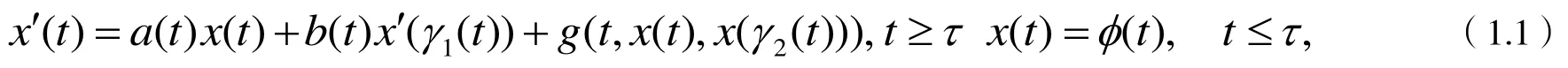
其特殊形式近年来引起了许多研究者的注意[2,4,6,7].下面，研究非线性中立型微分方程

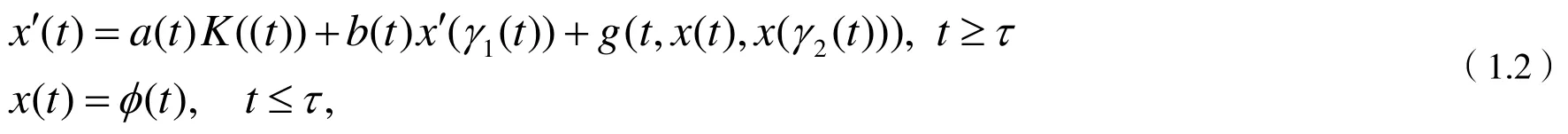
2 准备工作

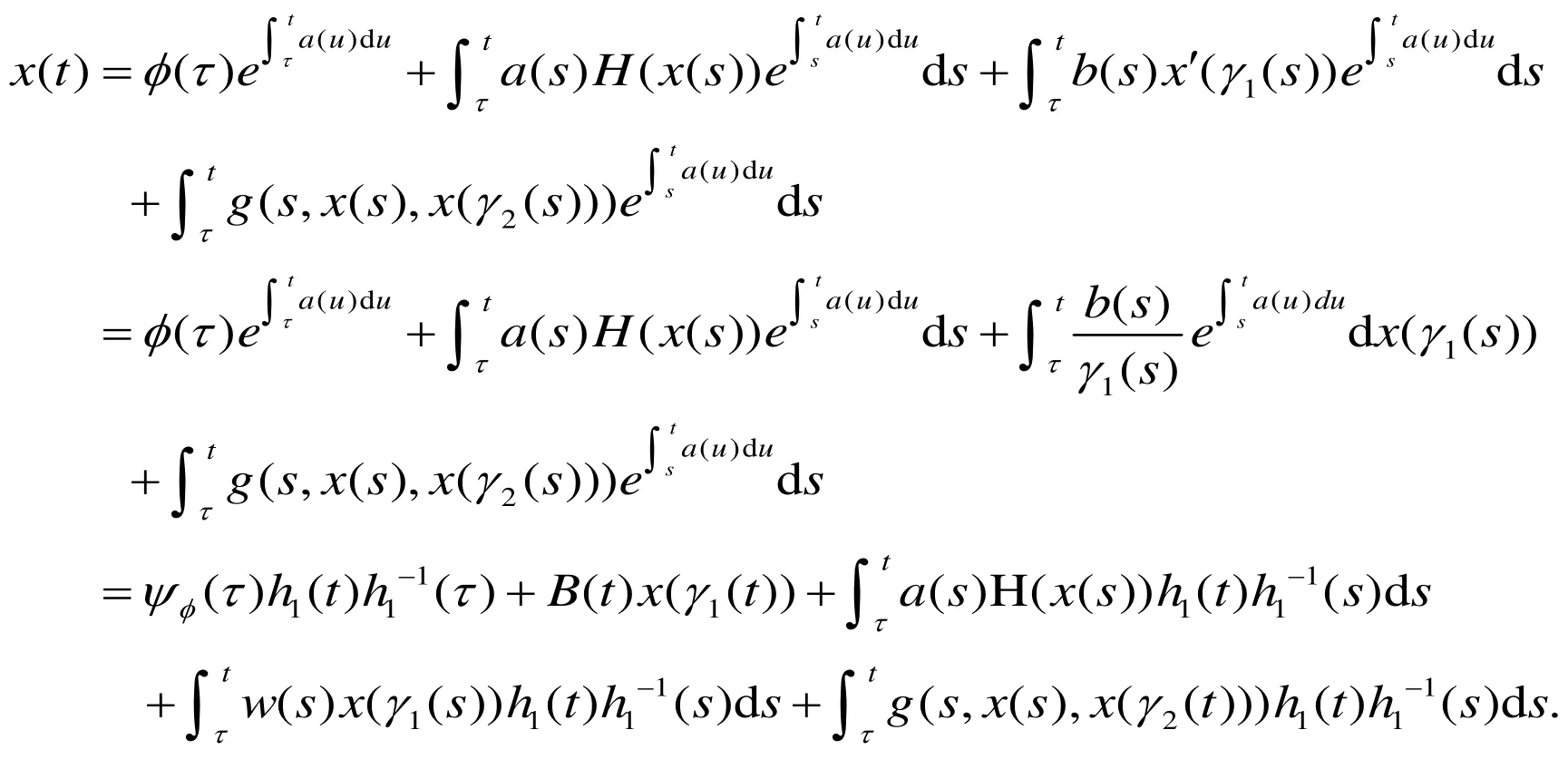
以上的过程每一步都是可逆的，证明完成.

3 主要结论

对于方程（1.2）

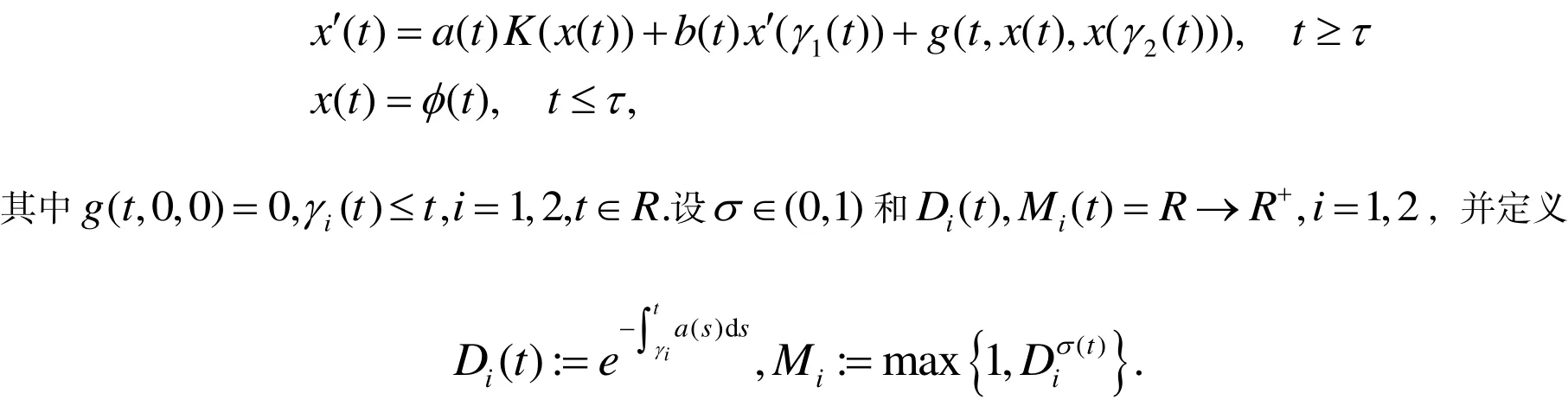
接着，假设：

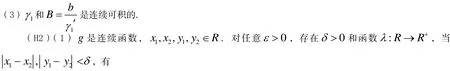
由（3.5），（3.7）和（3.8），得

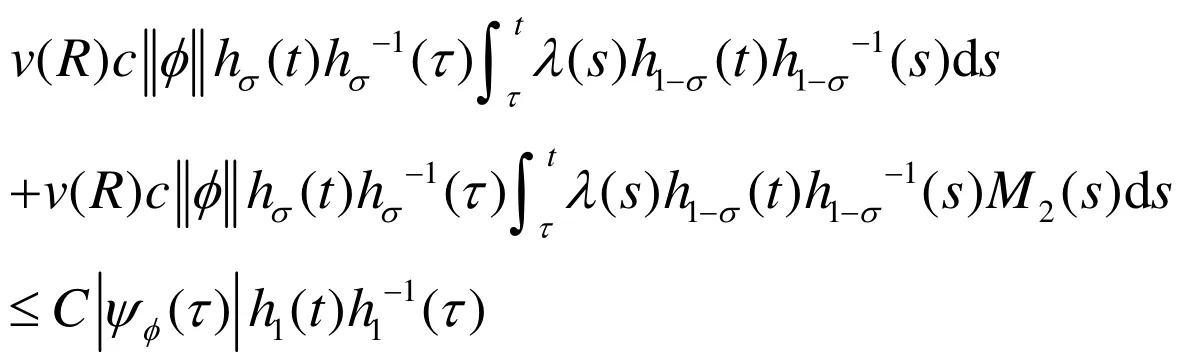
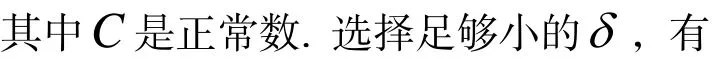
由（H3）可得，

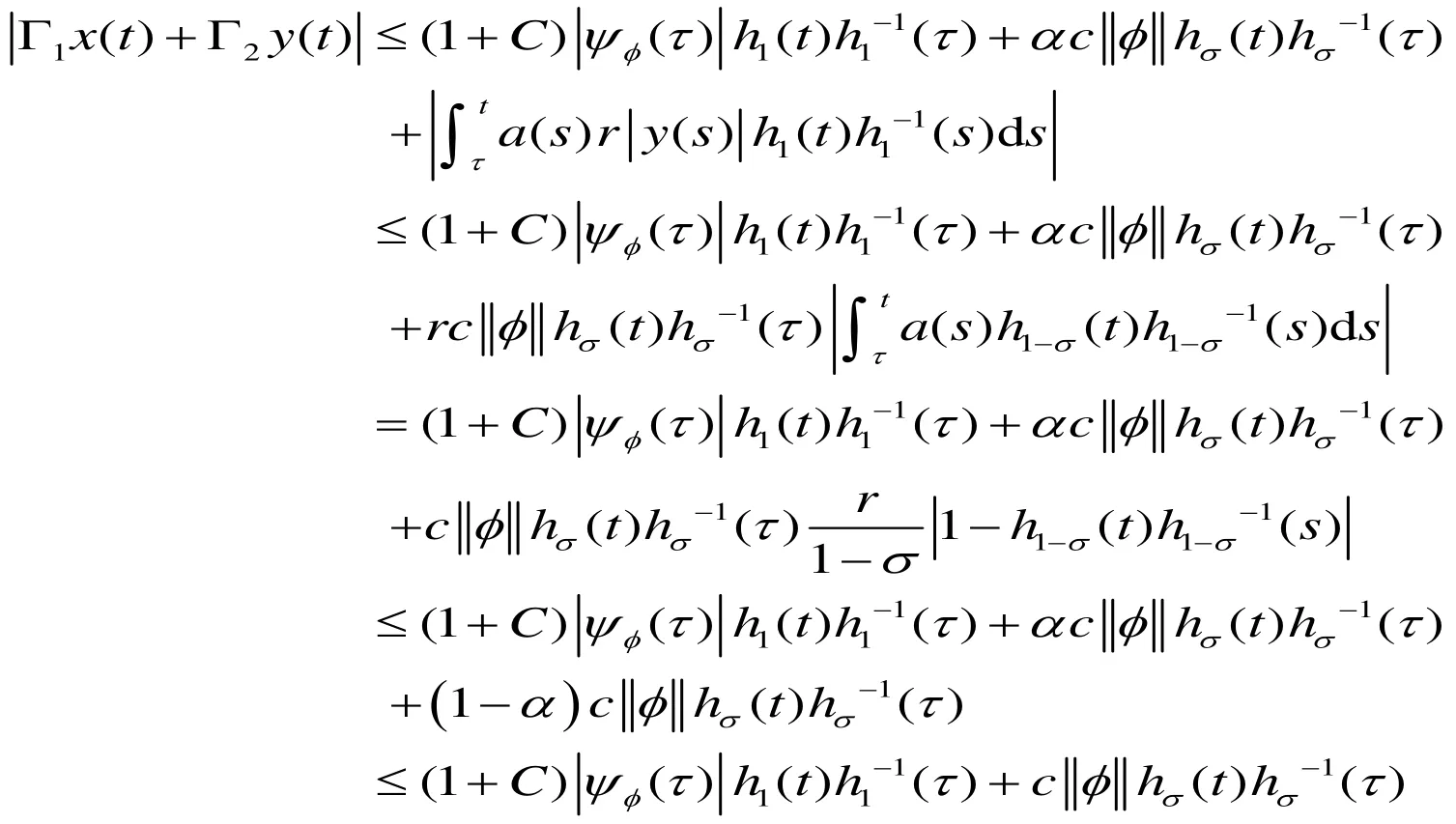
4 范例

成立，则（H1）,（H2）和（H3）成立.

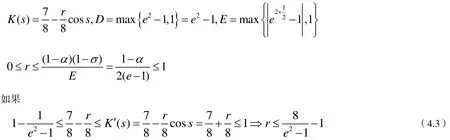
成立，则（3.10）成立.

如果

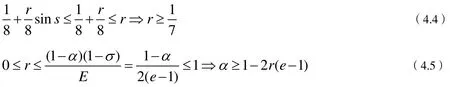
成立，则（3.11）成立.

由（4.4），（4.5）得

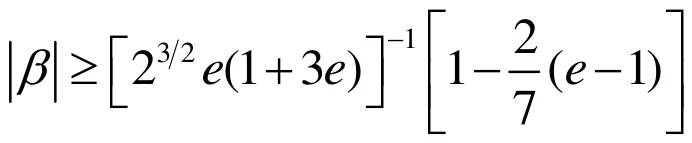
由（4.2），（4.8）得

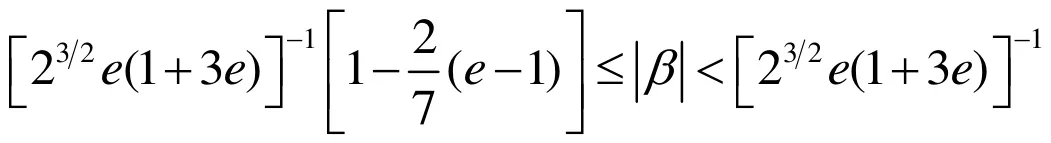
推论4.1 如果（4.1）中的

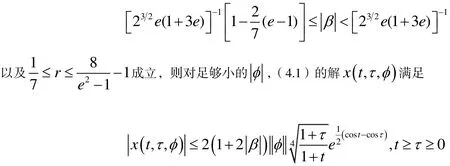
参考文献：

[1] BURTON T A.Liapunov functionals, fixed points, and stability by Krasnoselskii's theorem[J].Nonlinear Studies, 2002, 9(2):181-190.

[2] BURTON T A.Stability by fixed point theory for functional differential Equations[M].New York: Dover Publications, 2006.

[3] BURTON T A, FURUMOCHI T.Krasnoselskill's fixed points theorem and stability[J].Nonlinear Analysis Theory Methods and Applications, 2002, 4(49):445-454.

[4] PINTO M, SEPÚLVEDA D.H-asymptotic stability by fixed point in neutral nonlinear differential equations with delay[J].Nonlinear Analysis ,2011, 4(74),3926-3933.

[5] RAFFOUL Y N.Positive periodic solutions in neutral nonlinear differentral equations[J].J.Qual.Theory Diff.Equa 2007 16:1-10.

[6] YANKSON E.Existence of periodic solutions for totally nonlinear neutral differential equations with functional delay[J].Opuscula Mathematica, 2012 3(32):617-627.

[7] ZHANG B.Fixed point and stability in differential equations with variable delays[J].Nonlinear Analysis ,2005,5-7(63):233-242.

【责任编辑：吴跃新】

H-Asymptotic Stability by Fixed Point in Nonlinear Differential Equations with Delay

HUANG Minghui
（Department of Foundation Courses, Guangzhou Hua Xia Technical College, Guangzhou 510935, Guangdong, China）

In this article，we use a variant of Krasnoselskii's fixed point theorem to obtain h-asymptotic stability results about the zero solution of nonlinear neutral differential equations with functional delay.Our results generalize previous results due to Pinto and Sepulveda[4].We provide an example that illustrates our results.

h-asymptotic; large contraction; nonlinear

A

1671 - 5934 (2017)03 - 0024 - 11

2017 - 03 - 21

广东省自然科学基金 （2015A030310390）

作者简介：黄明辉(1988- ), 男, 广东从化人, 讲师, 硕士, 研究方向为微分动力系统, Email: 249596697@qq.com