“数形结合”思想在不等式问题中的运用

闫平继

(安徽省临泉第一中学，安徽 阜阳 236400)

“数形结合”思想在不等式问题中的运用

闫平继

(安徽省临泉第一中学，安徽 阜阳 236400)

著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休.”这段话精确地阐述了“数”与“形”之间相辅相成的关系.在江苏高考数学中，对于不等式问题的考查已经是不可或缺的一道题目了.而大多数不等式问题都会运用到“数形结合”的思想，这样不但可以使代数问题化繁为简，化难为易，化抽象为具体，而且发散了学生们的思维方式，提高了解题能力.

高中数学 不等式问题 数形结合

“数形结合”思想就是将复杂的代数问题转化为直观的几何问题.学生在求解不等式问题中，经常会遇到较为复杂的不等式，导致计算量特别大，步骤比较繁琐，最后对题目失去信心.这时候合理运用“数形结合”的思想，结合几何图形，反而会很直观的求解出答案，同时也提高了解题效率.

一、化数为形，以形助数

“化数为形，以形助数”，就是要用几何图形去解题，学生们在遇到看似特别复杂的不等式时，要会画出它的几何图形，会看不等式之间的关系，这就已经成功了一大半.用“形”来表达“数”，实现不等式之间的转换，以最快，最准确的速度求解出答案.

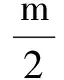
点拨 看似一道不等式问题，却结合了集合、方程和圆一起考察，所以解这道题的关键所在是“以形助数”，要会将求实数m的取值范围的问题转换为求直角坐标系中动直线与圆的交点的问题，从而在几何中找出问题的答案，“以形助数”更加清晰明了，准确快速！

二、寓数于形，构造函数

学生在解不等式的过程中，要发散思维，可以通过不等式的结构，构造相应的函数，然后利用“数形结合”的思想，在直角坐标系中将其表示出来，通过观察图象，求解出答案.

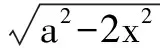
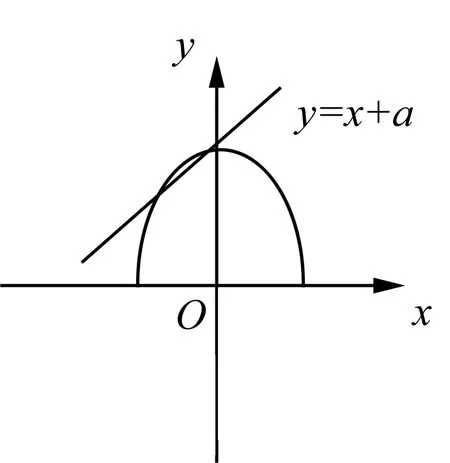
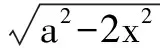
点拨 像这种比较抽象的不等式求解，如果运用常规的方法，既费时间还容易出错，学生们脑海里要一直装着函数，方程，以及圆的知识，学会灵活运用，此题就要用到构造函数的思想，再利用“数形结合”，观察函数图形，便能够快速准确的求解代数问题.给学生们做题也减少了不少麻烦，增强学生们的自信，因此，利用“数形结合”，穿插函数的思想也至关重要.

四、线性规划，数形结合

线性规划问题在江苏高考中经常作为填空题频繁出现，主要考查学生们直线的基础知识，经常用到“数学结合”的思想，将不等式组给出的条件转换为比较直观点的图象，先画出可行域，再利用图象，求解目标函数.

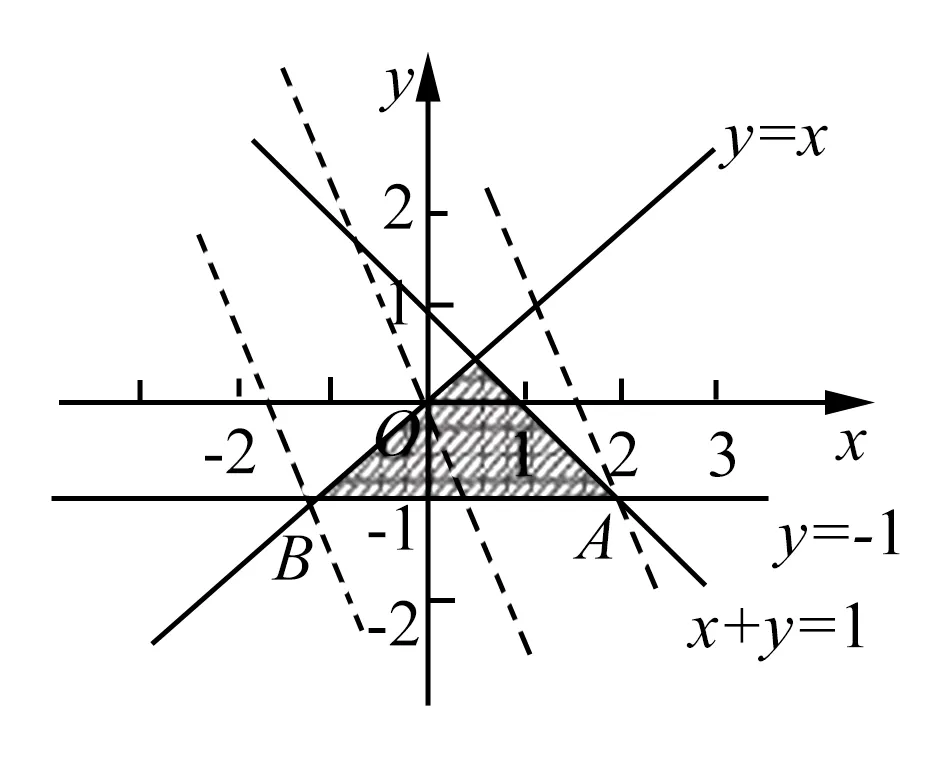
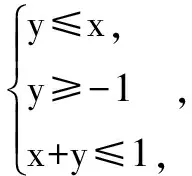
点拨 学生们要理清思路，在求线性规划问题时，要结合图形去看，画出可行域，标注好数值，仔细观察图形，审清题目，通过这个例题，可以认识到“数形结合”思想，给线性规划问题带来的好处，既简便又直观，更能够体现出“数形结合”思想的精髓所在！

通过在不等式问题中对“数形结合”思想的讲解，相信学生也收获了好多知识，解决了学生们在求解不等式问题时遇到了麻烦，“数形结合”思想的养成对于学习数学知识至关重要，可以帮助学生们减轻计算带来的压力，理清思路，更加直观地求解出答案，因此就需要老师在平时的授课中不断的引导，学生们努力的学习，架设好“数”与“形”之间的桥梁！

[1]汪金花.例谈数形结合思想在不等式证明中的应用[J].宿州教育学院学报,2001(11).

[2]宁智明.在不等式解法的教学中培养学生的数形结合思维能力[J].内蒙古教育(职教版),2014(9).

[责任编辑：杨惠民]

2017-05-01

闫平继(1982.10-)，男，安徽临泉人，中学一级教师,本科学历.从事数学教育和班主任工作.

G632

B

1008-0333(2017)19-0034-02