妙用向量的“积化和差”公式解题

江苏省常州市第二中学(213003) 王强

妙用向量的“积化和差”公式解题

江苏省常州市第二中学(213003) 王强

新修订的《江苏高中数学课程》提出,数学核心素养是数学课程目标的集中体现,是具有数学基本特征、适应个人终身发展和社会发展需要的必备品格与关键能力,是数学课程目标的集中体现.它是在数学学习的过程中逐步形成的.数学核心素养包括:数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析.数学运算是六大核心素养之一,是指在明晰运算对象的基础上,依据运算法则解决数学问题,具体体现在理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果.《向量》是近代数学中重要和基本的数学概念之一,它是沟通代数、几何与三角函数的一种工具.向量是数形结合的载体,具体地说,向量的几何表示、向量的三角形运算法则等都是从几何的角度对向量的研究,而向量的坐标表示、坐标运算就是用代数的方法来研究向量了.向量运算涉及坐标运算、基底运算和几何图形,学生常常难以选择合适的运算方法,无法从不同的视角,灵活探索运算方法.向量也是江苏高考的必考点,其中向量的数量积更是高考的C级考点,最近笔者借助几何图形的方法,得到了向量数量积的“积化和差”公式,笔者进一步发现在一些高考题和模考题中,合理地使用“积化和差”公式能起到“四两拨千斤”的效果,极大地减少运算量.本文就此谈一点自己的思考,恳请读者不吝赐教.

1.公式推导

结论:对于任意的两个向量

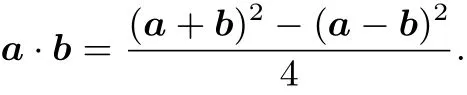
证明 因为

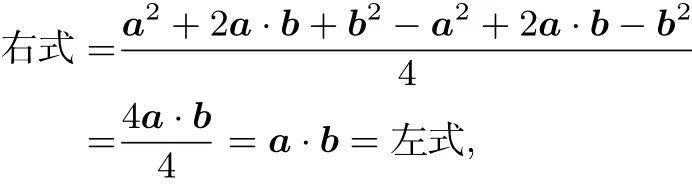
结论成立.

推论 在△ABC中,D是BC的中点,则有

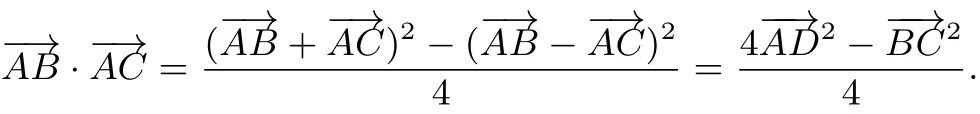
2.方法对比

例1(2016江苏高考第13题)如图1,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,=4,则的值是______.

图1

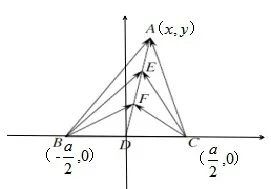
图2

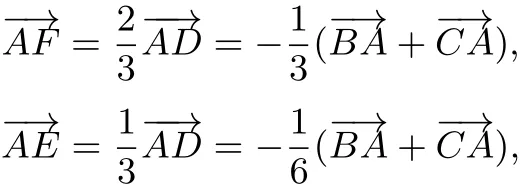
从而

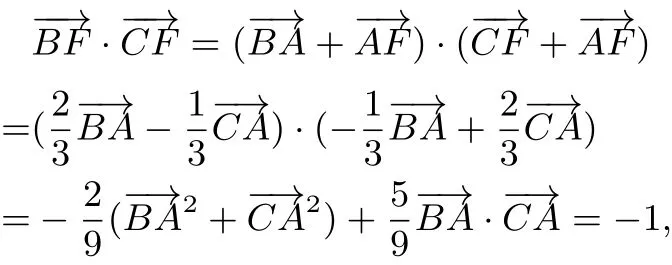
法三(积化和差公式)因为

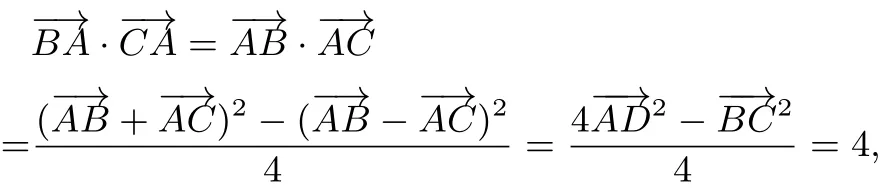
所以

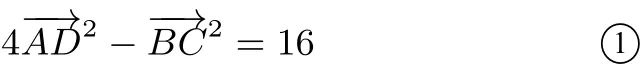
因为

又F是AD上的一个三等分点,所以

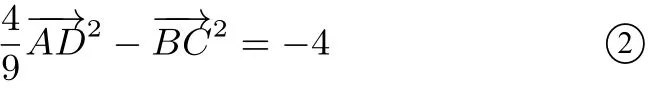
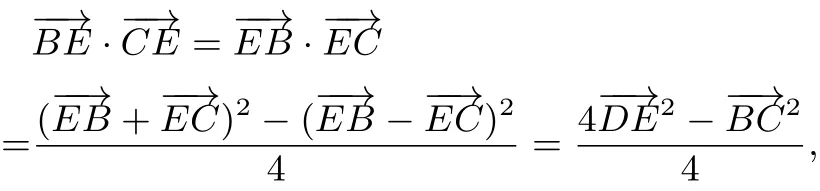
又E是AD上的一个三等分点,所以

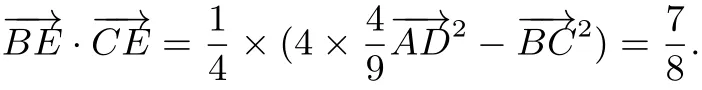
点评 求解平面向量的有关问题,通常有两种运算方向:一是通过建立直角坐标系,转化为向量的坐标运算来加以解决；二是选择两个不共线的向量作为基底,通过将所有的向量转化为基底的方法来加以处理.一般地,运用向量的坐标运算时可操作性强,而运用向量的基底时对思维的要求较高.利用向量数量积的“积化和差”公式解题为向量运算提供了另一个方向,尤其对于中线向量问题来说能起到“四两拨千斤”的效果,极大地减少运算量.

3.公式应用

江苏高考中,向量数量积是高考的C级考点,在各地模考卷中经常是以难题的形式出现.下面谈谈利用“积化和差”公式在解向量数量积问题中的应用.

图3

例2(2016南通二模第12题)如图 3,在同一平面内,点A位于两平行直线m,n的同侧,且A到m,n的距离分别为1,3.点B,C分别在m,n上,则的最大值是__.

解点B,C分别在m,n上,所以BC的最小值为直线m和直线n间的距离2,所以的最大值是

设A(x0,y0),则

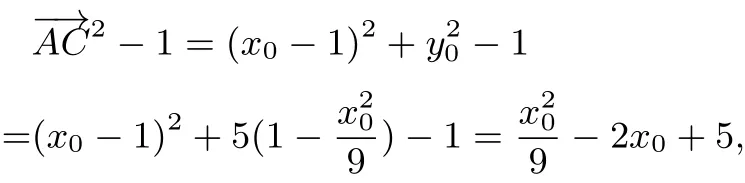
又因为x0∈[−3,3],由二次函数的对称性得,当x0=−3时,取最大值15.

例4 (2015南通三模第11题)如图 4,已知正方形ABCD的边长为2,点E为AB的中点.以A为圆心,AE为半径,作弧交AD于点F.若P为劣弧EF上的动点,则的最小值为____.

图4

解 取DC的中点为G,则

由圆的对称性知,当P为AG与劣弧EF的交点时,PG最小

例5(2014南京三模第12题)在Rt△ABC中,CA=CB=2,M,N是斜边AB上的两个动点,且则的取值范围为____.

解 设MN的中点为D,则

4.活学活用

读者可以尝试用“积化和差”公式解决以下两道问题,加强对公式的理解和运用能力.

练习1 如图,P为以AB为直径的圆O上任意一点,且OP = PC,若

图5

练习2已知在矩形ABCD中,AB=2BC,BC=a,长度为a的线段EF的端点分别在边BC和CD上,则的最大值为____.

答案练习1:12;练习2:4a2.

5.感受

著名教育家波利亚说过:“没有一道题是可以解决得十全十美的,总剩下些工作要做,经过充分的探讨与钻研,总会有点滴的发现,总能改进这个解答,而且在任何情况下,我们都能提高自己对这个解答的理解水平.”用“积化和差”公式解决平面向量数量积问题,可以将不好计算的数量积转化成好计算的线段长度,体现了转化和化归的数学思想方法.一句话说的好“生活不是缺少美,而是缺少发现美的眼睛”,数学解题也是这样.