利用图像解一类绝对值函数的最值问题

浙江省绍兴市柯桥区豫才中学(312000) 陈佳乐

利用图像解一类绝对值函数的最值问题

浙江省绍兴市柯桥区豫才中学(312000) 陈佳乐

近几年,在各地市及高考中考查关于绝对值的最值问题屡见不鲜.本篇以图像为载体,研究了一类形如f(x)=|g(x)+b|的最值问题,从我们常见的最值问题切入,由简到繁、由易到难、有抽象到直观、由特殊到一般地提出了解决这类问题的一般解法.

例1已知f(x)=|x−a|(a∈R).

(II)若存在x0∈[1,2],使得f(x)≥求满足条件的a的集合.

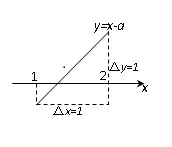
图1

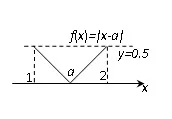
图2

解 显然只要满足fmax(x)≤即可,当然我们可以通过代数方法利用分段函数max{f(1),f(2)}≤来解决,本篇重点介绍图像法解题,代数法留给读者自行解决.

考虑函数y=x−a图象,如图1,因为 ∆x=∆y=1,考虑f(x)=|x−a|.绝对值对图像得变换即把x轴下方图像翻至上方,不难得出fmax(x)≥恒成立,当且仅当时(a为区间[1,2]的中点)如图2所示,fmax(x)=满足题意,所以

(2)只要满足fmax(x)≥即可,由图2不难得出恒成立,所以a∈R.

变式1已知f(x)=|x−a|(a∈R),若存在唯一的实数m,满足对任意的x∈[m,m+1],使得f(x)≤t恒成立,求t的最小值.

解 此题看似与例1不同,实则完全相同.考虑函数y=x−a图象如图1,因为∆x= ∆y=1,观察图2,由f(x)图像可得fmax(x)≥恒成立,不同之处在于此题是研究在区间[m,m+1]上的情况,但是不难得出所谓唯一的m=a−值得关注的是:因为所考虑的函数是一次函数,所以a为闭区间[m,m+1]的中点,所以t的最小值为

变式2 已知f(x)=|ax+b|(a∈R),若对任意的实数b,总存在x0∈[1,2],使得f(x0)≥,求a的取值范围.

解 即要满足fmax(x)≥因为∆y=|a|,考虑绝对值对图像得变换,所以fmax(x)或a≥1.

同样的,这里也总存在实数b平移至函数图象中A与B平齐,使得fmax(x)≥并且也不难得出此时的

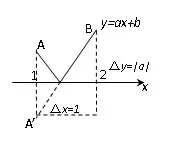
图3

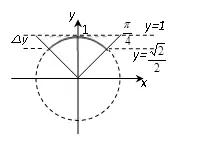
图4

例2已知f(x)=|sin(x+φ)+b|,若存在实数b,φ,满

所以在一般情况下∆y=ymax−ymin,由图得

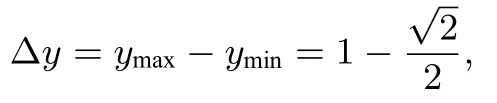
所以

变式 已知f(x)=|sin(x+φ)+b|,若存在唯一实数对(b,φ),满足对任意的使得f(x)≤ t恒成立,则t=____.

结论 一般地,已知f(x)=|g(x)+b|;

(I)若存在实数b,满足对任意的x∈[m,n],使得f(x)≤ t恒成立,则t的最小值=此时

(II)若存在唯一的实数b,满足对任意的x∈[m,n],使得 f(x)≤ t恒成立,则此时

(III)若对任意的实数b,总存在x0∈[m,n],使得f(x0)≥ t0,则t的最大值=此时

上述三种表述为等价表述.运用上述结论解题时,如已知晓的单调性的前提下,甚至都不要画图就可解决这类问题,以下是上述结论的应用.

练习1(自编)已知f(x)=|ax+1|(a∈R),若对任意的x∈[1,2],使得f(x)≤m恒成立,求m的最小值.

C.(−∞,1] D.(−∞,2]所以

练习3记f(x)=|lnx+ax+b|(a＞0)在区间[t,t+2](t＞0)上的最大值为Mt(a,b),若{b|Mt(a,b)≥ln2+a},则实数t的最大值是( )

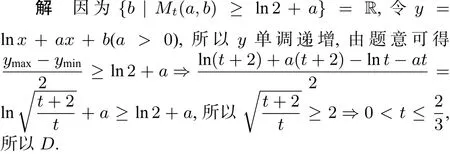
此结论还可以推广至一般有界函数的情况下,不是一定要在闭区间[m,n]上才成立,本篇就不再进一步展开了.不难发现利用图像法解这类问题实则考验的是学生对数学中“数”与“形”的理解以及学生运用“数形结合”这一数学思想的能力,培养了学生直观想象的数学核心素养.