“怎样解题”表在离散型随机变量问题中的运用

华南师范大学数学科学学院(510631) 郑育玲 卓健民

“怎样解题”表在离散型随机变量问题中的运用

华南师范大学数学科学学院(510631) 郑育玲 卓健民

波利亚“怎样解题”表集中体现其探索法与元认知思想,在函数、方程、立体几何、解析几何等方面的解题教学中应用广泛.目前关于离散型随机变量问题的解题研究并不多,这可能是因为概率问题具有的“随机性”特征与通常的函数、几何问题不同.特此设计离散型随机变量分布列的解题表(表1),在继承波利亚“怎样解题”表思路的同时,体现离散型随机变量问题的特殊性.本文将通过两个典型例子来说明“怎样解题”表在离散型随机变量问题中的运用.

表1 离散型随机变量分布列的解题表

回顾反思,构建知识迁移⋆你能检查你的答案吗?概率是非负数吗?分布列的概率之和是否等于1?⋆你可以换个角度看这个问题吗?能不能用别的方法导出这个结果?⋆如果改变了条件,你会解决这个问题的变式吗?能否把题目或这种方法解决其他问题?

例1.(2015福建)某银行规定,一张银行卡若在一天内出现3次密码尝试错误,该银行卡将被锁定.小王到该银行取钱时,发现自己忘记了银行卡的密码,但可以确认该银行卡的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直到该银行卡被锁定.求:(2)设当天小王用该银行卡尝试密码的次数为X,求X的分布列和数学期望.

弄清问题,确定随机变量

盯住目标!问题要求我们要求我们做什么?随机变量是什么?

引导学生把注意力集中到未知数上—要求当天小王用该银行卡尝试密码的次数的分布列和数学期望,随机变量X表示尝试密码的次数.

与随机变量相关的条件有哪些?随机变量是X可能取值是什么?你可以列出来吗?

寻找与未知数密切联系的已知条件— 与随机变量X相关的条件有:出现3次尝试错误银行卡就会被锁定,正确密码是常用的6个密码之一,不重复地随机选择一个进行尝试.因此,有可能尝试一次就正确,有可能需要尝试两次,最多尝试三次.对应随机变量X的取值为1,2,3.

拟定计划,探究概率分布

怎么求对应取值的概率?具体说说随机变量不同取值时代表什么意思?

组织问题特征,分析所有可能情形— “X=1”表示小王作出了第一次尝试并且正确;“X=2”表示小王第一次尝试错误,作出第二次尝试并且正确;“X=3”表示小王第一次和第二次尝试均错误,作出第三次尝试,而第三次尝试正确或者错误均有可能.

我们先考虑“X=1”时的概率,你能引入符号表示第一次尝试正确这一事件吗?

引入符号,具体分析每一情形— 记A表示“第一次尝试并且正确”的事件.

此时将随机变量取值为1的概率转化为求事件A的概率,那么事件的概率怎么求?你能想到基本事件的概率公式吗?

由古典概型的概率公式

A包含的基本事件的个数为1,而基本事件总数为6,因此P(A)=对应“X=1”时的概率是多少呢?

类似地,你能用符号表示“第二次尝试并且正确”的事件吗?此时“X=2”的概率怎么求?第三次呢?“X=3”的概率呢?

记B表示“小王第二次尝试并且正确”的事件,由概率公式

并且由题目条件“小王不重复地随机选取”知此时的基本事件总数为5,包含的基本事件数仍为1,则P(B)=依据互斥事件和独立事件的概率公式我们可以得到

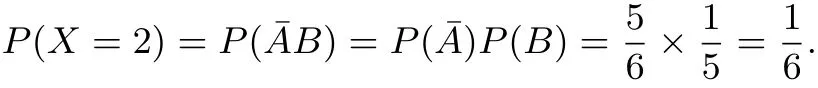
记C表示“小王第三次尝试并且正确”的事件,由概率公式

并且由题目条件“小王不重复地随机选取”知此时的基本事件总数为4,C包含的基本事件数仍为1,则P(C)=我们知道,不管第三次尝试是否成功,都不可能再进行下一次.依据互斥事件和独立事件的概率公式我们可以得到

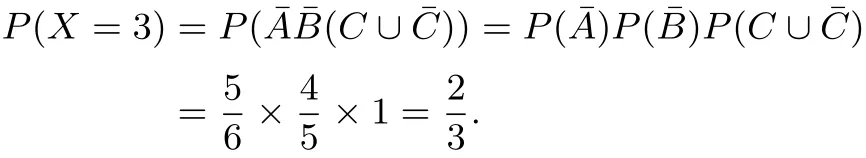
求出随机变量各取值对应的概率之后,根据公式便能求出随机变量的期望.

执行计划,落实解题步骤

现在可以把你的解题计划付诸实施了,你能清楚地看出每一步骤是正确的吗?

落实与检查每一步骤— 依题意得,X所有可能取值是1,2,3.

所以X的分布列为

X 1 2 3 P 1 1 2 6 6 3

所以

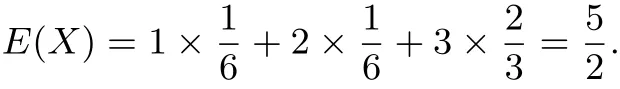
回顾反思,构建知识迁移

你能检验你的答案吗?每一步的推理是否合理的、有效的?计算是否正确?分布列的概率之和是否等于1?

学生基本上都能识别题目的背景实质上就是不放回的随机试验,即从6个基本事件中不放回地逐个抽取,直到抽到目标为止,随机变量X则表示的是抽取次数.与之相对的则是放回的随机试验,对于两者的区分是学生在学习过程中的薄弱之处,也是高考当中的热点.因此,在这里教师明确指出并正确引导学生进行区分与迁移是很有必要的.

例2. 为了解某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图.已知图中从左到右的前三个小组的频率之比为1:2:3,其中第2个小组的频数为4.

(1)求该校报考飞行员的总人数;

(2)若从该校报考飞行员的同学中任选3人,设X为表示体重超过60 kg的学生人数,求X的分布列和数学期望.根据频率分布直方图的知识,学生不难求得该校报考飞行员的总人数为16.

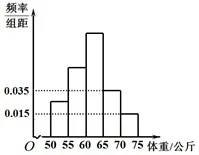
图1

下面将结合波利亚怎样解题的思想对第二问进行分析.

弄清问题,确定随机变量

问题要求我们做什么?随机变量是什么?

引导学生把注意力集中到未知数上— 求X的分布列和数学期望.是从该校报考飞行员的同学中任选3人,体重超过60 kg的学生人数.

与随机变量相关的条件是什么?随机变量的取值可以是多少?你可以列出来吗?

进一步了解问题的已知数和条件— 已知该校报考飞行员的总人数为16人,其中体重超过60kg的有10人,不超过60 kg的有6人.随机变量的取值可以为0,1,2,3.

拟定计划,探究概率分布

你想起一个求随机变量分布列的熟悉问题吗?在那里你是怎样解决的?

激活求离散型随机变量分布列的一般模式— 要求X的分布列,需要知道随机变量每一个取值所对应的概率.

随机变量为1是什么意思?你可以求出随机变量为1时的概率吗?这里有没有一些隐含的条件?

组织问题特征,分析特殊情形— 随机变量为1指的是从60名学生中选得的3名学生中,有1名体重超过60kg,其余2名体重不超过60 kg.其中,前1名学生来自体重超过60 kg的10人,后两名学生来自体重不超过60 kg的6人.容易联想到古典概型的计算公式,

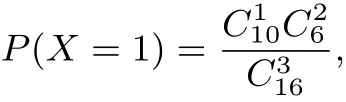
而16名学生任选3名隐含着古典概型等可能性与有限性的条件.

你可以求出随机变量为其它值时的概率吗?你是否能够想到一个熟悉的概率模型?

归纳一般情形,识别概率模型— 在这里学生也许已经能够发现超几何分布是本题背后的概率类型,但也有可能继续沿着上面的思路,分析随机变量为其它特殊值的情形,然后才注意到超几何分布的模型特征.无论是哪一种情况,它们都经历从特殊到一般的探索思路.这种分析问题的策略有助于充实问题的条件,促使产生解决问题的启发.

执行计划,落实解题步骤

现在可以把你的解题计划付诸实施了.你能清楚地看出每一步骤是正确的吗?落实与检查每一步骤— 为了真正掌握离散型随机变量分布列问题求解的一般方法,学生有必要自主落实与检查每一步骤.当学生满意地看出最终的思路—本题确实满足超几何分布的条件、随机变量的取值与实际相符、概率与期望公式运用正确,他们也不那么容易忘记.

回顾反思,构建知识迁移

你能检验你的答案吗?分布列的概率之和是否等于1?数学期望的计算结果是否合理?

如果改变了条件,你会解决这个问题的变式吗?

(2∗)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选3人,设X表示体重超过60 kg的学生人数,求X的分布列和数学期望.

变式明确要求“以这所学校的样本来估计总体数据”,其含义是用频率估计概率,即运用16人中每个人超过60 kg的频率代替全省每位学生体重超过60 kg的概率.原题从16人中任选3人可以看做复合试验,先在16人中任选1人,再从剩余的15人中选1人……每次试验的条件均不相同;而变式题是从全省报考飞行员的同学中(人数很多)抽取3人,考查体重超过60 kg的学生人数,随机试验之间是相互独立的且每次成功概率不变,因此满足二项分布的条件.

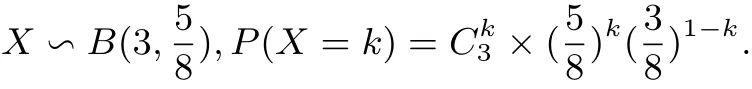
随机变量的分布列为:

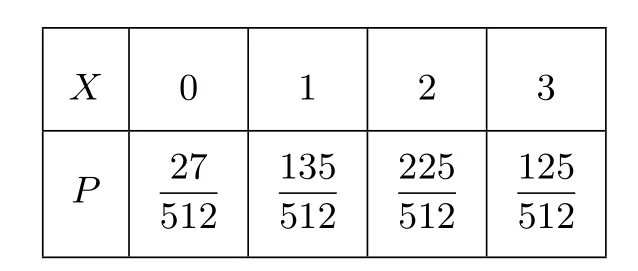
X 0 1 2 3 P 27 135 225 125 512 512 512 512

通过变式题,学生不仅能够注意到二项分布与超几何分布的差异,细心的学生还能够发现两者之间存在着某种联系— 两道题目的期望相同.这为学生进行数学探究、深化对离散型随机变量理解创造了一个良好的机会.

本文结合波利亚怎样解题的思想与离散型随机变量的问题特点,通过典型例子来谈离散型随机变量分布列的解题教学,对问题多次表征,引导学生识别概率模型,通过回顾反思,实现知识的正迁移.