一道三角形面积最值问题的探析

浙江奉化高级中学(315500) 柴骥宁

一道三角形面积最值问题的探析

浙江奉化高级中学(315500) 柴骥宁

2017年的南京一模的填空压轴出了个有关三角形面积最值的问题,如果翻阅近几年的江苏各地模考,能寻觅到2015年泰州就出现过与此相同的一个最值问题,虽是陈题,但其还是有值得研究的好题,一个题只要你留心和观察,方能看到不一样的成效,下面是笔者对于此题的一些见解和推广.

题目 (南京市、盐城市2017届高三年级第一次模拟考试第14题)在△ABC中,所对的边分别为a,b,c,若a2+b2+2c2=8,则△ABC面积的最大值为_____.

一.问题的解决

分析 显然这是一个有关三角形的面积最值问题,也就是三个关键点:三角形,面积,最值.首先,三角形就是涉及正余弦定理;其次,面积就是面积公式,一般涉及两种面积形式;最后,最值就是一般利用函数和不等式解决问题,有了这样的三个核心点,笔者有了下面的几种解法:

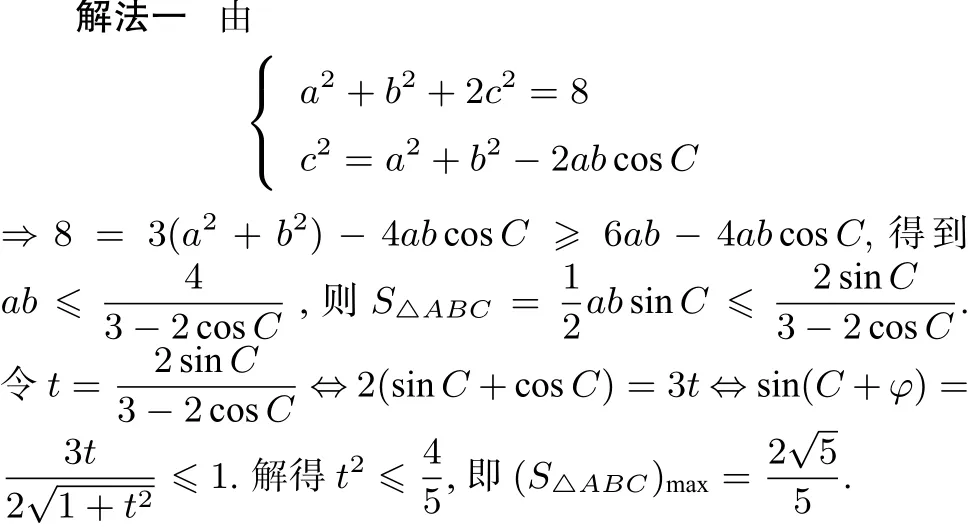
评注 此法主要是通过角的视角解决三角问题,通过简单的基本不等式和辅助角公式水到渠成地解决了此问题,当然其中的三角函数有界性是最终求得其最值的核心内核.

评注 此法是从角的视角解决三角形问题,边角互化其实是对解法一,二最好的阐述,当然法二还是通过简单的基本不等式放缩,通过转化成二次函数来解决这个问题,“最值问题函数解”这也是个常见而通俗的转化思想.

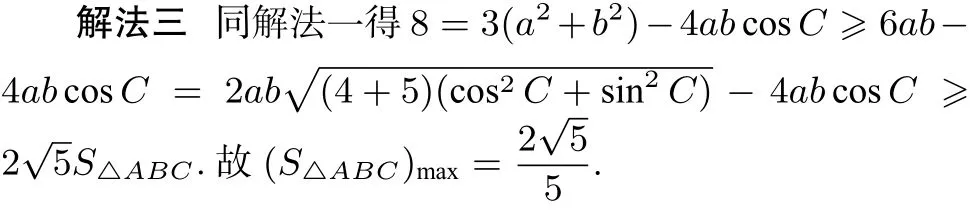
评注 此法类似于解法一,但又高于解法一,通过柯西不等式的放缩直接构造了三角形的面积公式,灵活但又简洁,这是体现数学简洁美的一个解法.

解法四 如图1,过C作CD⊥AB,垂足为D,则x+y=c.则

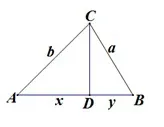
图1

评注 此法与上一解法异曲同工之妙,通过不等式的放缩直接构造了面积公式,只是一个从角的视角的面积公式,一个是低与高之间边的视角的面积公式,千丝万缕又面面相觑.

解法五 假设AB=c为定值,则以AB中点O建立平面直角坐标系,如图2,则不妨设C(x,y),其中a2+b2=8−2c2,则易得(x+

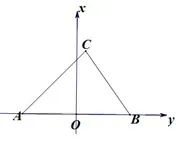
图2

评注 此法易感受到就如同是把解法四坐标化的诠释,其实几何问题代数化是解决几何问题的一大重要途径,此种方法有“重计算,轻思维”之嫌,也是学生在解决复杂几何问题时喜欢选择的方法,对于本题的此法,我们还发现(∗)式是一个圆方程,即揭示了一个圆的定义:平面内到两定点的线性平方和为常数的动点得轨迹即为圆.

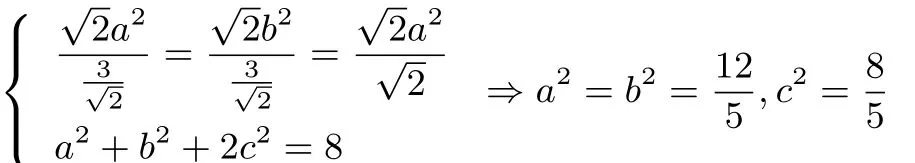
评注 此法利用一个面积与边之间的恒等式,结合四维的柯西不等式,轻巧而便捷地求得其面积的最大值,但这“简美”背后是数学知识“大道”的升华.

二.问题的推广

命题1 在△ABC中,所对的边分别为a,b,c,若xa2+yb2+zc2=t(其中 a,y,z,t均大于 0),则 (S△ABC)max=

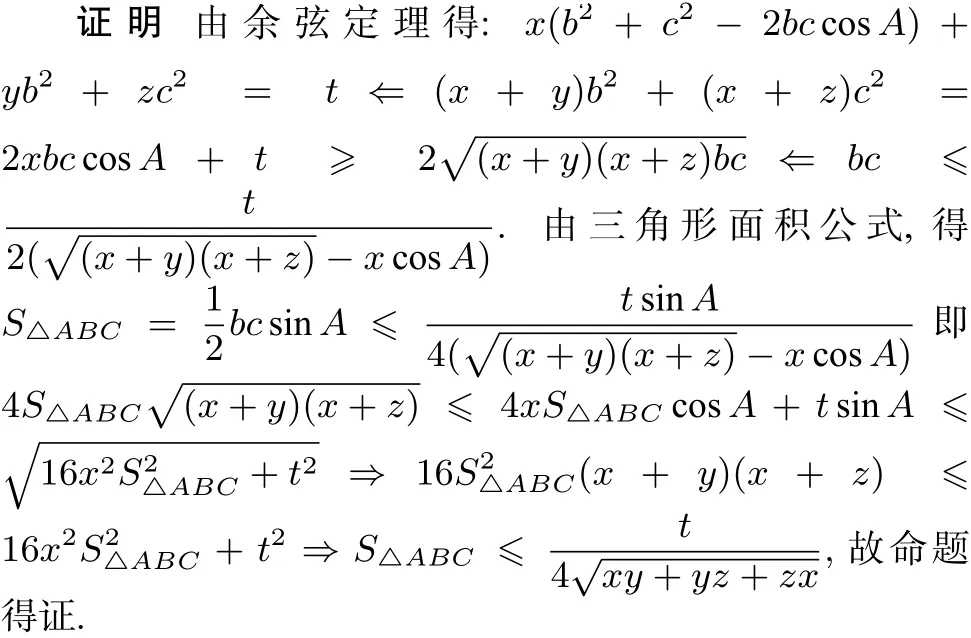
其实不然,上述命题是同解法一一致,自然而又适合通法同性的教学功能,其实上述的命题中,代回到结论中,可以表述成如下不等式命题:

命题2 在t=xa2+yb2+zc2中,所对的边分别为a,b,c若实数x,y,z＞0,则xa2+yb2+zc2≥

图3

证明 如图3,过A作AD ⊥ BC,垂足为D.设AD=k,BD=m,CD=n.则a2=(m+n)2,b2=k2+n2,c2=k2+m2,4S△ABC=2k(m+n).故只需证x(m+n)2+y(k2+n2)+z(k2+m2)≥2k(m+整理得(y+z)k2+x(m+n)2+yn2+故只需证故只需证

即证(y+z)[x(m+n)2+yn2+zm2]≥(m+n)2(xy+yz+zx).即证y(y+z)n2+z(y+z)m2≥yz(m+n)2⇔y2n2+z2m2≥2yzmn⇔(yn−zm)2≥0,故命题得证.

由(2)式不难发现,这个不等式要成立,只需

因此可以推广到如下的

命题3在△ABC中,A,B,C所对的边分别为a,b,c,若实数x+y+z＞0,xy+yz+zx＞0,则xa2+yb2+zc2≥

评注 注意到命题3,当x=y=z=1时,就是1919年Weitezenbock提出的关于三角形的著名不等式:,当且仅当△ABC为等边三角形等号成立.此题也许就是这个不等式背景的命题效果吧.

三.思维的启迪

通过对一道模考题的简单探析,能更好地把握住数学知识的整体性和统一性,能更好地感受到解题而非就题论题,作为数学教师应该站在数学知识层面去解题,让一个题真正焕发出它的生命力,这样才能真正体现出一个题目的教学功能性.通过对一个题目的细细品读和斟酌再三,能有效地提升教师的自身思维能力,作为数学教师应该是学生思维的领航者和引导者,只有数学教师自己能在题里看到一片天,才能使学生在天空中看到繁星.