利用不等式解方程

广东省佛山市罗定邦中学(528300) 龙宇

利用不等式解方程

广东省佛山市罗定邦中学(528300) 龙宇

在一般的解方程问题中,方程的个数与未知量的个数相同.当方程的个数小于未知量的个数时,方程可能无解,也可能有无数个解.但在某些特定的条件下,依然有唯一解.不过一般需要借助不等式,利用取“=”条件求解.本文以如下几个习题为例,向读者展示一下相关的解题思路.

1.利用不等式解方程的思想方法

已知方程f(x)=g(y).分别求两个函数的值域,若有fmin(x)≥gmax(y)或fmax(x)≤gmin(y).则说明方程两边同时取到最值.利用取“=”条件求解对应的未知量.

2.三角函数与解三角形

例1. 若sinαsinβ=1,求cos(α−β)的值.

分析 本题中有两个未知角,只有一个条件.结合三角函数的范围以及方程右侧的1,根据不等式的取“=”条件,获取更多的信息.

解 由 sinαsinβ = 1,可得: sinαsinβ ＞ 0,即sinα,sinβ同号.

设sinα＞0,sinβ＞0,由0＜sinα≤1,0＜sinβ≤1,得:0＜sinα·sinβ≤1.

由 sinαsinβ=1可知上面的 “=”均成立.即可知sinα =1,sinβ=1,由此可得:cosα =0,cosβ=0.所以cos(α−β)=cosαcosβ+sinαsinβ =1.

总结 本题利用均值不等式求解,而三角函数本身就有范围的限制.所以要特别注意“=”成立的条件.

例3.已知在△ABC中,角A,B,C所对的边为a,b,c,且有2sin2B+3sin2C=2sinAsinB sinC+sin2A,求角A的值.

解析 利用正弦定理,题干条件可转化为:2b2+3c2=

总结 本题利用了基本不等式及三角函数的值域

例4. (2010北大保送生考试)已知f(x)=ax+sinx表示的图像上有两条切线互相垂直,求a的值.

分析 f′(x)=a+cosx,如果f(x)的图像上有两条切线互相垂直.一定存在x1,x2使得f′(x1)f′(x2)= −1,即有(a+cosx1)(a+cosx2)=−1.表达式中未知量较多,且涉及余弦,直接求解困难.接下来,我们考虑一下它的范围.

解 不妨设cosx1≤cosx2,因为(a+cosx1)(a+cosx2)＜0,即有a+cosx1＜0,a+cosx2＞0.根据余弦函数的有界性,显然有:a+cosx1≥a−1,a+cosx2≤a+1.所以−1=(a+cosx1)(a+cosx2)≥(a−1)(a+1)≥−1.由此可知,上面所有不等式中的“=”均成立.所以a=0.

3.与指数或对数有关的超越方程

例5.(2015年全国高中数学联赛河南省预赛第4题)已知实数x,y满足:2x=ln(x+y−1)+ln(x−y−1)+4,求2015x2+2016y3的值.

分析 本题所给方程含有两个未知数,直接求解未知量非常困难.一般的思维在于将所求或题干条件视为整体求解.而本题涉及到对数、三次方、平方,整体思想也失效了.反思本题,题干的难点在于对数,借助常用不等式lnx≤x−1,将其放缩修改.

解 2x=ln(x+y−1)+ln(x−y−1)+4≤

x+y−1−1+x−y−1−1+4=2x观察上式可得,上式中的“=”成立.所以

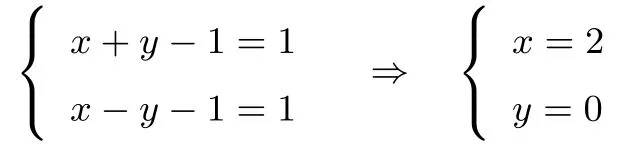
所以2015x2+2016y3=8060.

总结 为了便于放缩对数与指数函数,建议读者记忆一些常用结论.如:≤lnx≤x−1,当且仅当x=1时成立;ex≥x+1,当且仅当x=0时成立;ex＞lnx+2等.

分析 移项构造函数求解.

对于(1)式,左边的最大值=右边的最小值.所以两边同时取到最值.对应的x=2,所以的值为8.

分析 仿照上例,将上方程分离变量,分别求其值域.

4.利用方程解不等式

例7.已知函数f(x)=2lnx+x2+x,若正实数x1,x2满足f(x1)+f(x2)=4,求证x1+x2≥2.

解f(x1)+f(x2)=2lnx1+x21+x1+2lnx2+x22+x2=4.重新组合后可得:(x1+x2)2+(x1+x2)−4=2x1x2−2ln(x1x2)构造函数h(x)=2x−2lnx,易求得h(x)∈[2,+∞).所以(x1+x2)2+(x1+x2)−4≥ 2.令x1+x2=t,所以t2+t−6≥0,即可得t≤−3或t≥2.因为x1,x2是正实数,所以t≥2.

总结 本题的解法在本质上是构造函数h(x).为了保证等式成立,方程的左边的每个取值属于h(x)的值域,由此可得方程左边的基本范围,据此求得最终的结论.

5.练习

1. 若实数x,y满足2x−3≤ln(x+y+1)+ln(x+y−2),求xy的值.

提示:ln(x+y+1)≤x+y,ln(x+y−2)≤x−y−3.