例谈数学解题教学的“三法”观

陕西师范大学数学与信息科学学院(720000) 刘再平

陕西省镇巴中学(723600) 罗新兵

例谈数学解题教学的“三法”观

陕西师范大学数学与信息科学学院(720000) 刘再平

陕西省镇巴中学(723600) 罗新兵

解题教学是中学数学教学的核心环节之一,掌握数学就意味着要善于解题,从某种程度上来说,中学数学教学的首要任务就是加强有效的解题训练.而如今,解题在众多专业数学期刊和课堂上呈现出鲜明的一题多解态势,有的问题甚至给出了几十种解法之多,其中不凡一些极为诡异的解法,让人叹为观止、佩服不已!然而在佩服的同时笔者心生疑虑:如此多的解法都有必要铺天盖网的呈现给学生吗?盲目的一题多解对学生数学思维的激发与解题能力的提高真的有很大帮助吗?面对一题多解我们又该如何取舍呢?下文,笔者根据自身多年的解题教学经验,结合具体实例谈谈关于解题教学中的“通法、适用方法、巧法”的一些拙见.

解题教学中的“三法”:

通法 是处理某一类问题的常规方法,也是运用基本知识与基本技能直接就可以达到问题解决的方法,更是解题初学者最容易想到的方法.因此通法的教学是夯实基础知识、形成基本技能与提高解题能力的核心环节.通法对于多数学生来说容易掌握,但通法有时比较繁琐,不一定是最简单与最适用的方法.

适用方法 是相对比较简洁,利于学生操作,用时较少,效率比较高,但获得难度往往比通法大的方法.适用方法立足于通法,又高于通法,学生最好在掌握“双基”与通法之后,才展开适用方法的解题教学.适用方法是学生参与高考等解题活动的最理想方法.

巧法 是最为简洁,效率最高,能充分展示数学奇异美,然而又最难掌握的方法.巧法的获得往往不仅需要学生具备较高的数学素养,而且还要一定的创新思维.适当的渗透巧法对激发学生的数学学习兴趣、开拓学生数学思维有一定的帮助,然而过度的展开巧法教学,特别是在没有掌握通法和适用方法时就冒然呈现巧法,反而会大大降低解题教学的有效性,不仅不利于学生对基础知识与基本技能的理解,而且还有违课堂教学面向全体性的原则.

说明

1.某些问题的通法、适用方法与巧法可能不止一种,教师应根据学生已有的数学知识储备与实际数学水平合理渗透.

2.数学解题的实质是发生数学,而不仅仅是“规则的简单重复”或“技巧的生硬执行”,教师在解题教学中,不论是对通法、适用方法还是巧法的教学,都应该充分展示解题过程和暴露解题思维.

3.教师在展开对通法、适用方法与巧法的教学时,面对一题多解应该积极的向学生渗透多解归一的思想,以优化学生的解题思维,展示数学问题多解的辩证统一美.

(1)求椭圆的方程;

(2)求动点C的轨迹E的方程;

(3)设直线AC(C点不同于A,B)与直线x=2交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.

图1

分析 此道圆锥曲线试题的前两小问较为简单,其答案:(1)椭圆方程为(2)轨迹E的方程为x2+y2=4.第(3)问将圆锥曲线、圆、直线综合,稍有难度.然而,考虑到要证圆与直线相切,首先就会想到只需证明圆心到直线的距离等于半径,于是获得通法;若从向量视角出发,即证可以得到其适用证法;解析几何与平面几何联系紧密,若立足于平面几何,不难得到此题的平面几何证明巧法.

通法 设点C(m,n),点R(2,t),由题设,A,C,R三点共线,所以平行.

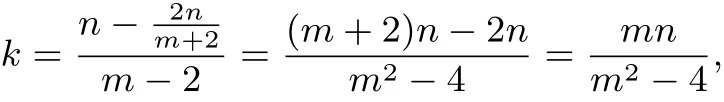
而m2+n2=4,即m2−4=−n2,所以所以直线CD的方程为

化简得 mx+ny−4=0.则圆心O到直线CD的距离

图2

故直线 CD与曲线E相切.

巧法 在图2中,连结OC、BC,则∠ACB=90◦,由题D为线段RB的中点,所以CD=RD,即∠R=∠DCR.因为∠R+∠BAR=90◦,即 ∠DCR+∠BAR=90◦.又OA=OC,所以 ∠BAR= ∠OCA,则 ∠DCR+ ∠OCA=90◦,即∠OCD=90◦.故直线CD与曲线E相切.

例2.(2014年陕西理科压轴题)设函数f(x)=ln(x+1),g(x)=xf′(x),x ≥ 0,其中 f′(x)是 f(x)的导函数.

(I)g1(x)=g(x),gn+1(x)=g(gn(x)),n∈Z+,求gn(x)的表达式;

(II)若f(x)≥ag(x)恒成立,求实数a的取值范围;

(III)设n ∈ N∗,比较g(1)+g(2)+···+g(n)与n−f(n)的大小,并加以证明.

分析 此题属于导数综合性压轴题,综合了函数、恒成立、不等式等重要考点考察学生分析问题、解决问题的能力与灵活运用分类讨论、数形结合等数学思想方法的技能.具体来说,第(I)、(II)问较为简单,第(III)问本质是证明数列和不等式”是真正的压轴点,证明时顺着命题者的意图,结合第(II)问结论,可以直接获得其解决通法;观察要证不等式的结构特点,联系到数学归纳法的适用范畴,于是得到其适用方法数学归纳法;挖掘此题的高等数学背景,结合定积分等相关知识,可以得到其巧法.

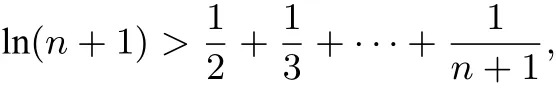
故得证.

即此时成立.故对一切n∈N∗结论都成立.

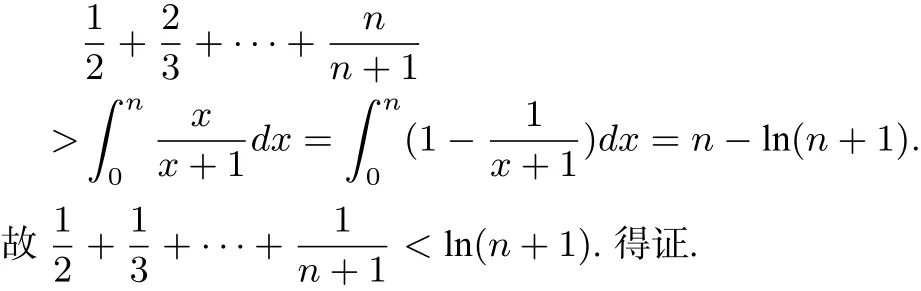
图3

例3.(《数学通报》2146征解题)若 n ∈ N∗,证明:

分析 此题是一道双边不等式问题,无疑放缩法是证明很多不等式的通法,该题也不例外;观察要证不等式的结构特点,联系到数学归纳法的适用范畴:常用于证明与正整数n有关的恒等式或不等式,于是得到其适用方法数学归纳法;分析不等式主体的各个因式分子与分母的特点,通过奇偶变换构造对偶式,再结合“糖水不等式”可以获得证明原不等式的构造巧法.

通法 要证原不等式,先证明如下一个简单的双边不等式:

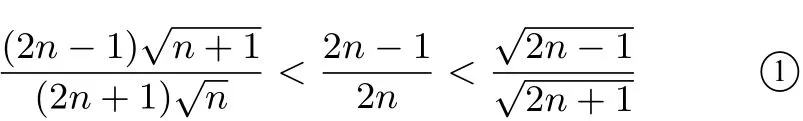
要证①式的左边,即证:即①式左边得证.

要证①式的右边,即证:

即①式右边得证.

由①式,

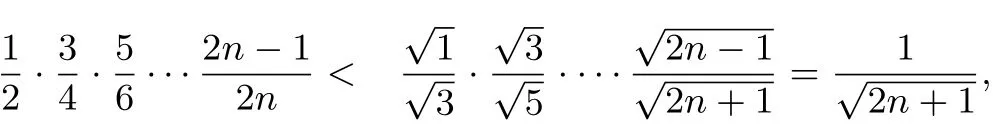
综上所述,原不等式得证.

成立,下面证明当n=k+1时的情况:

由假设得

另一方面,

所以,n=k+1时不等式也成立.综上所述,对n∈N∗原不等式成立.不等式左边得证.综上所述,原不等式得证.

关于解题方法,中科院院士、著名数学教育家张景中教授提出了经典的解题“中巧说”,即大巧法无定法,要靠个人领悟,难以言传,小巧一题一法,对于数学解题教学而言,则希望用一个方法解决一类题目,循序渐进的学习有章可循的解题通法.所以,在解题教学中我们首要的任务是夯实通性通法,然而通法往往是基于教材的基本方法,这些方法不一定简洁,还可能较为繁琐,为了缩短解题长度,提高解题效率,我们有必要渗透一些适用的方法,以提高学生的解题能力.章建跃先生认为解题教学主要有四大目的:“加深理解和掌握双基;培养和发展能力;查漏补缺;培养学习习惯,学会思考.”当这四个目的达到后,我们可以考虑介绍一些巧法,以激发学生数学学习兴趣,开拓学生眼界,促进学生数学思维的发展,更重要的是还能展示数学的奇异美,让学生获得数学美的享受.

最后,不论教师在展开通法、适用方法,还是巧法的解题教学时,都应该避免解题方法来的从天而降,务必要充分展示解题过程和暴露解题思维.因为,罗增儒教授对此多次提及:“分析典型题的解题过程,暴露数学解题思维是学会解题的有效途径.至少在没有找到更好的途径之前,这是一个无以替代的好主意.”

[1]罗增儒.数学解题学引论(第二版)[M].西安:陕西师范大学出版社,2008.9.

[2]刘再平.2014年陕西理科压轴题的另证与延伸[J].数学教学,2015(3):39–40.