波纹管-黏滞流体隔振器特性与实验

谢溪凌，陈燕毫，刁建超，张志谊

（1.上海交通大学 振动、冲击、噪声研究所，上海 200240；2.上海交通大学 机械系统与振动国家重点实验室，上海 200240）

波纹管-黏滞流体隔振器特性与实验

谢溪凌1,2，陈燕毫1,2，刁建超1,2，张志谊1,2

（1.上海交通大学 振动、冲击、噪声研究所，上海 200240；2.上海交通大学 机械系统与振动国家重点实验室，上海 200240）

针对振动敏感型电子器件的振动隔离问题，研究一种行程较大、动力放大因子较小、高频衰减率较高的隔振器。首先提出采用焊接波纹管和黏滞流体的两参数隔振器，其高频段衰减率约为-30 dB/dec，共振放大因子约为6 dB，然后通过力学建模给出提高隔振效率的三参数隔振器参数，通过串联弹簧和增大阻尼，进一步降低共振放大因子，同时改善高频区衰减效果。实验结果表明，三参数隔振器的放大因子小于5 dB，高频段衰减率约为-52 dB/dec；在0～500 Hz内，隔振后的加速度RMS值下降90%以上。

振动与波；振动隔离；焊接波纹管；黏性流体阻尼；三参数模型

高敏感器件的振动隔离是振动工程中的一类重要问题。随着目前各类数据传输基站的建立，加之信号传输模块对振动的高敏感性，振动控制更具迫切性和挑战性[1–3]，因此研究高性能被动隔振器具有重要意义。

隔振器的刚度和阻尼是决定隔振性能的两个重要参数。采用黏性流体介质产生阻尼已得到广泛应用。流体阻尼通过黏性流体流动过程中的内摩擦消耗能量[4]，是一种粘性阻尼，阻尼力范围很宽，且结构上易于实现。对于弹性元件，一般采用金属材料或其它复合材料，如螺旋弹簧、碟形弹簧、波纹管和橡胶等。此外，气体和流体也具有一定的刚度，也可作为弹性元件[5]。螺旋弹簧线性度好，易于设计与安装，而金属波纹管既可作为气、液体弹簧的承载件，又可提供刚度。焊接波纹管，作为金属波纹管的一种，是由多个环状膜片沿其内外边缘交替焊接而成的带横向波纹的管状壳体，相比于成型波纹管，能产生较大的位移，体积补偿能力大，并且在外压作用下能承受较大的过载[6]。

刚度和黏性阻尼并联的隔振器有明显不足之处，即隔振器阻尼可抑制共振峰，但也导致高频隔振性能下降。通常在被动隔振中，通过增加隔振级数来提高隔振性能，双层隔振最为常用[7]。

对于流体阻尼隔振器和三参数隔振器，国内外已有一些研究。该类隔振器在航天领域的应用以Hubble天文望远镜动量轮隔振所采用的粘滞流体隔振器为代表[8–9]。近年来，结合多作动器隔振平台，何玲对影响流体阻尼器隔振性能的非线性因素进行深入的理论分析和实验研究[5]。Gao利用成型波纹管作为弹性元件，对一种液固混合介质隔振器的动力学特性展开分析[10–11]。针对黏性流体微振动隔振器，Wang研究了阻尼产生机理及刚度特性，建立了一种等效三参数理论分析模型[12]。Wang在三参数隔振原理与参数分析的基础上，给出了一种波纹管式流体隔振器设计和三参数隔振系统的设计方法[7]。Lee研制一种采用波纹管和黏性流体构成的主被动隔振器，并研究了其在温度变化下的隔振性能[13–14]。Chen研制一种以成型波纹管为弹性元件的流体隔振器[15]。

文中研究一种以焊接波纹管作为弹性元件、由黏性流体产生阻尼的隔振器，通过分析与实验测试确定其参数和隔振效果，为高敏感有效载荷提供一种行程较大、动力放大因子较小、高频衰减率较高的隔振方案。

1 隔振器结构

设计要求：单个隔振器工作空间为50 mm×50 mm×80 mm，四个并联工作，负载3.5 kg，隔振系统共振频率小于20 Hz，行程大于3 mm，动力放大因子小于5 dB，高频衰减率大于-40 dB/dec。

设计方案：隔振器结构如图1所示，主要由连接端盖、上法兰、焊接波纹管A、刚性壳体、阻尼孔、下法兰、焊接波纹管B以及底座构成。该隔振器利用焊接波纹管作为弹性元件和流体容器，当隔振器上端受力时，焊接波纹管A发生轴向变形，使上腔体中黏性流体通过阻尼孔流入下腔体，引起焊接波纹管B发生轴向变形，通过黏性流体在上下腔体中往复流动，从而产生阻尼效果，阻尼可通过阻尼孔大小进行调节。此外，隔振器在工作时上、下腔体中的焊接波纹管均处于压缩状态，使焊接波纹管在工作时保持较好线性刚度。隔振器最大压缩量可达焊接波纹管自由长的60%。

图1 隔振器结构示意图

所采用焊接波纹管尺寸均为外径40 mm、内径20 mm、高度12 mm。焊接波纹管刚度可由经验公式大致算出[6]，此外，考虑到波纹管注入流体后的动刚度变大，而且会随着阻尼孔径大小而变化[5]，为使隔振器共振频率较低，设计时选择较小的焊接波纹管刚度，此处焊接波纹管刚度为800 N/m，其中每层波纹厚度仅为0.063 mm。

对于黏性流体，选用稳定性较高的350cSt二甲基硅油，密度为980 kg/m3，350号，即动力黏度标准在25℃时为350 mm2/s。与普通液压油相比，二甲基硅油黏度大，且其黏度随温度的变化要比液压油小很多[16–17]。黏性流体同时影响着隔振器的刚度和阻尼，在计算阻尼时，可考虑流体流经阻尼孔的压力损失和沿程损失，再等效为线性阻尼，从而计算出所需阻尼孔的直径和长度[5]。

2 隔振特性

2.1 隔振特性测试与两参数模型

进行隔振器设计与分析时，通常将其等效成质量-弹簧-阻尼系统[18]，通过对该系统进行分析，为隔振器的结构参数整定提供理论依据。将隔振器等效为图2所示的单自由度两参数模型，其中Ma为负载质量，Ka为系统刚度，Ca为系统阻尼，x0和x1分别为基础位移和响应位移。

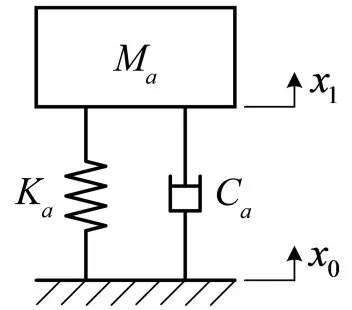
图2 单自由度两参数模型

两参数系统的运动微分方程可表示为

由上式可得到x1对x0的传递函数为

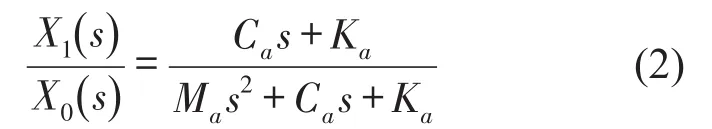
隔振器实物如图3所示。

图3 隔振器实物图

对两参数隔振器的隔振效果进行测试，测试系统包括：由四个隔振器组成的隔振平台（见图4）、振动台、加速度传感器（ICP）、数据采集与分析仪（LMS SCADAS）等，测试原理框图如图5所示。将隔振平台固定于振动台面上，加上负载质量（3.5 kg），通过外接白噪声激励信号，使振动台产生振动，以振动台面的振动加速度作为参考，测量隔振平台振动传递特性和隔振效果。

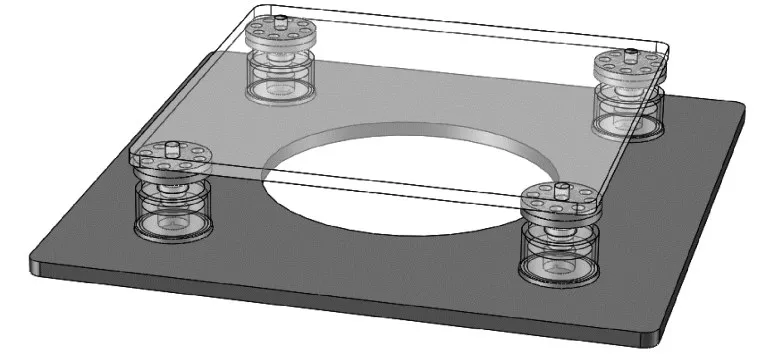
图4 四个隔振器组成的隔振平台

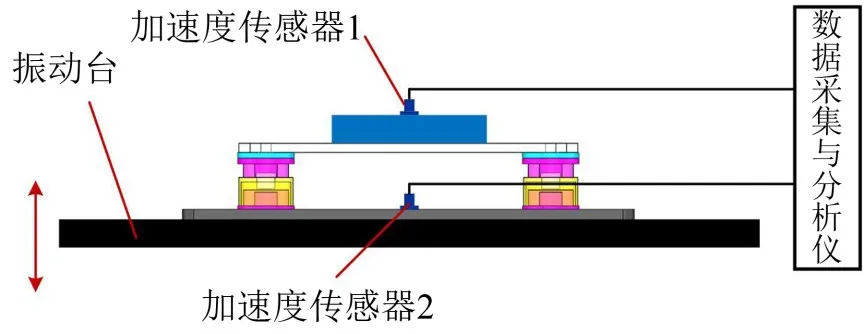
图5 隔振器测试原理框图

通过振动台施加垂向基础激励，测试和分析频带为0～250 Hz，测得隔振器的频响曲线，并将其与理论模型传递函数曲线进行对比，如图6所示。

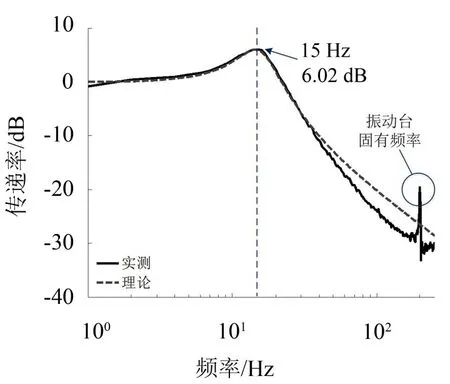
图6 两参数模型与实测频响曲线对比

由图6可以看出，频响曲线的低频段幅值在0 dB左右，隔振器共振频率在15 Hz左右，共振峰值约6 dB，表明共振放大因子约为2，隔振器具有较大的阻尼；曲线在22 Hz处传递率为0 dB，在160 Hz处传递率为-28 dB，经计算可得曲线在22 Hz～160 Hz频段内的衰减率为

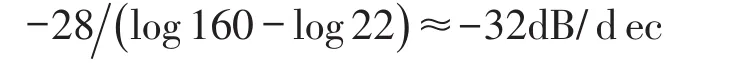
图中200 Hz的频率为振动台面固有频率。隔振器的实测传递曲线与两参数模型传递曲线在数值和趋势上吻合，具有较好的衰减特性。但是该隔振器高频衰减率还不够大。针对这个问题，考虑将两参数系统与一个弹簧串联，使之成为三参数系统，以增大高频衰减效果。

2.2 三参数模型

在两参数模型基础上，串联一个刚度参数，如图7所示，其中Mb为引入的附加质量，Kb为串联刚度，x2为附加质量的位移，其余参数与前述相同。

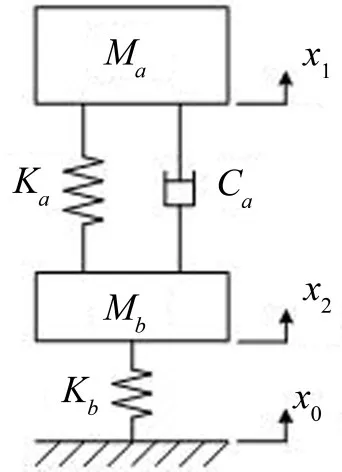
图7 两自由度三参数模型

三参数系统的运动微分方程可表示为

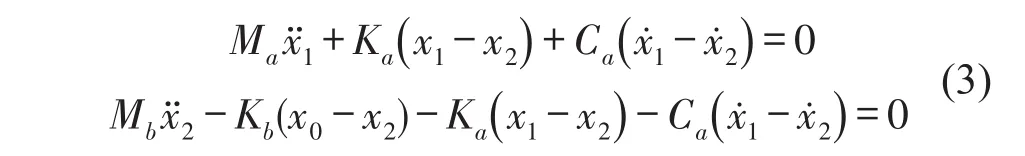
由上式可得到x1对x0的传递函数为

根据该传递函数，在原有Ma、Ca、Ka参数不变的情况下，对比三参数模型与之前的两参数模型，分别取Kb=2Ka、Kb=4Ka、Kb=6Ka，如图8所示。

由图8可以看出，相比于两参数模型，三参数模型在高频段能获得更好的隔振特性，串联一个刚度后系统整体刚度下降，表现为共振峰频率减小，共振峰值增大，但是随着串联刚度逐渐增大，共振频率增大，共振峰值减小，即向两参数模型靠拢。

图8同时也证实了Kb取值的正确性，首先Ka与Kb串联之后的总刚度变小，要保证阻尼适当，Kb不能小于Ka；同时，Kb也不能过大，因为Kb越大，频响曲线越接近于两参数模型的频响曲线，对整体隔振效果不利。

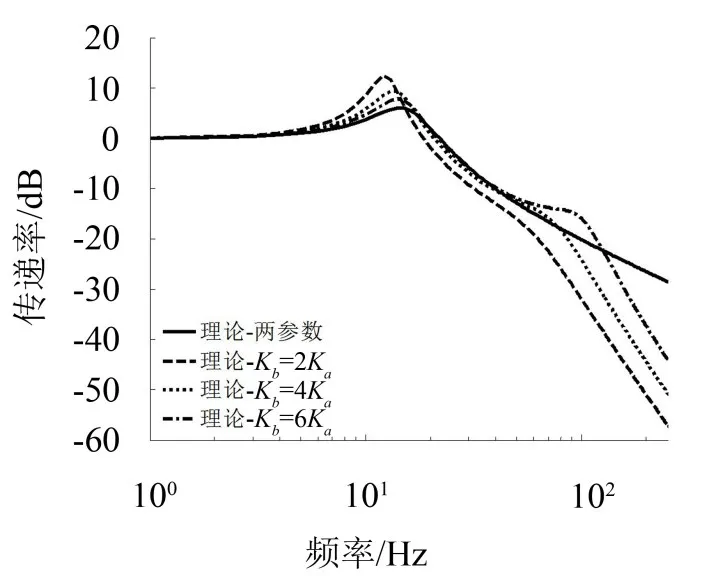
图8 三参数模型与两参数模型频响曲线对比

2.3 三参数隔振系统的隔振效果

在三参数模型验证的基础上，对三参数隔振系统的隔振效果进行测试。测试方案与两参数隔振系统一样，现场布置如图9所示。

图9 三参数隔振系统实验

通过振动台垂向激励，测得隔振系统的频响曲线如图10所示。由图10可以明显看出，曲线整体趋势与仿真结果吻合，验证了参数选择和计算模型的正确性。同时，以Kb=2Ka情况下传递曲线为例，曲线在60 Hz处传递率为-13 dB，在180 Hz处传递率为-38 dB，衰减率约为曲线中100 Hz左右的共振峰来源于附加质量Mb的影响，若Mb足够小，这1阶共振峰便不会出现。

在Kb=2Ka、Kb=4Ka、Kb=6Ka三种情况下，实测500 Hz内隔振前、后的振动响应，如图11所示。

对比500 Hz内隔振前、后的时域响应RMS值，结果如表1所示，从中可以看出，相比于隔振前，隔振后的RMS值均下降90%以上，隔振效果明显。

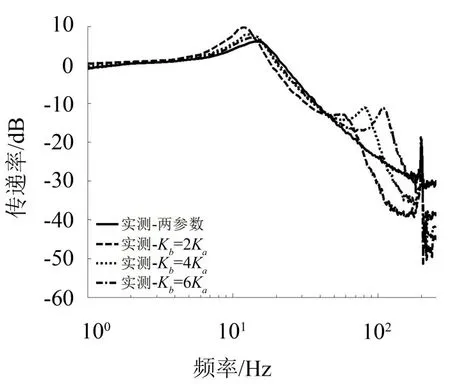
图10 三参数隔振系统实测频响曲线图

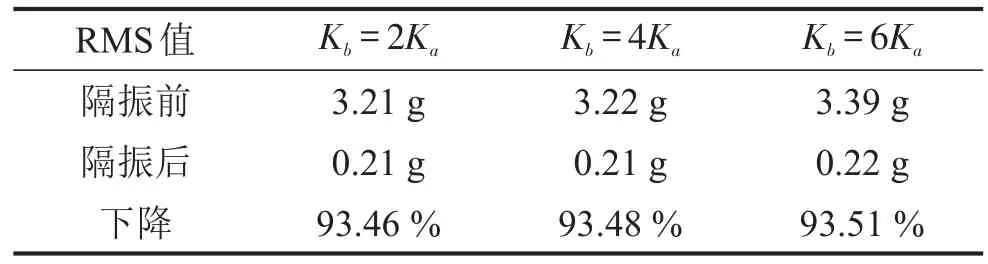
表1 隔振前、后时域RMS值对比

2.4 阻尼增大后三参数隔振系统的隔振效果

将两参数系统直接转变为三参数系统后，共振峰值增大，为抑制放大效应，通过减小阻尼孔的直径，将阻尼增大两倍。

图12为阻尼增大后测得的隔振系统频响曲线图。由图12可以看出，阻尼增大后，相比于图10，共振峰处的幅值明显得到抑制，其中Kb=4Ka、Kb=6Ka情况下的幅值分别只有4.91 dB与3.28 dB，共振峰放大倍数小。

将实测频响曲线与仿真曲线进行对比，如图13所示，可以看出，三参数模型仿真曲线与实测频响曲线吻合良好，验证了模型的正确性。因此，该模型可用于隔振器参数整定。

图14所示为阻尼增大后在Kb=2Ka、Kb=4Ka、Kb=6Ka三种情况下的实测隔振前、后时域响应曲线。

500 Hz内隔振前、后的时域响应RMS值，列于表2，可以看出，相比于隔振前，隔振后的RMS值均下降90%以上，与阻尼增大前相当。

图11 隔振前、后的时域响应比较

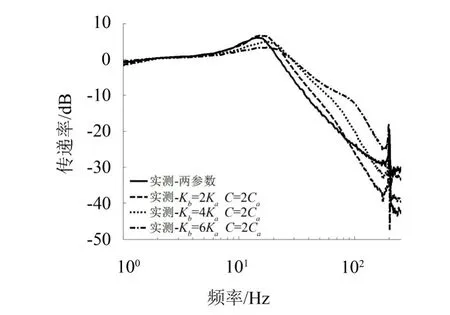
图12 阻尼增大后隔振系统频响曲线

图13 阻尼增大后实测频响曲线与仿真曲线对比

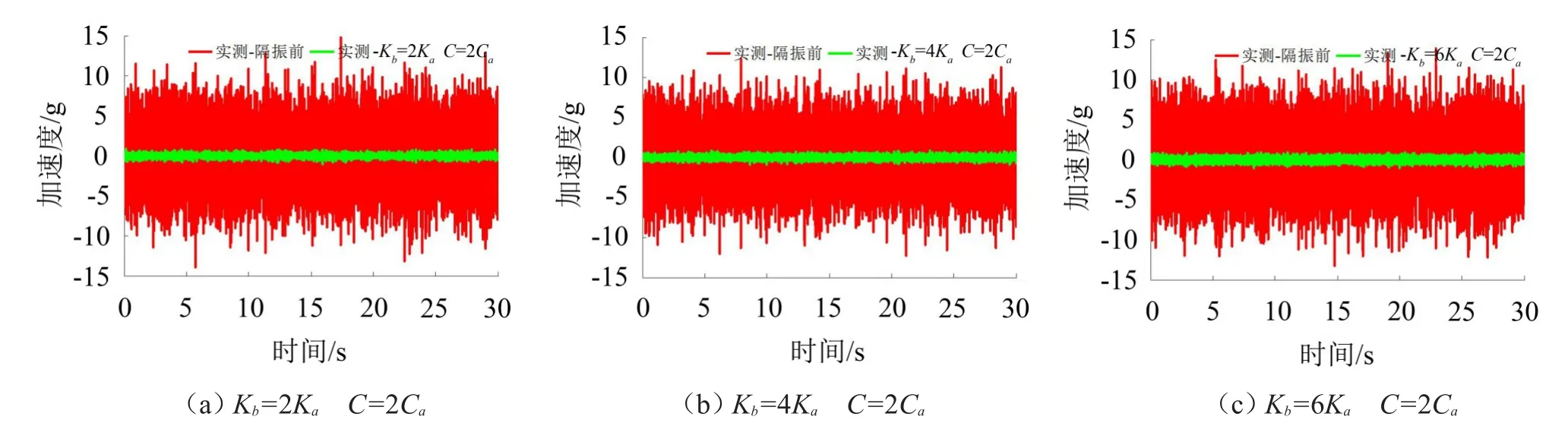
图14 阻尼增大后隔振前、后的时域响应比较

表2 隔振前、后时域RMS值对比

3 结语

采用焊接波纹管和黏滞流体构成的两参数隔振器，共振放大因子约为6 dB，高频段衰减率约为-30 dB/dec，通过串联弹簧和增大阻尼后，形成三参数隔振器，共振放大因子进一步降低，高频区衰减效果进一步改善。三参数隔振器的放大因子小于5 dB，高频段衰减率约为-52 dB/dec；在0～500 Hz内，隔振后的加速度RMS值下降90%以上。文中提出的隔振器可应用于对行程、动力放大因子和高频衰减率有较高要求的振动敏感型器件的隔振。

[1]DANELLE M T,JEREMY A W,KAREN S H,et al.MEMS reliability in a vibration environment[C].Proceedings of 38 th Annual 2000 IEEE International Reliability Physics Symposium,2000:139-145.

[2]LIU C,JING X,DALEY S,et al.Recent advances in micro-vibration isolation[J].Mechanical Systems and Signal Processing,2015,56:55-80.

[3]叶正强.黏滞流体阻尼器消能减振技术的理论、试验与应用研究[D].南京：东南大学，2003.

[4]孙靖雅.三参数流体阻尼隔振器及并联隔振系统的设计方法研究[D].上海：上海交通大学，2014.

[5]何玲.流体阻尼器特性及其对整星隔振性能影响的研究[D].哈尔滨：哈尔滨工业大学，2007.

[7]WANGC,CHEN Y,ZHANGZ.Simulationand experiment on the performance of a passive/active microvibration isolator[J].Journal of Vibration and Control,2016:DOI:10.1177/1077546316650130.

[8]DAVIS L P,WILSON J F,JEWELL R E,et al.Hubble space telescope reaction wheel assembly vibration isolation system[R].NASA Marshall Space Flight Center,Huntsville,Alabama,1986.

[9]DAVIS L P,CUNNINGHAM D C,DUNCAN D H.Three parameter viscous damper and isolator[P].U.S.Patent 5,332,070.1994.

[10]GAO X,CHEN Q,TENG H D.Modelling and dynamic properties of a novel solid and liquid mixture vibration isolator[J].Journal of Sound and Vibration,2012,331(16):3695-3709.

[11]GAO X,CHEN Q.Static and dynamic analysis of a high static and low dynamic stiffnessvibration isolator utilising the solid and liquid mixture[J].Engineering Structures,2015,99:205-213.

[12]WANG J,ZHAO S,WU D,et al.The interior working mechanism and temperature characteristics of a fluid based micro-vibration isolator[J].Journal of Sound and Vibration,2016,360:1-16.

[13]LEE D O,PARK G,HAN J H.Experimental study on onorbit and launch environment vibration isolation performance of a vibration isolator using bellows and viscous fluid[J].Aerospace Science and Technology,2015,45:1-9.

[14]LEE D O,PARK G,HAN J H.Hybrid isolation of micro vibrations induced by reaction wheels[J].Journal ofSound and Vibration,2016,363:1-17.

[15]CHEN Y,LU Q,JING B,et al.Dynamics of a passive micro-vibration isolator based on a pretensioned plane cable net structure and fluid damper[C].Journal of Physics:Conference Series.IOP Publishing.2016,744(1):012226.

[16]何小伟.考虑流体可压缩性的黏滞流体阻尼器理论与性能研究[D].上海：上海交通大学，2014.

[17]JIAO S,TIAN J,ZHENG H,et al.Modeling of a hydraulic damper with shear thinning fluid for damping mechanism analysis[J].JournalofVibrationand Control,2016:DOI:10.1177/1077546316629264.

[18]傅志方，华宏星.模态分析理论与应用[M].上海：上海交通大学出版社，2000.

Experiment of an Isolator Fabricated with Diaphragm Bellows and Viscous Fluid

XIE Xi-ling1,2,CHEN Yan-hao1,2,DIAO Jian-chao1,2,ZHANG Zhi-yi1,2
(1.Institute of Vibration,Shock and Noise,Shanghai Jiaotong University,Shanghai 200240,China;2.State Key Laboratory of Mechanical Systems and Vibration,Shanghai Jiaotong University,Shanghai 200240,China)

For the purpose of protecting sensitive payloads from vibrations,a vibration isolator with large strokes,low dynamic amplification factor and high attenuation rate is proposed.Firstly,a two-parameter vibration isolator composed of diaphragm bellows and viscous fluid is fabricated and experimented.The isolator has approximately an attenuation rate of-30 dB/dec at high frequencies and its resonance amplification factor is about 6 dB.Then,on the basis of theoretical analyses,a three-parameter vibration isolator is presented by connecting the two-parameter isolator to a series spring.By increasing the fluid damping,the isolation performance is improved.As a result,attenuation of vibration transmission at high frequencies is enhanced and the amplification factor is reduced.Experimental results demonstrate that the amplification factor of the three-parameter isolator is less than 5 dB and the attenuation rate is about-52 dB/dec.Moreover,after isolation,the RMS values of acceleration responses are reduced by more than 90%in the frequency range of 0-500 Hz.

vibration and wave;vibration isolation;diaphragm bellows;viscous fluid damping;three-parameter model

TB535

：A

：10.3969/j.issn.1006-1355.2017.04.040

1006-1355(2017)04-0201-05+230

2017-03-02

973计划资助项目（2014CB046302）

谢溪凌（1994－），男，安徽省芜湖市人，博士生，主要研究方向为振动控制。

张志谊（1970－），男，教授，博士生导师。

E-mail:chychang@sjtu.edu.cn