基于MDS和神经网络的滚动轴承故障诊断方法

马朝永，黄 攀，胥永刚，付 胜

(北京工业大学 机电学院 先进制造技术北京市重点实验室，北京 100124)

基于MDS和神经网络的滚动轴承故障诊断方法

马朝永，黄 攀，胥永刚，付 胜

(北京工业大学 机电学院 先进制造技术北京市重点实验室，北京 100124)

针对滚动轴承的智能诊断问题，提出基于多维尺度分析（Multidimensional Scaling，简称MDS）和神经网络的滚动轴承故障诊断方法。该方法首先提取原始信号常用的时域统计指标，再将包含故障信息的统计指标进行MDS降维处理，减少后续模式识别难度，最后将降维后的统计指标作为神经网络的输入参数来判断滚动轴承的故障类型。对滚动轴承正常状态、滚动体故障、外圈故障和内圈故障四种模式下的振动信号进行分析，结果表明，运用MDS进行降维预处理的神经网络故障诊断方法比没有经过预处理的故障诊断方法有更高的故障识别效率，可以准确有效识别滚动轴承的故障类型。

振动与波；滚动轴承；多维尺度分析；神经网络；故障诊断

在滚动轴承故障诊断中，时域统计量信息能有效诊断轴承是否产生故障，并且简单有效，应用广泛，因此时域统计指标提取和分析一直都是研究者关注的问题[1]。程军圣等将时域统计量作为神经网络的输入参数来进行故障诊断，并取得良好效果[2]。常用的时域统计指标包括最大值、均方根值、方根幅值、绝对平均值、偏斜度、峭度、方差、波形指标、峰值指标、脉冲指标、裕度指标、峭度指标等，将有限参数作为神经网络的输入参数时，会丢失其他参数信息，致使信息不完整。因此选择合适的参数作为神经网络的输入参数是一个有待研究的问题。

程军圣等人在文献[2]中，利用LMD方法对原始振动信号进行分解，得到若干个PF分量，选择前m个高频段PF分量，利用各分量的偏斜度、峭度指标和能量作为神经网络的输入参数，不考虑其他时域指标，这是一个减少维数的办法。另外，对于原始轴承数据，可以提取出大量指标，选择合适的数据降维方法，在保持原始数据点之间关系的前提下，降低样本数据维数，以去除噪声的影响，降低模式识别过程中的计算复杂度。MDS是一种寻求保持数据点之间差异度的降维方法，要求在降低数据维度的同时保持数据点之间的联系[3–4]。由原始轴承信号数据提取的时域指标矩阵An×m（n是样本点数，m是样本维度）经过MDS降维处理后，在低维空间得到对应的矩阵Bn×k（k＜m）。矩阵Bn×k保持了各点之间的差异度，继承了原始矩阵数据点之间的联系。通过MDS降维处理能够有效地减少数据处理量，最大程度地保留原始数据的拓扑结构[5]。人工神经网络具有很强的自组织、自学习能力，具有非线性模式分类性能，在滚动轴承故障诊断中得到广泛应用[6-9]。而神经网络的识别效果与提取的特征参数有关，因此轴承特征参数的提取与选择是其故障诊断的关键问题之一[10–11]。

文中拟将MDS算法与BP神经网络算法相结合，对滚动轴承进行故障诊断。从原始轴承信号样本中提取均值等13个时域统计指标，组成指标矩阵An×m。计算样本数据的差异度矩阵，在保持样本差异度矩阵的前提下，求得低维矩阵Bn×k，进一步将低维矩阵Bn×k作为神经网络的输入参数，采用神经网络的输出对滚动轴承的工作状态进行识别。为了验证MDS方法的优越性，将有MDS降维预处理和无预处理两种情况进行比较，即将原始信号提取的指标直接输入神经网络进行训练，用来识别滚动轴承的工作状态。实验结果表明，基于MDS的神经网络方法有更高的识别率。

1 MDS方法

MDS方法的本质就是在低维空间寻求一个矩阵Bn×k，使得Bn×k能够保持高维矩阵An×m数据点之间的联系。对于m维空间n个点x1、x2、…、xn组成的样本，其MDS降维过程如下[12]。

（1）计算距离矩阵D（drs是矩阵D的元素，表示xr和xs之间的距离），D是对角线全为0的实对称矩阵，计算

由式（1）可得

（2）定义内积矩阵B（brs是矩阵B的元素），其中

由式（2）可以得到

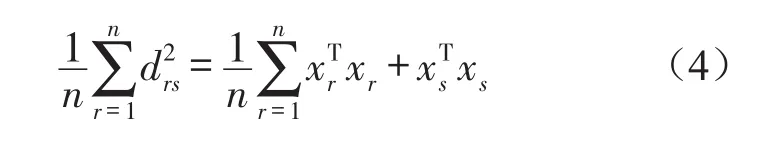
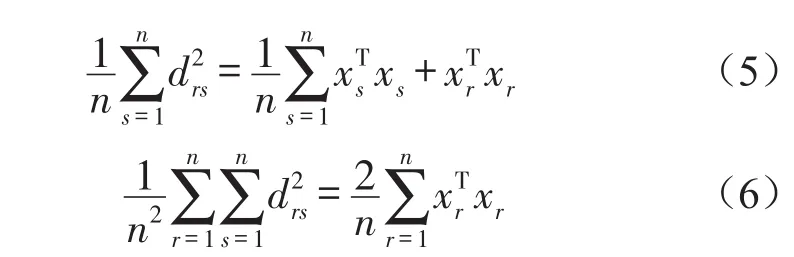
由式（3）至式（6）可得

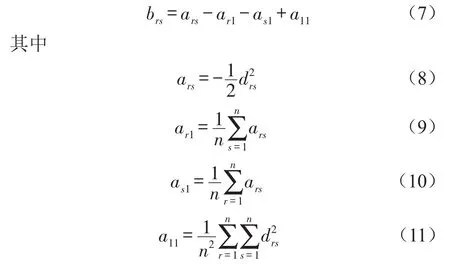
故可以由矩阵D得到B

（3）计算矩阵B的k个最大特征值以及其对应的特征向量；

2 基于MDS和神经网络的轴承故障诊断

在滚动轴承运行过程中，一般随着故障程度变得严重，均方根值、方根幅值、绝对平均值、峭度及峰值会不同程度的增大，其中峭度最为敏感。而峭度指标、裕度指标、脉冲指标对脉冲故障比较敏感。因此在做指标分析时，应当从多个指标角度来分析轴承的运行状态，而不是从单一的指标来分析。

考虑此因素，从原始轴承信号样本中提取以下时域统计指标：均值Xm、均方根值Xrms、方根幅值Xr、绝对平均值aXm、偏斜度α、峭度β、方差Dx、波形指标Sf、峰值指标Cf、脉冲指标If、裕度指标CLf、峭度指标Kv、峰值Xmax，将其组成指标矩阵An×m作为指标样本，经过MDS降维处理，保持原始样本点之间的联系，将降维后的矩阵作为神经网络输入参数，从而可以根据多指标角度判断滚动轴承的运行状态。基于MDS和神经网络的滚动轴承故障诊断方法流程如图1所示。

图1 基于MDS和神经网络的滚动轴承故障诊断流程图

（1）按一定的采样频率分别对滚动轴承四种状况（正常、滚动体故障、外圈故障、内圈故障）采样N次，得到n=4×N个样本；

（2）对原始信号进行指标提取，得到指标矩阵Sn×13，指标矩阵有n个数据点、13个指标维度；

（3）对Sn×13进行降维处理，将数据降到2维空间，得到低维矩阵Tn×2，低维矩阵Tn×2保持了原始样本点之间的联系；

（5）用训练好的数据对测试样本进行故障诊断。

3 实验结果

实验系统由轴承实验台、HG3528A数据采集仪、笔记本电脑组成。不同点蚀轴承依次安装在轴承实验台上，进行实验数据的采集。轴承的大径D=80 mm，小径d=35 mm，滚动体个数为z=8，接触角α=0。电机为恒转速，其转速r=1 496 r/min。实验时采样频率为15 360 Hz，采样点数为8 192，各种类型数据采样N=40次。采集到样本数据如图2所示，限于篇幅，图2只给出了4个样本点的时域波形及频谱。

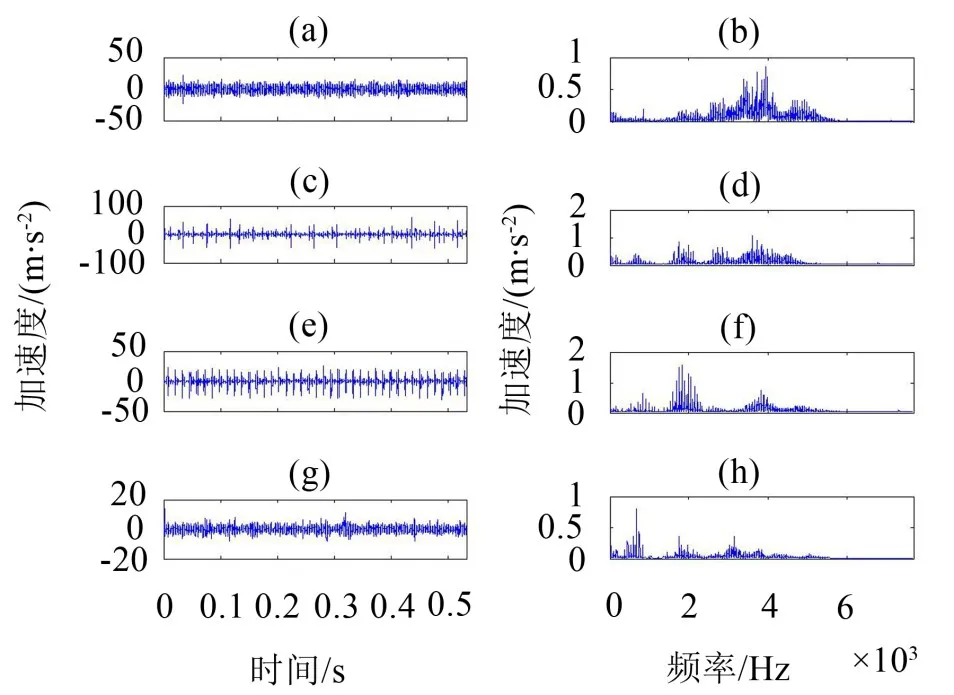
图2 样本数据的时域波形及频谱

对原始信号进行指标提取后，进行MDS降维处理，图3为降维后数据点集的分布。从图3可以看出，4种类型的数据点集基本能分离，保持了原始数据点之间的关系。采用BP网络进行分类，网络结构为2×12×4，分别将滚动体故障、内圈故障、外圈故障和正常的轴承4种模式的输出矩阵的状态编码为：滚动体故障[1,0,0,0]，内圈故障轴承[0,1,0,0]，外圈故障轴承[0,0,1,0]，正常轴承[0,0,0,1]。每种模式分别用30组数据进行训练，截止误差0.000 1，迭代次数5 000。用训练好的网络结构对40个测试样本进行分类识别，识别率达到97.5%，限于篇幅，表1只给出了4个基于MDS降维的神经网络故障识别的测试结果。将没有进行MDS降维的数据，随机取出两个指标，作为神经网络的输入参数进行训练，得到网络结构，识别率只有82.5%。表1给出了无预处理的4个测试样本的测试结果。

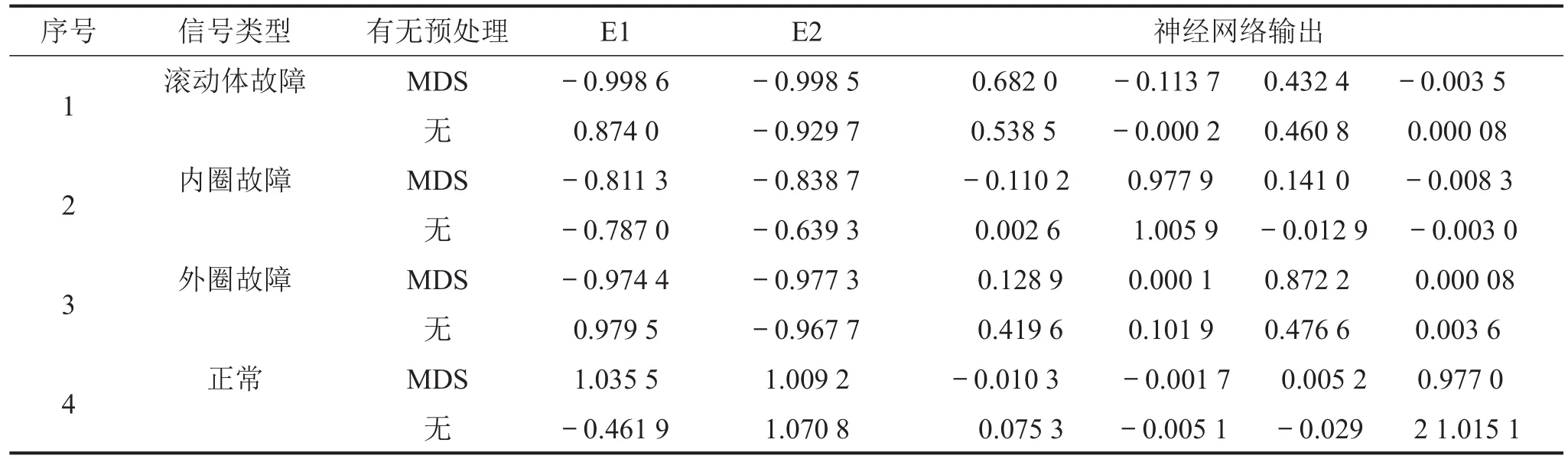
表1 有预处理和无预处理的滚动轴承故障识别结果

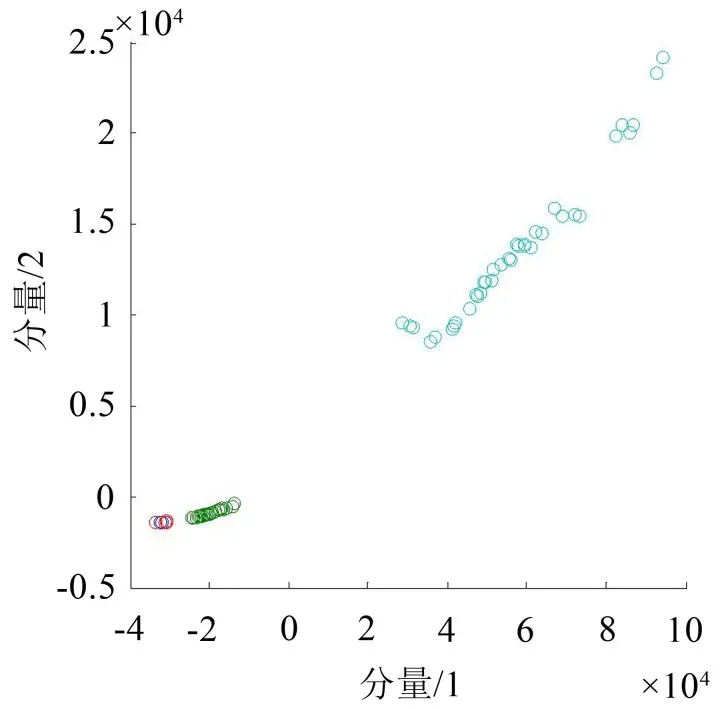
图3 降维后数据点集

由表1可知，这两种方法基本都能识别轴承故障类型，但基于MDS与神经网络的方法比没有预处理的方法有更高的识别能力。这是因为MDS降维后的低维数据保持了高维数据的信息，考虑了多个指标的影响，而随机取的两个指标只包含数据的部分信息，所以存在误分的情况。

3 结语

把MDS降维方法与BP神经网络相结合，用于滚动轴承的故障分类识别。

（1）MDS将高维空间数据投影到低维空间，在低维空间寻求一个低维矩阵可以保持原数据点之间的联系，因此，经过MDS降维处理的数据具有高维数据的特征信息。

（2）降维后的数据揭示了轴承故障的特征信息，可以作为基于神经网络的滚动轴承故障诊断的预处理方法。

（3）实验结果证明基于MDS和神经网络的滚动轴承诊断方法可以有效识别轴承的故障类型，比任意提取指标作为输入参数的神经网络具有更高的识别能力。

[1]孟宗，胡猛，谷伟明，等.基于LMD多尺度熵和概率神经网络的滚动轴承故障诊断方法[J].中国机械工程，2016，27(4)：433-437.

[2]程军圣，史美丽，杨宇.基于LMD与神经网络的滚动轴承故障诊断方法[J].振动与冲击，2010，29(8)：141-144.

[3]李先斌.应用多维尺度分析等方法进行H5N1禽流感病毒进化与传播机制研究[D].深圳：中国科学院深圳先进技术研究院，2014.

[4]谭璐.高维数据的降维理论及应用[D].长沙：国防科技大学，2005.

[5]赵一鸣.基于多维尺度分析的潜在主题可视化研究[D].武汉：华中师范大学，2013.

[6]刘贵立，张国英.基于小波包的遗传神经网络故障诊断系统研究[J].机械工程学报，2000，36(9)：110-112.

[7]CHEN XIANYUE,ZHOU JIANZHONG,XIAO HAN.Faultdiagnosis based on comprehensive geometric characteristic and probability neural network[J].Applied Mathematics and Computation,2010,230:542-554.

[8]WANG CHANGQING,ZHOU JIANZHONG,QING HUI.Fault diagnosis based on pulse coupled neural network and probability neural network[J].Expert Systems with Applications,2011,38:14307-14313.

[9]姜涛，袁胜发.基于改进小波神经网络的滚动轴承故障诊断[J].华中农业大学学报，2014，33(1)：131-136.

[10]杨宇，于德介，程军圣.基于EMD和神经网络的滚动轴承故障诊断方法[J].振动与冲击，2005，24(1)：86-88.

[11]焦李成.神经网络系统理论[M].西安：西安电子科技大学出版社，1990.

[12]王立强.基于多元统计图的高维数据降维方法及应用研究[D].秦皇岛：燕山大学，2006.

Rolling Bearing Fault Diagnosis Method Based on MDS and Neural Network

MA Chao-yong,HUANG Pan,XU Yong-gang,FU Sheng
（Key Laboratory ofAdvanced Manufacturing Technology,College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology,Beijing 100124,China）

A new fault diagnosis method for rolling bearings based on Multidimensional Scaling（MDS）and neural network is put forward.First of all,several time-domain statistics indexes of rolling bearings are extracted from original signals.Then,the indexes containing fault information are processed by MDS to reduce the data dimension.Finally,the low dimensional characteristic indexes are served as input parameters of neural network to identify fault patterns of the rolling bearings.The analysis results from rolling bearing signals with rolling element,inner-race and out-race faults show that the approach of neural network diagnosis based on MDS is superior to that without MDS and can identify roller’s fault patterns effectively.

vibration and wave;rolling bearing;multidimensional scaling;neural network;fault diagnosis

TH165+.3

：A

：10.3969/j.issn.1006-1355.2017.04.033

1006-1355(2017)04-0171-04

2017-01-20

国家自然科学基金资助项目(51375020)；北京市优秀人才培养资助项目（2011D005015000006）

马朝永（1970－），男，石家庄市人，博士，副教授，主要研究方向为汽车零部件检测、故障诊断。

E-mail:machaoyong@bjut.edu.cn