双界点OR值最大法logistic回归在中小学生登革热知识提高影响因素研究中的应用*

黄嘉玲 何贤英 黄 辉 张晋昕△

双界点OR值最大法logistic回归在中小学生登革热知识提高影响因素研究中的应用*

黄嘉玲1何贤英2黄 辉3张晋昕1△

目的 探讨双界点OR值最大法logistic回归在中小学生登革热知识提高幅度的影响因素研究中的应用。方法 基于多阶段分层整群随机抽样的广州市中小学生登革热相关知识传播效果的干预研究的调查数据，建立中小学生登革热知识提高幅度影响因素的双界点OR值最大法logistic回归模型，与采用连续型变量法、中位数法、单界点P值最小法的logistic回归模型比较模型拟合效果，探讨双界点OR值最大法logistic回归的优势。结果 纳入干预效果评估的共1311人，三年级299名，五年级331名，初二321名，高二360名。以高二数据为例，双界点OR值最大法logistic回归纳入的自变量为知识基线得分、干预方式、登革热病例数；其模型的拟合效果最好，且对于自变量分界点的划分更合理，能够更好地筛选出与结局有关联的影响因素。结论 双界点OR值最大法logistic回归适用于中小学生登革热知识提高幅度影响因素的研究。中小学生的登革热知识的干预效果受多个因素的影响，应开展有针对性的健康教育。

logistic回归 双界点OR值最大法 登革热相关知识 影响因素

登革热是一种由登革热病毒引起的急性传染病，主要通过埃及伊蚊和和白纹伊蚊叮咬人体传播。近年来，广东的登革热发病率位居全国最高［1］，其中广州在2014年累计报道登革热病例37341例［2］。目前，登革热尚无有效的疫苗预防。面对疫情威胁，重点还是要大力开展健康教育，动员广大群众积极参与到防蚊灭蚊中［3］。登革热相关知识在登革热的防控中扮演着非常重要的角色，加强登革热知识的健康教育有利于提高登革热的防控行为从而有效预防登革热［4-5］。中小学生是易受蚊虫叮咬的弱势群体，针对中小学生进行登革热知识的健康教育是登革热防控的重要组成部分。本文拟基于广州市中小学生登革热相关知识干预研究的调查数据，探讨双界点OR值最大法［6］logistic回归模型在中小学生登革热相关知识提高幅度的影响因素分析研究中的应用，同时跟其他常用的3种自变量处理方法［7-9］对比模型的拟合效果，为下一步干预工作的开展提供依据。

对象与方法

1．数据来源

数据来源于中山大学公共卫生学院参与的关于动漫游戏对广州市中小学生登革热相关知识传播效果影响的干预研究。采取多阶段分层整群随机抽样的方法，从广州市荔湾区、白云区抽取了12间中小学校。在上述中小学三年级和五年级、初二、高二各随机抽取2个班，以班为单位随机分到游戏组和阅读组。完成基线调查的合格问卷共1608份，最终纳入效果评估的问卷共1311份（完成基线调查、干预、干预后问卷调查），其中男生653名，女生656名（有2份问卷未填性别），三年级299名，五年级331名，初二321名，高二360名。选取干预后登革热相关知识提高幅度（以提高分数的中位数为界，≥4分设为1，＜4分设为0）作为因变量，相关的影响因素作为自变量，比较下述4种方法处理数据后拟合logistic回归模型的效果。

本数据包含可能影响登革热相关知识提高幅度的变量有：性别、年级、常住地（城乡）、干预方式、是否使用电脑上网、家长是否反对玩电子游戏、是否认为电子游戏有益、是否愿意通过游戏学习健康相关知识、平时是否玩电子游戏、近一周是否参与清理蚊子孳生地、登革热相关风险意识基线值、登革热相关行为把握度基线值、学习过程满意度评分、去年同校师生登革热病例数和知识基线得分。除了上述后面五个变量为连续型自变量外，其他均为分类变量。

2．连续型自变量和logitπ单调变化关系以及混杂因素的判断

logistic回归中要求连续型自变量与研究结局之间满足线性关系，否则可能得出影响因素和结局之间虚假的联系［10］。一般对连续型自变量取值进行合理的分类可以解决自变量和结局之间的非线性关系。本文采用半参数回归模型对连续型自变量和logitπ的函数关系进行判断，根据自由度是否大于2，判断自变量和logitπ之间是否满足线性关系［11］。

当连续型自变量和logitπ不满足线性关系时，在对其进行处理前，本文先判断是否存在混杂因素，如年级、性别等。若存在混杂因素，先按其分层，再进一步在每层内探讨连续型自变量与logitπ的单调变化关系。

3．连续型自变量参与拟合logistic回归模型前的4种预处理方法

在分层分析中，当连续型自变量和logitπ仍不满足线性关系时，分别采用目前常用的3种处理方法及双界点OR值最大法对原始数据进行预处理，进而结合其他在单因素logistic回归分析中P值小于0．2的变量去拟合多因素logistic回归模型，采用向前LR方法筛选自变量，检验水准为0．05。

（1）连续型变量法［7］，即连续型自变量直接参与回归分析。

（2）中位数法［8］，将连续型自变量的中位数作为分界点，转化为二分类变量纳入回归分析。

（3）单界点P值最小法（Min_P）［9］，该方法将连续型自变量的每一个取值都作为可能的潜在分界点，对所有潜在界点二分类分析并比较分析结果，选择使P值最小的自变量取值作为分界点，据此转化为二分类变量参与回归分析。

（4）双界点OR值最大法（Max_OR），首先绘制连续型自变量和logitπ的函数关系图（如图1），然后从logitπ值最大的位置出发，用平行于x轴的直线横切曲线，并向下平移。每次横切得到两个交点，将两个交点对应的自变量范围按照高、低风险将其重新赋值为二分类变量，再拟合logistic回归模型，得到OR值。最后，选择使OR值达到最大值时对应的自变量赋值方案作为最终的分类依据，转化为二分类变量再纳入回归分析。

4．模型效果的评价

模型效果的评价主要考虑两方面的内容，模型的拟合优度和变异的解释程度。其中拟合效果的评价采用-2 Log likelihood和AIC准则；变异程度的解释采用Cox＆Snell R Square、Nagelkerke R Square系数进行评价。

5．软件实现

采用Epidata 3．1软件进行双人双录入资料，使用R i386 3．3．1软件完成全部数据分析。

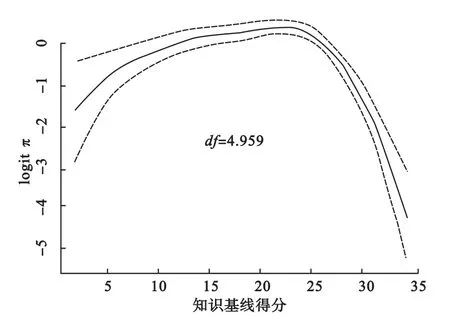
图1 自变量和logitπ的函数关系图（n＝1311）

实例分析结果

1．自变量与logitπ的函数关系图及混杂因素的判定（n＝1311）

对所有纳入效果评估的研究对象的数据（n＝1311）采用半参数回归模型判断连续型自变量和logitπ的函数关系，其中只有“知识基线得分”与logitπ不满足单调变化关系（见图1，df＝4．959），其余连续型自变量与对应的logitπ符合线性关系（略）。

方差分析的结果表明，4个年级的知识基线得分差异有统计学意义（F＝137．806，P＜0．001）。4个年级的知识得分的提高幅度有差异（χ2＝16．648，P＜0．001）。提示年级是影响“知识基线得分”和知识提高幅度之间关联强度的混杂因素。因此，先对年级分层，再探讨自变量“知识基线得分”和logitπ的函数关系。比较基线知识得分和知识得分提高幅度在男女之间的差异，结果均无统计学意义（P值均大于0．1）。

2．自变量与logitπ线性关系判定（按年级分层）

图2表示根据年级进行分层，分别对每个年级的数据采用半参数回归模型拟合得到自变量“知识基线得分”和logitπ的函数关系图。图2（a）中自由度等于2，说明在三年级里，连续型自变量“知识基线得分”和logitπ满足线性关系。图2（b）、图2（c）和图2（d）中均自由度大于2，说明分别在五年级、初二和高二年级里，连续型自变量“知识基线得分”和logitπ不满足线性关系。

三年级学生的知识基线得分与logitπ呈单调变化关系，直接采用连续型自变量法来拟合logistic回归模型。单因素logistic回归结果表明，对于三年级的学生，尚不能认为知识基线得分跟知识提高幅度有关（OR＝1．000，95．0%CI为0．966～1．036）。

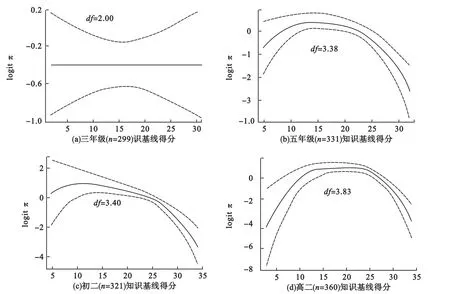
图2 自变量和logitπ的函数关系图（4个年级）

3．用4种方法处理自变量并拟合logistic回归模型的效果（高二）

表1为对高二的数据采用上述4种方法处理自变量“知识基线得分”后拟合多因素logistic回归模型的信息汇总表。表2为高二的数据采用4种处理方法拟合多因素logistic模型的效果比较。

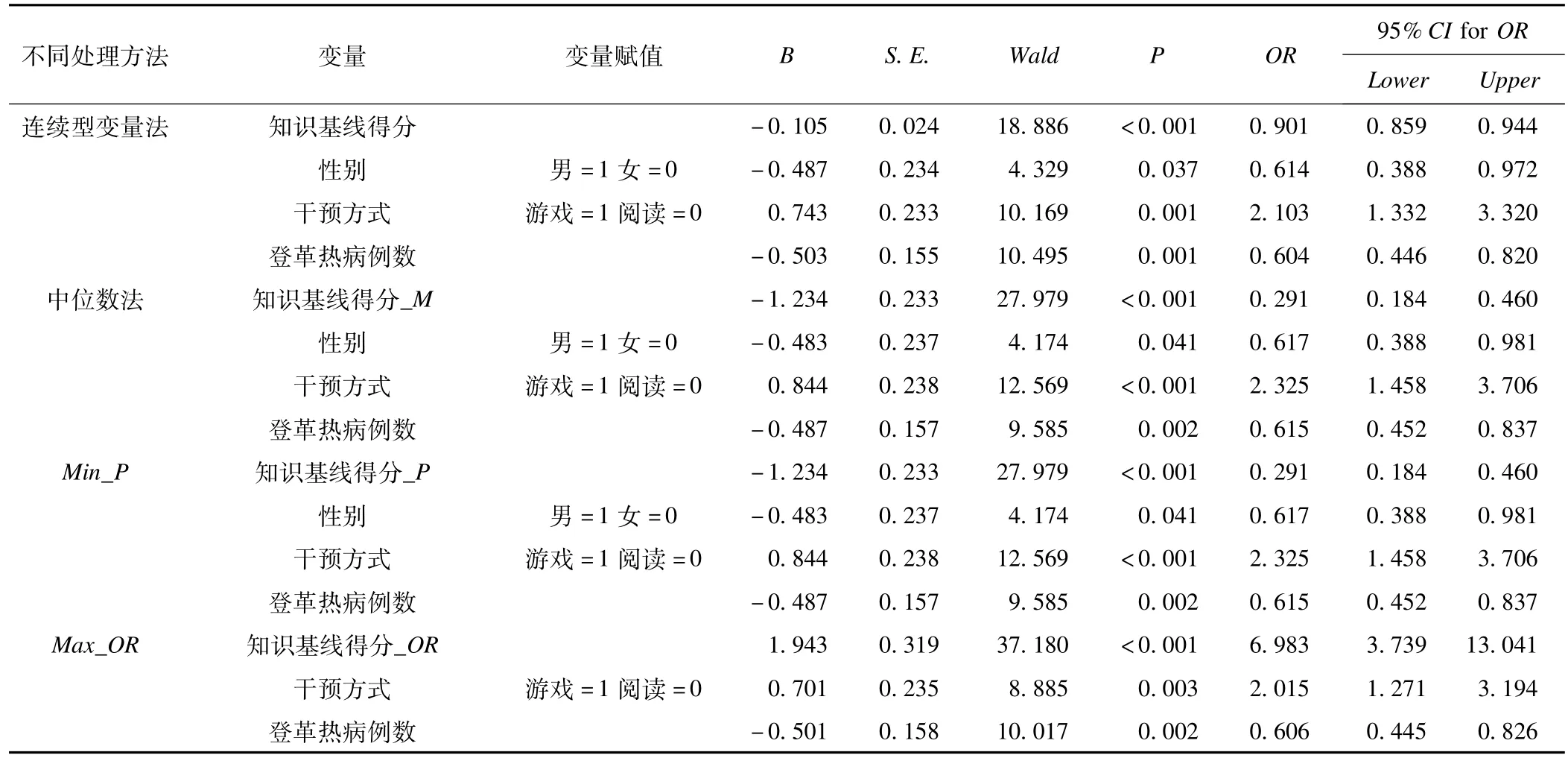
表1 高二学生数据拟合logistic回归模型信息汇总表

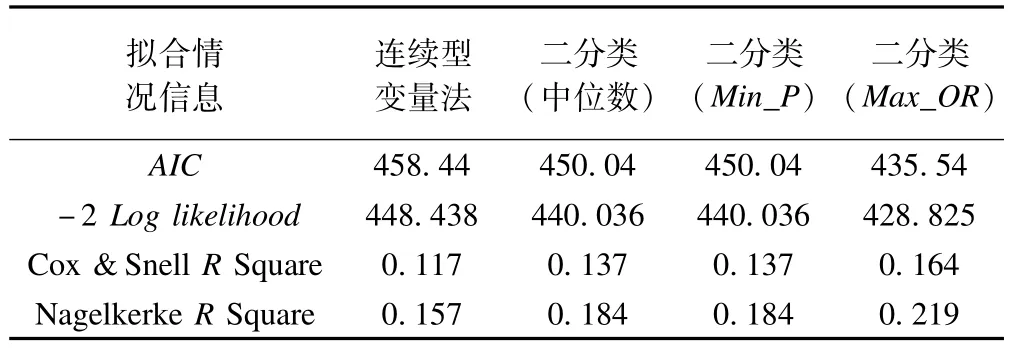
表2 不同处理方法模型拟合效果比较（高二学生数据）

表1结果表明，连续型变量法、中位数法和单界点P值最小法均纳入知识基线得分、性别、干预方式和登革热病例数这4个自变量。连续型变量法的结果提示，在校正了其他变量的影响后，登革热相关知识的基线得分越低的高二学生的知识提高幅度越高（OR＝0．901，95．0%CI为0．859～0．944）。中位数法和单界点P值最小法的结果提示，在控制了其他3个影响因素后，高二的学生中，知识基线得分25分及以上的个体的登革热知识提高幅度低于基线为25分以下的个体（OR＝0．291，95．0%CI为0．184～0．460）。双界点OR值最大法筛选出知识基线得分、干预方式和登革热病例数这3个变量，说明在控制了其他2个变量的作用后，知识基线得分位于中等水平的高二学生的登革热知识提高幅度较高（OR＝6．983，95．0%CI为3．739～13．041），并且提示在校正了其他影响因素的作用后，尚不能认为性别、通过电子游戏学习健康相关知识的态度与登革热相关知识的提高有关联。

由表2可见双界点OR值最大法模型拟合效果最好，表现在其AIC、-2 Log likelihood值最小，Cox＆Snell R Square、Nagelkerke R Square最大。由此可见，双界点OR值最大法能够根据数据特征，更合理地量化自变量“知识基线得分”和结局之间的联系，更好地筛选出与结局有关联的影响因素，且模型的拟合优度、变异的解释程度均比目前常用的分类法效果好。

分别对五年级、初二两个年级的数据采用上述4种方法处理自变量“知识基线得分”后拟合logistic回归模型并进行效果比较。结果显示，与中位数法和单界点P值最小法相比，双界点OR值最大法模型拟合效果最好，表现在其AIC、-2 Log likelihood值最小，Cox＆Snell R Square、NagelkerkeR Square最大；因篇幅所限，略去。

讨 论

logistic回归分析的前提条件要求连续型自变量和logitπ之间满足线性关系［12］，但在实际应用中该条件很容易被忽视［13］。当该条件不满足时，一般根据自变量和logitπ之间函数关系的具体形式选择适宜的方法对自变量取值进行分类处理。目前常用的分类方法有中位数法和单界点P值最小法。然而，中位数法未考虑同一组内个体应具有同质性，并且导致不同研究团队间结果横向比较的困难［14］；单界点P值最小法会导致低、高风险组比较时部分风险抵消。双界点OR值最大法将OR值最大化作为寻找分界点的判定原则，OR值不仅能反映自变量和结局有无关系并且能充分概括这种关系的强弱。本文以广州市中小学生登革热相关知识的干预研究的调查数据为基础，采用4种自变量处理方法处理自变量“知识基线得分”后拟合多因素logistic回归并进行效果比较。结果表明，双界点OR值最大法的AIC、-2 Log likelihood值最小，而且对于自变量界点的划分和影响因素的筛选更合理。

以高二数据为例，连续型变量法、中位数法和单界点P值最小法的结果显示，在校正其他变量的影响后，知识基线得分较低的学生的学习效果好。这与一般常识相悖。中位数法和单界点P值最小法把基础较差和基础中等的学生划分为一组，错误地认为两者学习效果相近。双界点OR值最大法的结果提示，基础较差（基线得分低于11分）的高二学生的学习效果较差，这对下一步的干预，如加强对基础较差的学生的教育，有指导意义。本研究发现游戏组的登革热知识的提高幅度优于阅读组，这与其他健康教育领域的研究结论一致，如营养、糖尿病等领域均有文献报道游戏的教育效果较好［15-16］。Ivan L．Beale等的研究提示游戏的干预方式能有效提高青少年癌症相关的知识和自信心，而且效果优于对照组［17］。这提示有必要加强游戏形式的登革热健康教育，从而提高教育效果。跟另外3种方法相比，双界点OR值最大法的模型并没有纳入性别变量，提示在考虑到基础较差以及其他因素的作用后，尚不能认为男女的学习效果有差异，这显然更符合实际。

本研究采用的实例数据中观察到的混杂因素只有年级，而且为了对不同年级提出针对性的干预措施，本研究在每个年级层面探索影响研究结局的因素。一般认为，应选择符合数据特征和研究目的的方法来控制混杂因素［18］。因此，本文对年级进行分层，而不是直接将年级作为协变量纳入logistic回归，否则会得到三年级学生的知识基线得分与知识提高有关联的虚假联系。

综上所述，双界点OR值最大法logistic回归适用到中小学生登革热知识提高幅度影响因素的研究，得到的模型具有更好的解释性。中小学生的登革热知识的教育效果受多个因素的影响，应针对不同年级、知识基线不同的学生开展有针对性的、形式丰富的健康教育。

［1］Fan J，Lin H，Wang C，et al．Identifying the high-risk areas and asso-ciated meteorological factors of dengue transm ission in Guangdong Province，China from 2005 to 2011．Epidem iol Infect，2014，142（3）：634-643．

［2］Cheng Q，Jing Q，Spear RC，et al．Climate and the Tim ing of Imported Cases as Determ inants of the Dengue Outbreak in Guangzhou，2014：Evidence from a Mathematical Model．PLoS Negl Trop Dis，2016，10（2）：e4417．

［3］Ho T，Huang M，Wang S，et al．Know ledge，attitude，and practice of dengue disease among healthcare professionals in southern Taiwan．Journal of the Formosan Medical Association，2013，112（1）：18-23．

［4］Al-Dubai S A，Ganasegeran K，Mohanad R A，et al．Factors affecting dengue fever know ledge，attitudes and practices among selected urban，sem i-urban and rural communities in Malaysia．Southeast Asian J Trop Med Public Health，2013，44（1）：37-49．

［5］Castro M，Sanchez L，Perez D，et al．The relationship between econom ic status，know ledge on dengue，risk perceptions and practices．PLoSOne，2013，8（12）：e81875．

［6］何贤英，赵志，温兴煊，等．logistic回归中连续型自变量离散化为二分类变量时适宜分界点的确定．中国卫生统计，2015，32（2）：275-277．

［7］Schellingerhout JM，Heymans MW，et al．Categorizing continuous variables resulted in different predictors in a prognostic model for nonspecific neck pain．Journal of Clinical Epidem iology，2009，62（8）：868-874．

［8］Knüppel L，Hermsen O．Median split，k-group split，and optimality in continuous populations．AStA Advances in Statistical Analysis，2010，94（1）：53-74．

［9］W illiams B，Mandrekar J，Mandrekar S，et al．Finding Optimal Cutpoints for Continuous Covariateswith Binary and Time-to-EventOutcomes．In Technical Reports Series＃79 Rochester，MN：Department of Health Science Research，Mayo Clinic，2006．

［10］Wand H，Ram jee G．Analyzing Continuous Measures in HIV Prevention Research Using Sem iparametric Regression and Parametric Regression Models：How to Use Data to Get the（Right）Answer？．AIDS and Behavior，2012，16（6）：1448-1453．

［11］陈长生，徐勇勇，夏结来．半参数回归模型及模拟实例分析．中国卫生统计，2001，28（6）：18-20．

［12］Jewell N P．Statistics for Epidem iology．1 edition．Chapman and Hall／CRC，2003：179-198．

［13］冯国双，陈景武，周春莲．logistic回归应用中容易忽视的几个问题．中华流行病学杂志，2004，（6）：92-93．

［14］MacCallum RC，Zhang S，Preacher KJ，et al．On the practice of dichotom ization of quantitative variables．Psychological Methods，2002，7（1）：19-40．

［15］Banos RM，Cebolla A，Oliver E，et al．Efficacy and acceptability of an Internet platform to improve the learning of nutritional know ledge in children：the ETIOBE Mates．Health Educ Res，2013，28，（2）：234-248．

［16］DeShazo J，Harris L，PrattW．Effective intervention or child′s play？A review of video games for diabetes education．Diabetes Technol T-her，2010，12（10）：815-822．

［17］Beale IL，Kato PM，Marin-Bow ling VM，et al．Improvement in cancer-related know ledge follow ing use of a psychoeducational video game for adolescents and young adults w ith cancer．J Adolesc Health，2007，41（3）：263-270．

［18］Li L，Kleinman K，Gillman MW．A comparison of confounding adjustmentmethods w ith an application to early life determ inants of childhood obesity．JDev Orig Health Dis，2014，5（6）：435-447．

（责任编辑：刘 壮）

Influencing Factors on Learning Effect of Dengue Related Know ledge of Primary and Secondary School Students：Application of M aximum OR Values M ethod in Logistic Regression

Huang Jialing，He Xianying，Huang Hui，et al（Department of Medical Statistics and Epidemiology，School of Public Health，Sun Yat-sen University（510080），Guangzhou）

Objective To explore the application of two cut-off points and maximum OR values method in logistic model for analyzing impact factors on the improvement of dengue related know ledge of primary and secondary school students．M ethods Maximum OR valuesmethod in logistic modelwas applied to themulti-stage stratified cluster random sampling data of the primary and secondary school students in Guangzhou to analyze impact factors on the learning effect of dengue related know ledge．In addition，themodel fitting effect of Maximum OR valuesmethod in logisticmodelwas compared w ith continuous variablesmethod，median splitmethod and one cut-off pointm inimum P valuesmethod．Results We enrolled a valid sample of 1311 students in evaluation of learning effect，containing primary 3，primary 5，junior 2 and senior 2 grades students．Maximum OR valuesmethod in logisticmodel retained variables of baseline know ledge scores，interventionmethod and dengue cases in data of senior 2，which presented the bestmodel fitting effect and performed better in screening out the impact factors related to outcome．Conclusion Two cut-off points and maximum OR valuesmethod in logistic model could be used to analyze impact factors on learning effect of dengue related know ledge of primary and secondary school students．There were multiple factors which influenced the learning effect of dengue related know ledge of primary and secondary school students，which are supposed to be developed aim measures of health education．

Logistic regression；Two cut-off points and maximum OR valuesmethod；Dengue related know ledge；Impact factors

广东省科技计划项目（2014A020212713）；广州市医药卫生科技项目（20141A010067）

1．中山大学公共卫生学院医学统计与流行病学系（510080）

2．郑州大学第一附属医院

3．广州市健康教育所

△通信作者：张晋昕，E-mail：zhjinx＠mail．sysu．edu．cn