含有Ⅱ型区间删失数据的回归模型参数估计*

山西医科大学卫生统计教研室（030001） 梁 洁 崔 燕 刘晓萌 顾彩姣 高 倩 王 彤

含有Ⅱ型区间删失数据的回归模型参数估计*

山西医科大学卫生统计教研室（030001） 梁 洁 崔 燕 刘晓萌 顾彩姣 高 倩 王 彤△

目的 比较四种方法估计含有Ⅱ型区间删失数据的回归模型参数最大似然估计值，探讨在不同样本量情况下四种方法估计结果的准确性和稳定性。方法 对含有Ⅱ型区间删失的生存数据分别拟合Weibull参数回归模型和Cox-PH半参数回归模型，并结合EM ICM算法得到模型参数的最大似然估计值；应用组均值插补法将区间删失数据填补为右删失数据，进一步用传统的Cox回归以及建立伪观察值的方法估计生存函数，模拟样本量分别为50、200、500例。结果 Weibull回归模型的参数最大似然估计值分别为β＾1＝0．496，β＾2＝-0．366；β＾1＝0．680，β＾2＝-0．586；β＾1＝0．620，β＾2＝-0．504。Cox-PH半参数回归模型的参数最大似然估计值为β＾1＝0．652，β＾2＝-0．469；β＾1＝0．683，β＾2＝-0．538；β＾1＝0．629，β＾

2＝-0．511。填补为右删失数据后传统Cox回归方法得到的参数最大似然估计值分别为β＾1＝0．203，β＾2＝-0．227；β＾1＝0．641，β＾2＝-0．514；β＾1＝0．545，β＾2＝-0．446。用Pseudo-observations得到的参数最大似然估计值分别为β＾1＝0．217，β＾

2＝-0．275；β＾1＝0．796，β＾2＝-0．601；β＾1＝0．561，β＾2＝-0．468。结论 在不同样本量情况下，拟合Weibull参数回归模型，Cox-PH半参数回归模型结合EM ICM算法估计的参数最大似然估计更准确更稳定。

Ⅱ型区间删失数据 最大似然估计 EM ICM算法 伪观察值

在生存分析中，通常需要对事件发生时间进行观测，进而分析评价。有些情况下，我们能够得到准确的生存时间，但是在多数情况下，由于观测目标的不稳定存在，或观测结束时事件仍在发生，只能得到不完全的观测数据。在进一步统计分析时，这些不完全的数据给分析者带来了许多困扰，若直接删掉会丢失信息。如何尽可能的利用不完全数据信息得到较为准确的分析结果，是生存分析的重要问题。区间删失数据是不完全数据中的一大类，在一些临床试验中会广泛地出现区间删失数据，即事件发生在某一给定的时间区间内，而观察者不知道确切的时间点。

根据不同的删失机制，区间删失可分为Ⅰ型区间删失、Ⅱ型区间删失、追踪计数删失、双变量区间删失以及双边区间删失［1］。其中Ⅰ型区间删失数据，也叫现况数据，指对研究对象只进行一次观察所得到的事件发生与否的信息，常发生在横断面研究和非致死性肿瘤致瘤性试验中，得到左删失或右删失数据［1］。而当所得观测数据中包括至少一个区间（L，R］，L，R∈（0，∞），L＜R时，我们称其为Ⅱ型区间删失数据，其观测时间点为相互独立的确定时间，即（L，R］中，L，R均为确定的观测时间点［1］。其主要发生在需要定期随访观察的研究中，比如AIDS的临床医学研究、肿瘤发病率的纵向研究，以及临床试验研究。这种删失机制是由于在实际随访中，部分患者未按照预先确定的观测时间进行观察，而是选择在较方便的时间进行观察；而有些患者可能会错过一个或多个观察后再继续进行观察［2］。因此不同患者的随访观察时间是不同的，研究者只能得到患者在出现某个结局之前最后一次临床观察的时间和出现此结局之后第一次临床观察的时间，即Ⅱ型区间删失数据［3］。其既不同于可以精确测得的数据，又不同于缺失数据，研究者应根据其提供的不完整的数据信息，估计出相对稳定的回归模型参数，从而解决临床实际问题。

本文应用Weibull参数回归模型，Cox-PH半参数回归模型以及经组均值插补法填补后结合传统Cox回归模型和建立伪观察值的方法，估计含有Ⅱ型区间删失数据的回归模型参数最大似然估计值。前两种方法结合（expectation maxim ization iterative convex m inorant，EM ICM）算法得到模型参数的最大似然估计值；组均值插补法［4］是将区间删失数据填补为右删失数据，进而通过拟合传统Cox回归模型以及建立伪观察值的方法得到参数的最大似然估计值。

原理与方法

假设区间删失信息与生存事件的发生相互独立，观测数据满足独立同分布，样本｛（Li，Ri］，Zi，i＝1，…，n｝，（Li，Ri］为区间删失Ti的观察窗，Zi是第i个观察单位的二维协变量矩阵，Ti独立于（Li，Ri］。Li＝Ri则代表Ti是精确的时间，Li＝0表示左删失，Ri＝∞表示右删失。S（t｜Zi）＝P（Ti＞t｜Zi）为给定Zi时，在固定点t＞0的Ti的条件生存函数。

1．Weibull回归模型

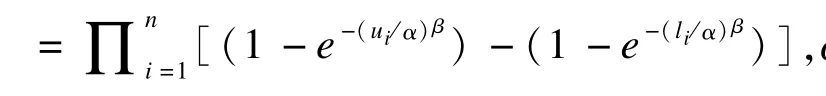
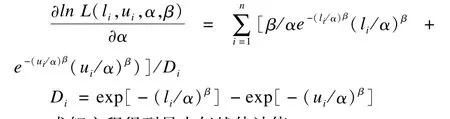
求解方程得到最大似然估计值。

2．Cox-PH模型

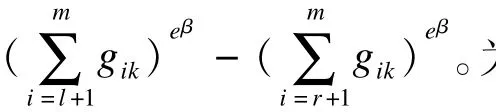
3．EM ICM算法

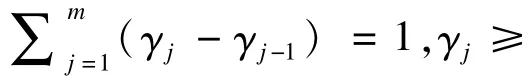
为了弥补EM算法的缺陷，ICM算法将最大似然估计的问题转化成为了线性规划的问题［8］。认为CX为Km-1的子空间，CX＝｛x＝（x1，…，xm-1）；0≤x1≤xm-1≤1｝。假设C是Km-1的凹锥，φ（X）是从Km-1到K连续可微凹映像的，令x＾＝argmaxx∈Cφ（X）。当X＾时已知的，φ（X）的最大值为下式的最大化：φ*（x｜y，W）＝，对应固定的y∈κm-1和正定对角矩阵：W＝diag（w1，…，wm-1）。ICM算法不需要线性寻求，EM迭代算法保证了ICM算法中似然函数的提升，两种方法反复映射，保证快速有效得到全局收敛。

4．伪观察值填补方法基本思想

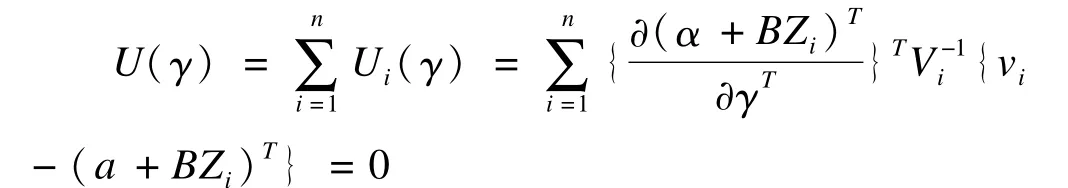
Vi为占νi相关性的工作协方差矩阵。标准的γ＾的“sandw ich”方差-协方差矩阵：

求解方程，得到生存函数S（t）的一致性估计。

5．模拟研究

考虑二维协变量Xi＝（Xi1，Xi2），协变量x1来自均匀分布runif（-1，1），协变量x2来自二项分布rbinom（1，0．5），设定协变量系数的真实值为β1＝0．5，β2＝-0．5。模拟样本量为50，200，500删失比例小于50%的数据集。根据不同删失比例对Cox模型估计结果的影响，删失率小于等于30%时，得到的模型偏倚性较小［12］，故设置小样本量（n＝50）删失率为小于30%；大样本量（n＝200，500）删失率为30%～40%。对在不同样本量情况下的含有Ⅱ型区间删失的生存数据分别拟合Weibull参数回归模型和Cox-PH半参数回归模型，结合EM ICM算法得到模型参数的最大似然估计值，模型估计应用R软件中的icenReg软件包；将区间删失数据填补为右删失数据，进一步用传统Cox回归以及建立伪观察值的方法估计生存模型，模型估计分别应用R软件中的survival，pseudo和geepack软件包。基于上述四种估计方法，比较协变量Xi＝（Xi1，Xi2）的估计效果。

模拟结果

在不同样本量情况下，模拟数据集的删失比例分别为22．0%，36．0%，34．4%。四种回归模型参数最大似然估计值如下：Weibull参数回归模型参数的最大似然估计值分别为半参数回归模型参数得到的最大似然估计值为；填补为右删失数据后通过Cox回归方法得到参数的最大似然估计值分别为填补为右删失数据后用Pseudo-observations得到参数的最大似然估计值分别为在样本量为50，删失比例为22．0%时，前两种方法估计的参数比较准确，但第二种方法得到的标准差估计量相对更小，即估计的有效性更高；在样本量为200，删失比例为36．0%时，前三种方法估计值的无偏性和有效性较高，第四种方法估计的准确性较差；在样本量为500，删失比例为34．4%时，四种方法的估计结果差异很小。经模拟发现在不同样本量情况下，前两种方法的估计结果比较稳定，准确性较高；同时当删失比例在30%～40%，样本量大的情况下，估计的结果更理想。因此对于含有Ⅱ型区间删失生存数据的回归模型参数估计，在不同样本量和删失比例条件下，Weibull参数回归模型，Cox-PH半参数回归模型结合EM ICM算法拟合参数最大似然估计的结果更准确和稳定。

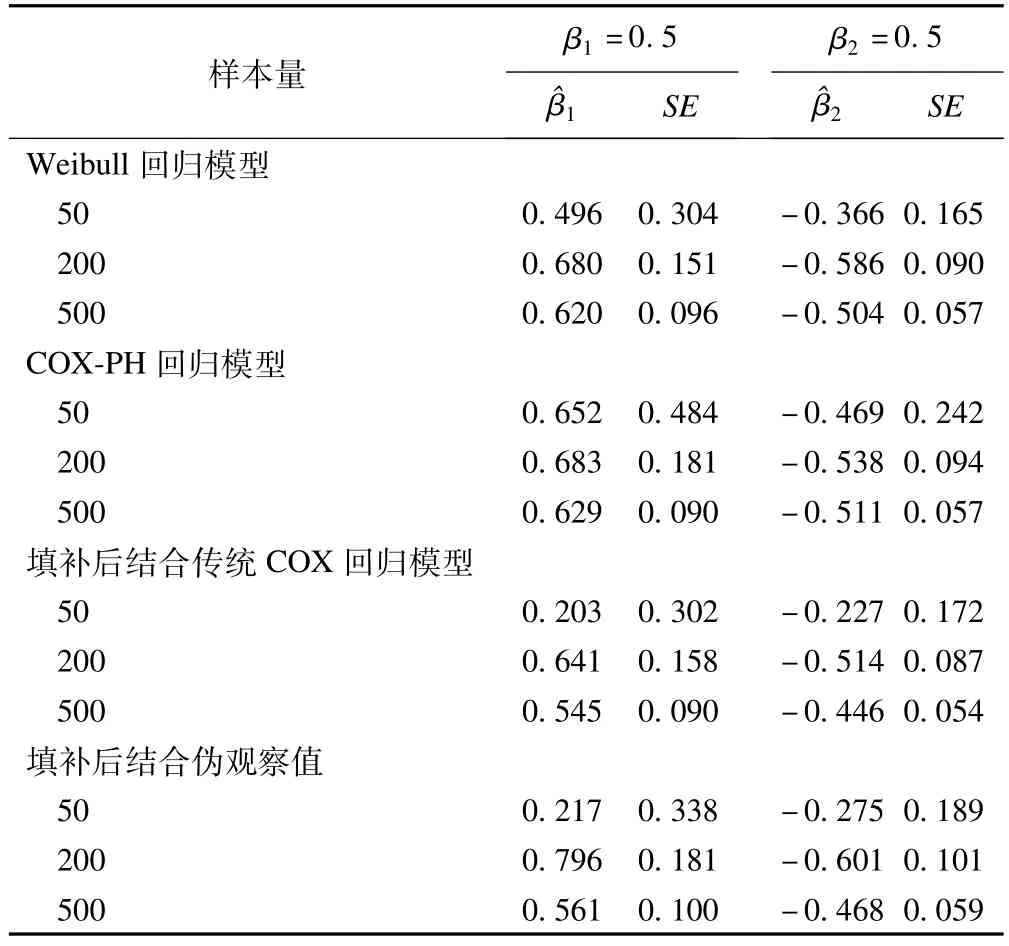
表1 含有Ⅱ型区间删失生存数据在不同样本量情况下不同回归模型参数估计结果

讨 论

区间删失数据是不完全数据中的一大类，在许多临床试验数据中都会存在，其中Ⅱ型区间删失数据既不同于可以精确测得的数据，又不同于缺失数据，如何根据其提供的不完整数据信息，估计出相对稳定的回归模型参数，从而解决临床实际问题是生存分析中值得被广泛关注的课题。目前，对于处理Ⅱ型区间删失数据的方法，国内学者多采用线性回归或样条函数构建模型，并结合EM算法或自相合算法估计模型参数，两种方法在处理此类数据时计算较为复杂，并且需要很多现实中难以满足的假设。由于Cox回归参数估计并不依赖于特定的分布，故其被广泛用于处理右删失数据的实际应用中，但对于区间删失数据，在求解最大似然估计值的过程中可能得不到闭集解，因此用EM ICM算法对含有此类数据的Cox回归进行参数估计，可得到较为理想的估计结果。

本文用四种方法对含有Ⅱ型区间删失数据的生存数据进行模型拟合，分别为Weibull参数回归模型、Cox-PH半参数回归模型以及将Ⅱ型区间删失数据填补为右删失数据后分别用Cox回归以及建立伪观察值的方法。通过模拟分析，我们发现在不同样本量情况下，前两种方法的模型拟合结果更准确；当删失比例在30%～40%，样本量大的情况下，估计的结果更理想。因此对于含有Ⅱ型区间删失生存数据的回归模型参数估计，在不同样本量条件下，Weibull参数回归模型，Cox-PH半参数回归模型结合EM ICM算法估计参数最大似然估计值的结果更加准确和稳定。由于右删失与Ⅱ型区间删失的删失机制不同，在将Ⅱ型区间删失数据转换为右删失数据过程中，可能导致一些信息的丢失，故后两种方法得到的估计结果不稳定。本文模拟只探讨了删失比例小于50%的情况，没有设定各样本量高删失比例与低删失比例的具体情况，但实际中，不同样本量的生存数据所包含的Ⅱ型区间删失数据删失比例各异，高删失比例将如何影响不同模型的拟合效果，应采用何种方法处理是我们下一步要解决的问题。此外，我们只考虑了包含两个协变量的情况，在实际情况中，协变量的个数可以是多个，那么较多协变量存在的情况下，形成了含有Ⅱ型区间删失数据的高维数据能否用这两种方法得到较好的模型估计，这是我们需要进一步考虑和验证的。目前，关于Ⅱ型区间删失数据的生存分析方法有很多，但都在探索阶段，即并没有某种方法被确定为处理此类数据的最优方案。因此在临床实践中，应针对不同的数据情况使用不同的模型拟合方法，并结合适当的协变量选择方法估计出更准确的模型。

［1］Sun J．The statistical analysis of interval-censored failure time data．American：Springer，2006．

［2］梁洁，王彤，崔燕．Ⅱ型区间删失数据的生存分析．中国卫生统计，2016，33（2）：357-362．

［3］张琴，丁邦俊．区间删失数据回归模型的参数估计．华东师范大学，2013：1-26．

［4］Xiao X．Study of an imputation algorithm for the analysis of intervalcensored data．Journal of Statistical Computation and Simulation，2012，84（3）：477-490．

［5］Pradhan B．Analysis of interval-censored data with weibull lifetime distribution．Sankhya：The Indian Journal of Statistics，2014，76-B（1）：120-139．

［6］Goetghebeur E．Semi-parametric regression analysis of interval-censored data．Biometrics，2000，5（6）：1139-1144．

［7］Cai T，Betensky RA．Hazard regression for interval-censored data with penalized spline．Biometrics，2003，59：570-579．

［8］Ding BJ．Regressionmodelw ith an interval-censored data covariant．Chinese Journal of Applied Probability and Statistics，2012．28（2）．

［9］Ao Y，YizhengW，Kepher M，etal．Approximate nonparametricmaximum likelihood estimation for interval censoring model case II．International Journal of Statistics and Probability，2014，3（3）：44-64．

［10］Graw F，Gerds TA，Schumacher M．On pseudo values for regression analysis in competing risks models．Lifetime Data Analysis，2009，15：241-255．

［11］Andersen PK，Perme MP．Pseudo-observations in survival analysis．Statistical Methods in Medical Research，2010，19（1）：71-99．

［12］陈雯，陈昂，夏英华，等．样本量及删失率对生存分析模型有效性和偏倚性的影响．中国卫生统计，2013，30（1）：5-8．

（责任编辑：郭海强）

Estimation of Regression M odel w ith the CaseⅡInterval-censored Failure Time Data

Liang Jie，Cui Yan，Liu Xiaomeng，et al（Department of Health Statistics，School of Public Health，Shanxi Medical University（030001），Taiyuan）

Objective Our study compares fourmethods to estimate themaximum likelihood estimators of regression model，which contains the typeⅡinterval censored failure data，and discusses the accuracy and stability of the results under the conditions of different sample size．M ethods The sample size was 50，200 and 500．We use the weibull regression model and Cox-PH model to fit the typeⅡinterval censored failure data．EM ICM arithmetic is used to estimate themaximum likelihood estimations of covariates．The imputations of right censored is estimated by traditional Coxmodeland pseudo-observations．Results

In the firstmethod，the estimators of parametrics based on weibullmodel were．While the estimators of parametrics based on Cox-PH model wer

CaseⅡinterval censored failure time data；Maximum likelihood estimation；EM ICM arithmetic；Pseudo observation

国家自然科学基金（81473073）

△通信作者：王彤，Email：tongwang＠sxmu．edu．cn