钼粉粒度影响因素的多元回归分析研究

程 进，肖江涛

(金堆城钼业股份有限公司金属分公司，陕西 西安 710077)

钼粉粒度影响因素的多元回归分析研究

程 进，肖江涛

(金堆城钼业股份有限公司金属分公司，陕西 西安 710077)

本文试图应用概率统计方法和软件工具对影响钼粉粒度的因素进行相关分析和多元回归分析研究，找出各主要因素与钼粉粒度是否存在相关关系以及其对钼粉粒度影响的显著性水平，获得可应用的多元线性回归方程，为钼粉制备提供更宏观有效的调控方法。

粒度;温度;装舟量;节拍;K;多元回归分析;残差

0 引 言

钼及其合金在冶金工业、电子工业、航空及化工等领域应用广泛[1]。随着科学技术的发展，产品不断更新换代，对钼及其深加工产品性能也提出了更高的要求，也促使人们对其展开了更深入的研究和探索。中国是一个钼资源大国，但是目前初级加工产品过剩，而深加工产品不足，种类不全，同时质量性能不稳定，严重制约了我国钼及其高端产品的应用，且仍有部分钼制品仍需进口。所以，大力发展高性能、高附加值的钼产品，取代进口产品，是中国钼业发展的战略任务[2]。

钼粉性质对后续深加工产品性能差异有着决定性的作用[3]。在进行钼粉制备或钼产品的深加工时，钼粉粒度是我们考虑最多、最广泛也最重要的一个物理指标。众所周知，影响钼粉粒度的主要因素有温度、装舟量(或者料层厚度)、节拍(即时间)、MoO3粒度以及K含量等[4]。工艺参数的选择很大程度上决定了钼粉的质量，在氢还原氧化钼的过程中，钼粉粒度的各主要影响因素(参数)之间的定量关系研究，基本未见文献报道。因此，利用大量的生产实验统计数据，结合相关分析和多元回归分析方法，找出各影响因素之间的定量关系，形成可利用的多元回归方程，为钼粉粒度稳定性的因素分析提供一种更全面、宏观的研究方式。

1 多元线性回归分析

回归分析的基本思想是：自变量与因变量之间虽没有严格的、确定性的函数关系，但可以设法找出最能代表它们之间关系的数学表达式[5]。研究在线性相关条件下，两个或两个以上自变量对一个因变量的数量变化关系，称为多元线性回归分析，表现这一数量关系的数学公式，称为多元线性回归模型。其主要解决以下几方面问题：(1)确定几个特定的变量之间是否存在相关关系，如果存在，找出它们之间合适的数学表达式；(2)根据一个或几个变量的值，预测或控制另一个变量的取值，并且可以知道这种预测或控制能达到什么样的精确度；(3)进行因素分析。如在对于共同影响一个变量的许多变量因素之间，找出哪些是重要因素，哪些是次要因素，这些因素之间又有什么关系等[6]。

2 生产试验数据选取

采用水洗高纯MoO3为原料进行两段氢气还原方式生产钼粉。一段反应设备为回转管还原炉，二段反应设备为十八管还原炉，所出钼粉过200目筛后进行费氏粒度测定并收集过程数据。

影响钼粉粒度的因素较多，为便于研究，我们稳定一段还原工艺不变，同时氢气流量等也均保持不变，只研究高纯MoO3及二段工艺的变化对钼粉粒度的影响。经过分析筛选后，最终确定主要因素为MoO3粒度、K含量、二段还原Ⅰ、Ⅱ、Ⅲ、Ⅳ温区温度以及装舟量、出舟数等共计8个影响因子。

笔者在本研究中基于以上实际生产试验筛选取近100组样品数据，每组因子数据均一一对应。其取值范围如表1，包含对应的高纯MoO3粒度、K含量、Mo粉粒度、二段还原Ⅰ、Ⅱ、Ⅲ、Ⅳ温区温度以及装舟量等数据，其中Ⅰ区为辐射温区，不可控。利用计算机软件中多元回归分析方法进行分析研究，找出各影响变量与钼粉粒度之间的关系，形成多元回归方程，研究该方程的有效性并加以预测检验。

表1 主要因子数据取值范围

3 结果与讨论

3.1 相关分析

3.1.1 影响因素与钼粉粒度关系

图1中，纵轴均为钼粉费氏粒度，横轴为影响因素。图1表明，Ⅰ、Ⅱ、Ⅲ、Ⅳ温区温度、装舟量与钼粉粒度存在一定相关关系，且为正相关；而MoO3粒度、K含量及出舟数则看不出明显关系。同时，从图1中可以看出，因实际生产参数的选择，部分因子中某段数据量可能较少，数据不均，其可能影响结果判断。而本文只是提供一种研究方法，故此问题不在本文过多赘述。

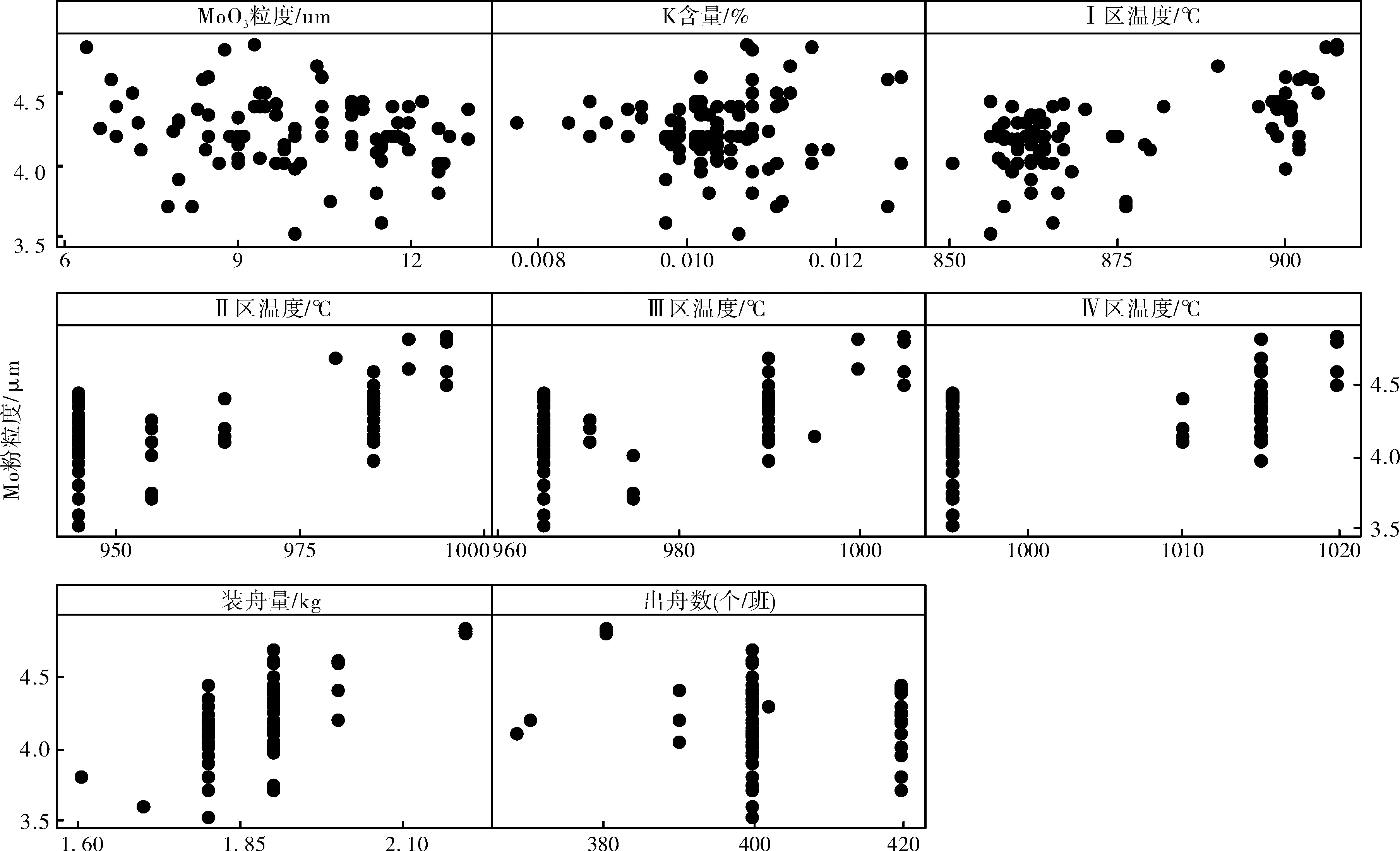
图1 钼粉粒度与影响因素的散点图

3.1.2 影响因素与钼粉粒度关系强弱

图1只能定性表明两者之间存在相关关系，并不能定量描述两者影响关系强弱。因此，为了定量分析它们之间的影响关系强弱，我们利用Minitab计算机软件进行分析，获得数据见图2。

图2 皮尔森相关分析

皮尔森相关系数描述的是两个变量之间线性相关强弱的程度，其绝对值越大表明相关性越强，取值介于0～1之间[7]。一般我们把相关系数∣r∣>0.5称为较强相关或强相关，表明两者之间存在较强及以上关系。从图2可以看出，装舟量与钼粉粒度相关关系最强；其次4个温区温度与钼粉粒度相关关系相差不大，而图1中看不出明显关系的3个因素中，在图2中则能看出MoO3粒度、装舟量则与钼粉粒度之间存在相关关系，但较前面5个影响因子要弱，为弱相关；最后，图2中K含量与钼粉粒度之间没有相关关系，这与图1一致。通过它们的P值也能看出它们之间是否存在相关关系,P≦0.05，则表明显著，否则不显著。同时，K含量的判断也与我们认知中K含量对钼粉粒度存在影响结论相悖，本文则不在此过多分析两者研究方法差异所导致的结论差异。

3.2 多元回归分析

3.2.1 建立多元回归模型

通过图1、图2分析后，确认本文中8个因子中除K含量与钼粉粒度不存在相关关系外，其他7个因子均存在相关关系，则利用Minitab软件进行回归分析，其分析结果见图3、图4。

3.2.2 回归模型分析

(1)首先，图3回归模型方差分析中，回归模型P值小于0.05，表明回归模型有效；同时回归模型中MoO3粒度、Ⅳ温区温度及装舟量因子的P值均小于0.05，表明其对模型影响显著，其他因子则不显著。其次，对应失拟项P值大于0.05，表明模型没有失拟现象；最后，R-sq及R-sq(预测)均不大，未达80%以上，且两者相差较大，表明该模型效果较差。回归模型有效，但效果差表明该模型需要改进，否则不能接受。

(2)图4为该回归方程模型，其中Ⅰ、Ⅱ、Ⅲ、Ⅳ温区温度方差膨胀因子数值明显较大，表明它们之间存在多重共线性关系[6]，即它们之间存在相互影响。对于该回归模型，我们要求数据的独立性，即数据之间不能互相影响，而图4中分析则表明4个温区温度并不独立。

(3)回归模型有效，但效果差的可能原因：①模型影响因子不全。本文只是提供一种研究方法，并没有就所有影响因子进行全方位研究。②本文因子数据因实际生产参数选择问题，并不能全部均匀连续取值，且每个因子取值域宽比例不一致，导致部分数值段数据量不足。

图3 回归模型因子方差分析

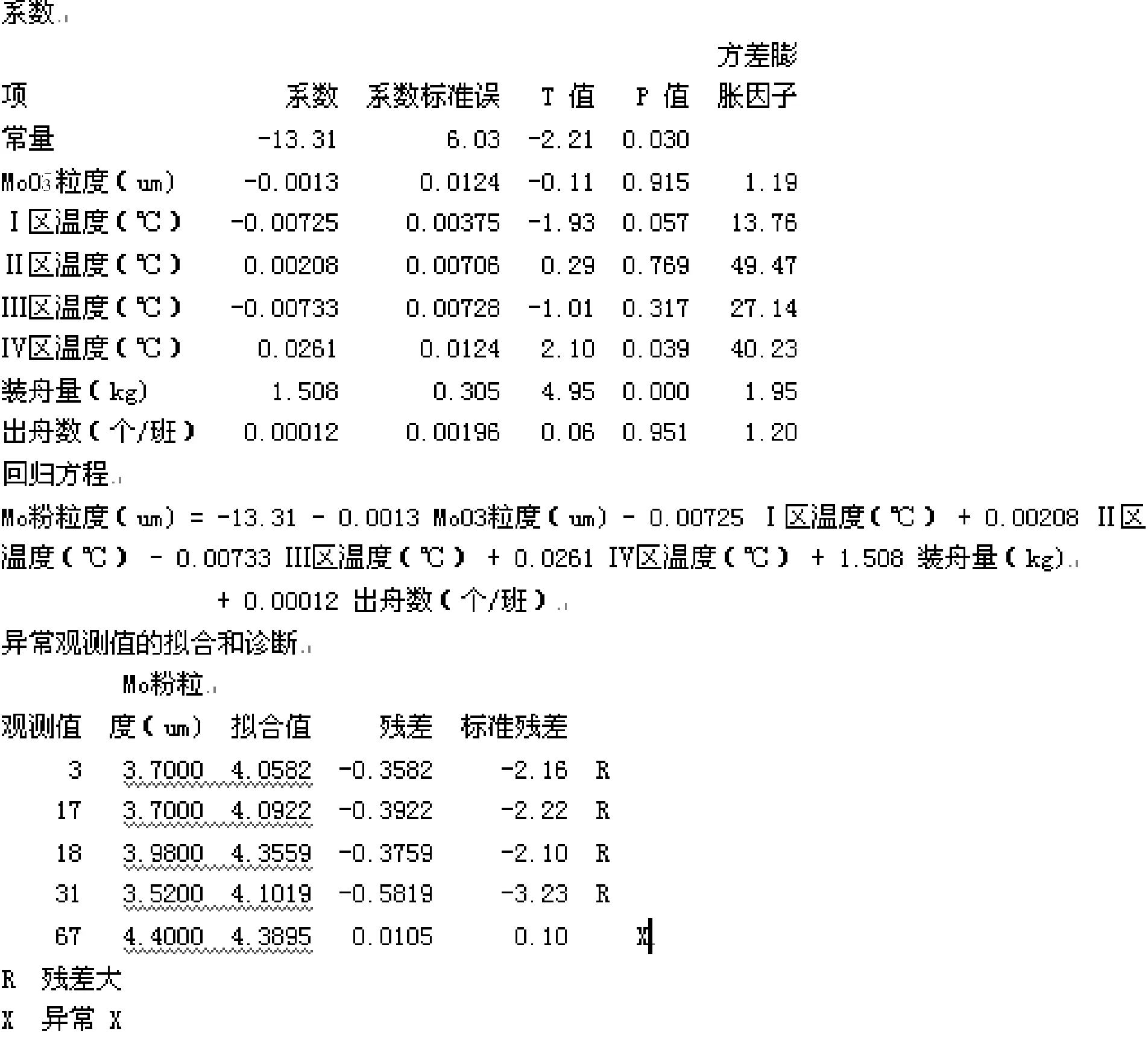
图4 多元回归方程及分析

3.2.3 残差检验分析

鉴于上述结论基本对模型进行了初步判断，但为了便于进一步对模型进行修改，我们可进行残差分析，证实模型的假定。用残差图诊断回归效果与样本数据的质量，检查模型是否满足基本假定，见图5。

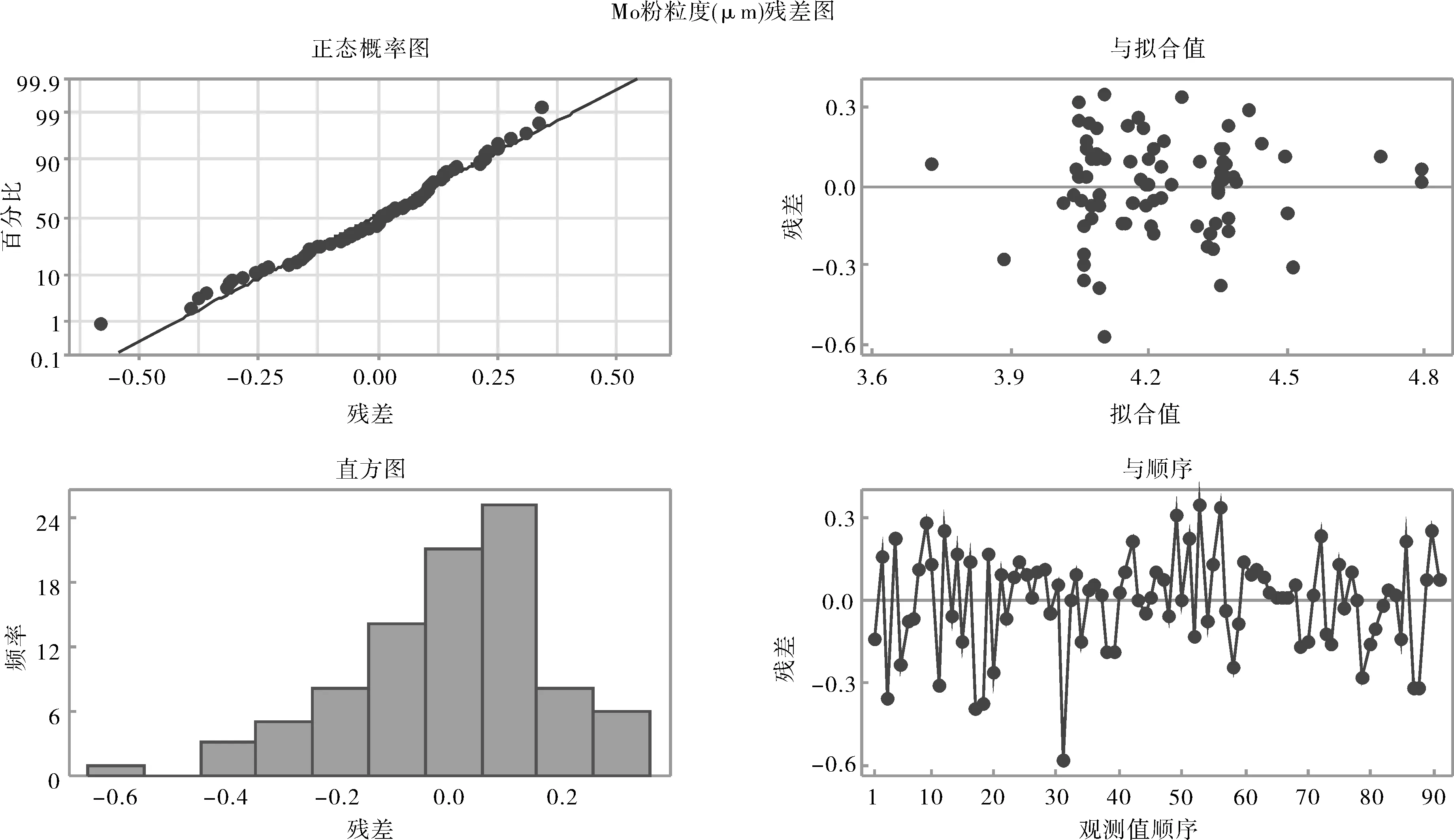
图5 残差四合一图

图5中左上图基本能直观判断样本数据残差项呈正态分布，说明所取数据符合模型对数据的正态分布要求，同时表明误差项也应符合正态分布这一假定；右上图表明样本观测值与模型预测拟合值的残差不存在明显弯曲或趋势，基本呈上下对称分布，而下面2幅图也表明观测值顺序对残差基本无影响。结合图3、图4的分析，我们可以判定本文建立的模型有效，只是模型预测效果较差，需要改进。

4 结 论

(1)MoO3粒度、二段还原Ⅰ、Ⅱ、Ⅲ、Ⅳ温区温度、装舟量及出舟数等7个影响因子均与钼粉粒度存在线性相关关系，K含量与钼粉粒度不存在明显线性相关关系。

(2)7个相关因子中，装舟量与钼粉粒度相关关系最强；其次4个温区温度的皮尔森系数大小接近且较装舟量小，次之；出舟数、MoO3粒度数值接近，最弱；以上影响因子中，装舟量、温度与钼粉粒度存在较强或强相关关系，而出舟数、MoO3粒度与钼粉粒度为弱相关关系。

(3)多元回归方程模型有效，其中Ⅳ区温度、装舟量因子对模型贡献显著，但模型效果及预测差。

(4)多元回归模型有效但效果差的原因：①模型影响因子不全。因篇幅及条件所限，本文只是提供一种研究方法，并没有就所有可能影响因子进行全方位研究。②生产条件所限，因子数据取值不均匀，部分段取值少甚至没有取值。

(5)在实际钼粉生产过程中，我们可以根据各因子与钼粉粒度之间的影响关系强弱进行工艺参数的优化。

(6)在条件允许或取值均匀连续情况下，本文的研究方法有效、可用。其也可应用于各类深加工产品的数据分析研究。

[1] 李洪桂.稀有金属学[M].北京：冶金工业出版社，1990.

[2] 稀有金属应用编写组.稀有金属应用(上册)[M].北京：冶金工业出版社,1985.

[3] 刘仁智，安 耿，李 晶，等.不同粒度钼粉对板材组织的影响[J].中国钼业，2006,30(1)：31-34.

[4] 刘宏亮，刘仁智，王培华.钼粉粒度及K含量的影响因素研究[J].中国钨业， 2015，30(3)：32-37.

[5] 中国质量协会组织.六西格玛管理(第3版)[M].北京：中国人民大学出版社,2014.

[6] 何晓群，刘文卿.应用回归分析(第3版)[M].北京：中国人民大学出版社，2011.

[7] 贾俊平,何晓群,金勇进.统计学(第6版)[M].北京：中国人民大学出版社，2015.

USING MULTIPLE REGRESSION ANALYSIS FOR THE INFLUENCING FACTORS OF MOLYBDENUM POWDER PARTICLE SIZE

CHENG Jin，XIAO Jiang-tao

(Metal Branch，Jinduicheng Molybdenum Co., Ltd., Xi′an 710077,Shaanxi,China)

By using the probability and statistical methods and related SPC tools, the factors affecting the particle size of molybdenum powder were analyzed and multiple regression analysis was conducted.Whether the main factors are related to the grain size of molybdenum powder and the significance level of influence were found out, and the applicable multivariate linear regression equation was obtained.Therefore, a more effective control method for molybdenum powder preparation was provided.

particle size; temperature; loading capacity; beat; K; multiple regression analysis; residual

2017-03-21；

2017-04-26

程 进(1982—)，男，冶金工程师，主要从事钼金属材料的研究。E-mail：halaywhy8@163.com

10.13384/j.cnki.cmi.1006-2602.2017.04.010

TG146.4+12

A

1006-2602(2017)04-0049-04