典型控制规律滑翔飞行器的轨迹预测方法*
2017-09-03张洪波黄景帅李广华汤国建
张洪波,黄景帅,李广华,2,汤国建
(1.国防科技大学 航天科学与工程学院,湖南 长沙 410073;2.空军航空大学 飞行器与动力系,吉林 长春 130022)
典型控制规律滑翔飞行器的轨迹预测方法*
张洪波1,黄景帅1,李广华1,2,汤国建1
(1.国防科技大学 航天科学与工程学院,湖南 长沙 410073;2.空军航空大学 飞行器与动力系,吉林 长春 130022)
针对临近空间高超声速滑翔飞行器机动能力强、轨迹灵活多变的特点,提出了一种基于典型控制规律的高超声速滑翔飞行器轨迹预测方法。在前期先验信息的基础上,将典型控制规律下的控制参数——攻角和倾侧角建模成一阶Gauss- Markov过程,联合飞行器在半速度坐标系下的运动微分方程组成扩展的状态变量,选择飞行器的经纬高与速度大小作为无迹卡尔曼滤波的观测量并对控制参数进行滤波辨识,结合控制参数的辨识值重构其规律,进而预测飞行器的轨迹。通过仿真分析了对跳跃和非跳跃2种典型飞行轨迹的预报效果,结果表明所提方法对倾侧角不翻转的情况具有良好的预测精度。
高超声速滑翔飞行器;典型控制规律;Gauss- Markov过程;参数辨识;无迹卡尔曼滤波;轨迹预测
0 引言
临近空间高超声速滑翔飞行器(hypersonic glide vehicle,HGV)是一类飞行马赫数大于5,依靠气动升力在临近空间内实现长时间远距离飞行的飞行器。它既可由空间轨道释放再入,也可由助推火箭从地面发射到指定高度后再入[1]。HGV突破了常规弹道式弹头的再入模式,具备超远程、持续机动和快速到达的能力,给现有的防空反导系统带来了极大的挑战,因此受到了广泛的关注。目前,典型的试验型号有美国的HTV- 2(hypersonic technology vehicle- 2)和AHW(advanced hypersonic weapon)[2]。
由于HGV飞行速度快,通常只能采用迎面拦截的策略,导引速度较低的拦截器去接近HGV。迎面拦截需要通过精确预测HGV的飞行轨迹来获取预测命中点,降低拦截弹在中制导飞向预测命中点过程中修正偏差的能量消耗,创造良好的中末制导交班条件。然而,HGV的持续机动能力使其无固定飞行轨迹,难以预知未来机动时刻,导致预测模型建立不准确,预测精度较低。虽然对于防御方而言,HGV的控制规律是未知的,但是由于在整个飞行过程中受过载、动压和驻点热流等约束的限制,控制参数一般会遵循一定的规律,特别是攻角的复杂变化对HGV的姿态控制是不利的,这给HGV的轨迹预测带来了可能[3]。文献[4]探讨了非惯性弹道预报的技术可行性,给出了解析法、数值积分法和函数逼近法3种弹道外推预报方法。文献[5]通过分析与弹道导弹目标弹道预测的差异,提出了基于弹道规划设计、滤波理论和几何理论的3种高超声速飞行器弹道预测方法。文献[4-5]仅仅是提供了对HGV轨迹预测的思路,并没涉及具体实现。目前,针对HGV轨迹预测的方法主要分为基于动力学或运动学模型两大类。基于动力学模型的方法通常先通过跟踪估计出气动参数、升阻比或控制参数的变化趋势,然后研究其变化规律或借助函数拟合工具给出未来时刻的变化趋势,进而代入动力学模型进行轨迹预测,该方法一般需要HGV的部分先验信息,在无先验信息的条件下实现难度较大[6-8]。基于运动学模型的方法通常先通过跟踪估计出加速度的变化趋势,然后利用函数拟合或选择最佳机动模型给出未来时刻的变化趋势,进而代入运动学模型进行轨迹预测,该方法一般不需要HGV的先验信息,但可能需要目标的持续跟踪信息[3,9]。与传统基于动力学或运动学模型的方法不同,文献[10]以广义回归神经网络GRNN(generalized regression neural network)理论为依据,提出了一种基于误差修正的GRNN高超声速飞行器轨迹预测方法,给轨迹预测研究提供了一种新思路。由于对HGV轨迹预测的研究刚刚起步加之HGV轨迹多变,上述所提方法均处于探索阶段,存在模型建模不准、预报精度低或适用性差的缺点,仍需不断深入地研究。
鉴于HGV在滑翔阶段飞行时间长,留给拦截系统的反应时间相对充裕,拦截概率高[11],本文因此针对HGV的滑翔段进行了轨迹预测的研究。首先根据前期对HGV运动状态的跟踪滤波结果,对典型控制规律下HGV的控制参数进行辨识,通过对控制参数的重构进行轨迹预测,为研究高精度高可靠性的HGV轨迹预测方法提供了理论基础与方向导引。
1 飞行走廊建模
1.1 约束条件
HGV在飞行过程中受诸多复杂约束条件的影响,主要包括热流密度、动压、过载、控制量、航路点、禁飞区等过程约束及起点、终端等端点约束,复杂的约束条件将相应地对HGV的飞行轨迹产生不同程度的运动限制。本文主要研究过程约束中热流密度、动压和过载约束对HGV飞行轨迹的影响。
(1)
式中:Kn表示常数,与飞行器的头部半径和材料有关;g0=9.806 65 m/s2,为海平面地球引力加速度。考虑到飞行器的控制能力,为了限制其弹道发生跳跃,一般会增加零倾侧角平衡滑翔约束条件,即
(2)
在实际应用中认为θ是小量,cosθ≈1。
1.2 飞行走廊数学描述
飞行器安全飞行时所满足的约束条件的交集称为飞行走廊。通常情况下,对飞行走廊在飞行剖面中进行描述,主要包括动压-速度(q-v)、阻力加速度-速度(D-v)、高度-速度(H-v)、阻力加速度-能量(D-E)等剖面,这里采用在阻力加速度-速度剖面内建立飞行走廊数学模型,其余类似。
将式(1),(2)中各表达式转换为阻力加速度和速度的函数表达式,得
(3)
从而,可得到D-v剖面内的飞行走廊上下边界为
(4)
文献[3]通过仿真得到了D-v剖面内飞行走廊的上下边界,发现HGV在初始再入阶段热流密度约束起决定作用,随着飞行速度的降低其不再起决定作用。
2 典型控制规律下的控制参数辨识
2.1 控制参数建模
虽然HGV具有持续机动能力,轨迹灵活多变,但是受到各种约束和自身控制能力的限制,在实际HGV的轨迹设计与制导中,控制参数的变化规律会选择得尽可能简单。为满足热流密度约束和射程能力的需要,攻角一般选择为速度的分段线性函数。在标准轨迹制导中,倾侧角通常在初始再入段时采用常值,滑翔段时采用方位角误差走廊进行符号的翻转控制,大小由飞行剖面确定[3]。经过大量的仿真计算验证,该制导规律下的倾侧角符号在不翻转时近似为时间的线性函数。在预测校正制导中,为了迭代的方便,倾侧角也均采用简单的线性或分段线性函数来描述[1]。
由于控制参数的变化趋势并不复杂,根据一般参数辨识的方法,可将攻角和倾侧角建模成一阶Gauss- Markov过程[12]。即
(5)
式中:εα和εν为高斯白噪声。
2.2 控制参数辨识
结合HGV在半速度坐标系下的运动方程[1,13],将控制参数与其中的6个状态变量组成新的扩展状态变量,表示为
(6)
其对应的微分方程为
(7)
很明显,式(7)具有强耦合性和强非线性,特别是攻角隐含在升力中,对其进行线性化将非常繁琐,因此采用无迹卡尔曼滤波(unscented Kalman filter,UKF)[14]对控制参数进行辨识,即
(8)
式中:T为采样时间;wk为系统过程噪声,其协方差矩阵为Qk。
由地面雷达前期的观测数据,利用非线性滤波的理论可估计出HGV在地面雷达坐标系中的位置和速度。为了与式(6)中的变量统一,需将估计出的位置信息转换为纬度、经度和地心距的形式。联合估计出的速度,选择该4个变量作为控制参数辨识滤波的观测量,即
(9)
因此,系统的观测方程为
(10)
式中:
υk为观测噪声。
在HGV的跟踪滤波中,状态变量X′的前6个分量通常为位置和速度在地面雷达坐标系下的分量。因此,υk对应的协方差矩阵Dk可通过X′估计误差的协方差矩阵P中的元素进行求解得到。这里假设速度与其他3个量是不相关的,则速度对应的方差也即Dk的第1个元素为

(11)

(12)
式中:x,y,z分别为HGV在地心坐标系下的位置分量。因此,Dk的表达式为
(13)
3 基于典型控制规律的轨迹预测
若假设HGV飞行过程中根据其发射位置、光电特性、弹道特性等方面的信息对飞行器进行了有效识别,并通过前期情报搜集和飞行器反设计,已获得飞行器的本体参数。从理论上讲可对典型控制规律下的HGV进行轨迹预测,预测的流程可用图1进行表示。

图1 基于典型控制规律的轨迹预测流程图Fig.1 Flow chart of trajectory prediction based on typical control law
图1中首先是利用地面雷达对HGV进行轨迹跟踪,将位置的跟踪结果转换成经纬高形式。对典型控制规律下的控制参数进行建模,将其扩展到半速度坐标系下HGV运动方程的状态变量中,并对扩展变量进行滤波,进而辨识控制参数。然后对控制规律进行重构,得到控制参数的具体规律,最后对轨迹进行预测。图1中虚横线区域表示验前信息,表示工作要在跟踪预测前完成,是采用该预测方法的前提,在本文中假设该部分已经完成。图1中虚点线区域表示控制参数辨识部分,是轨迹预测方法的关键。
4 仿真校验
为了验证不同轨迹及不同控制参数输入条件下的轨迹预测效果,本文基于CAV-H的数据设计了2条典型的HGV轨迹。一条是跳跃轨迹,仅受攻角控制生成,倾侧角为0,攻角为速度的分段线性连续函数;另一条是非跳跃轨迹,由攻角和倾侧角联合控制生成,攻角变化规律与跳跃轨迹相同,并设计了满足过程和端点约束的D- v的飞行剖面。HGV跟踪D- v剖面飞行,倾侧角大小由D- v剖面确定,其符号翻转由方位角误差走廊控制。
设地面雷达距离观测噪声的标准差为10m,角度观测噪声的标准差为10-3rad。飞行器跟踪采用基于气动参数的扩展卡尔曼滤波(extendeddKalmanfilter,EKF)跟踪算法[3,15],并将跟踪结果作为控制参数辨识的观测量。
4.1 跳跃轨迹预测
地面雷达的纬度和经度坐标为(1.5°,38°),设计的HGV跳跃轨迹及通过地面部署的雷达可观测的轨迹弧段如图2所示。

图2 跳跃轨迹及可观测弧段Fig.2 Skipping trajectory and observable arc segment
取过程噪声的协方差阵为Qk=diag(10-16,10-16,10-16,10-16,10-16,10-16,10-10,10-10)。图3,4给出了控制参数辨识滤波后的结果。从图3可看出,前期攻角辨识的误差接近于2o,后期攻角辨识的误差小于0.5o;图4表明倾侧角辨识的精度较高,基本接近于0。一般条件下,在飞行过程中,若有倾侧角参与控制,其值不会接近于0,所以轨迹预测过程中可认为倾侧角为0。

图3 跳跃轨迹攻角辨识结果Fig.3 Angle of attack identification result of skipping trajectory

图4 跳跃轨迹倾侧角辨识误差Fig.4 Angle of bank identification error of skipping trajectory
在轨迹预测过程中,指定1 000s为预测起始时刻。考虑到辨识滤波的收敛时间,选取700~1 000s内(辨识滤波稳定后)的辨识结果对攻角和倾侧角进行重构。认为攻角是时间的线性函数,倾侧角则认为是0。根据重构后的攻角表达式对1 000s后的攻角进行预测,攻角的预测结果如图5所示,可看出攻角的预测精度优于1°。以1 000s处HGV状态变量的滤波值为预测初值,在预测的攻角作用下进行轨迹递推预测,由此得到的HGV轨迹预测结果如图6所示,其中预测精度在km量级,可满足后续任务的需要。
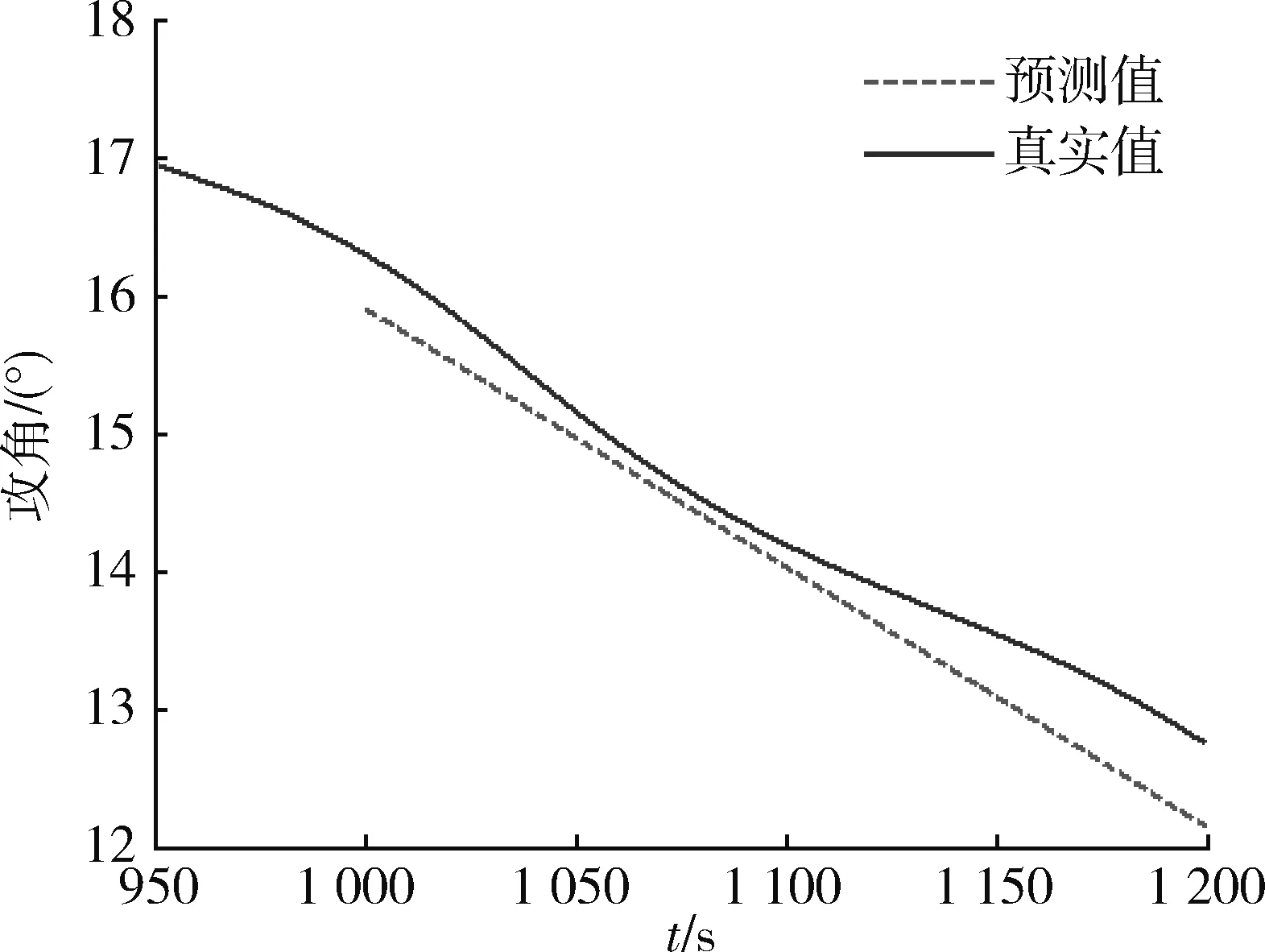
图5 跳跃轨迹攻角预测结果Fig.5 Angle of attack prediction result of skipping trajectory

图6 跳跃轨迹预测结果Fig.6 Prediction result of skipping trajectory
4.2 非跳跃轨迹预测
地面雷达的纬度和经度坐标为(2°,45°),设计的HGV非跳跃轨迹及通过地面部署的雷达可观测的轨迹弧段如图7所示。

图7 非跳跃轨迹及可观测弧段Fig.7 No- skipping trajectory and observable arc segment

图8 非跳跃轨迹攻角辨识结果Fig.8 Angle of attack identification result of no- skipping trajectory
取过程噪声的协方差阵为Qk=diag(10-12,10-10,10-10,10-10,10-10,10-10,10-8,10-18)。图8,9给出了控制参数辨识滤波后的结果。从2图中可看出,与真实值相比,辨识值能够表征真实值的变化规律,精度较高。
在轨迹预测过程中,指定900s为预测起始时刻。选取800~900s内(辨识滤波稳定后)的辨识结果对攻角和倾侧角进行重构,认为攻角和倾侧角均是时间的线性函数。根据重构后的控制参数表达式对900s后的控制参数值进行预测,攻角和倾侧角的预测结果分别如图10,11所示。这里假设已知HGV飞行后期是以最大升阻比攻角进行飞行,因此当预测攻角小于11°(最大升阻比攻角)时,将其截断为11°。由于该方法无法预知倾侧角的翻转时刻,因此预测的倾侧角在其翻转后误差较大。

图9 非跳跃轨迹倾侧角辨识结果Fig.9 Angle of bank identification result of no- skipping trajectory

图10 非跳跃轨迹攻角预测结果Fig.10 Angle of attack prediction result of no- skipping trajectory
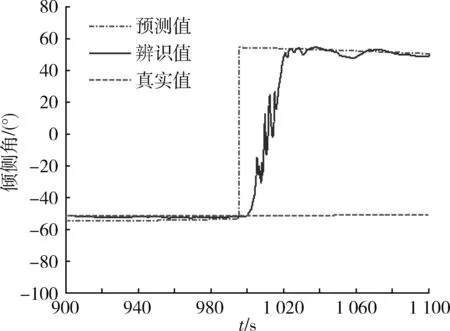
图11 非跳跃轨迹倾侧角预测结果Fig.11 Angle of bank prediction result of no- skipping trajectory
以900s处HGV状态变量的滤波值为预测初值,在预测的攻角和倾侧角作用下进行轨迹递推预测,由此得到的HGV轨迹预测结果如图12所示。可以看出,在倾侧角翻转点前预测的轨迹几乎与真实轨迹重合。由于该方法无法预知倾侧角的翻转时刻,在真实倾侧角翻转后,而轨迹预测中仍按照重构得到的倾侧角对HGV的轨迹进行预测,因此预测的轨迹在倾侧角翻转后与HGV真实轨迹相差甚远。
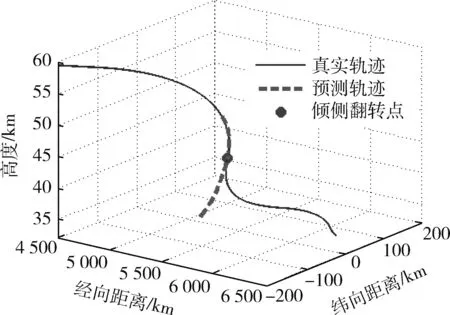
图12 非跳跃轨迹预测结果Fig.12 Prediction result of no- skipping trajectory
5 结束语
针对高超声速滑翔飞行器滑翔段的轨迹预测问题,本文提出了一种基于典型控制规律的高超声速滑翔飞行器轨迹预测方法。该方法利用前期地面雷达跟踪滤波的结果作为控制参数辨识滤波的观测量来辨识控制参数的变化规律,并对其进行重构,进而进行轨迹预测。通过预测跳跃轨迹和非跳跃轨迹的仿真,验证了本方法对倾侧角不翻转的情况具有良好的轨迹预测精度。当真实轨迹中存在倾侧角翻转时,由于本方法目前还无法预知其翻转时刻,导致翻转后的轨迹预测精度较差,具有一定的局限性,有待在后续的研究工作中加以改进与完善。
[1] 谢愈.复杂约束条件下高超声速滑翔飞行器弹道规划方法研究[D].长沙:国防科技大学,2012.XIEYu.StudyofTrajectoryPlanningApproachwithComplicatedConstraintsforHypersonicGlideVehicles[D].Changsha:NationalUniversityofDefenseTechnology,2012.
[2] 梁晓庚,田宏亮.临近空间高超声速飞行器发展现状及其防御问题分析[J].航空兵器,2016(4):3-10.LIANGXiao-geng,TIANHong-liang.AnalysisoftheDevelopmentStatusandtheDefenseProblemofNearSpaceHypersonicVehicle[J].AeroWeaponry,2016(4):3-10.
[3] 李广华.高超声速滑翔飞行器运动特性分析及弹道跟踪预报方法研究[D].长沙:国防科技大学,2016.LIGuang-hua.MotionCharacteristicsAnalysisandTrajectoryPredictionforHypersonicGlideVehicles[D].Changsha:NationalUniversityofDefenseTechnology,2016.
[4] 张洪波,谢愈,陈克俊,等.非惯性运动目标弹道预报技术探讨[J].现代防御技术,2011,39(6):26-31.ZHANGHong-bo,XIEYu,CHENKe-jun,etal.InvestigationonTrajectoryPredictionofManeuverableTarget[J].ModernDefenceTechnology,2011,39(6):26-31.
[5] 韩春耀,熊家军.高超声速飞行器弹道预测方法研究[J].飞航导弹,2016(2):24-27.HANChun-yao,XIONGJia-jun.ResearchontheTrajectoryPredictionMethodforHypersonicVehicles[J].AerodynamicMissileJournal,2016(2):24-27.
[6] 秦雷,李君龙,周荻.临近空间非弹道式目标HTV- 2跟踪滤波与预报问题[J].航天控制,2015,33(2):56-61.QINLei,LIJun-long,ZHOUDi.TheProblemsofTrackingFilterandPredictionforNon-BallisticTargetHTV- 2intheNearSpace[J].AerospaceControl,2015,33(2):56-61.
[7] 王路,邢清华,毛艺帆.助推-滑翔无动力跳跃飞行器轨迹预测[J].空军工程大学学报,2015,16(1):24-27.WANGLu,XINGQing-hua,MAOYi-fan.ATrackForecastingAlgorithmofBoost-GlideUnpropulsiveSkippingVehicle[J].JournalofAirForceEngineeringUniversity,2015,16(1):24-27.
[8] 王路,邢清华,毛艺帆.基于升阻比变化规律的再入高超声速滑翔飞行器轨迹预测算法[J].系统工程与电子技术,2015,37(10):2335-2340.
WANG Lu,XING Qing- hua,MAO Yi- fan.Trajectory Prediction of Reentry Hypersonic Glide Vehicle Based on Changing Rule of Lift- Drag Ratios[J].Systems Engineering and Electronics,2015,37(10):2335-2340.
[9] 魏喜庆,王社阳,李瑞康.基于自适应IMM算法的高超声速飞行器轨迹预测[J].上海航天,2016,33(2):27-31. WEI Xi- qing,WANG She- yang,LI Rui- kang.Trajectory Predicting of Hypersonic Vehicle Using Adaptive Interactive Multiple Model Filter[J].Aerospace Shanghai,2016,33(2):27-31.
[10] 杨彬,贺正洪.一种GRNN神经网络的高超声速飞行器轨迹预测方法[J].计算机应用与软件,2015,32(7):239-243. YANG Bin,HE Zheng- hong.Hypersonic Vehicle Track Prediction Based on GRNN[J].Computer Applications and Software,2015,32(7):239-243.
[11] 呼卫军,周军.临近空间飞行器拦截策略与拦截武器能力分析[J].现代防御技术,2012,40(1):11-15. HU Wei- jun,ZHOU Jun.Analysis of the Interception Strategy of the Near Space Vehicle and Capability of the Interception Weapon[J].Modern Defence Technology,2012,40(1):11-15.
[12] 崔乃刚,卢宝刚,傅瑜,等.基于卡尔曼滤波的再入飞行器气动参数辨识[J].中国惯性技术学报,2014,22(6):755-758. CUI Nai- gang,LU Bao- gang,FU Yu,et al.Aerodynamic Parameter Identification of a Reentry Vehicle Based on Kalman Filter Method[J].Journal of Chinese Inertial Technology,2014,22(6):755-758.
[13] 赵汉元.飞行器再入动力学与制导[M].长沙:国防科技大学出版社,1997. ZHAO Han- yuan.Dynamics and Guidance for Flight Vehicle Entry[M].Changsha:National University of Defense Technology Press,1997.
[14] SIMON D.最优状态估计—卡尔曼,H∞及非线性滤波[M].张勇刚,李宁,奔粤阳,等,译.北京:国防工业出版社,2015. SIMON D.Optimal State Estimation:Kalman,H∞,and Nonlinear Approaches[M].ZHANG Yong- gang,LI Ning,BEN Yue- yang,et al,Translated.Beijing:National Defense Industry Press,2015.
[15] 夏佩伦.目标跟踪与信息融合[M].北京:国防工业出版社,2010. XIA Pei- lun.Target Tracking and Information Fusion[M].Beijing:National Defense Industry Press,2010.
Trajectory Prediction of Glide Vehicle Based on Typical Control Law
ZHANG Hong- bo1,HUANG Jing- shuai1,LI Guang- hua2,TANG Guo- jian1
(1.National University of Defense Technology,College of Aerospace and Engineering,Hunan Changsha 410073,China; 2.Air Force Aviation University,Flight Vehicle and Dynamic Department,Jilin Changchun 130022,China)
Aiming at the features of high maneuverability and trajectory flexibility, a trajectory prediction method for hypersonic glide vehicle (HGV) is proposed based on the typical control law. On the foundation of the priori information, the control parameters- angles of attack and bank are considered as the first order Gauss- Markov process. The extended state variables are constructed by means of combining with the kinematic differential equations of HGV described in the half- speed coordinate system. The filtering results of HGV position tracking after the longitude- latitude- altitude transformation and velocity are chosen as the measurements, and the unscented Kalman filter (UKF) is used to identify the control parameters. According to the identified values, the constructed control law can be obtained and the HGV trajectory can be predicted. The results of simulating and analyzing the two typical flight trajectories of skipping and no- skipping demonstrate that the proposed method can acquire the satisfactory prediction accuracy at the absence of the turnover of bank angle.
hypersonic glide vehicle (HGV); typical control law; Gauss- Markov process; parameter identification; unscented Kalman filter (UKF); trajectory prediction
2016-10-20;
2017-02-14 作者简介:张洪波(1981-),男,山东济阳人。副教授,博士,主要从事飞行器动力学与控制方面的研究工作。
10.3969/j.issn.1009- 086x.2017.04.018
V412.4
A
1009- 086X(2017)- 04- 0112- 07
通信地址:410073 湖南省长沙市国防科技大学航天科学与工程学院 E- mail:zhanghb1304@nudt.edu.cn
