二元正交chirp载波水声通信时变多普勒系数估计

李增祥，刘磊，赵云江，刘凇佐

(1.山东理工大学 计算机科学与技术学院，山东 淄博 255000； 2.哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨150001)

二元正交chirp载波水声通信时变多普勒系数估计

李增祥1，刘磊2，赵云江2，刘凇佐2

(1.山东理工大学 计算机科学与技术学院，山东 淄博 255000； 2.哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨150001)

针对水下潜器间相对变速运动时进行声通信导致的宽带多普勒和码元间多普勒不一致的问题，本文提出一种基于二元chirp信号的移动稳健水声通信系统的多普勒估计和解调算法。基于分数阶傅里叶变换(FRFT)对同步信号处理得到初始多普勒系数后，利用相邻码元间的相关性，对相邻码元进行滑动匹配迭代处理，实现对每一个chirp载波的多普勒系数估计，同时在估计多普勒系数的过程中利用中间变量实现对信号的解调。海上通信距离5 km，运动速度为1.5 m/s时,可以达到误码率小于10-4的通信效果。仿真和海上试验结果都证实了该方法的有效性。

线性调频信号；移动水声通信；分数阶傅立叶变换；多普勒系数估计；滑动匹配；信号处理；时变信号

伴随着人们对海洋开发和探索的逐渐深入，各种水下潜器在海洋勘探开发领域发挥越来越大的作用，特别是编队协同工作时，需要利用水声通信技术进行信息沟通[1]。由于海水强烈的吸收特性，基于无线电的通信方式无法直接应用于水下的远程通信。声波是迄今为止唯一可以进行水下远程信息传输的载体。因而水声通信占据着水下无线信息传输领域的主导地位。本文基于具有大多普勒容限的chirp信号[2]，研究适用于水下潜器的稳健移动水声通信技术，具有广泛的需求，对提高水下潜器作业的安全性、有效性和工作效率具有重要的意义。

当前，国内外关于水声通信的研究主要面向点对点近距离高速、远距离稳健、语音通信等领域，并不适用于水下潜器移动时稳健水声通信的需求。水声通信是典型的宽带通信[3]，其多普勒效应比陆地无线通信更加严重，导致应用在陆地无线通信中许多成熟的多普勒估计方法无法直接应用于水声通信。因此，在水声移动通信中，为了保证通信系统的正常工作，准确地实现多普勒因子的估计显得尤为重要。对于水声通信中的多普勒估计问题，国内外有关学者进行了大量研究，可以归纳为两类：1)测量接收信号的频率，通过频率的偏移量来对多普勒系数进行估计[4]；2)根据多普勒效应引发的时域展宽或压缩的效应，通过测量信号的时域展宽或者压缩量进行多普勒系数的估计[5]，其中比较典型的方法是文献[6]中所提到的两种的方法，即模糊度函数方法与块多普勒估计方法。也有学者将一些新的信号处理技术引入水声通信来进行多普勒估计，如基于分数阶傅里叶变换的估计方法[7]、基于部分傅里叶变换的间接方法[8]等。文献[9]提出了基于频域变采样的OFDM 水声移动通信多普勒补偿算法，文献[10]提出了水声扩频通信多普勒估计与补偿方法，但此方法的实现过程不具有一般性。以上方法一般都只是适用于静止水声通信的多普勒估计，而移动水声通信中的多普勒因子具有动态时变特性，这些方法往往不能正确估计出每个码元的多普勒因子，而且当多普勒因子较大时，估计精度也不高，并不适用于高速时变移动条件下的水声通信。

针对上述问题，本文基于具有大多普勒容限的chirp信号，提出了一种滑动匹配迭代多普勒系数估计方法，这种方法不仅能对每个码元的多普勒系数进行精确地估计，并且能够在估计多普勒系数的同时对信号进行准确的解调，实现了多普勒补偿和数据解调同时进行。

1 水声通信中的多普勒效应

水声通信频带较低，中心频率与带宽在同一个数量级上，属于宽带调制方式，其多普勒效应不仅会产生频率的偏移，还会引起时域波形的压缩和扩展，所以在水声通信中多普勒效应由式(1)表达更为准确：

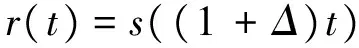
(1)

式中：r(t)为接收信号，s(t)发送信号，Δ为相对多普勒系数，根据速度的计算方法如公式(2)所示

(2)

式中：vs为发送端径向速度，vr为接收端径向速度，c为水中声速，Δ为相对多普勒频移。根据载波频率的计算方法如公式(3)所示。

(3)

式中：fr为发射信号的载波频率，fs为接收信号的载波频率，fd为频率偏移。

如果信号是离散的，则式(1)可表示为：

(4)

式中：n为整数，Ts是采样时间。式(4)可以等效为采样时间的压缩和展宽。因此可以通过改变采样时间，也就是调整采样频率对接收信号重采样来进行多普勒补偿，恢复原信号，如公式(5)所示。新的采样率可以表示为公式(6)

(5)

(6)

式中：D为压缩扩展系数，因此只有对多普勒补偿因子Δ进行估计，才能进行有效的多普勒补偿，然后根据估计值对接收的数据进行重采样。所以传统水声通信中的多普勒补偿可分为两个步骤：1)多普勒因子估计，2)根据估计出的补偿因子对接收数据进行重采样，流程图为图1所示。

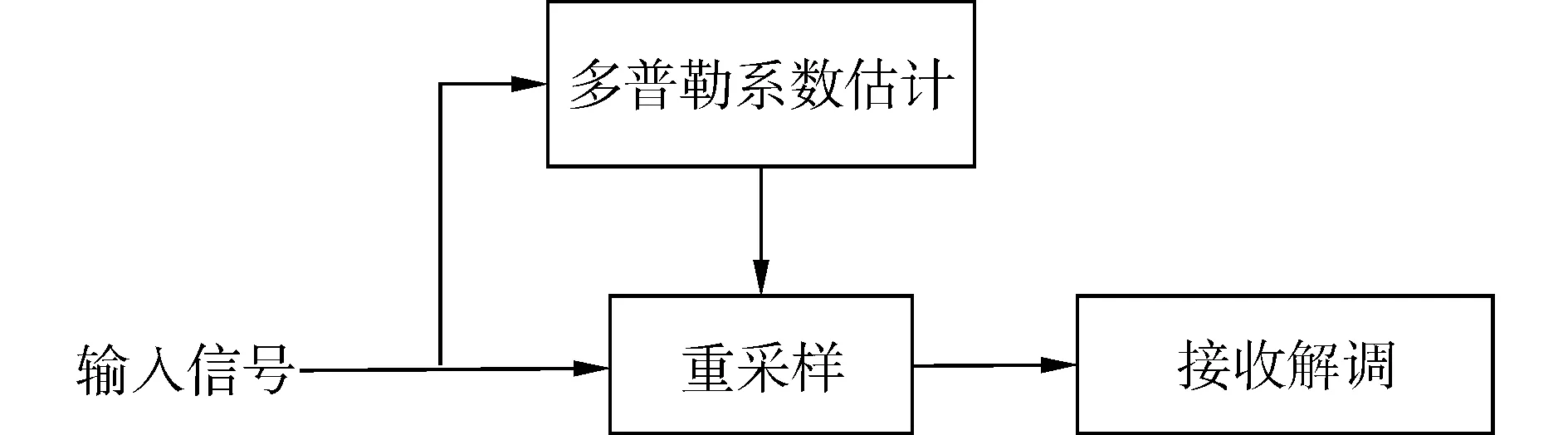
图1 多普勒补偿流程图Fig.1 Doppler compensation flow chart

2 CSSBOK水声通信多普勒系数估计与补偿

2.1 CSSBOK水声通信

本文基于二元正交chirp载波调制算法(chirp spread spectrum binary orthogonal keying，CSSBOK)研究多普勒估计方法。CSSBOK调制方式利用chirp信号的正负调频斜率来传输二进制数据信息的调制方式[11]，两种chirp的信号具有相同的时间宽度和起止频率，但调频率互为相反数，为±u，图2为CSSBOK调制系统的原理框图。

线性调频信号(linear frequency modulation，LFM)也称为chirp信号，线性调频信号因为具有良好的自相关特性，而且不容易受到噪声干扰的影响，所以成为了在水声通信中使用最广泛的一种信号。在发送端，chirp上调频信号和下调频信号作为载波传递二进制码元信息，将调制好的信号送入信道中进行传输，在信道中信号受到噪声以及多途的干扰。接收端分两路对接收到的信号进行匹配滤波，一路送到chirp上调频匹配滤波器，另外一路送到chirp下调频匹配滤波器。如果接收到的信号与chirp上调频匹配滤波器的冲激响应匹配，那么就会产生很大的脉冲压缩，此时的信号与chirp下调频匹配滤波器则因为不匹配而产生能量均匀分布的噪声带，后对两路匹配滤波器的输出结果的幅度进行抽样判决。chirp信号的一般表达式为c(t)=Acos(2πf0t+πut2),-T/2≤t≤T/2

(7)

其瞬时相位和瞬时频率表达式为

φ(t)=2πf0t+πut2

(8)

f(t)=f0+ut

(9)

式中：T是扫频时间，f0是起始频率，u是调频率，u的正负决定了线性调频信号瞬时变化的方向。u>0称为上调频信号，也叫up_chirp信号；反之，u<0称为下调频信号，也叫down_chirp信号。

图2 CSS_BOK调制解调系统框图Fig.2 CSS_BOK modulation system flow chart

chirp信号的最大特点就是利用匹配滤波可以在高斯白噪声信道下获得最佳的系统信噪比。匹配滤波器的冲激响应就是调频方向相反，其他参数相同的chirp信号。以上调频信号为例，与式(7)相对应的匹配滤波器的单位冲激响应如下

h(t)=Acos(2πf0t-πut2)，-T/2≤t≤T/2

(10)

经过匹配滤波器的up_chirp信号的输出如下

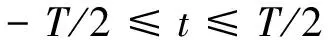
(11)

式中：B为带宽，在t=0时，g(t)取到最大值，t=±1/B处为其第一零点处。chirp上调频信号主瓣宽度为2/B，峰值为BT，经过匹配滤波后，其对应的匹配输出具有和sinc函数类似的特性，所以chirp信号的低峰值功率信号变成了一个能量集中于很短的时间内，具有高峰值功率的信号，这样的特性非常利于检测和捕获chirp信号。

2.2 分数阶傅里叶变换的多普勒系数估计与补偿

假设chirp信号受到多普勒效应的影响，根据式(7)～(9)，则在接收端受多普勒效应影响的chirp信号瞬时相位与频率为

(12)

式中：D=1+Δ。由式(11)和式(12)比较可得，多普勒效应给chirp信号带来的影响可分为3个方面，分别是chirp信号的时域压缩或展宽、初始频率由f0变为Df0、信号调频斜率由u变为D2u。

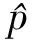
(13)

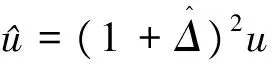
(14)

由于水中载体运动速度的限制，使得|Δ|远小于1，所以可认为1+Δ恒为正数，式(14)可化为

(15)

式(15)就是基于FRFT的多普勒系数估计的表达式。

在对基于FRFT的多普勒系数进行补偿时，首先通过同步信号估计出整帧信号的多普勒系数，然后对数据信号进行串并转换，并用估计出来的多普勒系数进行多普勒补偿，补偿后的信号在进行均衡消除多途干扰，最后进行判决，对信号进行解调。具体流程如图3所示。

图3 基于FRFT的多普勒补偿流程图Fig.3 Doppler compensation based on FRFT flow chart

2.3 改进的滑动匹配时变多普勒系数估计与补偿

图4 多普勒效应示意图Fig.4 Doppler effect diagram

取前N个采样点与后N个采样点对应的数值依次相乘并且求和取平均：

(16)

其中IMAX是多普勒系数估计采样点最大滑动范围，这样改变i的数值，得到一组Mi的值，由匹配相关的原

(17)

该值即为基于滑动匹配的多普勒系数估计的解析式，在实际情况下，发射机与接收机径向速度不可能恒定不变，因此在一段信号中不同码元信号所产生的多普勒频移值可能不同，就需要对每一段码元分别进行多普勒估计与补偿。由于基于FRFT的多普勒系数估计只能通过同步信号大致估计出所有码元的多普勒系数，并不能准确找出每个码元采样点的变化量，这样进行补偿会产生迭代的误差。而滑动匹配的方法却能做到这一点，滑动匹配可以先找出码元信息的前两个码元做匹配，估计出来的多普勒系数对第一个码元做补偿，再对第二第三个码元做匹配，依次类推，对每一个码元都能够进行较为精确的多普勒补偿，称之为滑动匹配跟踪算法。滑动窗长度的大小取决于该算法的多普勒容限。

同时在对信号进行多普勒补偿的同时也完成了对信号的解调，首先找到第一个码元所在的位置，并在多普勒补偿后用FRFT对其进行解调，在这里假设其为二进制数据“1”，若其能与第二个码元进行匹配，则第二个码元也为数据“1”，若不能进行匹配，则为数据“0”，在确定了第二个码元信息后，又可以对第三个码元进行解调，依次类推，就能完成对所有码元的解调。流程如图5所示。

图5 基于滑动匹配的多普勒补偿流程图Fig.5 Doppler compensation based on sliding matching flow chart

3 移动水声通信仿真与实验

为验证本方法性能，分别进行了仿真研究和海上试验。仿真和海上试验参数相同，采用CSSBOK调制方式，通信频带为8～12 kHz，码元宽度10 ms；每个码元携带1 bit信息，通信速率为100 bit/s。

3.1 仿真研究

本小节主要研究了基于FRFT的多普勒系数估计方法与滑动匹配的多普勒系数估计方法的性能，利用chirp信号进行多普勒系数估计，首先在无多途信道影响条件下，分析了基于滑动匹配的多普勒系数估计方法的实际性能。表1是基于FRFT的多普勒系数估计结果，表2是基于滑动匹配的多普勒系数估计结果，信道中的噪声为高斯白噪声。

结合表1、表2可知，随着信噪比的逐渐增加，多普勒系数的估计值逐步接近理论值，在高信噪比条件下，两种方法都能够看为近似无偏的估计，但显然在-5 dB信噪比以上与同一径向相对速度的情况下，基于FRFT的多普勒系数估计值比基于滑动匹配的估计值更接近理论值，在较高信噪比的条件下基于FRFT的多普勒系数的估计性能不会随着相对运动速度的变换而发生明显的变化，但基于滑动匹配的多普勒系数估计的性能显然在相对径向速度越小的情况下越好，但在低信噪比(-10 dB与-5 dB)条件下基于匹配滑动的多普勒系数估计的性能要好于基于FRFT的多普勒系数估计。

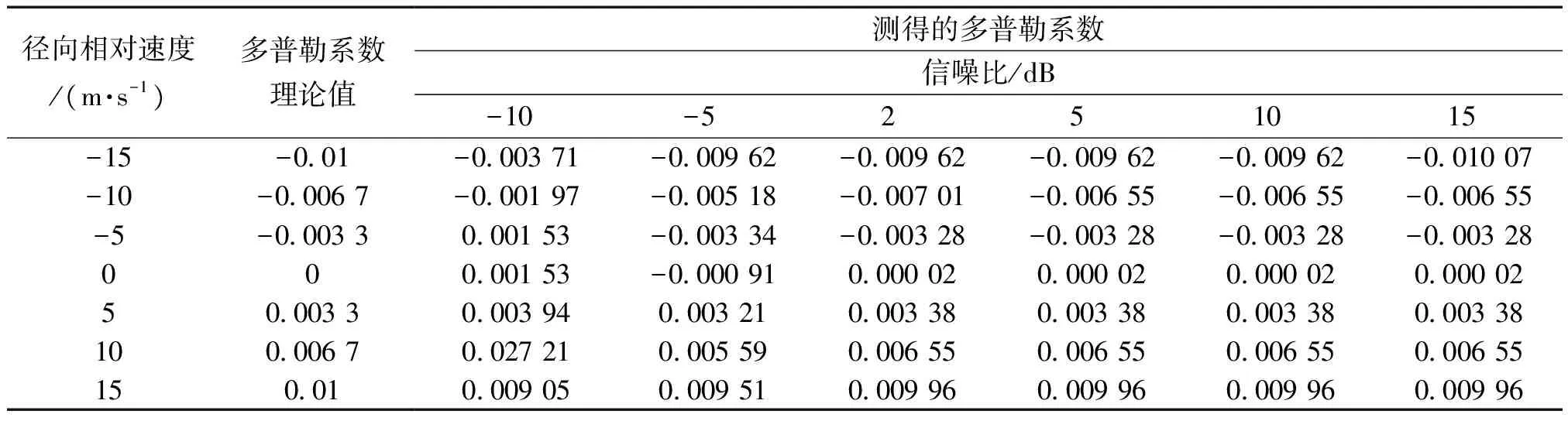
表1 基于FRFT的多普勒系数估计

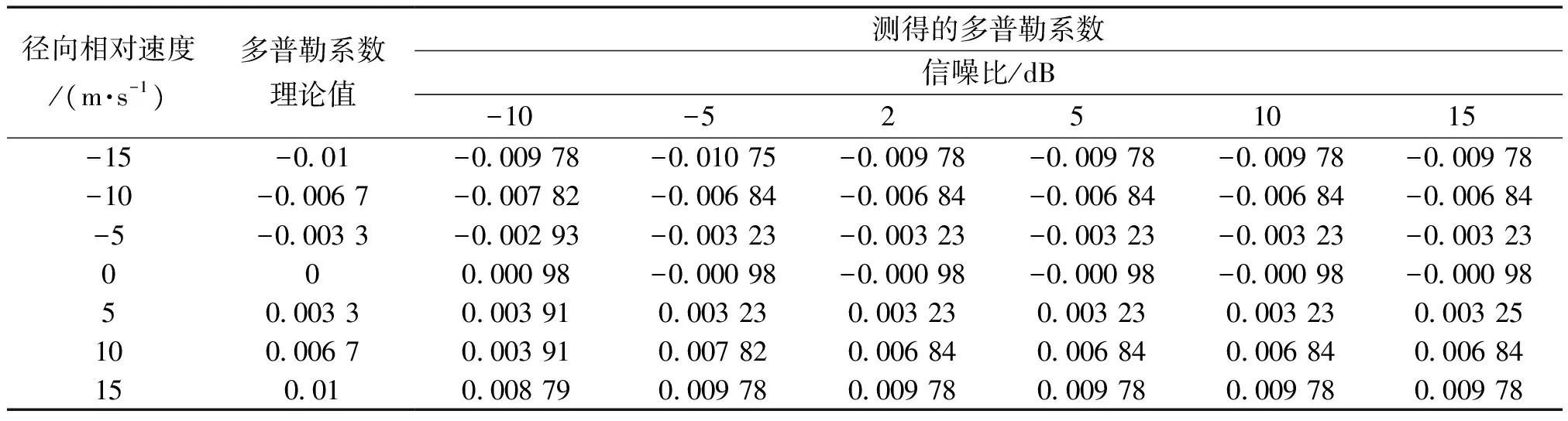
表2 基于滑动匹配的多普勒系数估计

图6给出用2种方法对信号进行多普勒补偿后的误码率曲线并与不补偿的情况下的误码性能作比较，其中径向相对速度为5 m/s。

图6 高斯信道条件下误码率曲线图Fig.6 Bit error rate curve under AWGN channel

由图6可以看出在较低信噪比的情况下(小于-10 dB)基于滑动匹配的多普勒补偿方法的误码性能是要好于基于FRFT的多普勒补偿方法的误码性能，但在较高信噪比条件下(大于-10 dB)情况正好相反，事实与之前的多普勒系数估计的结论是基本一致的。

FRFT多普勒补偿和滑动匹配多普勒补偿这两种方式都是利用一个同步信号估计出整体的多普勒补偿系数，再对整个系统进行统一补偿，也就是多普勒系数是固定的，接下来仿真船速在5～10 m/s随时间变化条件下的性能，并在有多途效应影响和无多途效应影响的两种情况下再对结果进行仿真，仿真信道如图7所示。

图7 仿真信道冲激响应Fig.7 Simulated underwater acoustic channel response

图8为滑动匹配跟踪算法对每个码元进行跟踪估计的估计值并与理论值进行比较，以1 000个码元为例，根据表1、2可知理论估计值应该在0.003 3～0.006 7浮动。由图8可以看出，在无多途效应干扰的情况下，多普勒系数估计的效果较为准确，基本在理论值上下一个采样点浮动，在有多途效应干扰的情况下，部分多普勒系数估计值与理论值存在偏差，但是这种偏差并不会累计和影响到下一次估计值的准确性，对整体一整帧信号影响不大，具有较强的稳定性和可靠性。

图8 滑动匹配跟踪多普勒系数估计值Fig.8 Comparison between estimated and theoretical value

图9给出船速在5～10 m/s浮动时两种情况的误码率曲线。由图9可以看出在船速浮动的情况下，无多途情况的误码性能要优于有多途情况的误码性能2 dB左右。在有多途的情况下，信噪比高于-2 dB时，误码率接近于0，可以推测这种方法在实际应用中也有较高的可靠性。

图9 仿真水声信道条件下误码率曲线Fig.9 Bit error rate curve under simulated underwater acoustic channel

图10为船速在5～10 m/s浮动时3种补偿方法的误码率曲线。由该图可以看出在船速浮动的情况下，之前的FRFT补偿的效果非常差，基于FRFT的多普勒补偿后的误码率曲线基本与无多普勒补偿的误码率曲线一致，而滑动匹配补偿方法则效果明显，在-10 dB以后的补偿效果较好，可靠性很高。

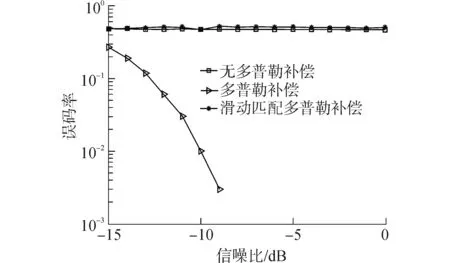
图10 多普勒补偿后误码率曲线Fig.10 Bit error rate curve after Doppler compensation

3.2 海试实验

本文在仿真研究基础上，为验证本方法在真实海洋环境下的性能，在2015年7月在辽宁省大连市长山岛附近海域进行了一次移动水声通信试验。发射船与接收船的相对运动速度约为1.5 m/s，通信距离约为5 km，信道条件如图11所示。

图11 信道估计图Fig.11 Channel estimation figure

由于船速约为1.5 m/s，因此多普勒系数理论值的绝对值应该在0.001左右，图12为用滑动匹配的方法对接收信号进行多普勒系数的估计结果。

由图12可以看出大部分多普勒估计值得绝对值为0.001 041，与理论值基本相等。由于噪声和信道影响，少部分估计值与理论值偏差较大，但本文提出的方法可以估计时变多普勒，并不会影响到下一个码元多普勒系数的估计。最后用滑动匹配的方法对接收信号整体进行了多普勒系数估计补偿并对接收信号进行解调，误码率为0，由于船是匀速运动，所以经过FRFT多普勒补偿后的误码率虽然也为0，而未经多普勒补偿直接解调的误码率为50%左右。

结合仿真研究和海试结果来看，基于滑动匹配的多普勒系数估计方法在可靠性和实用性上都要优于基于FRFT的多普勒系数估计方法。本文所提方法的多普勒系数估计精度可以达到采样率的倒数，而基于FRFT的多普勒系数估计要达到这个估计精度则需要通过缩短分数阶次的步进阶数使其达到一个合适的值，但是这样使得计算量急剧增大，满足不了实际系统中实时运算的要求。而基于滑动匹配的多普勒系数估计则具有计算量小，估计精度高的优点，比基于FRFT的多普勒系数估计方法具有更高的可行性。

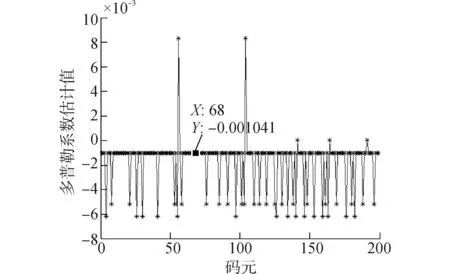
图12 多普勒系数估计图Fig.12 Doppler coefficient estimated figure

4 结束语

1)本文所提出的滑动匹配迭代法在对信号进行多普勒系数是估计的同时实现信息的解调，使其在进行移动水声通信时可以实现对每一个码元的多普勒跟踪。

2)比较了在有多途信道和无多途信道情况下滑动匹配多普勒系数估计方法的性能，两种情况下均可以跟踪时变多普勒，在无多途情况下的性能优于有多途情况下的性能，在变速运动时本文提出的方法效果好。

3)在当前码元多普勒系数估计出现偏差时，通过本文提出的算法在估计下一个码元时可以纠正偏差，克服了误差累积的问题，进而实现正确解码。

4)本文研究方法适用于移动水声通信领域，并且适合在水声通信硬件系统中实现。

[1]程恩, 袁飞, 苏为, 等. 水声通信技术研究进展[J]. 厦门大学学报：自然科学版，2011, 50(2): 271-275. CHENG En, YUAN Fei, SU Wei, et al.Research on technology of underwater acoustic communication[J]. Journal of Xiamen university： natural science, 2011, 50(2): 271-275.

[2]齐林, 陶然, 周思永, 等. 基于分数阶Fourier变换的多分量LFM信号的检测和参数估计[J]. 中国科学辑: E辑, 2003, 33(8): 749-759. QI Lin, TAO Ran, ZHOU Siyong, et al.Signal detection

and parametr estimation based on FrFT[J]. China science(E), 2003, 33(8): 749-759.

[3]EBIHARA T, MIZUTANI K. Underwater acoustic communication with an orthogonal signal division multiplexing scheme in doubly spread channels[J]. IEEE journal of oceanic engineering, 2014, 39(1): 47-58.

[4]朱梦宇, 杨裕亮. 一种适用于水声通信的Doppler 估计算法[J]. 海洋技术, 2006, 24(1): 124-126. ZHU Mengyu, YANG Yuliang. An efficient Doppler estimation algorithm for underwater acoustic communications[J]. Ocean technology, 2006, 24(1): 124-126.

[5]林伟, 陈强, 汪玉.一种有效的水声通信多普勒处理方法[J]. 声学技术, 2005, 24(4): 206-209. LIN Wei, CHEN Qiang, WANG Yu. An efficient Doppler processor for underwater acoustic communications[J]. Technical acoustics, 2005, 24(4): 206-209.

[6]SHARIF B, NEASHAM J, HINTON O, et al. A computationally efficient Doppler compensation system for underwater acoustic communications[J]. IEEE journal of oceanic engineering, 2000, 25(1): 52-61.

[7]ZHANG Xiao, HAN Xiao, YIN Jingwei, et al. Study on Doppler effects estimate in underwater acoustic communication[J]. The journal of the acoustical society of america, 2013, 133(5): 3463-3463.

[8]AVAL Y, STOJANOVIC M. Partial FFT demodulation for coherent detection of OFDM signals over underwater acoustic channels[C]∥Proceedings of MTS/IEEE Oceans Conference. Bergen Norway, 2013: 1-4.

[9]王巍, 尹艳玲, 刘凇佐, 等. 基于频域变采样的OFDM 水声移动通信多普勒补偿算法[J]. 声学技术, 2013, 32(1): 54-58. WANG Wei, YIN Yanling, LIU Songzuo, et al.Doppler compensation of using frequency domain re-sampling in underwater acoustic mobile OFDM communication[J]. Technical acoustics, 2013, 32(1): 54-58.

[10]袁兆凯, 隋天宇, 李宇, 等. 水声扩频通信中多普勒估计与补偿算法研究[J]. 电子与信息学报, 2012, 34(1): 51-56. YUAN Zhaokai, SUI Tianyu, LI Yu, et al.The estimation and compensation of Doppler effect on underwater acoustic spread spectrum communication [J]. Journal of electronics & information technology, 2012, 34(1): 51-56.

[11]WINKLER M. Chirp signals for communications[J], Wes con convention record, 1962, 14(2): 7.

[12]李绍滨, 刘银中. 机载SAR原始回波数据多普勒参数估计的比较[J]. 哈尔滨工业大学学报, 2006, 38(11): 1910-1914. LI Shaobin, LIU Yinzhong. Comparison of different kinds of Doppler parameter estimation from raw data of airborne SAR[J]. Journal of Harbin Institute of Technology, 2006, 38(11): 1910-1914.

本文引用格式：

李增祥，刘磊，赵云江，等. 二元正交Chirp载波水声通信时变多普勒系数估计[J]. 哈尔滨工程大学学报， 2017， 38(7): 1107-1113.

LI Zengxiang, LIU Lei, ZHAO Yunjiang, et al. Doppler coefficient estimation for chirp spread spectrum of binary orthogonal keying system[J]. Journal of Harbin Engineering University， 2017， 38(7): 1107-1113.

Doppler coefficient estimation for chirp spread spectrum of binary orthogonal keying system

LI Zengxiang1, LIU Lei2, ZHAO Yunjiang2, LIU Songzuo2

(1.School of Computer Science & Technology, Shandong University of Technology, Zibo 255000, China; 2.College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China)

For the inconsistency between wideband Doppler and code-element Doppler caused when underwater vehicles under relative motion carry out acoustic communication, this paper proposes a Doppler estimation and demodulation algorithm for the mobile and robust underwater acoustic communication system based on binary chirp signal. After the initial Doppler was attained by processing synchronous signal based on the fraction order of Fourier transform, the relevance between the neighboring code elements was utilized to process neighboring code elements by sliding match and iteration. Thus, the Doppler coefficient estimate for each chirp carrier was realized. To estimate the Doppler coefficient, the intermediate variable was utilized to demodulate signals. Simulation and sea trial results confirm the validity of the proposed approach. A communication effect with bit error rate less than 10-4was achieved via a sea experiment with distance of 5 km and relative velocity of 1.5 m/s.

LFM signal; mobile underwater acoustic communication; fractional Fourier transform; Doppler coefficient estimation; sliding interative matching; signal processing; time vary signal

2016-07-29.

日期：2017-05-26.

国家自然科学基金项目(61401114，61431004)；黑龙江省自然科学基金项目(F2016010)；上海交通大学海洋工程国家重点实验室基金项目(1414).

李增祥(1978-), 男, 讲师, 硕士； 刘凇佐(1986-), 男, 讲师, 博士.

刘凇佐，E-mail: liusongzuo@hotmail.com.

10.11990/jheu.201607080

TN911.5; TB567

A

1006-7043(2017)07-1107-07

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20170526.1838.004.html