斜流中螺旋桨非定常水动力性能的数值分析
2017-08-31常欣梁宁王超孙帅
常欣,梁宁,王超,孙帅
(哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001)
斜流中螺旋桨非定常水动力性能的数值分析
常欣,梁宁,王超,孙帅
(哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001)
斜流是一种相对简单的非均匀来流,其加剧了船艉伴流场的非均匀性,对螺旋桨非定常力非常不利。为了探讨斜流中螺旋桨水动力性能与受力变化的一般规律,本文对DTMB4679螺旋桨斜流中的非定常水动力性能进行计算。计算结果表明:在斜流工况下,桨叶表面压力分布不均匀,是激振力产生的根本原因,并且桨叶表面压力分布不均匀性随进速系数的减小而增大;单片桨叶的受力的脉动幅度随斜流角度的增大而增大;在不同的斜流角度、进速系数下螺旋桨涡结构云图也表现出一定的变化规律。
螺旋桨; 非定常水动力性能; 斜流; 压力分布; 数值模拟; 敞水; 激振力
船艉螺旋桨由于受到船舶操纵状态、不规则水流、总布置要求及航行纵倾等影响,不可避免地处于斜流中工作[1]。斜流对螺旋桨的性能有很大影响,会导致推力和转矩曲线相对敞水状态下发生一定平移,导致螺旋桨效率下降。因此,斜流中螺旋桨非定常性能一直是人们关注的重点之一。孟庆津等将阿·姆·巴辛所著的《螺旋桨原理与计算》中关于斜流中螺旋桨水动力性能计算内容独立翻译成篇,并添加了计算实例[1]。邱振良分析了螺旋桨斜流效应横向力产生原因,及其对船舶操纵性能的影响,针对不同工况给出了具体操纵建议,以便正确操纵船舶[2]。张志荣、洪方文等针对DTMB4679在斜流中的性能进行了试验以及数值方法的研究,结果表明非定常方法计算精度相对较高[3]。Chang P等研究了船舶急停操纵过程中螺旋桨性能变化,在具有横向分量来流的工作环境下,螺旋桨会产生相应的侧向力并使得船舶有一定的艏摇漂移运动,同时还会产生斜流分量,增大螺旋桨的非定常载荷[4]。Mauro S等对双桨军舰的定常回转性能进行了研究,结果表明回转过程中船尾伴流呈非对称分布,船体内侧具有横向速度导致有大量的流体分离现象出现,形成大的涡结构,这表明内外桨处于不同的斜流环境[5]。Giulio Dubbioso等采用重叠网格技术,以E779A为研究对象,对两个不同进速下和多个斜流角度下的螺旋桨性能进行了数值分析,结果表明计算敞水性能和试验值吻合良好,但斜流状态下缺乏试验数据,无法进一步的验证[6]。张文照等以FLUENT为平台,对斜流条件下全附体潜艇模型艇后螺旋桨水动力进行计算,计算结果表明,艇后螺旋桨推力和转矩随着攻角的增大呈现出先减小后增大的趋势,为潜艇操纵性研究中螺旋桨水动力预报问题提供了方法[7]。
本文以DTMB4679螺旋桨为研究对象,开展斜向来流下螺旋桨非定常水动力性能计算,重点分析桨叶表面压力和单片桨叶在旋转过程中的受力变化,并与试验值进行对比。
1 水动力性能计算前处理
1.1 模型与计算域的建立
本次计算模型为DTMB4679螺旋桨,其主要几何参数[9]为:直径D为607 mm,毂径比为0.3,盘面比为0.9,侧斜角度为50°,几何模型如图1所示。美国泰勒水池曾对该桨进行了各种工作条件下的试验研究,包括斜流下螺旋桨性能试验,为本次数值计算方法验证对比提供了试验数据。

图1 几何模型Fig.1 Geometric model
本次计算工况如表1所示,由于敞水条件下螺旋桨性能与斜流来向无关,只与角度大小有关,所以只计算正斜流角度即可,以来流速度U作为螺旋桨进速,计算其进速系数。

表1 DTMB 4679桨的计算工况
本文采取模拟斜流改变来流速度分量,这样对于计算任意斜流角都只需建立一个计算模型,省去了很多工作量。
为了模拟螺旋桨的工作环境[10],建立一个模拟计算域,所建立的计算域包括两部分:一部分需要随螺旋桨同步旋转来模拟螺旋桨的旋转,即旋转域;另一部分要求足够大,即外域。两域均采用与螺旋桨同轴的圆柱流域。如图2所示,前面和左右侧面均定义为速度入口,以便更好地模拟斜向来流,入口来流如图3所示,其中U为来流速度,β为斜流角度,Vx为轴向分量,Vt为切向分量。前入口距桨中心4D,出口距桨中心为6D,前入口截面积为4D×4D,D为螺旋桨直径。
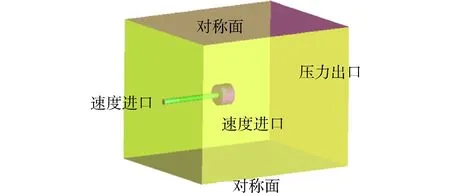
图2 螺旋桨计算域Fig.2 Propeller calculation domain
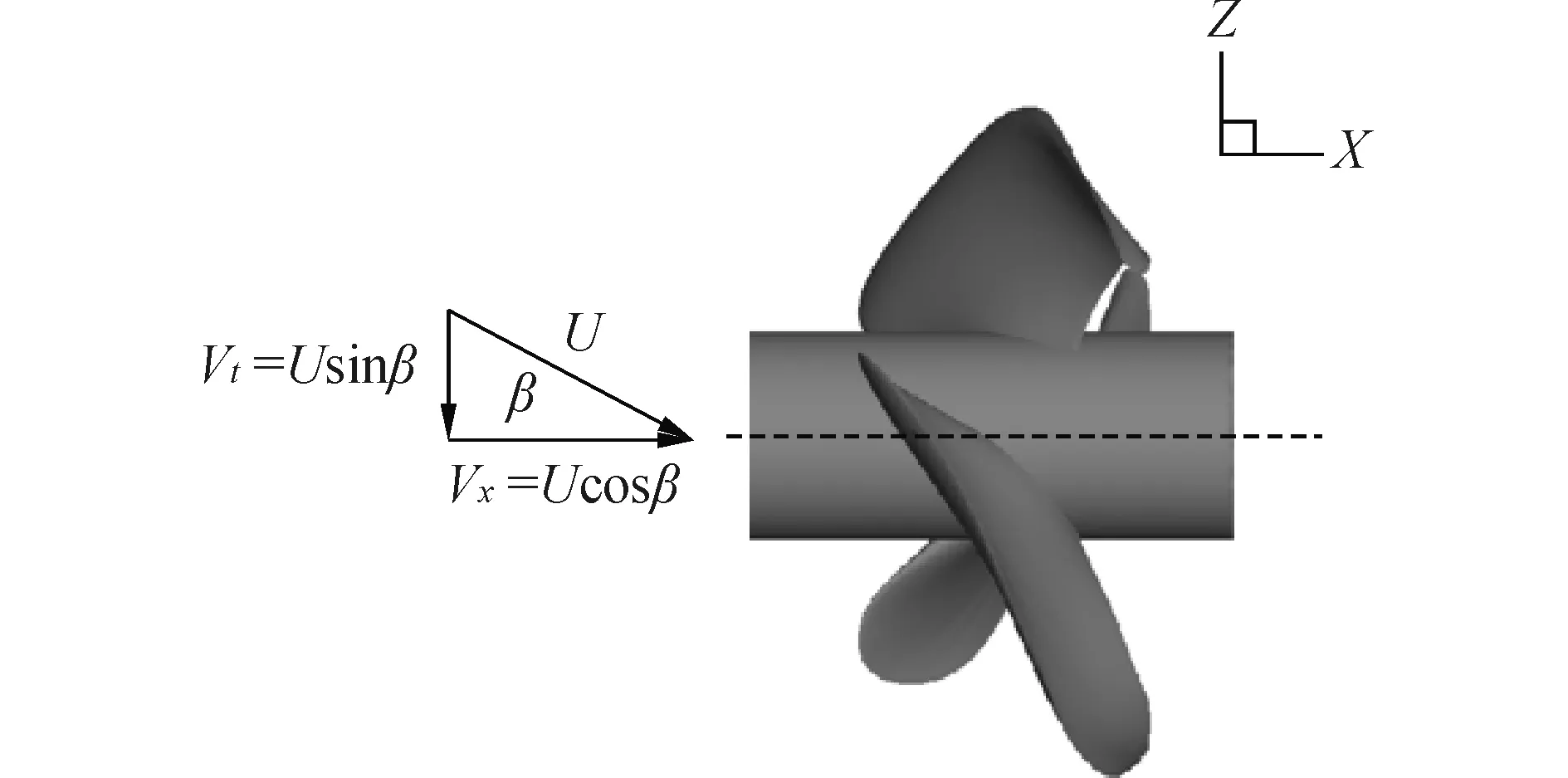
图3 螺旋桨来流示意图Fig.3 Schematic diagram of propeller flow
1.2 计算网格划分
由于DTMB 4679桨为大侧斜桨,划分结构化网格较为困难,网格质量低,因此旋转小域中选择的是四面体非结构化网格[11],对几何适应性更强,如图4(a)所示,生成网格时要注意对导边、随边和叶根等曲率变化大的位置局部加密。另外,为了较好地模拟边界层,桨毂和桨叶表面共生成了8层棱柱网格,如图4(b)所示,首层网格高度为0.000 2 m,对应的Y+约为60,外域几何形状比较规整,采用的六面体结构化网格,同时节省了网格数量,如图4(c)所示。总体计算网格数目为324万左右。
1.3 计算参数设置
采用稳态多参考系(MRF)方法[12],计算定常水动力性能;采用滑移网格方法,计算非定常水动力性能;通过改变来流速度来改变进速系数。
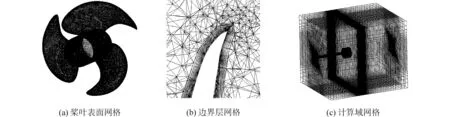
图4 计算网格划分Fig.4 Computational mesh generation
采用SIMPLEC方法进行求解,压力项采用标准方法离散,动量项采用二阶迎风格式离散,收敛因子各项保持默认值;螺旋桨桨叶和桨毂及远场外壁面均定义为不可滑移壁面条件;进口设置为Velocity-inlet,包括前进口和左右侧面进口;外域顶面和底面设置为Symmetry;出口设置为Pressure Outlet,表压设置为0,两域之间利用Interface边界进行连接,流场通过Interface插值进行信息传递。
2 β=0°来流定常计算分析
在计算螺旋桨斜流非定常水动力性能之前,先对斜流角为0,进速系数J=1.078的工况一进行定常计算,以验证计算方法和网格数目的合理性。
在β=0°工况下,螺旋桨推力T为1 960.5 N,转矩Q为298.6 N·m,推力系数KT为0.215 2,转矩系数10KQ为0.539 9。
图5(a)、(b)分别为0.7R和0.9R处叶剖面压力系数分布计算值与试验值对比。
图中显示,整体压力分布计算值与试验值吻合良好,尤其在桨叶中部区域,二者基本一致,表明本文数值方法对大侧斜桨桨叶表面压力分布的模拟基本满足要求。而计算值与试验值之间的差异主要集中在导边和随边附近的测点,图5(a)中可以看到,在叶背导边附近,试验测量时有一个小的压力峰值,但是数值计算并没有很好地模拟出来。图6为桨叶表面压力分布云图,可以更加直观完整地观察到桨叶压表面压力分布。

图5 压力系数分布计算值与试验值对比Fig.5 Comparison between the calculated and experimental values of the pressure confficient distribution

图6 桨叶压力分布云图Fig.6 Blade pressure distribution contour
通过图5、6可以看出在0°来流的工况下,3个桨叶压力分布基本相同,并且在0.7R、0.9R处所得的压力系数可以说明在单个桨叶上压力分布也较为均匀,压力梯度比较小,符合大侧斜桨良好空泡性能的特征。
3 斜流非定常计算分析
3.1 水动力计算结果
调整来流方向与桨轴之间角度为7.5°,对设计进速系数J=1.078(工况2)和另一个稍小的进速J=0.719(工况4)螺旋桨水动力性能进行非定常计算,时间步长约为螺旋桨旋转0.5°所需的时间。
表2 DTMB 4679桨推力和转矩时均值,J=1.078
Table 2 Unsteady thrust and torque of the DTMB4679,J=1.078

参数推力T/N转矩Q/(N·m)推力系数KT转矩系数10KQ定常计算值β=0°1960529860215205399非定常计算时均值β=75°2014330640221105539文献[13]计算值——0211805507文献[14]计算值——02294—β=75°相对β=0°变化值+538+78+271%+256%与文献[13]相对误差/%——429057与文献[14]相对误差/%——368—
分析表2中数据可知,相对β=0°来流,在β=7.5°的斜流中螺旋桨推力和转矩都有一定程度的增幅,分别为2.71%和2.56%,说明斜流中的螺旋桨载荷会加重。另外表中还列出了文献[13]、[14]中的RANS方法计算值,文献[13]是基于StarCCM+软件平台求解的,并采用多面体网格划分桨模,湍流模型为K-ε,文献[14]采用的求解器、网格类型和湍流模型为与本文一致,可以看出本文计算推力结果与文献[14]计算值更为接近,而与文献[13]相比,推力值误差在5%以内,转矩值几乎一致,总的来看,本文计算结果是准确可信的。
表3为工况4的计算结果,从表中数据来看,计算结果与文献值同样吻合良好。
3.2 单片桨叶受力计算分析
为了更加清晰地分析单片桨叶在旋转过程中的受力情况,图7对桨叶1和桨叶2叶剖面进行了水动力分析,并定义正对横向来流的桨叶周向位置为θ=0°,按逆时针方向角度依次增加。叶剖面来流主要包含轴向速度分量和周向速度分量,可以定义为
(4)
(5)
式中:U是斜流速度,ω是螺旋桨旋转角速度,β为斜流角度,θ为桨叶周向位置。在不考虑螺旋桨自身诱导速度的条件下,桨叶旋转一周的过程中轴向来流Vx是恒定不变的,即轴向分速度Vx在螺旋桨盘面上下左右是均匀对称的,它对推力和转矩在各象限的影响是相等。而周向速度则不然,是螺旋桨产生非定常力的主要原因。对于特定的半径位置,桨叶旋转周向速度ωr是一定的,而与周向位置角度θ相关的-Usinβsinθ项在旋转一周过程中是不断变化的,这导致叶剖面的攻角也是随着不断变化的:
(6)
式中:Θ为叶剖面螺距角,从式(6)中可以看出,周向速度分量越大时,叶剖面攻角也越大,桨叶产生的推力也相应越大。图7(b)和(c)中还给出了纯轴向流(β=0°)时的叶剖面攻角,可以看到对于桨叶1位置处,其叶剖面攻角相比纯轴向流时要小的,而桨叶3位置处,其叶剖面攻角相比纯轴向流时要大的。综合分析可以得出如下结论:当θ=90°时,桨叶推力转矩最小;当θ=270°,桨叶转矩最大,这与图7中给出的计算结果一致。
表3 DTMB 4679桨推力和转矩时均值,J=0.719
Table 3 Unsteady thrust and torque of the DTMB4679,J=0.719

参数推力T/N转矩Q/(N·m)推力系数KT转矩系数10KQ非定常β=75°3568147010391608500文献[13]计算值——03760837文献[14]计算值——03822—与文献[13]相对误差/%——406154与文献[14]相对误差/%——2430—
图8为J=1.078时单片桨叶旋转一周过程中推力和转矩变化曲线,图中还列出了挪威技术研究所(MARINTEK)的AKPA代码计算结果和Hoshino的计算结果以供比较。从图中可以看出本文计算的推力系数和AKPA计算值几乎重合,转矩系数在0°~120°也基本一致,而在120°~360°内,本文计算转矩系数相比其他学者的计算值都要略大,但相对误差也是在可接受范围之内的。
调整斜流角度会使得来流轴向和横向分速度发生改变,为了考察斜流角度对其的影响,将进速系数均为J=1.078的工况2(β=7.5°)和工况3(β=15°)的螺旋桨数据加以分析比较。

图7 桨叶剖面水动力分析Fig.7 Hydrodynamic analysis of blade section

图8 单片桨叶推力和转矩系数曲线(β=7.5°,J=1.078)Fig.8 Blade thrust and torque coefficient curve(β=7.5°,J=1.078)
图9为不同斜流角时单片桨叶在旋转一周过程中推力和转矩系数曲线,从图中可以看到斜流角增大后,其推力和转矩波峰和波谷的周向位置并没有发生变化,但是由式(6)可知,横向速度分量增大后会导致叶剖面攻角变化增大,从而使得桨叶推力和转矩的脉动幅度增加,对螺旋桨激振力不利。

图9 不同斜流角时单片桨叶推力和转矩系数变化曲线(J=1.078)Fig.9 Blade thrust and torque coefficient curve with different angle of oblique flow(J=1.078)
3.3 桨叶压力分布计算结果
为了对斜流中的桨叶表面压力分布情况作详细讨论,图10给出了工况2和工况4桨叶表面压力分布云图。
通过图10桨叶表面压力分布云图可以看出:
1)两个不同进速下,桨叶表面压力分布都相对比较均匀,压力变化梯度小,表明大侧斜桨使各半径处的叶切面依次进入高(或低)伴流区,非均匀流场对整个螺旋桨的非定常影响降低,改善了叶表压力分布,提升螺旋桨的空化噪声性能;
2)低进速工况时,不同桨叶之间的桨叶压力分布差异更大,流场的非均匀性体现得更为明显;
3)螺旋桨桨叶压力分布沿横向和垂向存在不同程度的非对称性,致使螺旋桨产生包含6个脉动分量的非定常轴承力,这是螺旋桨产生激振力的根本原因。
为了更好地描述桨叶表面压力分布情况,特将两个进速下r/R分别为0.5和0.7的叶剖面,在周向位置为120°和240°处的压力系数计算值与试验值一起绘制于图11中。
从图11中可以看出,本文对非均匀流场中的桨叶表面压力预报结果与试验值吻合良好,误差主要出现在导边(x/c=0.0)与随边(x/c=1.0)处,可能的原因是:1)由于几何形状的关系,导边和随边附近布置测点相对桨叶中部困难,尤其是叶梢附近,所以试验数据也可能存在一定的误差;2)计算模型为了网格划分方便,简化了导边和随边处的导圆,这和试验模型有差别;3)叶梢、导边和随边附近速度梯度大,压力变化较为剧烈,容易造成数值模拟结果出现较大的误差。

图10 桨叶表面压力分布云图(β=7.5°)Fig.10 Blade pressure distribution contour(β=7.5°)

图11 叶剖面压力系数分布(β=7.5°)Fig.11 Blade section pressure coefficient distribution β=7.5°
叶背和叶面压力在导边附近出现了明显的重叠交叉区域,压力分布图在导边附近均为大开口曲线,且低进速时开口要大于高进速,这说明桨叶剖面的攻角是很小的,甚至为负攻角,从而形成了重叠区域,而压力分布曲线导边处开口越大说明叶剖面攻角相应也较大,对应桨叶载荷越重[15]。
3.4 螺旋桨周围涡结构计算结果
Q判据可以用来识别涡的结构,由Hunt[16]等在1988年提出。图12所示为不同进速系数与不同斜流角时螺旋桨梢涡和毂涡结构。
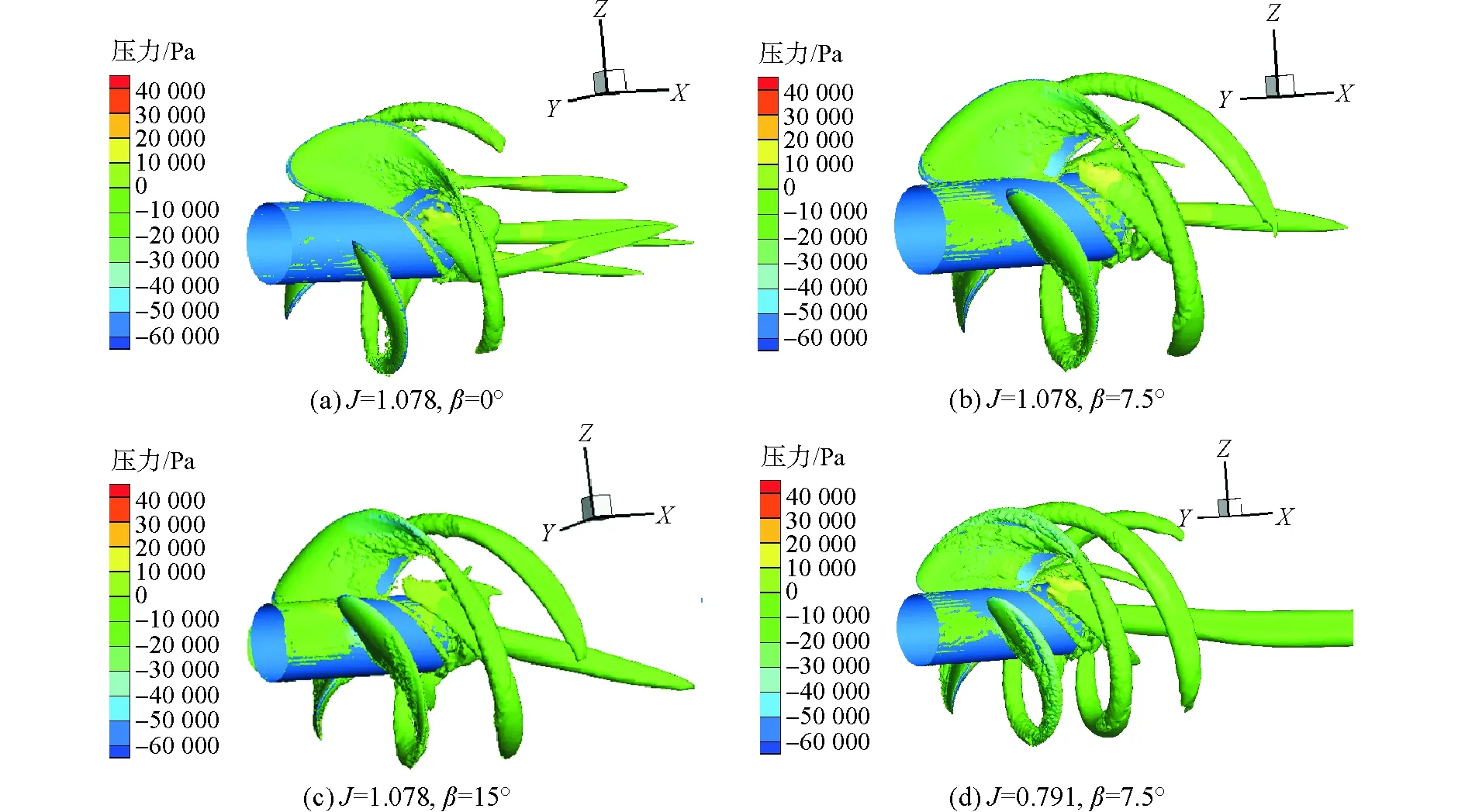
图12 Q=2 000等值面涡结构图Fig.12 Q=2 000 vortex structure ISO surface
对比图12(a)、(b)、(c)可以看出随着斜流角的增加,由于来流具有横向速度分量,毂涡向Z轴负方向偏移;对比(b)、(d)两图可以看出大进速时,梢涡之间的螺距较大,低进速时,螺旋桨梢涡和毂涡强度较大,大量的涡从桨叶表面脱落,从而造成剧烈的湍流脉动。
4 结论
1)相比纯轴向流(β=0°),在斜流中工作的螺旋桨其推力和转矩都会增大,说明斜流中的螺旋桨载荷会加重;
2)斜流中螺旋桨桨叶在旋转一周的过程中,由于周向速度的变化,导致叶剖面攻角也是不断改变的,当θ=90°时,桨叶载荷最小;当θ=270°时,桨叶载荷最大;
3)斜流角增大后,其推力和转矩波峰和波谷的周向位置并没有发生变化,但横向速度分量增大后会导致叶剖面攻角变化增大,从而使得桨叶推力和转矩的脉动幅度增加,对螺旋桨激振力不利;
4)螺旋桨桨叶压力分布沿横向和垂向存在不同程度的非对称性,低进速时更加明显;
5)相同进速系数工况下,毂涡在斜流的影响下有一定的偏移;相同斜流角工况中,毂涡随进速系数减小而增大。
[1]孟庆津. 斜流对螺旋桨工作的影响[J]. 江苏船舶, 1991(3): 18-25. MENG Qingjin.Effect of oblique flow on propeller operation [J]. Jiangsu shipbuilding, 1991(3): 18-25.
[2]邱振良. 螺旋桨斜流效应横向力对船舶操纵影响探析[J]. 中国航海, 1999(2): 36-40. QIU Zhenliang.Effect of horizontal force of propeller slip flow on ship maneuvering [J]. Chinese journal of navigation, 1999(2): 36-40.
[3]张志荣, 洪方文. 斜流中螺旋桨性能数值分析方法研究[C]// 船舶力学学术会议暨船舶力学创刊十周年纪念学术会议, 上海:2007. ZHANG Zhirong, HONG Fangwen.Study on numerical analysis of propeller performance in oblique flow[C]// Academic Meeting of Ship Mechanics Conference and Tenth Anniversary of Ship Mechanics.Shanghai.2007.
[4]CHANG P, ELBERT M, YOUNG Y, et al. Propeller forces and structural response due to crashback[C]∥Proceeding of 27th symposium on naval hydrodynamic. Seoul, Korea, 2008.
[5]MAURO S, DUBBIOSO G, BROGLIA R, et al. Investigation of asymmetrical shaft power increase during ship manoeuvres by means of model tests and CFD[C]∥ Proceeding of 29th Symposium on Naval Hydrodynamics. Gotheborg, 2012.
[6]DUBBIOSO G, MUSCARI R, DI MASCIO A. Analysis of a marine propeller operating in oblique flow[J]. Comput fluid, 2013, 75: 86-102.
[7]张文照, 肖昌润. 斜流中艇后螺旋桨水动力数值计算方法[J]. 舰船科学技术, 2014, 36(2): 55-59. ZHANG Wenzhao, XIAO Changrun.Numerical calculation method of propeller hydrodynamic force in obliquemid-boat [J]. Ship science and technology, 2014, 36 (2): 55-59.
[8]纪兵兵,陈金瓶. ANSYS ICEM CFD 网格划分技术实例详解[M].北京:中国水利水电出版社, 2012: 252-255.
[9]胡健. 螺旋桨空泡性能及低噪声螺旋桨设计研究[D].哈尔滨:哈尔滨工程大学, 2006. HU Jian. Propeller airfoil performance and low noise propeller design research[D].Harbin: Harbin University of Engineering, 2006.
[10]赵峰,吴乘胜,黄少锋,等. 数值水池路线图[J]. 船舶力学, 2014(8): 924-932. ZHAO Feng,WU Chengsheng.Route map on virtual tank[J].Journal of ship mechanics, 2014(8): 924-932.
[11]王超.螺旋桨水动力性能、空泡及噪声性能的数值预报研究[D].哈尔滨: 哈尔滨工程大学,2010. WANG Chao.The research on performance of propeller's hydrodynamics,cavitationg and noise[D]. Harbin :Harbin Engineering University, 2010.
[12]王超, 黄胜, 解学参. 基于CFD方法的螺旋桨水动力性能预报[J]. 海军工程大学学报, 2008, 20(4): 107-112. WANG Chao,HUANG Sheng,XIE Xueshen. Hydrodynamic performance prediction of some propeller based on CFD[J]. Journal of Naval University of Engineering, 2008, 20(4):107-112.
[13]GAGGERO S, VILLA D, BRIZZOLARA S. RANS and PANEL method for unsteady flow propeller analysis[C]∥Proceedings of the 9~(th) International Conference on HyDrodynamics.Shanghai, 2010.
[14]KRASILNIKOV V, ZHANG Z, HONG F. Analysis of unsteady propeller blade forces by RANS[C]∥First International Symposium on Marine Propulsors Smp′09. Trondheim, Norway, 2009.
[15]DUBBIOSO G, MUSCARI R, MASCIO D A. Analysis of a marine propeller operating in oblique flow[J]. Comput fluid, 2013,75:86-102.
[16]HUNT J C R, WRAY A A, MOIN P. Eddies, stream, and convergence zones in turbulent flows[R]. Center for Turbulence Research Report CTR-S88, 1988.
本文引用格式:
常欣,梁宁,王超,等. 斜流中螺旋桨非定常水动力性能的数值分析[J]. 哈尔滨工程大学学报, 2017, 38(7): 1048-1055.
CHANG Xin, LIANG Ning, WANG Chao, et al. Numerical analysis of unsteady hydrodynamic performance of propeller in oblique flow[J]. Journal of Harbin Engineering University, 2017, 38(7): 1048-1055.
Numerical analysis of unsteady hydrodynamic performance of propeller in oblique flow
CHANG Xin, LIANG Ning, WANG Chao, SUN Shuai
(College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)
Oblique flow is a relatively simple non-uniform flow that is unfavorable for the unsteady force of the propeller as it may exacerbate the non-uniformity of the stern wake field. In order to explore the general law between the hydrodynamic performance of the propeller and the force change in the oblique flow, we thus calculated the unsteady hydrodynamic performance of the DTMB4679 propeller in the oblique flow. Calculation results indicate the non-uniform pressure distribution on the surface of the blade under the oblique flow condition, which is the root cause of the exciting force. Furthermore, the unevenness of the pressure distribution on the blade surface increases with the decrease of the speed coefficient, and the fluctuation amplitude of the force of a single blade increases with the increase of the oblique angle. Finally, the cloud chart of the vortex structure of the propeller demonstrates a certain variation law at different oblique angles and speed coefficients.
propeller; unsteady hydrodynamic performance; oblique flow; pressure distribution; numerical simulation; open water; exciting force
2016-05-21.
日期:2017-04-26.
国家自然科学基金项目(51379040,51679052);工信部高技术船舶科研基金项目.
常欣(1978-), 男,副教授; 王超(1982-),男,副教授,博士.
王超,E-mail: wangchao0104@hrbeu.edu.cn.
10.11990/jheu.201605075
U661.3
A
1006-7043(2017)07-1048-08
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20170426.1802.086.html
