爆破振动对地下管道影响试验及风险预测

张黎明， 赵明生， 池恩安,2， 黄 波， 何兴贵

(1.贵州大学 矿业学院， 贵阳 550025； 2. 贵州新联爆破工程集团有限公司， 贵阳 550002； 3.中国矿业大学(北京) 力学与建筑工程学院， 北京 100083)

爆破振动对地下管道影响试验及风险预测

张黎明1， 赵明生2,3， 池恩安1,2， 黄 波1， 何兴贵1

(1.贵州大学 矿业学院， 贵阳 550025； 2. 贵州新联爆破工程集团有限公司， 贵阳 550002； 3.中国矿业大学(北京) 力学与建筑工程学院， 北京 100083)

为了降低爆破振动有害效应，探究爆破振动对地下管道的影响，需基于管道破坏的应变准则，建立爆破振动质点峰值速度与管道破坏的对应关系。利用TC-4850N爆破振动测试仪、DH3820静态应变测试系统在大龙经济开发区高铁城棚户区山地场平工程进行爆破现场试验；对获得不同爆心距、不同最大段装药量时管道地表振动峰值速度及相应管道轴向、环向应变，进行拟合分析，结果表明合成峰值振速与地下管道轴向、环向应变呈指数函数关系；结合该场地条件下爆破振动衰减规律及管道最大容许应变，预测出试验条件下管道所能承受的地表最大峰值振速及此爆破条件下管道爆破施工安全距离。分析表明，燃气管道50 m范围内禁止爆破施工的规定有待改进，应根据实际情况分析预测地下管道安全距离。

爆破振动；峰值振速；应变；拟合分析；安全判据

随着城镇化进行的发展，工程爆破的环境日益复杂，虽然《爆破安全规程》(GB 6722—2014)明确了对地面建筑物、设备及地下构筑物的爆破振动判据，但对爆破振动下地下管道的安全判据尚未建立[1]。在生产实际中经常遇到各类的地下管道，很多学者对此做了大量研究。如文献[2]对在役油气管道周边爆破作业进行了风险分析，提出了定量计算爆破振动等有害效应对管道的影响；文献[3]基于SIMQKE_GR程序模拟爆破地震波，分析其对地下输气管道的影响；文献[4]利用三维薄圆柱模型模拟，结合解析法得出爆破地震波对管道形成的应力分布表达式；文献[5]根据TC-4850爆破振动测试仪现场监测结果对周边存在埋地输油管道的爆破施工方案进行优化；文献[6]提出了爆炸地冲击作用对埋地管线应力计算的解析解算法；文献[7]基于现场试验检测爆炸作用下，埋地管道应力应变，得到岩石中管道的动力响应；文献[8]分析了自然地震的地震波对地下管道的影响；文献[9]根据地下管道地震响应的振动台试验进行数值模拟分析；文献[10-11]利用计算机软件分析有效降低爆破振动的合理延时间隔。大多研究主要借助数学方法和计算机模拟分析爆破振动对管道影响，而较少运用现场直接监测的方法进行研究，数学方法和计算机模拟是在较为理想条件下进行的，现场试验可以更直接反映出爆破振动对管道的影响且更贴近工程实际。因此，本研究利用TC-4850N爆破振动测试仪和DH3820静态应变测试系统分别对爆破振动、地下管道应变进行现场监测，分析爆破振动对地下管道应变的影响规律。并结合管道最大容许应变预测管道的地表最大峰值振速。

1 试验方法

大龙经济开发区高铁城棚户区山地场平工程爆破施工区域地质构造较简单，节理、岩溶较发育，未发现断层。岩石普氏系数f=8.0～10。钻孔直径d=90 mm；梯段高度H=6 m；底板抵抗线Wmax为3 m；实际钻孔长度L=6.5 m；填塞长度h0=2.1 m；孔间距a=3 m；孔排距b为2.5～3 m；单耗约为0.40 kg/m3。爆破器材：非电毫秒导爆管雷管(5段、7段、15段毫秒导爆管雷管)；直径70 mm2#岩石乳化炸药。

1.1 试验目的

试验旨在探究爆破振动对地下管道的影响规律。即最大段装药量、测点距离、爆破振动振速、地下管道应变四者之间的关系。试验确定因素(条件)：爆破区域地质环境条件、管道类型、管道埋深及敷设方式、最大容许应变等。变化因素(条件)：最大段装药量、管道与爆区中心的距离等。

1.2 试验仪器

(1)爆破振动测试仪(TC-4850N)，爆破振动监测采用TC-4850N爆破测振仪。如图1所示。

(2)静态应变测试系统(DH3820)，DH3820是高速静态应变数据采集仪(见图2)，能捕捉材料应力应变整个过程的缓变信号。

1.1 试验步骤

(1)试验准备。选用DN100热镀锌钢管4根，3 m/根，钢管母材为Q235钢。选材原因：①根据相关文献资料，小口径地下管道较大口径管道更易受震害影响[12-13]；②DN100钢管使用范围广，材料主流；③管道长达3 m，应变片贴于钢管中部，可近似忽略管道两端影响。

图1 TC-4850N测试仪 图2 DH3820应变测试系统Fig.1 TC-4850N vibration meter Fig.2 DH3820 strain test system

(2)应变片安装。应变片先与端子焊接，再采用120R三线制1/4桥的桥路连接方式与屏蔽线焊，最后贴于管道中部表明。每根管道贴两个应变片，分别与管道轴向、环向平行，如表1所示。

(3)测点布置。根据爆破区域地形环境、施工情况选择管道埋设位置。在爆破区域的一侧选择符合敷设条件、可安放测振仪、应变仪的测点，布置如图3所示，相关信息列于表1。

(4)管道埋设。管道填埋方式为直埋式，利用大型挖掘机械开挖管沟并填埋。填埋过程中注意保护应变片完好，并标记好每根屏蔽线对应的管道轴向或环向。

(5)应变仪安装。DH3820控制器与电源、电脑、数据采集器连接，然后进行调试。打开8个检测通道分别对应1号、2号、3号、4号管轴向、径向应变。

(6)测振仪安装。用石膏粉将三向速度传感器固定于地下管道中部的地表，x方向对准爆区中心。

(7)数据采集。准备就绪后，TC-4850N保持开机状态等待触发。起爆前点击DH3820软件开始采集应变数据。起爆后，TC-4850N记录下爆破振动信号，DH3820收集管道应变信号。

表1 测点布置相关信息

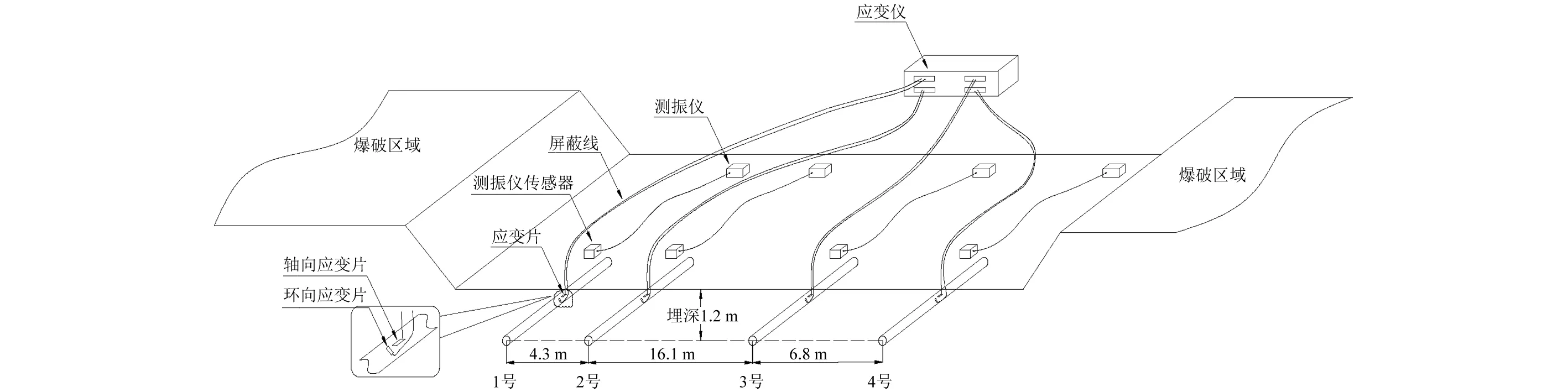
图3 试验测点及仪器布置图Fig.3 Measuring point and instrument distribution

2 试验数据

试验进行6次，测得6组振动数据和应变数据，每组4台测振数据及7个应变数据(3号管道轴向应变片受损，未检测到有效应变数据)，一共24个三向振动信号和42个应变数据，管道应变是管道受振动影响而发生的微小形变，相较于应力可直接描述管道形状的变化程度，因此试验用管道应变而非应力表示管道受振动影响程度。

2.1 测振数据

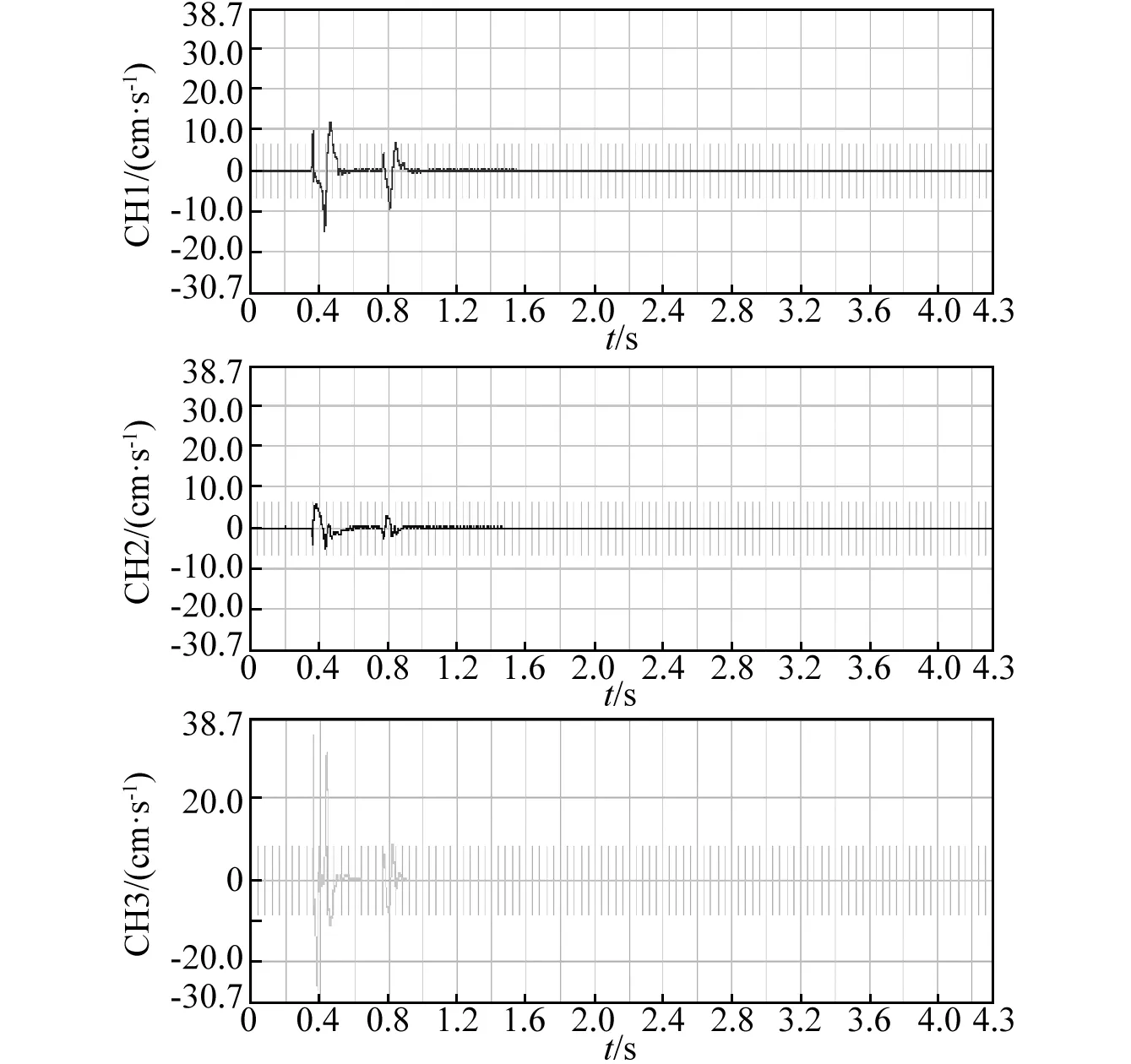
图4 试验1 1号测振仪振动波形图Fig.1 Vibration waveform of No.1 vibration meter of test 1

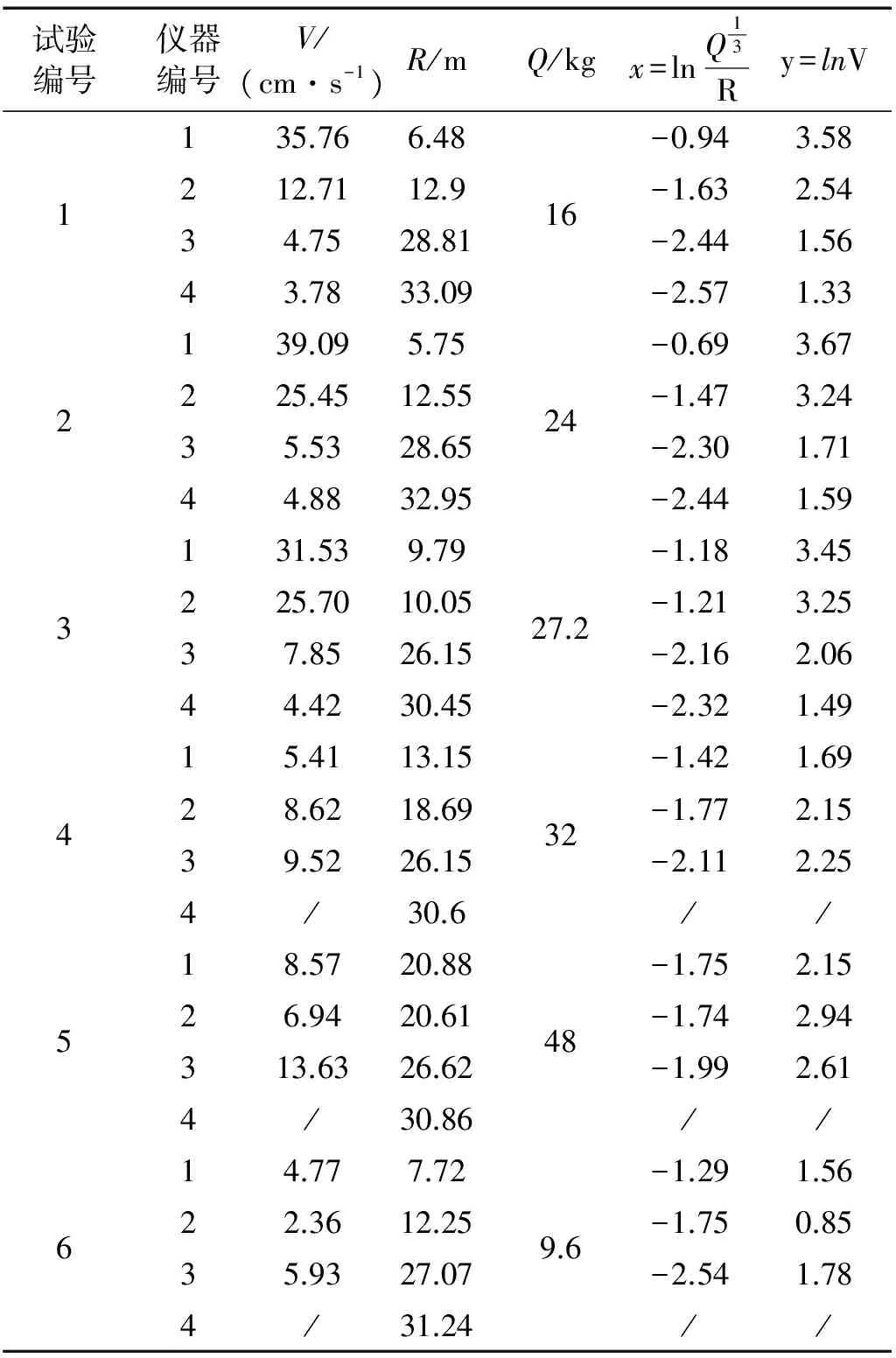
试验编号仪器编号V/(cm·s-1)R/mQ/kgx=lnQ13Ry=lnV123456135．766．48212．7112．934．7528．8143．7833．09139．095．75225．4512．5535．5328．6544．8832．95131．539．79225．7010．0537．8526．1544．4230．4515．4113．1528．6218．6939．5226．154/30．618．5720．8826．9420．61313．6326．624/30．8614．777．7222．3612．2535．9327．074/31．24162427．232489．6-0．943．58-1．632．54-2．441．56-2．571．33-0．693．67-1．473．24-2．301．71-2．441．59-1．183．45-1．213．25-2．162．06-2．321．49-1．421．69-1．772．15-2．112．25//-1．752．15-1．742．94-1．992．61//-1．291．56-1．750．85-2．541．78//

2.2 应变数据

DH3820记录相应通道微应变με即应变ε的106倍。曲线中正值表示拉应变，负值表示压应变，应变实时曲线因电磁干扰，出现均匀的上下波动属于正常现象，因此对均匀干扰部分进行处理。试验1通道2(1号环向)应变曲线如图5所示。统计轴向、环向应变最大值、最小值列于表3。试验中3号管轴向应变通道无法检测平衡，未检测到有效数据。

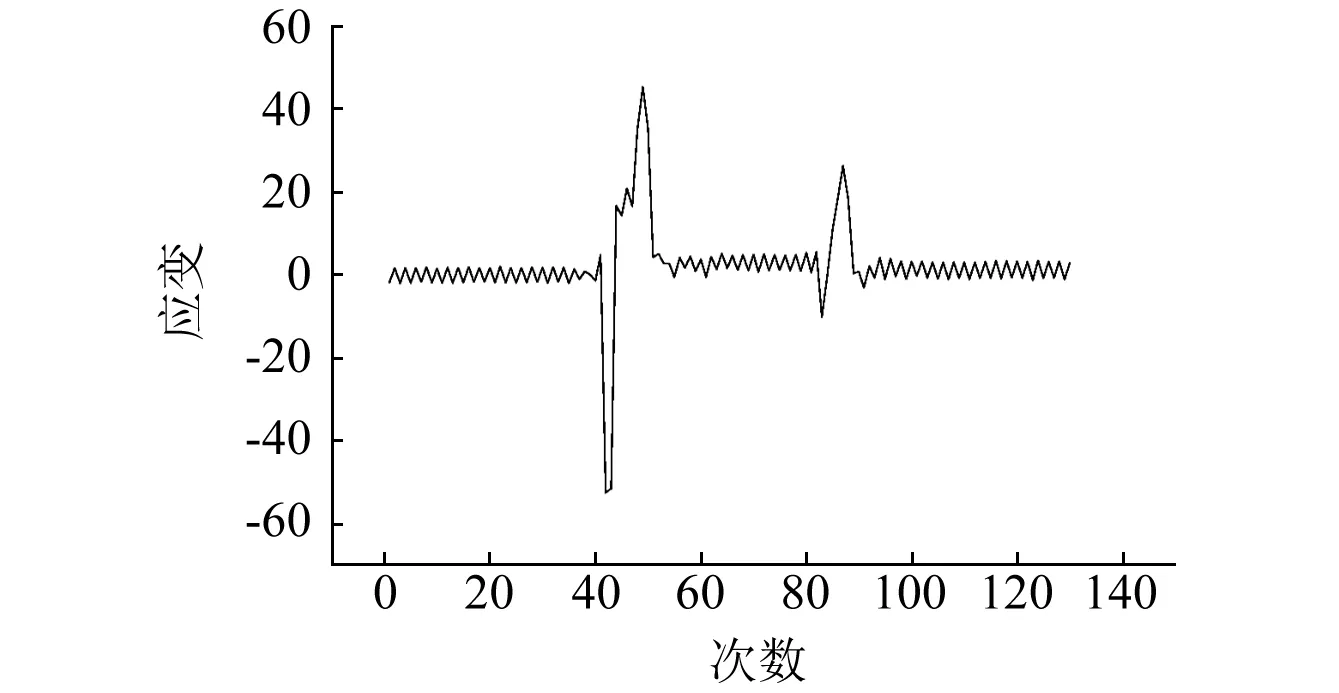
图5 试验1通道2(1号环向)应变曲线Fig.5 Strain curve of No.1 circumferential strain of Test 1

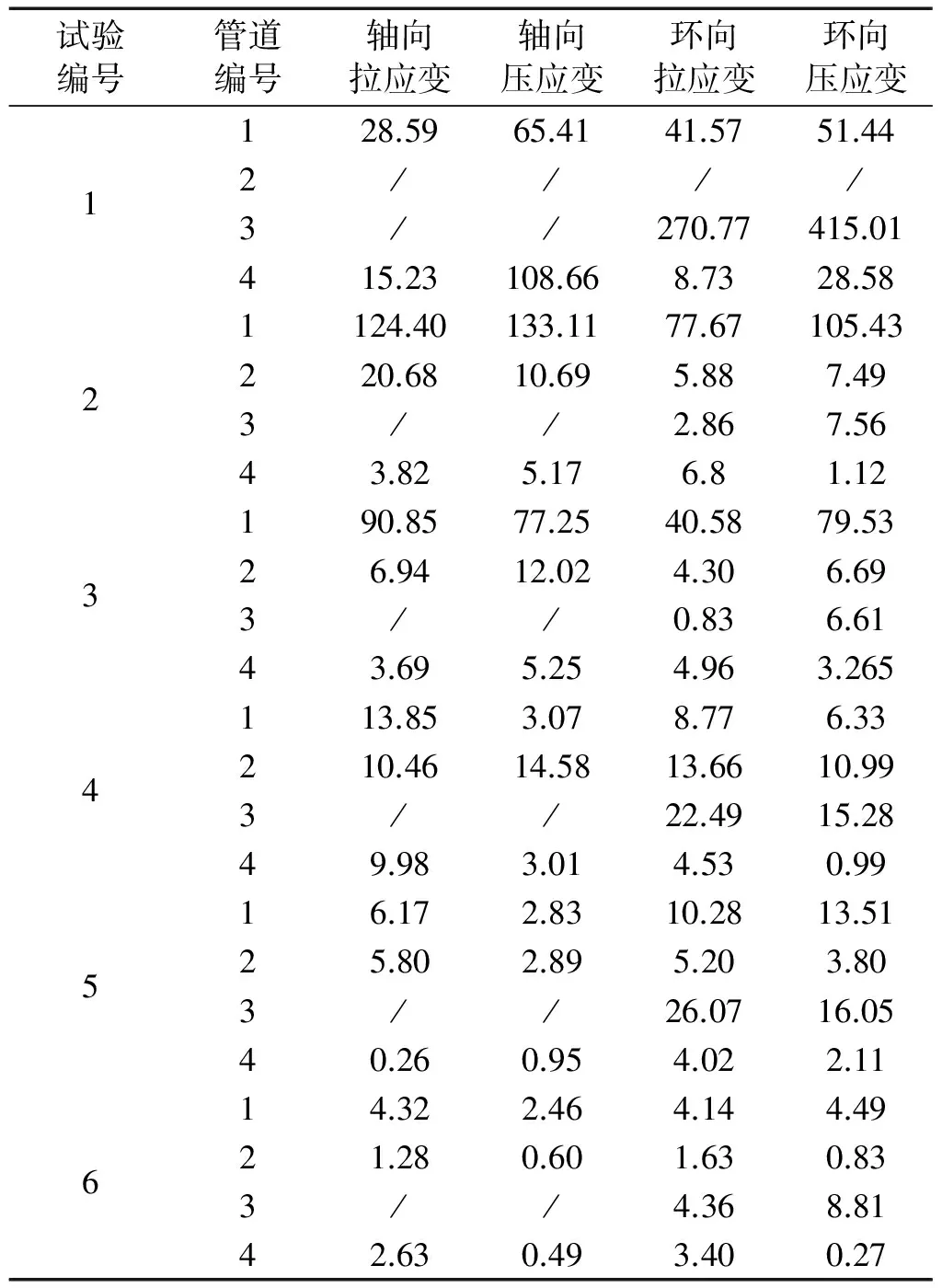
试验编号管道编号轴向拉应变轴向压应变环向拉应变环向压应变123456128．5965．4141．5751．442////3//270．77415．01415．23108．668．7328．581124．40133．1177．67105．43220．6810．695．887．493//2．867．5643．825．176．81．12190．8577．2540．5879．5326．9412．024．306．693//0．836．6143．695．254．963．265113．853．078．776．33210．4614．5813．6610．993//22．4915．2849．983．014．530．9916．172．8310．2813．5125．802．895．203．803//26．0716．0540．260．954．022．1114．322．464．144．4921．280．601．630．833//4．368．8142．630．493．400．27

3 数据分析

3.1 基于萨道夫斯基公式的振动数据线性回归分析

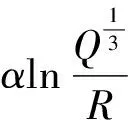
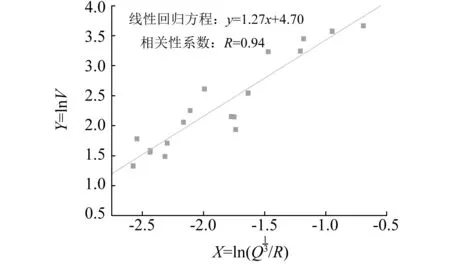
图6 峰值振速线性回归分析Fig.6 Linear regression of peak velocity

3.2 合成峰值振速与各应变的拟合分析

以峰值振速为自变量，应变为因变量，对峰值振速与应变进行拟合分析，去掉一个偏差较大点分析发现二者呈现指数增长关系。峰值振速与轴向拉应变、轴向压应变关系如图7、图8所示；与环向拉应变、环向压应变关系如图9、图10所示。

如图7～图10所示：①管道最大轴向拉应变为1.24×10-4、最大轴向压应变为1.33×10-4，最大环向拉应变为7.77×10-5、最大环向压应变为1.04×10-4，根据4.1节计算结果可知，轴向环向应变均未超过管道最大容许应变，管道试验过程中应变均在弹性范围内；②相同振速条件下轴向应变大于环向应变；③管道受破坏程度与爆破振动振速成正相关，随着峰值振速的增大，管道应变成指数增长趋势；④当振速较小时，管道形变较小；当振速超过一定范围时，管道应变随之突然增大，由此可见爆破振动安全振速范围的重要性。

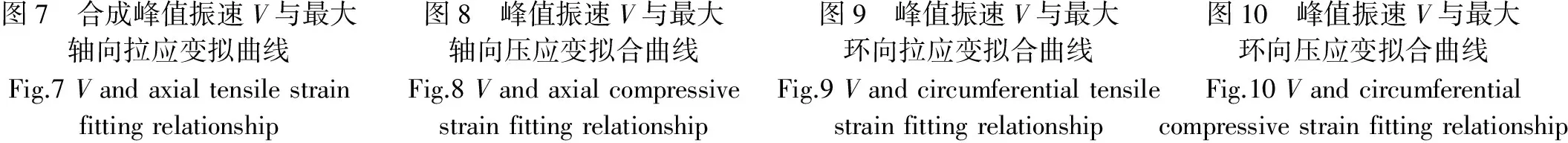
图7 合成峰值振速V与最大轴向拉应变拟曲线图8 峰值振速V与最大轴向压应变拟合曲线图9 峰值振速V与最大环向拉应变拟合曲线图10 峰值振速V与最大环向压应变拟合曲线Fig．7VandaxialtensilestrainfittingrelationshipFig．8VandaxialcompressivestrainfittingrelationshipFig．9VandcircumferentialtensilestrainfittingrelationshipFig．10Vandcircumferentialcompressivestrainfittingrelationship

4 地下管道受震害影响风险预测

4.1 计算管道最大容许应变

(1)试验采用DN100的热镀锌Q235钢管，外径D=114.3 mm；壁厚δn=4 mm；泊松比μ=0.3；回填温度t1=25℃；管道弹性屈服强度和塑性屈服强度分别为：σ1= 282 MPa、σ2=425 MPa；弹性模量E=2.0×105Mpa；弹性区应变ε=0.001 4；伸长率20%。管道、管材参数如表5所示。

(2)计算管道应变[14]

根据《输油(气)钢质管道抗震设计规范》，取相当于设计疲劳曲线应变循环总数为40～50次的应变值为埋地管道的容许拉伸应变[εt] =1%[16]。假定埋地管道的直管段在地震波中所产生的应变是全截面均匀的拉伸或压缩。

管道容许压缩应变

管道正常工作条件下的应力应变

轴向应力为

σL=μσh+E1α(t1-t2)=69.778MPa

式中：管材线膨胀系数α=12.68×10-6℃-1;工作温度t2=50 ℃。

环向应力为

式中：d为管道内径;工作压力P=1.6 Mpa。

轴向应变为

环向应变为

(3)轴向应变组合

假定爆破地震波没有破坏与管道接触介质的完整性和连续性，振动引起的最大轴向应变与管道工作状态下引起的应变组合计算如下所示。

若管道产生拉伸应变：εmax+εL≥0，εmax+εL≤[εt]v，其中[εt]v=1%，εL=3.49×10-4，故εmax≤ 9.65×10-3。

综上所述，-1.25×10-2≤εmax≤ 9.65×10-3为管道轴向容许承受应变范围。

(4)环向应变组合

若管道产生拉伸应变：εmax+εh≥0，εmax+εh≤[εt]v，其中[εt]v=1%，εh=1.06×10-4，故εmax≤9.89×10-3。

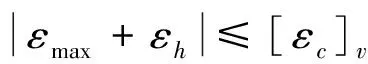
综上所述，-1.23×10-2≤εmax≤9.89×10-3为管道环向容许承受应变范围。

因此，管道轴向和环向容许应变值如表4所示。

表4 管道轴向和环向最大容许应变

4.2 风险预测

地下管道应变y随峰值振速V的变化趋势呈指数函数关系，二者拟合曲线列于表5。

表5 峰值振速与应变拟合曲线

据此进行爆破振动对地下管道的风险预测。用峰值振速表示应变，且应在轴向拉应变、轴向压应变、环向拉应变、环向压应变的最大容许范围内

表6 不同最大段装药量Qmax下的安全距离R

地下管道与爆破区域距离较近时，须严格控制最大段装药量，根据该工程爆破施工实际情况，最大段装药量控制在300 kg以下，因此管道的安全距离为25.25 m，而《石油天然气管道保护条例》规定“管道中心线两侧或者管道设施场区外各50 m范围内禁止爆破”。因此，爆破施工区域附近存在地下管道，应根据爆区地质地形条件、爆区周围环境、地下管道分布等实际情况控制爆破振动效应，可根据现场爆破振动、管道应变监测，分析监测结果为合理优化爆破施工设计方案提供可靠依据。

5 结 论

(1)通过试验研究发现，地表合成峰值振速与地下管道轴向、环向应变呈指数函数关系。

(2)地下管道附近进行爆破施工时，应根据现场实际条件预测管道地表最大峰值振速及爆破施工安全距离从而指导爆破施工。因而，仅仅规定“50 m范围禁止爆破施工”是不科学的。

本文提供了一种切实可行的试验监测方法：基于管道相关资料和管道破坏应变准则，建立峰值速度与管道破坏的对应关系，根据地表振动信号预测地下管道最大允许峰值振速，进而预测地下管道的爆破施工安全距离。实际生产中，地质条件、管道填埋方式、埋深、失效形式不同的情况下，爆破振动对管道的影响有待进一步深入研究。

[ 1 ] 爆破安全规程：GB 6722—2014 [S].北京： 中华人民共和国国家质量监督检验检疫总局, 2014.

[ 2 ] 戴联双, 张海珊, 孟国忠， 等. 在役油气管道周边爆破作业风险分析[J]. 油气储运, 2012, 31(11): 801-803.

DAI Lianshuang, ZHANG Haishan, MENG Guozhong, et al. Oil & gas storage and transportation[J]. Oil & Gas Storage and Transportation, 2012, 31(11): 801-803.

[ 3 ] 彭星煜, 梁光川, 张鹏, 等. 人工爆破地震作用下输气管道动力响应分析[J]. 天然气工业, 2012, 32(11): 81-84.

PENG Xingyu, LIANG Guangchuan, ZHANG Peng, et al. Dynamic response for buried gas pipelines under artificial explosion[J]. Natural Gas Industry, 2012, 32(11): 81-84.

[ 4 ] KOURETZIS G P, BOUCKOVALAS G D, GANTES C J. Analytical calculation of blast-induced strains to buried pipelines[J]. International Journal of Impact Engineering, 2007, 34(10): 1683-1704.

[ 5 ] 范芝宇, 邵鹏, 周利芬, 等. 直立边坡控制爆破对地下输油管道的影响与方案优化[J]. 工程爆破, 2012, 18(2): 42-45.

FAN Zhiyu, SHAO Peng, ZHOU Lifeng, et al. Influence of controlled blasting of vertical slope on buried pipeline and its blasting scheme optimization[J]. Engineering Blasting , 2007, 18(2): 42-45.

[ 6 ] 都的箭, 梁学莹, 邓正栋, 等. 埋地管线爆炸地冲击作用下解析解计算研究[J]. 爆破, 2011, 28(3): 21-25.

DU Dejian, LIANG Xueying, DENG Zhengdong, et al. Research on analytic calculation method of buried pipelines under explosion ground shock waves[J]. Blasting, 2011, 28(3): 21-25.

[ 7 ] ESPARZA E D. Pipeline response to blasting in rock: L51661e[R]. Pipeline Research Council International Catalog, 1991.

[ 8 ] 吴奎. 城市供水管网系统的抗震可靠性分析[D].武汉: 华中科技大学, 2011.

[ 9 ] 金炜枫. 饱和砂土中地下管道地震响应的固体双尺度-流体耦合模拟[J]. 土木工程学报, 2014(增刊1): 221-226.

JIN Weifeng. Coupled fluid/two-scale-solids simulation of buried pipe in saturated sand under seismic excitation[J]. China Civil Engineering Journal, 2014(Sup1): 221-226.

[10] 赵明生, 梁开水, 余德运, 等. 段数对爆破振动信号的时频特性影响分析[J]. 煤炭学报, 2012, 37(1):55-61.

ZHAO Mingsheng, LIANG Kaishui, YU Deyun, et al. Effect of segments on time frequency characteristics of blasting vibration signals[J]. Journal of China Coal Society, 2012, 37(1): 55-61.

[11] 李顺波, 杨军. 孔间不同毫秒延时对爆破振动影响的数值模拟[J]. 煤炭学报, 2013(增刊2): 325-330.

LI Shunbo, YANG Jun. Numerical simulation the effected of blasting vibration for different millisecond delay between the blast-hole [J]. Journal of China Coal Society, 2013(Sup2): 325-330.

[12] 郭恩栋, 余世舟, 吴伟. 地下管道工程震害分析[J]. 地震工程与工程振动, 2006, 26(3): 181-183.

GUO Endong, YU Shizhou, WU Wei. Seismic damage analysis of buried pipeline engineering[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(3): 181-183.

[13] 解晓杰. 埋地供水管道受地震破坏规律的研究[D].成都: 西南交通大学, 2012.

[14] 佘艳华. 机械冲击载荷对邻近埋地管道的影响及控制研究[D]. 北京: 中国工程物理研究院, 2012.

[15] 邓民宪, 高晓康, 张永凯. 地下管道震害预测实用方法的研究[J]. 地震工程与工程振动, 2001, 21(1): 94-97.

DENG Minxian, GAO Xiaokang, ZHANG Yongkai. Research on practical method for predicting earthquake damage to underground pipelines[J]. Earthquake Engineering and Engineering Vibration, 2001, 21(1):94-97.

[16] 中华人民共和国石油天然气管道保护法[Z]. 北京: 法律出版社, 2010.

Experiments for effect of blasting vibration on underground pipeline and risk prediction

ZHANG Liming1, ZHAO Mingsheng2,3, CHI En’an1,2, HUANG Bo1, HE Xinggui1

(1. Mining College, Guizhou University, Guiyang 550025, China; 2. Guizhou Xinlian Blasting Engineering Limited Company, Guiyang 550002, China; 3. China University of Mining and Technology, Beijing 100083, China)

To explore the influence of blasting vibration on underground pipelines, the peak particle velocity was used as a criterion of blasting vibration and the strain was used as a criterion of underground pipeline affected by vibration. A TC-4850N blasting vibration measurer and a DH3820 static strain test system were used to monitor the blasting construction of a project. They measured surface vibration signal and the axial and circumferential strain of the pipe. Fitting analysis of peak particle velocity and pipeline strain shows that there is exponential relationship between blasting vibration peak particle velocity and axial and circumferential strain of corresponding underground pipelines. The fitting relationship was combined with the attenuation law of blasting vibration to predict the maximum ground peak velocity that the pipeline can support. The safe distance was 25.25 m. Thus it needs to improve the 50 m prohibiting range in blasting and forecast the safe distance of underground pipeline according to the actual situation.

blasting vibration; peak particle velocity; strain; fitting analysis; safety criterion

国家自然科学基金(51664007)；黔科合高G字[2015]4004；贵州省工业和信息化发展专项基金计划(2015030)；贵州省高层次创新型人才培养黔科合人才(2016)4030号

2016-02-14 修改稿收到日期： 2016-07-01

张黎明 女，硕士生，工程师，1990年生

赵明生 男，博士后，研究员，1982年生

TD235

A

10.13465/j.cnki.jvs.2017.16.038