基于多重重叠技术的振动信号频谱分析方法研究
2017-08-31颜丙生赵俊杰汤宝平
颜丙生, 赵俊杰, 汤宝平
(1. 河南工业大学 机电工程学院, 郑州 450001;2. 重庆大学 机械工程学院, 重庆 400044)
基于多重重叠技术的振动信号频谱分析方法研究
颜丙生1, 赵俊杰1, 汤宝平2
(1. 河南工业大学 机电工程学院, 郑州 450001;2. 重庆大学 机械工程学院, 重庆 400044)
由于具有较小的旁瓣,汉宁、汉明和三角窗常被用于振动信号频谱分析中。但是,加这些窗会导致落在窗边缘的脉冲信号受到抑制而无法被有效检测出来,而脉冲信号中可能含有设备运行重要信息。针对此问题,研究了基于多重重叠技术的振动信号频谱分析方法并提出了相对最大值抽取的多重重叠算法。通过虚拟仿真信号和MFS-MG机械故障仿真试验台实测信号对多重重叠频谱分析方法进行了试验测试。虚拟仿真结果表明:边缘脉冲信号的多重重叠频谱幅值为一般频谱分析方法的8~10倍;试验台故障模拟信号的分析结果同样表明,多重重叠频谱分析方法比一般频谱分析方法更能表现边缘脉冲信号的宽频特征。
多重重叠技术;相对最大值抽取;频谱分析;振动测试
在机械设备故障诊断领域,对采集到的振动信号进行频谱分析能有效的得到系统各频率成分的振动情况[1-2],通过与设备的各故障特征频率成分在正常情况下的表现相对比,能准确判断设备的状态以及相关信息。
在实际设备状态监测或故障诊断过程中发现,采集到的振动信号常常含有边缘性脉冲事件,这些边缘性脉冲事件会体现设备运行过程中出现的突发状况或一些非周期性故障信息,准确检测出这些边缘性脉冲事件,将机械故障信息完整的表现出来对于设备故障诊断领域具有重要意义。传统的频谱分析方法为了尽可能减少频谱泄露,需要对信号进行加窗(如汉宁窗、汉明窗等)处理[3-4],这一过程会造成信号中的边缘性脉冲事件受到严重抑制而无法被有效检测出来[5],因此需要找到其它方法与频谱分析相结合来解决上述问题。
多重重叠技术的应用在国内多见于通讯领域[6],相关算法有FFT重叠相加抗干扰以及重叠加窗抗频域干扰等优化算法[7],主要用来解决扩频信号失真、误码率恶化以及数据加窗引起的信号失真等问题。国外有使用多重重叠技术和FFT来实现快速卷积算法的研究,在振动测试分析领域有利用FFT、频域有限数据段重叠相加和IFFT来解决振动分析中的信号重构问题,另外有关于使用加权多重重叠FFT与不使用多重重叠FFT对信号检测阀值的不同影响的研究[8-10]。这些关于多重重叠技术的相关应用与研究中多使用直接相加或加权相加的方式来处理数据叠加部分。
将多重重叠技术用于振动信号频谱分析中时,如果使用直接相加或加权相加的方式来处理频谱的叠加会造成信号频谱图的严重失真。本课题通过实验进行对比分析后,提出了相对最大值抽取算法来解决频谱的叠加问题。实际测试中发现,通过使用多重重叠技术对信号进行重叠分段然后结合相对最大值抽取算法能有效检测出振动信号中含有的边缘性脉冲事件,最终该算法被应用到某飞机附件试车台振动测试系统中。
1 多重重叠技术原理及算法实现
1.1 一般频谱分析存在的问题
为了使频谱更加光滑,在进行频谱分析前往往需要加窗,由于矩形窗的旁瓣较高,泄露较大,所以一般不加矩形窗。但是用汉宁窗、布莱克曼窗和三角窗等截取信号时,由于这些窗函数的中间值比较大,两端值比较小,会造成被截取信号两端的幅值被严重抑制。如果是稳态信号,对其进行加窗操作不会存在太大问题;如果在稳态信号中有宽频脉冲等暂态信号存在,并且这些暂态信号又落在所加窗信号的边缘时,这些宽频脉冲信号的幅值就会被抑制,在频谱中就可能会被淹没。最终可能造成零星的或间歇性的宽频脉冲信号的损失,而这些边缘性宽频脉冲信号可能携带有一些机械运行过程中的突发状况或潜在隐患信息,如图1所示,原始信号经加窗以后,宽频脉冲基本消失,且频谱分析结果也只含有稳态信号的频谱,宽频脉冲信号所携带的信息被抑制。

图1 信号加窗及频谱分析结果Fig.1 The result of traditional spectrum analysis
1.2 多重重叠技术
多重重叠技术是将信号分段重叠处理的一种方式,包括三个方面:①对被分析的信号要分段;②分段时相邻数据段要有重叠;③分段做频谱后要对频谱分析结果进行叠加。假设被分析信号长度为L,如果直接做频谱,宽频脉冲信号落在窗边缘,杂散事件必将会被抑制,所以必须对被分析信号进行分段;采用不重叠分段的情况下,如果分四段,连续截取首尾相连的信号段,截取后每段信号长度为L/4。如果采用多重重叠分段,重叠率设为50%(可调整),仍然分为4段,每段的长度就是2L/5,要比直接首尾相连分4段每段的长度要长,这样再对每小段信号进行频谱分析,含有宽频脉冲信号的信号段中宽频脉冲信号落在窗边缘的几率变小(分段数合理时信号段重叠率高,宽频脉冲信号落在窗边缘几率越小),重叠分段截取并作频谱分析后,再将这些频谱进行叠加,这样每2L/5段的信息都会综合显示为最终频谱,边缘性杂散信息不会丢失。

图2 多重重叠原理图Fig.2 Diagram of overlap processing
图2为多重重叠分段截取信号的基本原理图,即为对一段信号进行频谱分析时,不是首尾连接的分成四段,而是按一定比例,重叠的分成4段,然后再求四段的叠加频谱。

图3 多重重叠频谱分析信号处理流程图Fig.3 Flow chart of spectrum analysis based on overlap processing
图3为对信号进行多重重叠频谱分析处理流程图,对采集到的信号进行分段(段数可自由设定),其中分段要有重叠,重叠率也可调。然后分段做频谱分析,再将各段的频谱分析结果进行叠加处理,最后输出总的频谱分析结果。
1.2 基于相对最大值抽取算法的多重重叠频谱分析方法
对信号进行分段做频谱后对频谱分析结果进行直接相加或加权相加处理,这是传统的算法,存在如下问题:如果将长度为L的信号被重叠分为4段,信号的中间部分可能被重复截取了4次,但两边的信号只被截取了1次,这样会出现一段信号被做频谱的次数不相同,频谱叠加后的贡献也不同,所以必须想办法还原真实的频谱,还原的算法非常复杂,误差也比较大。根据实际需求提出了基于“相对最大值抽取算法”的多重重叠频谱分析方法。
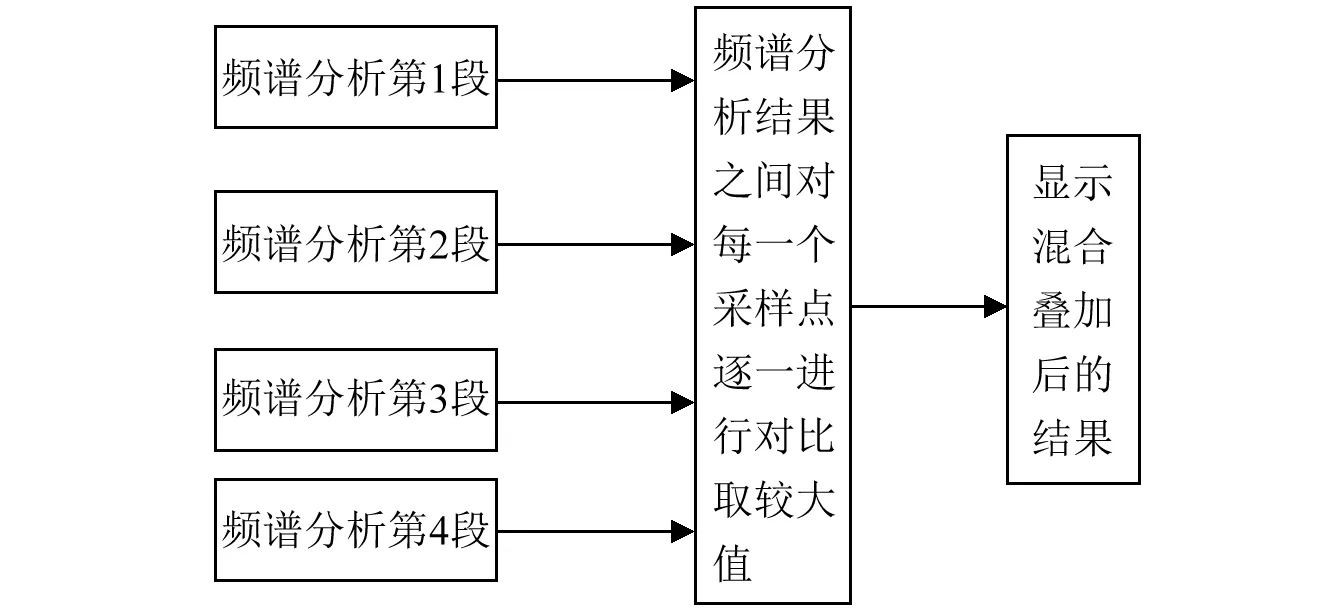
图4 相对最大值抽取算法的技术流程Fig.4 Flow chart of relative maximum extraction algorithm
图4为相对最大值抽取算法的技术流程。核心在于分段做频谱后不再直接对频谱分析结果相加求和或加权相加求和,而是将每段信号频谱进行逐点比较,抽取最大值,最后显示各段综合频谱,宽频脉冲信息的损失必然减少。由于每段的采样率和采样点数相同,每段信号的频谱分析结果的频率范围为采样率的一半,且谱线数相同,这就为频谱的叠加提供了可能。

图5 相对最大值抽取算法的频谱处理示意图Fig.5 Process of spectrum for relative maximum extraction algorithm
图5为相对最大值抽取算法的频谱处理示意图。分段做频谱时,每一段包含不同的信息,将每一段频谱
分析结果进行对比并保留最大值,这样每一段信号的信息都会得到保留。从图5中可知,波形1与波形2是两组不同的频谱分析结果,波形1与波形2重叠之后形成了波形3所示的图形,对重叠的结果进行逐点对比取较大值,得出波形4即多重重叠频谱结果。
1.4 算法实现
图6为基于相对最大值算法的多重重叠功率谱分析程序。其中的“信号段长度”是指:若“信号段长度”值为n,整个信号长度为L,则每次截取到的每一小段信号长度则为L/n,在重叠率为50%时,每次重叠部分的长度则为L/(2n),当对信号段从前往后进行信号截取时,每次截取范围依次为
由以上信号段序列的第一个值可知,对整段信号需要截取的次数为2n-1。因为计算机中的振动信号以离散数据的形式存储的,在进行信号的截取过程中是以采样点数进行分割的,而采样点数均为整数,所以需要对除法计算的结果进行取整操作,程序中使用了向下取整。在利用for循环分别截取了每一小段信号并对其进行功率谱分析之后,对得到的功率谱数组利用“最大值与最小值”以及“索引数组”函数进行逐点对比处理取较大值,最后得到多重重叠功率谱。
2 测试结果
2.1 仿真信号测试结果
为了测试算法的性能,首先利用仿真信号对其进行测试,利用LabVIEW软件内部提供的正弦信号生成函数产生频率为20 Hz,峰-峰值为8的正弦信号,然后用“Sinc信号生成函数”生成一个峰值为50,采样间隔Δt为0.1的信号(Δt越小,主瓣越窄),延迟为60的Sinc信号。将正弦信号和Sinc信号进行如图7所示的幅值叠加操作得到虚拟仿真信号。
其中采样率设置为2 048,采样时间为2 s。在仿真信号时域波形图中可以看到,Sinc信号大致出现在0.25 s处,相对整段信号的2 s来说,位于其前端1/8处,属于采集到的信号的边缘处。

图6 多重重叠功率谱算法程序Fig.6 Program of spectrum analysis based on overlap processing
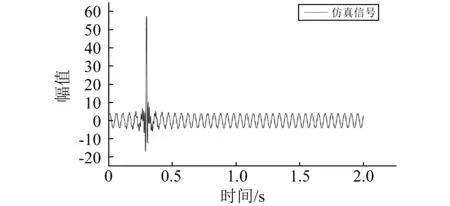
图7 仿真信号Fig.7 Simulation signal
为了验证多重重叠频谱分析方法最终得到的频谱图中确实含有Sinc信号的频谱特征,首先需要分析Sinc信号的频谱特征。对Sinc信号(幅值50、Δt=0.1、延迟101、采样率2 048)单独做幅值谱,其幅值谱结果如图8所示。

图8 Sinc信号幅值谱Fig.8 Amplitude spectrum of Sinc signal
图9为含边缘Sinc仿真信号的一般幅值谱(实线部分)以及多重重叠幅值谱(虚线部分),从图中可以看出,未采用多重重叠算法时,仿真信号在在0~100 Hz的区间内均有频率成分,在20 Hz处分量最大达到2.75,在其他处只有0.1左右,在高于100 Hz的频率成分的幅值谱值基本为0。而在多重重叠幅值谱中,仿真信号中的边缘性Sinc信号幅值谱的值上升到0.9左右,比传统幅值谱分析方法得出的相应值高出了至少8倍,两者对比可以看出传统幅值谱分析中,边缘性Sinc信号的频谱成分受到的抑制非常强。

图9 仿真信号幅值谱Fig.9 Amplitude spectrum analysis of simulation signal
图10为仿真信号的一般功率谱(实线部分)以及多重重叠功率谱(虚线部分)图,从仿真信号的功率谱可以看出,未采用多重重叠算法时,仿真信号只在20 Hz处存在频谱成分,其它频率处的功率谱幅值均为0,仿真信号中的Sinc信号频率成分在进行频谱分析的加窗过程中已经被完全抑制。采用多重重叠功率谱进行分析时,边缘性Sinc信号的功率谱值由之前的0上升到0.85左右,后者比前者至少高出10倍以上。

图10 仿真信号功率谱Fig.10 Power spectrum analysis of simulation signal
通过上述分析可以发现,使用基于相对最大值抽取算法的多重重叠频谱分析方法时,Sinc信号的频谱值基本恢复正常水平,边缘性Sinc信号所携带的频谱信息比传统频谱分析方法得出的频谱信息受到更少的损失,表明基于相对最大值抽取算法的多重重叠频谱分析方法对仿真信号是有效的。
2.2 试验信号测试结果
虽然多重重叠算法用于了某飞机附件试车台振动测试系统中,但在实际运行过程中,出现含边缘性宽频脉冲事件的实例并不常见,且很难人为地在试车台上生成一个含边缘性宽频脉冲事件的振动信号,因此在实验室中利用MFS-MG机械故障仿真试验台模拟试车台运行环境,并对测试系统的算法部分进行测试。
MFS-MG机械故障仿真试验台(如图11)由美国SpectraQuest公司生产,用于各种常见机械故障的模拟。试验中用到的试验台由铝制基座(1.27 cm铸造铝基座,基座加强板,8个橡胶隔振块),电动机(1马力3相电动机,1马力变频交流驱动器),钢制轴(直径1.905 cm,长88.9 cm),2个15.24 cm直径铝制转子以及2个滚动轴承(两侧,间距72.39 cm)。

图11 振动测试台Fig.11 Machine fault simulator (MFS-MG)
试验过程中用到的传感器为ICP加速度传感器(608A11, IMI, 10.6 mV/m/s2), 采集卡为NI 9234采集卡,配套机箱为NI cDAQ-9171 USB接口机箱。
测试过程中为了提高转频的幅值,转子上安装了偏心螺钉,电机转速设置为25 Hz,传感器安装于靠近电机侧的轴承座正上方中央位置,采样频率设置为5 120 Hz,在采集含有边缘脉冲信号过程中,边缘脉冲的产生方式为:利用手持式冲击锤,敲击试验台基座。
固定好传感器并将传感器与数据采集卡利用带屏蔽层的BNC接口线缆连接好,再将数据采集卡的USB接口连上电脑。设置好各项参数并保证盖好试验台的透明防护罩之后,打开MFS-MG机械故障仿真试验台的总电源,在变频器上将电机的目标转速设置为25.1 Hz(实际转速会比目标转速小0.1左右),按下变频器上的“Run”按钮,电机开始运转。待电机运转稳定后,在电脑上的软件端使用自动监测模式(可以根据振动烈度的大小自动存储信号段,振动烈度阈值设置为2)开始对试验台进行状态监测。在试验台运行过程中,利用手持式冲击锤单次敲击暴露在防护罩外的试验台基座边缘部分(在此过程中,软件系统会自动采集超过烈度阈值的信号)。
按上述步骤,分别采集含一次边缘脉冲以及含两次边缘脉冲的故障模拟信号,实际采集到的信号以及对信号的频谱分析结果如图12、图13所示。

图12 含单次边缘脉冲的信号及其频谱分析结果Fig.12 Signal with single edge-pulse and it’s spectrum analysis
图12(a)为振动信号时域波形图,采集到的加速度信号中含有单次边缘脉冲事件;图12(b)为脉冲信号附近0.2 s范围内的信号的幅值谱;图12(c)为振动信号幅值谱,幅值谱结果以转频25 Hz为主,其余频率成分幅值较低;图12(d) 为振动信号多重重叠幅值谱,多重重叠幅值谱结果中除了转频25 Hz频率成分幅值最高,其余频率成分幅值较幅值谱有了明显提高,且在多个宽频范围内保持连续较高幅值;图12(e)为振动信号功率谱,功率谱中只有转频25 Hz的单一频率成分;图12(f)为振动信号多重重叠功率谱,在多重重叠功率谱中除了25 Hz外,在160~260 Hz以及540~640 Hz处保持连续较高幅值,其余频率成分处的幅值也较功率谱有了少量提升。
综合图12中频谱分析结果来看,利用一般频谱分析方法对含有边缘性脉冲成分的振动信号进行频谱分析时,边缘脉冲信号的频谱特征被严重抑制。而使用多重重叠频谱分析方法对信号进行分析时,脉冲信号的频谱幅值得到显著提升,其频谱特征明显改善,在对比分析时,更容易被分辨出来。
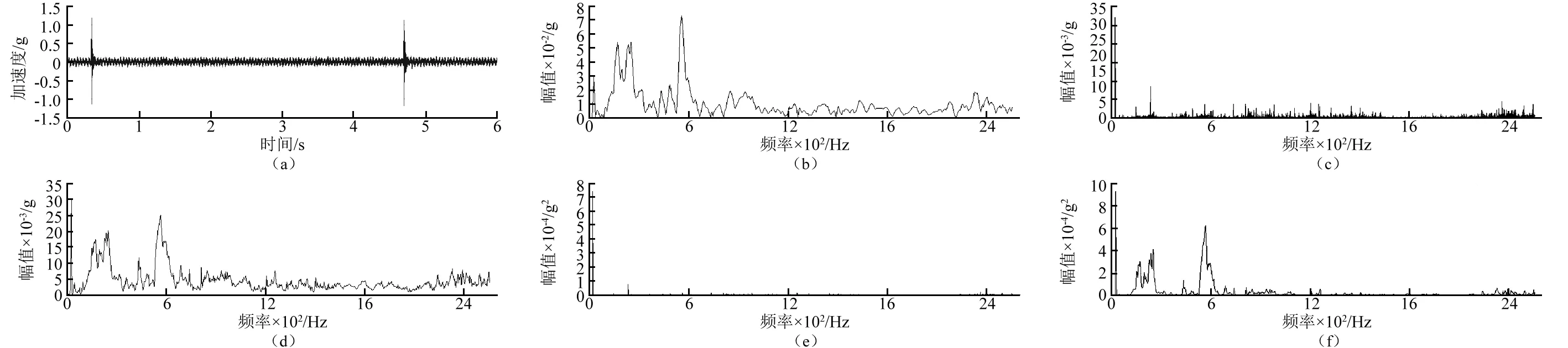
图13 含两次边缘脉冲的信号及其频谱分析结果Fig.13 Signal with two edge-pulse and it’s spectrum analysis
图13(a)为振动信号时域波形图,采集到的加速度信号中含有两次边缘脉冲事件;图13(b)为脉冲信号附近0.2 s范围内的信号的幅值谱;图13(c)为振动信号幅值谱,幅值谱结果以转频25 Hz为主,其余频率成分幅值较低;图13(d) 为振动信号多重重叠幅值谱,多重重叠幅值谱结果中除了转频25 Hz频率成分幅值最高,其余频率成分幅值较幅值谱有了明显提高,且在多个频率范围内保持连续较高幅值;图13(e)为振动信号功率谱,功率谱中只有转频25 Hz的单一频率成分;图13(f)为振动信号多重重叠功率谱,在多重重叠功率谱中除了25 Hz外,在160~260 Hz以及540~640 Hz处保持连续较高幅值,其余频率成分处的幅值也较功率谱有了少量提升。
综合图13中频谱分析结果来看,其结论基本与图12的结论一致。
通过图12、图13的综合分析可以判断,在不使用多重重叠算法的情况下,含有边缘性宽频脉冲事件的信号的频谱分析结果中难以判别系统运行过程中是否产生了边缘性宽频脉冲事件;而使用了多重重叠算法时,特别是在将其与传统频谱分析结果相对比的情况下,含有边缘性宽频脉冲事件的信号其多重重叠频谱分析结果中明显含有宽频成分,可据此判断信号中的边缘杂散脉冲事件,并且算法对于含有多次边缘性宽频脉冲事件的情况同样适用。
另外,在对比分析中可以发现,整段振动信号的多重重叠幅值谱分析结果中,脉冲信号成分的幅值谱的幅值并没有完全达到单独对脉冲信号做幅值谱分析时的幅值高度,这是因为在做多重重叠频谱分析时,脉冲信号并不一定会完全落在被分割信号段的中间位置,所以对其频谱特征还是会存在一定的抑制,通过提高信号段的重叠率可以一定程度上解决这一问题,但是又会带来数据处理时计算量的提升,所以在使用多重重叠算法时应根据实际情况合理选择重叠率的大小。
3 结 论
通过无边缘脉冲的信号与含单次边缘脉冲以及含两次边缘脉冲的信号的频谱分析结果(幅值谱、多重重叠幅值谱、功率谱、多重重叠功率谱的)及其频谱分析结果之间的对比可以发现,基于相对最大值抽取算法的多重重叠频谱分析方法能在保持一般频谱分析结果的基础上,有效地将边缘杂散事件的频谱特征表现出来。将多重重叠技术用于信号的功率谱分析比幅值谱效果更明显,通过和一般频谱分析进行对比分析可以更有效的减少频谱分析中杂散事件的损失。
另一方面,基于相对最大值抽取算法的多重重叠频谱分析技术是一种快速、准确的频谱分析方法,完全区别于传统的重叠后求和或加权求和的多重重叠算法,为多重重叠技术的应用提供了一种可供选择的新方法。
[ 1 ] SAIDI L, ALI J B, FNAIECH F. Application of higher order spectral features and support vector machines for bearing fault sclassification[J]. ISA Transactions,2015,54(1):193-206.
[ 2 ] DOLENC B, BOKOSKI P,. Distributed bearing fault diagnosis based on vibration analysis[J]. Mechanical Systems and Signal Processing,2016,66(67): 521-532.
[ 3 ] SARUHAN H, SANDEMIR S, ÇIÇEK A, et al. Vibration analysis of rolling element bearings defects[J]. Journal of Applied Research and Technology,2014,12(3):384-395.
[ 4 ] 王艳丰,朱靖,滕光蓉,等.航空发动机转子早期裂纹故障振动特征的维谱分析[J].振动与冲击,2015,34(1):88-93.
WANG Yanfeng, ZHU Jing, TENG Guangrong, et al. Dimension spectrum analysis on early cracked fault characters of aero engine rotors[J]. Journal of Vibration and Shock,2015,34(1):88-93.
[ 5 ] TRETHEWEY M W. Window and overlap processing effects on power estimates from spectra[J]. Mechanical Systems and Signal Processing, 2000,14(2):267-278.
[ 6 ] 明建成,祁舒喆.实时频谱分析仪中重叠帧频谱分析技术研究[J].电子测量技术,2013,36(12):32-34.
MING Jiancheng, QI Shuzhe. Study of overlapping frames spectrum analysis techniques in real-time spectrum analyzer[J]. Electronic Measurement Technology, 2013,36(12):32-34.
[ 7 ] 杨凯,邹耘,尹路明.重叠加窗FFT频域抗干扰算法设计[J].测绘科学技术学报,2013,30(3):228-231.
YANG Kai, ZOU Yun, YIN Luming. Design of frequency domain anti-jamming algorithm based on overlap windowed FFT[J]. Journal of Geomatics Science and Technology,2013,30(3):228-231.
[ 8 ] BRINCKER R, BRANDT A. FFT integration of time series using an overlap-add technique[C]// 28th IMAC, A Conference on Structural Dynamics. Jacksonville:IMAC, 2010: 1467-1474.
[ 9 ] WANG S, INKOL R, RAJAN S, et al. A comparison of the normalized detection threshold for the overlapped and non-overlapped FFT summation detectors[C]// 2011 Canadian Conference on Electrical and Computer Engineering. Niagara Falls:IEEE, 2011: 000136-000141.
[10] UCHIDA S, SATO A, INAMORI M, et al. Overlapped FFT scheme with frames of non-continuous samples[C]// 2012 IEEE International Conference on Communication Systems. [S.l.]:IEEE, 2012:90-94.
A study on the spectrum analysis of vibration signals based on overlap processing
YAN Bingsheng1, ZHAO Junjie1, TANG Baoping2
(1. School of Mechanical and Electrical Engineering, Henan University of Technology, Zhengzhou 450001, China;2. College of Mechanical Engineering, Chongqing University, Chongqing 400044, China)
A relative maximum extraction algorithm was put forward and combined with overlap processing method to detect a pulse signal in the edge of a time series. The pulse signal was often suppressed in case of Hanning, Hamming and triangular windows, with a low side-lobe, used in the spectrum analysis of vibration signal processing. However, the pulse signal always contained some important information of a running machine. Signals produced by function generator and a machine fault simulator (MFS-MG) were used in the above signal processing method. It shows that the overlap processing spectrum result of virtual simulation test is about 8 to 10 times to the result from traditional spectrum analysis. And the overlap processing spectrum of a pulse signal produced by the MFS-MG can be unfolded clearly, especially when it is compared with traditional spectrum analysis.
overlap processing; relative maximum extraction; spectrum analysis; vibration test
国家自然科学基金项目资助(U1604134;51541508);河南省科技项目资助(152300410201)
2016-05-17 修改稿收到日期: 2016-09-30
颜丙生 男,博士,讲师,1978年1月生
TH165.3
A
10.13465/j.cnki.jvs.2017.16.034
