摆线钢球行星传动运动分叉特性研究

杨荣刚， 安子军， 姜 威

(燕山大学 机械工程学院，河北 秦皇岛 066004)

摆线钢球行星传动运动分叉特性研究

杨荣刚， 安子军， 姜 威

(燕山大学 机械工程学院，河北 秦皇岛 066004)

为揭示摆线钢球行星传动的非线性动力学行为，建立包括外部激励、啮合副啮合状态及啮合刚度等非线性因素的纯扭转强非线性耦合动力学模型。建立能够描述啮合副所处状态的预紧非线性函数，根据静力学分析获得啮合点静态变形量，建立非线性动力学微分方程组，利用数值分析方法获得系统随压缩量、阻尼系数变化的分叉图，并绘制不同参数下的相图和庞加莱图，研究不同参数对系统分叉特性的影响规律。结果表明：轴向压缩量对系统稳定性影响较大；轴向压缩量和旋转阻尼系数增加，高速运转的系统最终稳定于短周期运动，低速运转的系统最终稳定于准周期运动；阻尼较小时系统在低速状态下的稳定性较高，阻尼较大时系统在高速状态下的稳定性较高。

摆线钢球行星传动；非线性振动；分叉；混沌；准周期

摆线钢球行星传动的无侧隙啮合副使其成为精密传动中非常重要的高性能传动机构，该传动机构具有实时无隙啮合传动、传动效率高、噪声低、结构紧凑、传动比大等优点，在高精密传动应用领域有着非常重要的价值和发展前景[1-2]。

国内外学者对摆线钢球行星传动进行了较深入的研究。文献[3]对摆线钢球行星传动的结构和传动原理进行了阐述，并证明机构传动比为定值。文献[4]分析了曲率半径、压力角等影响机械设计的参数，并获得最优值。文献[5]推导了摆线钢球行星传动的基本设计参数，并通过赫兹理论对摆线槽的强度进行了分析。文献[6]通过一种新的效率计算方法对摆线钢球行星传动的参数进行了计算，设计出了一种新型的等速输出机构，并对输出机理进行了研究。文献[7]建立啮合副两点接触力学模型，推导出机构弹性回差公式，并分析参数对弹性回差的影响。安子军等建立摆线钢球行星传动啮合副两点接触状态下的平移-扭转耦合动力学模型，文献[8]揭示了系统的固有特性，并分析摆线钢球行星传动的主要结构参数对固有频率的影响；文献[9]运用多尺度法对系统进行动力稳定性分析，并利用摄动法计算出系统的稳态响应。

摆线钢球行星传动设计有间隙调解机构，在该机构作用下(输出轴向位移或力)啮合副处于预紧状态，使活齿(钢球)与槽的接触点产生一定的预变形量，以实现工作条件下啮合副的精密传动。目前，尚未有文献对处于预紧状态下的摆线钢球行星传动进行研究。因此，建立预紧状态下的啮合副预紧非线性函数对该传动机构进行研究有一定的意义。借鉴齿轮传动间隙非线性函数[10-12]，建立摆线钢球行星传动啮合副预紧非线性函数。

本文在啮合副处于预紧状态下，建立描述啮合副状态的预紧非线性函数，然后建立系统的非线性动力学微分方程，通过数值分析方法对微分方程进行数值求解，获得系统随压缩量、阻尼系数的分叉图，绘制相图和庞加莱图，分析压缩量、阻尼系数对系统非线性动态特性的影响。

1 动力学模型建立

1.1 扭转振动模型建立

摆线钢球行星传动的结构如图1所示，包括中心盘、减速钢球、行星盘、输入轴、输出轴(盘)、等速钢球和间隙消除机构等。中心盘右侧加工有外摆线槽，行星盘左侧加工有内摆线槽，内外摆线槽轴向重合位置处安装减速钢球，刚球球心位于内、外摆线理论廓线切点处。行星盘右侧与输出轴左侧加工有相同数量的环形槽，环形槽轴向重合位置处安装等速钢球。输入轴偏心段带动行星盘平动，行星盘挤压减速钢球，减速钢球在中心盘摆线槽的限制作用下反推行星盘，使行星盘以较低的转速运动，实现减速。行星盘通过等速钢球将转速等速传递给输出轴，实现转速的等速输出。输出轴受到间隙调节机构的预紧作用，轴向微移动δx，使钢球与槽紧密接触。当δx达到一定值时，摆线钢球传动能够实现无隙啮合传动。

机构各构件减掉输入轴转速ωr，使得各构件转化为定轴转动，输出轴绕O1旋转，减速啮合副钢球与等速啮合副钢球均绕O2旋转，行星盘绕O3旋转。考虑中心盘、减速啮合副钢球、行星盘、输出轴、等速啮合副钢球的旋转自由度，建立如图2、图3所示的摆线钢球行星传动非线性纯扭转动力学模型。脚标1、2i、3、4j、5分别指中心盘、第i个减速钢球、行星盘、第j个等速钢球、输出轴。θ1、θ2i、θ3、θ5、θ4j为中心盘、第i个减速钢球、行星盘、输出轴、第j个等速钢球的角位移，Φ2i=ωt+2π(i-1)/Z2为第i个减速钢球转过角度，Φ1i为第i个减速钢球绕P点转过角度，φj=ωtZ2/Z3+2π/Z4为第j个等速钢球转过角度，Z2为减速钢球数，Z4为等速钢球数，ω为减速钢球绕O2旋转角速度，Rw为等速钢球回转半径。

图2 减速啮合副非线性振动模型Fig.2 Nonlinear vibration model of gear meshing pair

图3 等速啮合副非线性振动模型Fig.3 Nonlinear vibration model of equal meshing pair

1.2 各构件相对位移

在轴向预紧作用下，行星盘相对于中心盘轴向微移动δ1x，根据静力学分析可知，减速啮合副中A1、B2、C1、D1四个啮合点压缩量(预紧量)分别为

(1)

式中：β为减速啮合副啮合点法线与盘平面夹角；kA(Φ2i)、kB(Φ2i)、kC(Φ2i)、kD(Φ2i)为减速啮合副啮合点啮合刚度系数[13]。

设输出轴相对于行星盘轴向微移动δ2x，减速啮合副中A2、D2压缩量相同，B2、C2压缩量相同，啮合点压缩量分别为

(2)

式中：β1、β2为等速啮合副外、内侧啮合点法线与盘平面夹角。

根据行星盘的力平衡条件求解δ1x、δ2x、δx，三者之间的关系为

(3)

其中，

中心盘与第i个减速钢球相对位移量为

δ12i=θ1l1i-θ2il2i

(4)

式中，l1i、l2i分别为O1、O2到法平面的距离。

中心盘与减速钢球之间的预紧非线性函数为f(δ12i)，啮合刚度非线性函数为k12i，则

(5)

行星盘与第i个减速钢球相对位移量为

δ32i=θ3l3i-θ2il2i

(6)

式中，l3i为O3到法平面的距离。

行星盘与减速钢球之间的预紧非线性函数为f(δ32i)，啮合刚度非线性函数为k32i，则

行星盘与第j个等速钢球相对位移量为

δ34i=(θ3-θ4j)l4j

(8)

式中，l4j为回转中心到法平面的距离。

行星盘与等速钢球之间的预紧非线性函数为f(δ34j)，啮合刚度非线性函数为k34j，则

(9)

行星盘与第j个减速钢球相对位移量为

δ54i=(θ5-θ4j)l4j

(10)

输出轴与等速钢球之间的预紧非线性函数为f(δ54j)，啮合刚度非线性函数为k54j，则

(11)

式中，kA、kB、kC、kD为等速啮合副啮合刚度。

减速钢球与中心盘啮合时，摩擦方向系数函数

(12)

摩擦力为

F12i=f12iFf12iμf

(13)

式中：Ff12i为非传力啮合点法向啮合力；μf为滑动摩擦因数，取μf=0.05。

减速钢球与行星盘啮合时，摩擦方向系数函数

(14)

摩擦力为

F32i=f32iFf32iμf

(15)

式中，Ff32i为非传力啮合点法向啮合力。

等速钢球与行星盘啮合时，摩擦方向系数函数

(16)

摩擦力为

F34j=f34jFf34jμf

(17)

式中，Ff34j为非传力啮合点法向啮合力。

等速钢球与输出轴啮合时，摩擦方向系数函数

(18)

摩擦力为

F54j=f54jFf54jμf

(19)

式中，Ff54j为非传力啮合点法向啮合力。

1.3 建立微分方程

根据各构件间的相对位移关系，建立非线性动力学微分方程

(20)

式中：Tr、Tc分别为输入、输出扭矩；J1、J2、J3、J4、J5分别为中心盘、减速速钢球、行星盘、等速钢球、输出盘绕回转中心的转动惯量；c为旋转阻尼系数；Fk12i=k12i×f(δ12i)l1i+F12iL1i；Fk32i=k32if(δ32i)l3i+F32iL3i；Fq12i=k12i×f(δ12i)l2i+F12iL2i；Fq32i=k32if(δ32i)l2i+F32iL2i；Fk34i=k34i×f(δ34i)l4i+F34iL4i；Fk54i=k54if(δ54i)l4i+F54iL4i。

其中，L1i、L2i、L3i、L4i摩擦力作用线到回转中心距离。

1.4 微分方程无量纲化

引入量纲一时间

τ=ωnt

(21)

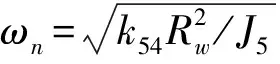
引入角位移标称尺度bc，则量纲一角位移、角速度、角加速度为

(22)

系统量纲一微分方程为

(23)

2 动力学特性分析

中心盘为输入端，输出轴为输出端，扭矩Tr=2 N·m，转动惯量J1、J2、J3、J4、J5分别为3.7×10-4kg·m2、7.1×10-7kg·m2、2.8×10-4kg·m2、7.1×10-7kg·m2、4.5×10-4kg·m2，Z1、Z2、Z3、分别为19、20、21，β、β1、β2均为π/4，短幅系数K为0.4，滚圆半径r0=4 mm，钢球半径rq=1.5 mm。采用数值算法中的变步长Runge-Kutta法(ode45)对非线性方程组进行求解。

2.1 系统随压缩量的分叉特性

取转速ω=10 rad/s，旋转阻尼c=0.05 N·m·s/rad，系统随δx的分叉图如图4所示，相图与庞加莱图如图5所示。随着轴向压缩量增加，系统经短暂混沌运动进入准周期运动，然后经多周期运动进入混沌运动，在δx=5.31 μm处系统由混沌运动突然跃变到准周期运动，跃变后系统稳定于准周期运动状态。系统运动状态的突然跃变呈现典型的激变特征，证明系统是通过“激变”途径进入准周期运动，“激变”途径多发于含间隙系统[14-15]。因此，预紧量较小时，摆线钢球行星传动存在齿侧间隙，预紧量增加啮合副实现无隙啮合传动。

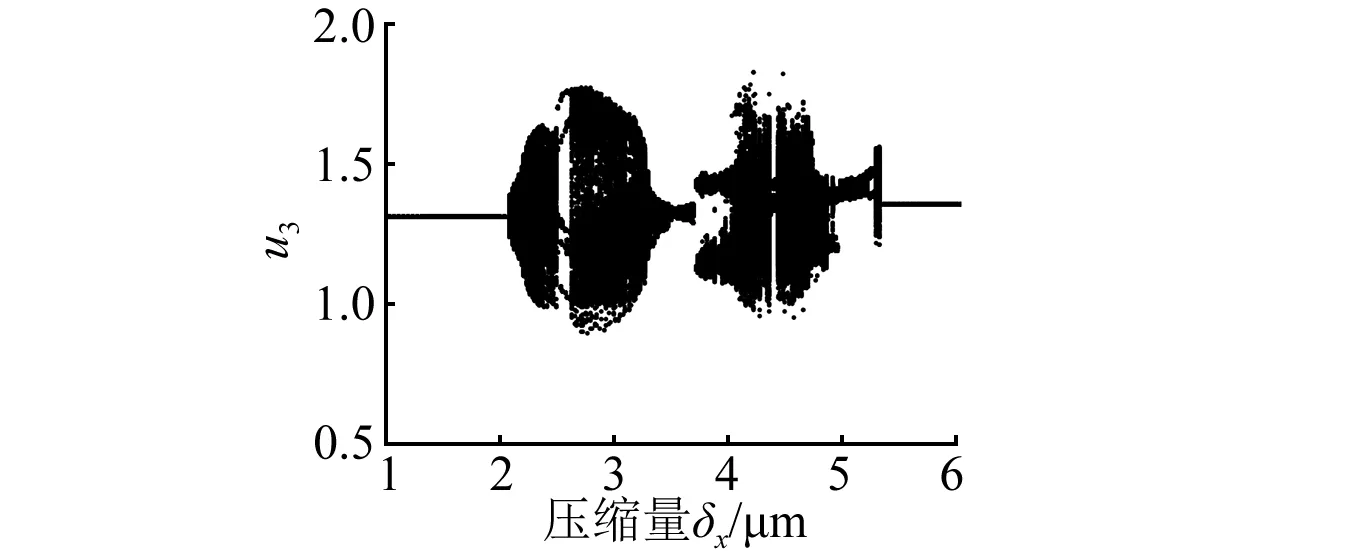
图4 系统随δx变化分叉图Fig.4 Bifurcation diagram of δx

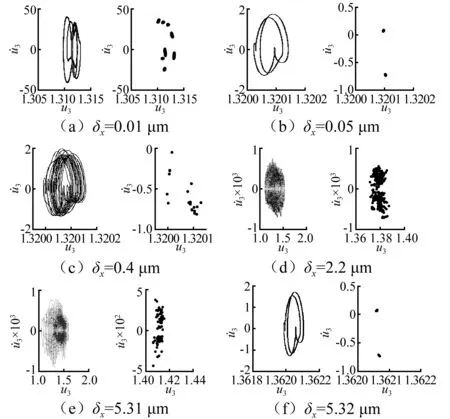
图5 系统相图及庞加莱图Fig.5 Phase diagram and poincare diagram

取转速ω=10 rad/s，扭矩Tm=2 N·m，旋转阻尼c=0.08 N·m·s/rad，系统随δx的分叉图如图6所示，相图与庞加莱图如图7所示。与c=0.05 N·m·s/rad时系统分叉特性相比，该参数下的系统稳定性增强，由混沌运动突然跃变到准周期运动对应的压缩量下降为δx=5.28 μm，其余分叉特性相似。

图6 系统随δx的分叉图Fig.6 Bifurcation diagram of δx

图7 系统相图与庞加莱图Fig.7 Phase diagram and poincare diagram

取转速ω=20 rad/s，旋转阻尼c=0.08 N·m·s/rad，系统随δx的分叉图如图8所示，相图与庞加莱图如图9所示。随着轴向压缩量增加，系统经短暂的混沌运动进入短周期运动，由短周期运动逐渐进入长周期运动，然后进入混沌运动，压缩量δx=5.573 μm时系统由混沌运动突然跃变到短周期运动状态，跃变后系统稳定于短周期运动状态。

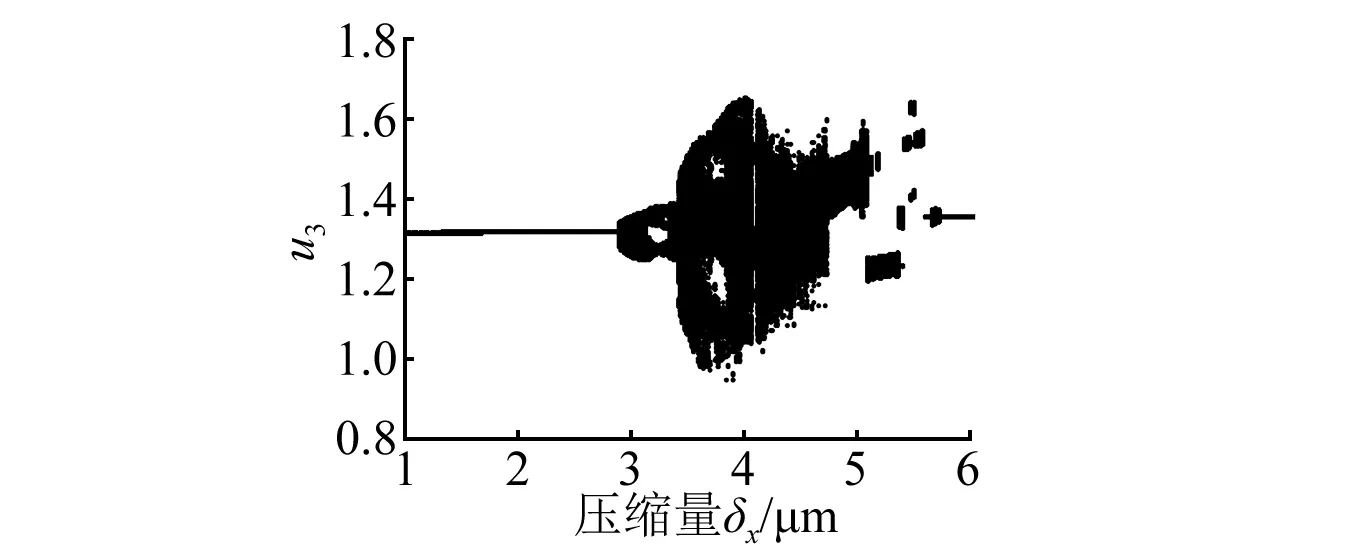
图8 系统随δx的分叉图Fig.8 Bifurcation diagram of δx

图9 系统相图与庞加莱图Fig.9 Phase diagram and poincare diagram

取转速ω=20 rad/s，旋转阻尼c=0.1 N·m·s/rad，系统随δx的分叉图如图10所示，相图与庞加莱图如图11所示。随着轴向压缩量增加，系统经短暂混沌运动进入短周期运动，由短周期运动进入长周期运动，然后经准周期运动进入混沌运动，在准周期运动中会出现短暂的长周期运动，当压缩量δx=5.578 μm时系统由混沌运动突然跃变到短周期运动。跃变后，系统稳定于短周期运动状态。高转速下，阻尼增大，系统的稳定性进一步增强。

图10 系统随δx变化分叉图Fig.10 Bifurcation diagram of δx

图11 系统相图及庞加莱图Fig.11 Phase diagram and poincare diagram

系统处于混沌表明运动状态的不可预知性，由一种轨道突跳到另外轨道上，这种突跳容易使机器疲劳，寿命减短，则机构运行时需要避免混沌运动状态的出现。通过以上分析，可以获得使系统避开混沌运动所需的轴向压缩量取值范围。

2.2 系统随旋转阻尼的分叉特性

系统随旋转阻尼的分叉特性如图12、图13所示，δx=6 μm、ω=20 rad/s时分叉图为图12(a)所示，δx=6 μm、ω=10 rad/s时分叉图为图13(a)所示。

由图12可知，随着阻尼系数增大，系统由混沌运动迅速进入三周期运动，c=0.198 N·m·s/rad时系统经过突变进入双周期运动，c=0.396 N·m·s/rad时系统经过突变进入单周期运动。由图13可知，低转速条件下，随着阻尼系数增大，系统由混沌运迅速进入准周期运动，系统在c=0.082 N·m·s/rad、c=0.398 N·m·s/rad时发生突然跃变，稳定性增强。

3 结 论

在轴向预紧力条件下建立摆线钢球行星传动非线性动力学微分方程，对系统的非线性动力学特性进行了分析，得到如下结论：

图12 系统随c的分叉特性Fig.12 Bifurcation diagram of c

图13 系统随c的分叉特性Fig.13 Bifurcation diagram of c

(1)摆线钢球行星传动在各种非线性因素的综合影响下表现出了非常丰富的分叉特性，随着参数的变化系统出现了短周期运动、长周期运动、准周期运动和混沌运动等运动形态。

(2)传动机构在高速运转状态下，随着轴向压缩量和旋转阻尼系数的增加，系统由混沌运动经过突跳最终稳定于短周期运动；传动机构在低速运转状态下，随着轴向压缩量和旋转阻尼系数的增加，系统由混沌运动经过突跳最终稳定于准周期运动。

(3)轴向压缩量对系统稳定性影响较大，转速对系统稳定性影响较小。阻尼较小时，系统在低速状态下的稳定性较高；阻尼较大时，系统在高速状态下的稳定性较高。阻尼增加，系统稳定性逐渐增强。

[ 1 ] 王国彪，赖一楠，范大鹏，等. 新型精密传动机构设计与制造综述[J]. 中国机械工程，2010,21(16):1891-1897. WANG Guobiao, LAI Yi’nan, FAN Dapeng, et al. Summary of new type precision transmission design and manufacture[J]. China Mechanical Engineering, 2010, 21(16):1891-1897.

[ 2 ] 徐盛林，陈耿. 精密超精密定位技术及其应用[J]. 中国机械工程，1997 ,4:73-75. XU Shenglin, CHEN Geng. Precision ultra-precision positioning technology and its applications[J]. China Mechanical Engineering, 1997,4:73-75.

[ 3 ] TERADA H, MAKINO H, IMASE K. Fundamental analysis of a cycloid ball reducer,(1st report) motion principle[J]. Journal Japan Society for Precision Engineering, 1988, 54: 2101-2106.

[ 4 ] TERADA H, MAKINO H, IMASE K. Fundamental analysis of a cycloid ball reducer,(2st report) motion principle[J]. Journal Japan Society for Precision Engineering, 1990, 56: 751-756.

[ 5 ] TERADA H, MAKINO H, IMASE K. Fundamental analysis of cycloid ball reducer (3rd report)-strength design[J]. Journal Japan Society for Precision Engineering, 1995, 61: 1705-1709.

[ 6 ] TERADA H, MAKINO H, IMASE K. Fundamental analysis of cycloid ball reducer (4th report)-efficiency analysis and development of the Oldham's type output mechanism[J]. Journal Japan Society for Precision Engineering, 1997, 63: 834-838.

[ 7 ] 安子军，杨荣刚，宜亚丽. 精密钢球传动啮合法向力与弹性回差[J]. 机械工程学报，2016, 52(9): 42-48. AN Zijun, YANG Ronggang, YI Yali. Engagement normal force and elastic ball transmission[J]. Journal of Mechanical Engineering，2016, 52(9): 42-48.

[ 8 ] 安子军，张鹏，杨作梅. 摆线钢球行星传动系统参数振动特性研究[J]. 工程力学，2012, 29(3):244-251. AN Zijun, ZHANG Peng, YANG Zuomei. Research on properties for parametric vibration of cycloid ball planetary transmission system[J]. Engineering Mechanics, 2012, 29(3):244-251.

[ 9 ] 张鹏，安子军. 摆线钢球行星传动动力学建模与固有特性分析[J]. 中国机械工程，2014, 25(2):157-162. ZHANG Peng, AN Zijun. Dynamics model and natural characteristics of cycloid ball planetary transmission[J]. China Mechanical Engineering, 2014, 25(2):157-162.

[10] 陈思雨，唐进元，谢耀东. 齿轮传动系统的非线性冲击动力学行为分析[J]. 振动与冲击，2009，28(4)：70-75. CHEN Siyu, TANG Jinyuan, XIE Yaodong. Analysis of nonlinear impact dynam ic behavior for agear pair system with tim e-varying stiffness and friction[J]. Journal of Vibration and Shock，2009，28(4)：70-75.

[11] AL-SHYYAB A，KAHRAMAN A. A non-linear dynamic model for planetary gear sets[J]. Proceedings of the Institution of Mechanical Engineers，Part K-Journal of Multi-body Dynamics，2007，221(4)：567-576.

[12] 孙涛，沈允文，孙智民，等. 行星齿轮传动非线性动力学方程求解与动态特性分析[J]. 机械工程学报，2002，38(3)：11-15. SUN Tao，SHEN Yunwen，SUN Zhimin，et al. Study on nonlinear dynamic behavior of planetary gear train solution and dynamic behavior analysis[J]. Journal of Mechanical Engineering，2002，38(3)：11-15.

[13] HARRIS T A, KOTZALAS M N. Rolling bearing analysis[M].[S.l.]: CRC/Taylor & Francis, 2006.

[14] 李同杰，朱如鹏，鲍和云，等. 行星齿轮传动非线性振动建模与运动分叉特性研究[J]. 机械工程学报，2011，47(21)：76-83. LI Tongjie，ZHU Rupeng，BAO Heyun，et al. Nonlinear torsional vibration modeling and bifurcation characteristic study of a planetary gear train[J]. Journal of Mechanical Engineering，2011，47(21)：76-83.

[15] 冯进钤，徐伟. 碰撞振动系统中周期轨擦边诱导的混沌激变[J]. 力学学报，2011，45(1)：30-36. FENG Jinqian，XU Wei. Grazing-induced chaostic crisis for periodic orbits in vibro-impact systems[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011，45(1)：30-36.

Bifurcation characteristics study of cycloid ball planetary transmission

YANG Ronggang, AN Zijun, JIANG Wei

(School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China)

In order to reveal the nonlinear dynamic behavior of cycloid ball planetary transmission, a pure torsion strengthening nonlinear coupling dynamic model was established and external excitation and meshing pair meshing state and meshing stiffness of the nonlinear factors were included in the model. The nonlinear function of the preload was established to describe the state of the meshing pair. According to the static analysis, the static deformation of the meshing point was obtained, and then the nonlinear dynamic differential equations were achieved., MATLAB was used to obtain the system with pressure shrinking, damping coefficient of variation of the bifurcation diagram and draw different parameters of phase diagram and Poincare map. The effects of different parameters on the bifurcation characteristics of the system were studied. The results show that the axial compression has a great influence on the stability of the system. Increase of axial compression and rotational damping coefficient, the system at high speed operation is stable in short period; the system at low speed operation is stable in the quasi periodic motion. The stability of the small damping system is higher in low speed state and the stability of the high damping system is high in the high speed state.

cycloid ball planetary transmission; nonlinear vibration; bifurcation; chaos; quasi period

国家自然科学基金资助项目(51275440)；河北省自然科学基金资助项目(E2013203085)

2016-07-20 修改稿收到日期： 2016-11-22

杨荣刚 男，博士生，1988年8月生

安子军 男，博士，教授，博士生导师，1960年2月生

TH113.1

A

10.13465/j.cnki.jvs.2017.16.021