热连轧机机液耦合动力学系统控制参数优化

凌启辉， 赵前程，王 宪，王肖芬

(湖南科技大学 机电工程学院，湖南 湘潭 411201)

热连轧机机液耦合动力学系统控制参数优化

凌启辉， 赵前程，王 宪，王肖芬

(湖南科技大学 机电工程学院，湖南 湘潭 411201)

以现场某热连轧机机液耦合系统为研究对象，提出一种基于双目标改进粒子群优化热连轧机机液耦合系统控制参数并控制其振动的方法。通过建立热连轧机机液耦合系统动力学模型，以热连轧机机液耦合系统响应指标最佳和振动强度最弱为目标函数，对液压压下系统控制参数进行优化，获得了在满足系统动态响应要求的前提下其振动最小的最优控制参数；通过数值计算得到系统在不同控制参数下的振动加速度有效值和动态响应，仿真结果表明系统振动最小时其动态响应指标达不到要求，而响应指标最优时系统振动较大。将优化方法应用于工业现场轧机，实践证明，调整轧机液压压下系统控制参数后可有效缓解轧机振动大小，为抑制热连轧机振动提供了有效的解决途径。

热连轧机；机液耦合；粒子群；目标函数；优化

轧机振动在轧制领域一直备受关注。随着市场竞争力及带钢产品消费结构变化，带钢轧制生产有以热轧代替部分冷轧的发展趋势，在轧制薄规格、高强度带钢时，热连轧机呈现出复杂的多种现象并存的振动，表现为“幽灵”式振动[1-2]。由于液压伺服技术的广泛应用，厚度自动控制的发展，薄带产品质量要求的提高及其加工难度的增大，轧机机液耦合系统动力学特性研究逐渐进入学者的视野[3-4]。

液压压下系统的可靠运行是整个轧钢生产线正常化生产的保证。由于液压压下系统是机电液一体化的综合系统，系统中任一部件的参数设计不合理都可能导致整个系统产生振动[5]。轧机振动使带钢表面出现振纹，导致带钢厚度公差超出允许范围，而且会在工作辊表面产生振纹，进而加剧振动，影响后续轧制[6]。严重时还会导致堆钢和断带等事故，大大影响设备效能的发挥和连续生产[7]，造成企业经济损失，成为热连轧机生产的瓶颈。生产实践表明，如需轧制较高质量的产品，理想的动力学特性非常重要[8]。

目前，关于轧机振动控制已有学者开展了许多的研究工作并取得了很好的成绩。如韩东颖等[9]为了实现板带轧机机电传动系统给定速度信号跟踪非脆弱控制，设计了前馈补偿器，实现了其扭振控制。但关于轧机液压压下系统的研究重点仍主要集中在液压压下系统控制性能上[10-11]，主要关心系统响应速度和控制精度。如Li等[12]对BISRA-AGC的控制思想和控制模型进行了分析，并提出相应的改进方法，有效提高了厚度控制的控制精度。本文拟通过建立热连轧机机液耦合系统动力学模型，揭示液压压下系统控制参数对轧机辊系振动的影响规律，优化其控制参数，为控制其动力学行提供有效依据，进而提高轧制效率和产品质量。

1 轧机机液耦合系统动力学模型

建立轧机机液耦合系统动力学仿真模型是轧机液压压下控制系统数值仿真分析的基础，也是控制参数优化设计的依据和研究轧机动力学特性的重要手段[13]。因此，本文将轧机机液耦合动力学系统分为轧机辊系、伺服控制系统、非对称液压缸系统和补偿控制系统等四个子系统，其中后面三个子系统统称为液压自动厚度控制系统。

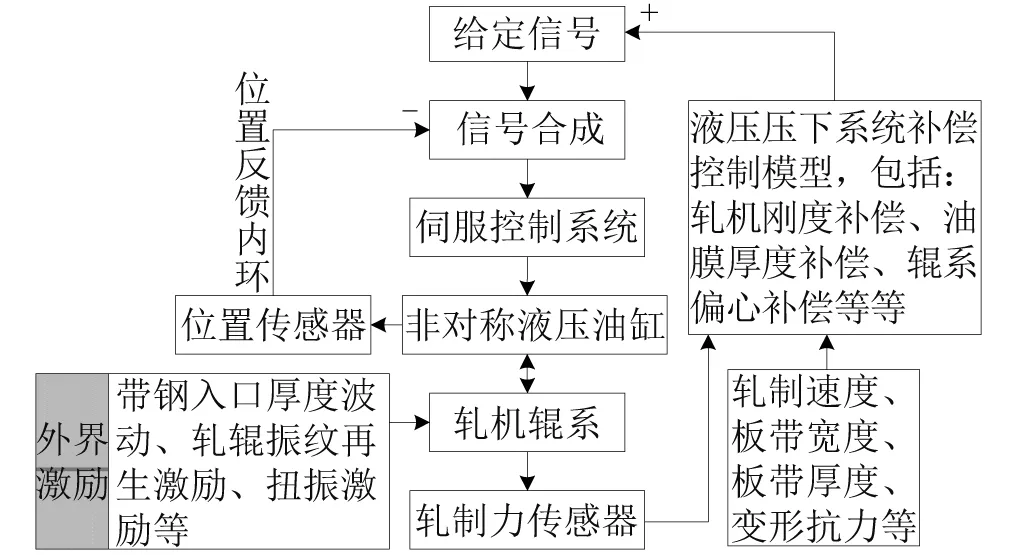
图1 热连轧机机液耦合系统原理示意图Fig.1 Diagram of hydraulic-mechanical coupling system

图1为热连轧机机液耦合系统原理示意图，轧机辊系发生振动时，将造成轧机辊缝和轧制力发生波动，位置传感器(磁栅尺)将测得的辊缝反馈给伺服控制系统，同时轧制力传感器将测得的轧制力信号作用于补偿控制模型，进而反馈给伺服阀给定信号。随后液压压下伺服控制系统也开始通过控制器、伺服阀控制液压缸的输出，从而影响辊缝的变化。

热连轧机机液耦合动力学系统建模方法可参考文献[14]，其建模过程不再详细阐述。本文采用Matlab /Simulink模块化建模方法，建立热连轧机机液耦合系统动力学仿真模型(见图2)。图2中(1)为液压压下系统输入；(2)为PI控制器；(3)为伺服阀模型；(4)为非对称液压缸模型选择开关；(5)为非对称液压缸模型；(6)为轧机辊系模型；(7)为系统输出响应；(8)为波动轧制力计算模型；(9)为补偿控制模型。其中轧机辊系简化为四自由度动力学模型；伺服控制系统主要采用PI控制；非对称液压缸系统压下和抬起时，其模型的表征不一样，简化为液压缸压下模型和液压缸抬起模型，且在这两个模型的前端加入模型开关选择器；补偿控制系统主要包括油膜厚度补偿模型、变刚度补偿模型和动态轧制力计算模型等。轧机辊系、非对称液压缸系统和补偿控制系统采用S-function函数编程建模方法，而伺服阀系统采用传递函数建模方法。同时，图2提供了粒子群优化算法程序的数据接口，以便粒子接入到仿真模型中，仿真后的数据输入到Matlab的数据空间中，方便优化程序计算适应度值。

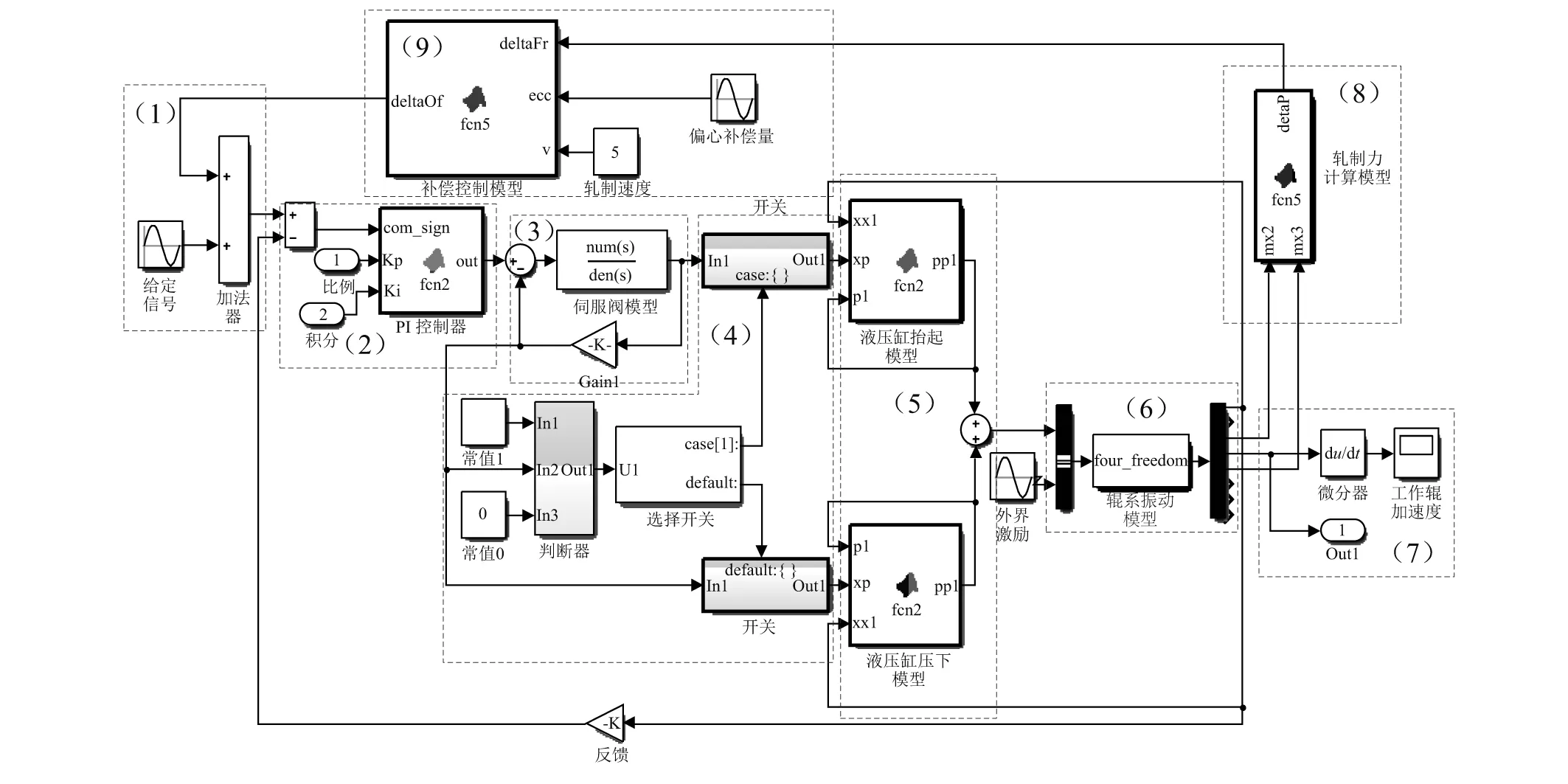
图2 机液耦合系统动力学仿真模型Fig.2 Hydraulic-mechanical coupling system dynamic simulation model

2 基于双目标改进粒子群优化方法

2.1 改进的粒子群算法

标准的粒子群算法可以解决一些问题，但也存在一定的问题。为了改善标准粒子群算法的收敛速度和提高种群多样性，文中在两方面对标准粒子群进行了改进，形成了改进的粒子群算法(Improved Particle Swarm Optimization，IPSO)。

(1) 惯性权重系数的改进

由于权重系数对粒子群算法的影响较大[15]。为了平衡POS算法的全局搜索能力和局部改良能力，本文采用一种权重因子随粒子的目标函数值而自动改变的自适应权重的PSO算法。当各粒子的目标值趋于一致或趋于局部最优时，惯性权重系数增大，则有利于跳出局部最优，进行全局搜索；当各粒子的目标值比较分散时，惯性权重系数减小，则有利于局部搜索，加强算法的收敛。自适应权重系数计算公式为

(1)

式中：ωmin、ωmax分别为ω的最小值和最大值；F为粒子当前的目标函数值；Favg、Fmin分别为当前所有粒子的平均目标值和最小目标值。

(2) 增加收缩因子

学习因子决定了粒子的运行轨迹，反映了粒子群之间的信息交流。设置较大的值，会使粒子过多地在局部范围内徘徊；而较大的值，则又会促使粒子过早收敛到局部最小值。为了改善上述问题，本文采用收缩因子，通过合理选取参数，确保粒子群算法的收敛性，并可取消速度的边界限制，使算法达到全局探测与局部开采间的有效平衡。构造收缩因子的公式为

vi=φ{vi(t)+c1r1[pi-xi(t)]+c2r2[pg-xi(t)]}

(2)

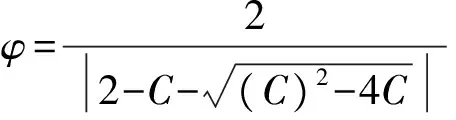
2.2 双目标适应度函数设计及求解过程

(1) 为了获取满意的动态特性，采用系统输出误差绝对值时间积分性能指标作为参数选择的最小目标函数；为了防止控制能量过大，在目标函数中加入控制输入的平方项；为了避免超调，采用了惩罚控制，即一旦产生超调，将超调量作为最优指标的一项[16]。此时，目标函数可设计为

(3)

式中：a1、a2和a3为权值， 取a1=0.999，a2=0.001，a3=100；e(t)为系统的误差；u(t)为系统输出位移响应。

为便于分析研究，将式(3)定义为目标函数一。

(2) 为了得到满意的动力学特性，使得系统振动最小。本文用加速度有效值描述系统的振动大小，加速度有效值可按式(4)计算得到

(4)

式中：n为系统输出位移经两次数值求导后得到的数据个数；xA为加速度。

故，系统振动最小的目标函数可设计为

(5)

此时，将式(5)定义为目标函数二。故系统存在两个目标函数，目标之间相互冲突，优化结果并不一定存在唯一的全局最优解[17]，其特点为至少存在一个目标优于其它所有的解，这样的解称之为非支配解或Pareto解，这些解的集合即为Pareto最优解集。当Pareto最优解集求出来之后，还需要根据设计者的偏好挑选出最后的折衷解或者最优解。为了使各个目标函数尽可能小，可以先分别求出各目标函数的最小值，然后让各目标尽量接近各自的极小值来获得原来问题的解。可以采用如下函数定义和理想解的距离值[18]。

(6)

因此，本文基于双目标的改进粒子群优化系统控制参数方法流程如图3所示。

2.3 算例分析

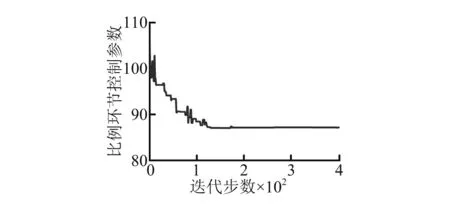
根据上文所选择的目标函数，以某热连轧F3轧机机液耦合动力学系统为研究对象，应用Matlab编写优化程序，结合图2所示系统动力学模型，来实现该系统控制参数的优化，以达到系统振动响应最小和动态过程最佳目的。图4为比例环节控制参数的优化结果，图4(a)为考虑系统振动最小和动态指标最佳时比例控制参数变化曲线，图4(b)为只考虑系统动态响应指标最佳的优化结果，图4(c)为只考虑系统振动最小的优化结果。从图中可看出，只考虑系统动态响应指标时，比例控制参数最佳优化值为4.06；只考虑系统振动响应最小时，比例控制参数最佳优化值为88.21；同时考虑系统振动响应最小和动态响应指标最佳时，比例控制参数最佳优化值为16.13。

图3 粒子群优化方法流程图Fig.3 Particle swarm optimization algorithm flow chart

(a) 双目标函数

(b) 目标函数一

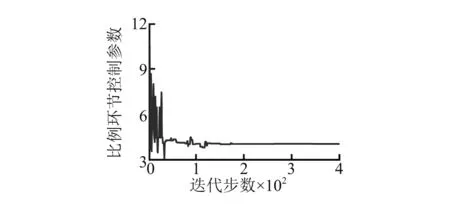
(c) 目标函数二图4 比例环节控制参数优化对比Fig.4 Contrast of proportion link control parameter optimization

图5为积分环节控制参数的优化结果，曲线1为考虑系统振动最小和动态指标最佳时比例控制参数变化曲线，曲线2为只考虑系统动态响应指标最佳的优化结果，曲线3为只考虑系统振动最小的优化结果，其优化结果分别为：0.29、0.16和0.083。从这两幅图可以看出，在考虑系统振动和动态响应指标的情况下，比例控制参数选取16.13，积分控制参数选取0.29最为合适。

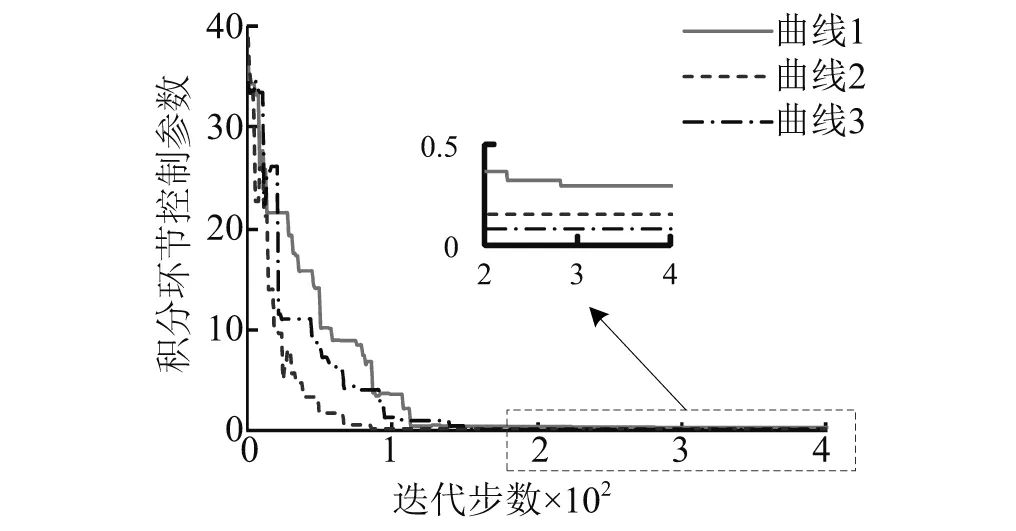
图5 积分环节控制参数优化对比Fig.5 Contrast of integral link control parameter optimization

图6为轧机机液耦合系统在阶跃信号作用下的动态响应，曲线1为考虑系统振动最小和动态指标最佳时的阶跃响应曲线，曲线2为只考虑系统动态响应指标最佳的阶跃响应曲线，曲线3为只考虑系统振动最小的阶跃响应曲线。图6可以看出：①曲线1的动态响应指标虽不是最佳，系统振动不是最小，但能满足系统动态响应要求且此时系统的振动最小；②曲线2的动态响应曲线优于曲线1和曲线3；③曲线3的超调量和调整时间等动态响应指标最差。由此可见，以上结论和上文的优化结果相吻合。

图6 系统阶跃响应Fig.6 System step response

3 基于控制参数变化的系统动力学特征

前面分析可知，控制参数可影响系统的振动大小，下面来讨论随着控制参数的变化，系统的振动情况。

图7为系统振动加速度有效值随比例控制参数变化曲线；图8为系统振动加速度有效值随积分控制参数变化曲线。从图7和图8中可以发现，比例控制参数取90左右时，系统振动加速度有效值最小，积分控制参数在0.01～10，系统振动加速度有效值最小，与前面优化结果相吻合。

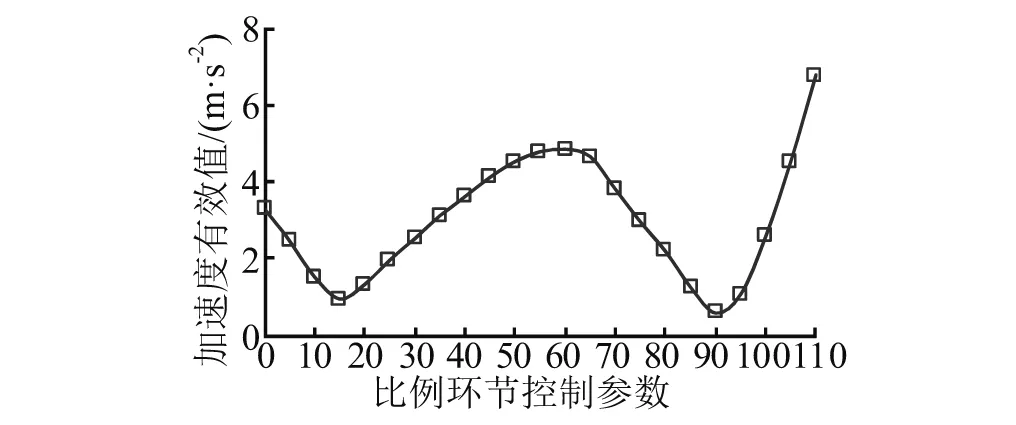
图7 系统加速度随比例控制参数变化曲线Fig.7 System acceleration curve with the variety of the proportional control parameter

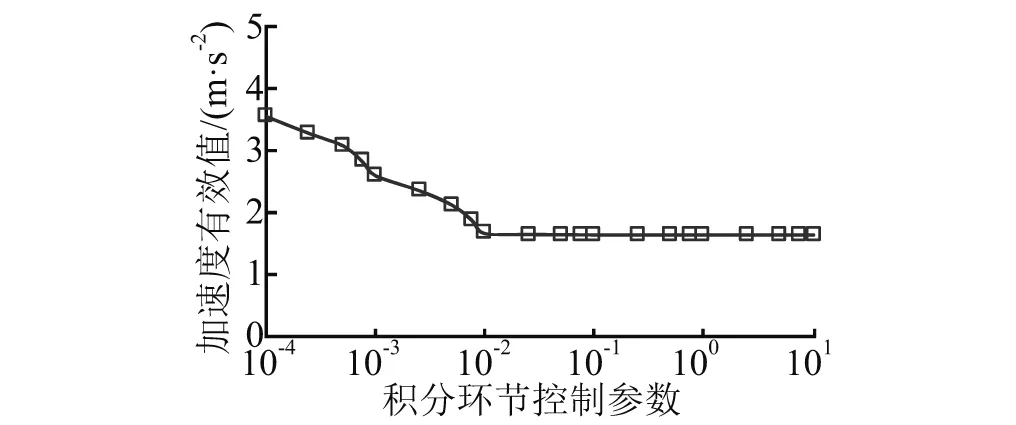
图8 系统振动加速度随积分控制参数变化曲线Fig.8 System acceleration curve with the variety of the integral control parameter

4 工业现场验证

针对现场某热连轧F3轧机在轧制薄规格、高强度带钢时发生强烈振动现象，根据控制参数优化结果，在满足系统动态响应特性的前提下，调整液压压下系统伺服控制参数。在轧制整块高强度合金薄带时，轧机上工作辊垂直方向振动加速度波形如图9所示，图9(a)为控制参数优化前上工作辊振动加速度波形，图9(b)为控制参数调整后上工作辊振动加速度波形，图中信号在开始时间和结束时间振动非常明显，这两个时间点的振动信号分别为咬钢冲击和抛钢冲击，本文不考虑其振动影响。对图9中的加速度数据进行处理，不难发现：①控制参数调整前，轧机系统振动明显，主要发生在整个轧制过程的后半段；②控制参数调整后，轧机系统振动明显减弱；③整个轧制过程的振动加速度有效值从1.63 m·s-2降低到0.80 m·s-2，下降率为50.92%；④振动最强的1 s时间内，振动加速度有效值从2.93 m·s-2降低到0.92 m·s-2，下降率为68.60%。

F3轧机液压压下系统伺服阀给定电流信号波形如图10所示，图10(a)为控制参数调整前伺服阀给定电流信号波形，图10(b)为控制参数调整后伺服阀给定电流信号波形。从图10中可以看出：①控制参数调整前，轧机液压压下系统伺服阀电流信号在整个轧制过程的后半段振荡厉害，这与轧机工作辊振动情况类似；②控制参数调整后，轧机液压压下系统伺服阀电流信号振荡较小，且明显趋于稳定。

图9 工作辊振动加速度Fig.9 Work roll acceleration

图10 伺服阀给定电流Fig.10 Servo given current

对图10中咬钢时刻的伺服阀电流信号进行放大，得到如图11所示的液压压下系统伺服阀给定电流信号的咬钢冲击，图11(a)为控制参数调整前伺服阀给定电流信号波形，图11(b)为控制参数调整后伺服阀给定电流信号波形。从图11中可以看出，控制参数调整前，轧机液压压下系统伺服阀电流信号在咬钢后很快趋于平稳，而控制参数调整后，轧机液压压下系统伺服阀电流信号的动态响应指标稍逊于参数调整前的动态响应指标，但完全可以满足系统的响应要求，这与数值仿真的结果相吻合。

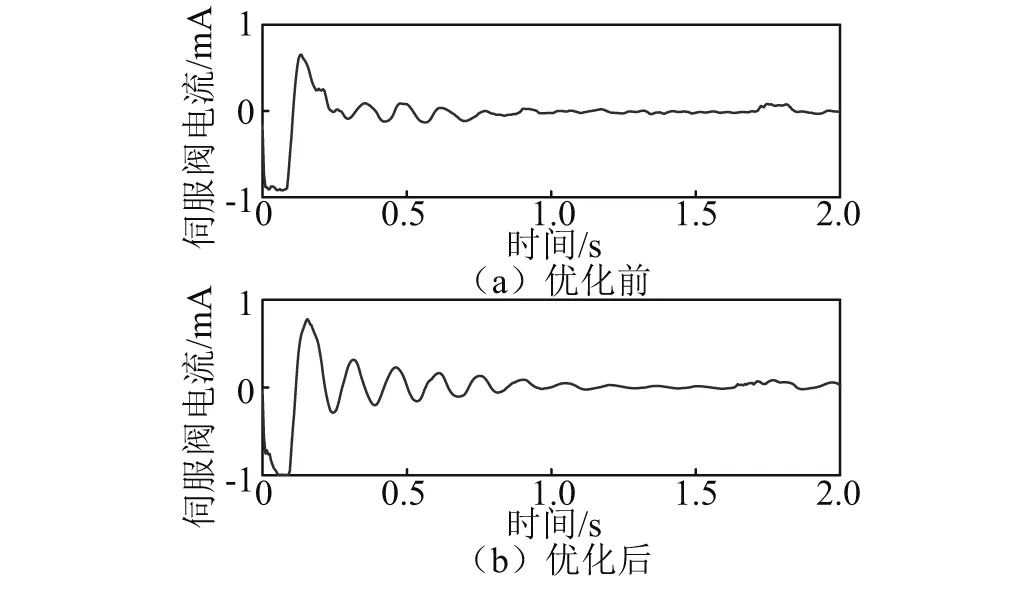
图11 伺服阀给定电流Fig.11 Servo given current

5 结 论

(1) 以现场某热连轧F3轧机机液耦合系统为研究对象，建立热连轧机机液耦合动力学模型，以系统动态响应指标最佳和振动强度最小为目标函数，改进粒子群算法优化其控制参数，在满足动态响应要求的前提下系统振动最小的最优比例控制参数为16.13，而积分控制参数选取0.29最为合适。

(2) 通过数值计算得到系统在不同控制参数下的振动加速度有效值和动态响应，仿真结果表明液压压下系统比例控制参数为90左右时系统振动最小，但其动态响应指标达不到要求，而动态响应指标最优时系统振动较大。

(3) 将优化结果应用于工业现场轧机，调整轧机液压压下系统控制参数后可有效缓解轧机振动大小，仿真和实践结果均表明，证明该方法能很好的控制系统的动力学特性。

[ 1 ] PENG K X，ZHANG K，DONG J，et al．A new data-driven process monitoring scheme for key performance indictors with application to hot strip mill process[J]．Journal of Franklin Institute，2014，351(9)：4555-4569．

[ 2 ] KAPIL S，EBERHARD P，DWIVEDY S K，et al．Nonlinear dynamic analysis of a parametrically excited cold rolling mill[J]．Journal of Manufacturing Science & Engineering，2014，136(4)：10-19．

[ 3 ] 闫晓强．热连轧机机电液耦合振动控制[J]．机械工程学报，2011，47(17)：61-65． YAN Xiaoqiang．Machinery-electric-hydraulic coupling vibration control of hot continuous rolling mills [J]．Journal of Mechanical Engineering，2011，47(17)：61-65．

[ 4 ] 高峰，郭为忠，宋清玉，等．重型制造装备国内外研究与发展[J]．机械工程学报，2010，46(19)：92-107． GAO Feng，GUO Weizhong，SONG Qingyu，et al．Current development of heavy-duty manufacturing equipments [J]．Journal of Mechanical Engineering，2010，46(19)：92-107．

[ 5 ] 姚爱英，熊晓燕，王然风，等．大型带钢轧机动态特性分析与动力学修改[J]．振动、测试与诊断，2012，34(4)：680-684． YAO Aiying，XIONG Xiaoyan，WANG Ranfeng，et al．Dynamic performance analysis and dynamics modification of large strap rolling mills[J]．Journal of Vibration， Measurement &Diagnosis，2012，34(4)：680-684．

[ 6 ] 凌启辉，闫晓强，张清东，等．双动力源驱动下的热连轧机振动特征[J]．振动测试与诊断，2014，34(3)：534-538． LING Qihui，YAN Xiaoqiang，ZHANG Qingdong，et al．Research on vibration characteristics of the hot rolling mill by dual power source driven[J]．Journal of Vibration，Measurement & Diagnosis，2014，34(3)：534-538．

[ 8 ] YAN Xiaoqiang，SUN Zhihui，CHEN Wei．Vibration control in thin slab hot strip mills[J]．Iron making and Steelmaking，2011，38(4)：309-313．

[ 9 ] 韩东颖，时培明，赵东伟，等．板带轧机机电传动系统参激非线性扭振鲁棒控制研究[J]．振动与冲击，2016，35(12)：1-7． HAN Dongying，SHI Peiming，ZHAO Dongwei，et al．Study on robust control for parametric excitation nonlinear torsional vibration of a strip-rolling mill’s mechanical and electrical drive system[J]．Journal of Vibration and Shock，2016，35(12)：1-7．

[10] SUN Jie，ZHANG Dianhua，LI Xu，et al．Smith prediction monitor AGC system based on fuzzy self-tuning PID control[J]．Journal of Iron and Steel Research， 2010，17(2)：22-26．

[11] SUN Shufang，ZHANG Jiahai，WANG Jianhui，et al．The application of new adaptive PSO in AGC and AFC combination control system[J]． Procedia Engineering，2011，16(4)：702-707．

[12] LI Xu，ZHANG Haoyu，ZHANG Jin，et al．Influences to system and superiority of model parameters in dynamic setting AGC[C]// 2011 International Conference on Physics Science and Technology：Physics Procedia. [S.l.]：ICPST， 2011：565-570．

[13] 马维金，李凤兰，王俊元，等．热连轧机磁栅尺结构的模型参数辨识[J]．振动、测试与诊断，2010，30(6)：646-649． MA Weijin，LI Fenglan，WANG Junyuan，et al．Modeling system identification of roller gap displacement sensor structure of hot rolling mill[J]．Journal of Vibration，Measurement &Diagnosis，2010，30(6)：646-650．

[14] 凌启辉．现代热连轧机液机耦合振动研究[D]．北京：北京科技大学，2014：38-74．

[15] KANCHANA S，WORAYA N．Multi-objective particle swarm optimization for mechanical harvester route planning of sugarcane field operations[J]．European Journal of Operational Research，2016，252(3)：969-984．

[16] 王唯一，张明泉，杨帆，等．基于粒子群算法的PID调速系统的研究[J]．控制工程，2015，22(6)：1082-1086． WANG Weiyi，ZHANG Mingquan，YANG Fan，et al．Study of PID speed controller based on particle swarm optimization[J]．Control Engineering of China，2015，22(6)：1082-1086．

[17] 陈玲娟，蒲云．基于粒子群算法的双目标可靠性网络设计[J]．交通运输工程学报，2010(5)：61-65． CHEN Lingjuan，PU Yun．Dual-objective reliable network design based on particle swarm optimization[J]． Journal of Traffic and Transportation Engineering，2010(5)：61-65．

[18] 侯磊．基于多目标粒子群算法的船舶主尺度优化设计研究[J]．船舶力学，2011，15(7)：784-790． HOU Lei．Application of multi-objective particle swarm optimization(MOPSO) in study of ship’s principal parameters[J]．Journal of Ship Mechanics，2011，15(7)：784-790．

Control parameter optimization of a hydraulic-mechanical coupling system of hot strip tandem mill

LING Qihui， ZHAO Qiancheng， WANG Xian， WANG Xiaofen

(College of Mechanical and Electrical Engineering, Hunan University of Science and Technology， Xiangtan 411201， China)

Take a hydraulic-mechanical coupling system of industrial field hot strip tandem mill as the research object， a vibration control method was put forward to optimize control parameters based on an dual target of improved particle swarm optimization. First the hydraulic-mechanical coupling system dynamic model was established， and took the best system response index and the weakest vibration intensity as the objective function， to optimize the hydraulic pressure system control parameter and obtain the optimal control parameters. The relation curve of the control parameters with the vibration acceleration effective value and dynamic response were described using a numerical analysis method. The simulation results show that the system dynamic response index cannot meet the requirements with minimum vibration， and the system dynamic response index is optimal while system vibration is strong. Finally the results of optimization were applied to the industrial field mill. It proves that the adjustment control parameters of the hydraulic pressure down system can effectively alleviate system vibration， which provides effective solution to curb hot strip tandem mill vibration.

hot strip tandem mill； hydraulic-mechanical coupling； particle swarm optimization； objective function； optimization

国家自然科学基金(51505142)

2016-04-06 修改稿收到日期： 2016-06-22

凌启辉 男，博士，讲师，1986年3月生

赵前程 男，博士，教授，1969年11月生

TH113.1

A

10.13465/j.cnki.jvs.2017.16.012