基于前后向子分段和频移补偿的频率与相位联合估计器

黄翔东, 靳旭康, 白瑞朋

(天津大学 电气自动化与信息工程学院， 天津 300072)

基于前后向子分段和频移补偿的频率与相位联合估计器

黄翔东, 靳旭康, 白瑞朋

(天津大学 电气自动化与信息工程学院， 天津 300072)

频率估计和相位估计是物理学中的两个基本的测量问题。现有的估计器难以对这两个参数实现高精度的联合测量。为实现联合测量，对已有前后向子分段频率估计器做如下两方面改进：①对前、后向子分段快速傅里叶变换(Fast Fourier Transform, FFT)谱峰相位值做平均，获得中心样点的瞬时相位估计；②引入频移补偿措施，使得前、后向子分段的峰值谱能量更为集中，增强了估计器抵御噪声的能力，同时提升了估计器的频率和相位估计精度。理论分析和仿真实验表明，该联合估计器性能高于原有前后向子分段估计器和全相位FFT/FFT相位差估计器，对于频率偏离情况，其频率估计方差为克拉美-罗限的4/3倍，其相位估计方差可达到克拉美-罗限。

联合估计器；频率估计；相位估计；频移补偿

频率估计和相位估计是两个基本的测量问题。许多物理量测量可转化为频率估计问题，如大气动力学中的雷达风速测量[1]、阵列信号处理中的波达方向估计[2]、振动分析中的转速测量[3]等；同样地，许多物理量测量可转化为相位测量问题，如通信中的载波同步[4]、电网并网[5]、锁相环电路的实现[6]等。更重要的是，频率测量和相位测量常常不是孤立的，而是需同时实现的。如雷达、声纳系统中，通过测量接收信号的多普勒频移[7]可估计运动目标速度，而通过测量发送信号和接收信号的相位差，则可估计运动目标与发送设备(如雷达)的距离等[8]，因而迫切需设计出可同时实现(而不是单一实现)频率和相位两个参数测量的联合估计器。

然而，当前的研究仍以单一的频率估计器或相位估计器为主，联合估计器的研究较少。各种基于内插的估计器，如Rife估计器[9]、Candan估计器[10]、AM估计器[11]、Macleod估计器[12]，仅涉及频率估计问题，没涉及相位估计问题；而常用的相位测量法(如希尔波特变换法[13]、相关法[14])，仅仅涉及相位估计，没涉及频率估计。需注意的是，频谱校正是实现频率、相位联合估计的有效手段[15-17]，但文献[18]指出：频谱校正的相位估计存在一个缺陷，即相位估计需要从频率估计的结果得到，这样会把频率估计误差传递到相位估计中去，因而会降低精度。

文献[19]提出全相位FFT(all-phase Fast Fourier Transform, apFFT) /FFT相位差频谱校正法，实现了频率、相位的联合估计，文献[20]指出apFFT测相不依赖于频率估计，该测相符合的是幅值、相位未知的两参数估计模型，而不是频率、幅值、相位未知的三参数估计模型，故对应更低的克拉美-罗限(Cramer-Rao lower Bound, CRB)。然而，apFFT的测相方差与该理论下限仍存在一定距离。因而设计出更逼近两参数模型的克拉美-罗限的相位估计器是急需完成的工作。

文献[21]提出了前后向子分段频率估计法，该估计法可获得比Candan估计器和apFFT/FFT相位差估计器更高的估计精度。本文对该估计器做两方面的改进：①拓展了原估计器的功能，从频率估计延伸到相位估计，实现了频率、相位联合估计；②引入频移补偿措施，使得无论信号频率怎样偏离，频率、相位都可以获得接近于克拉美-罗限的估计精度。经过以上两方面改进后的联合估计器，在无需增加样本的情况下，其频率估计方差仅为克拉美-罗限的1.33倍，而相位估计方差则完全达到克拉美-罗限。

1 基于前后向子分段和频移补偿的联合估计器

1.1 原有前后向子分段频率估计器的问题

文献[21]提出了前后向子分段频率估计器，其信号处理过程包括如下3个步骤：

步骤1将长度为2N-1的输入序列x(-N+1)～x(N-1)拆分为仅共同包含中心样点x(0)的前向和后向两个子分段，即{xf(n)=x(n),0≤n≤N-1}和{xb(n)=x(-n),0≤n≤N-1}；

步骤2分别对xf(n)、xb(n)做FFT，获得其峰值谱处的相位值φf(k*)、φb(N-k*)；

为说明该估计器工作原理，不妨令其输入x(n)为单频复指数信号序列，即

{x(n)=aexp[j(ω0n+θ0)],-N+1≤n≤N-1}

(1)

式中，频率ω0表示为如下形式

(2)

式中:Δω=2π/N;k*为FFT的峰值谱位置。

为估计频率ω0，将式(1)代入离散傅里叶变换的定义式，可推出这两分段的FFT谱Xf(k)和Xb(k)分别为

(3)

联立式(2)和式(3)，易证得Xf(k)和Xb(k)峰值谱分别位于k=k*处和k=N-k*处，从而有

(4)

故其峰值谱相位值为

(5)

将式(5)的两个相位项相减，可得频偏估计式

(6)

结合式(2)，则可推导出频率估计器表达式为

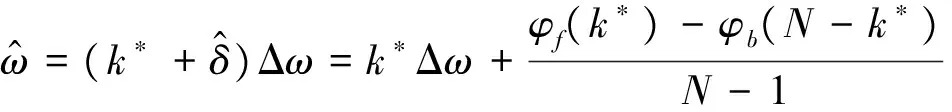
(7)

然而，文献[21]没有深入分析在噪声环境下影响估计器频率估计精度的内在因素。另外该估计器只完成频率估计，没有相位估计，故不是联合估计器。

1.2 估计器的改进思路

从式(5)不难看出，仅需对前、后向峰值谱相位值取平均，即可正负对消与频偏δ有关的两项，从而获得中心样点x(0)的瞬间相位，即

(8)

从而拓展了文献[21]估计器的相位估计功能。

对于单频复指数信号{x(n)=aexp[j(ω0n+θ0)]+w(n),-N+1≤n≤N-1}，其中w(n)为方差为σ2的零均值高斯白噪声，则信噪比ρ=σ2/a2。

文献[21]指出，前后向子分段频率估计器是无偏的，从而其估计方差与均方误差(Mean-Square-Error, MSE)相等。并且推导得出：前、后向谱峰相位值的理论方差相等，且当N足够大时, 为

(9)

从而对式(7)两边取方差，再与式(9)联立，有

(10)

类似地，由于式(5)中两个相位项的对消作用，式(8)的相位估计也是无偏的。由于两个子分段仅有1个样本x(0)重合，故两个峰值谱相位观测φf(k*)、φb(N-k*)近似相互独立，因而对式(8)两边取方差，有

(11)

1.3 引入频移补偿的联合估计器

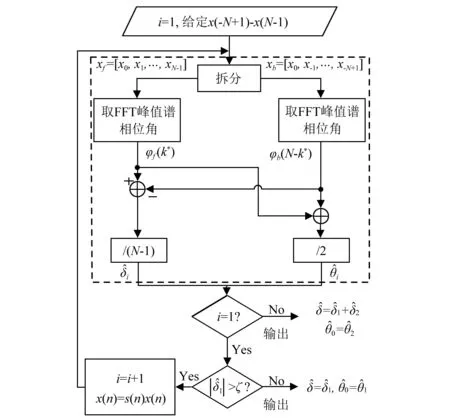
图1 基于频移补偿的改进的频率、相位联合估计流程Fig.1 Flow of modified frequency-phase joint estimator combining frequency shift and compensation

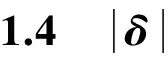
Rife等[9]指出，给定M个样本，对于信噪比为ρ的频率、幅值、相位均未知的复指数信号，其频率估计和相位估计的克拉美-罗限CRBω、CRBθ分别为

CRBω=6/[ρM(M2-1)]

(12)

CRBθ=2/(ρM)

(13)

然而，黄翔东等指出：Rife等导出的式(13)的相位估计克拉美-罗限是基于三参数模型的理论下限(在该模型中，要求利用频偏估计的结果来估计相位)。对于相位估计不依赖于频偏估计的估计器(如黄翔东等研究的apFFT相位估计器)，其相位估计符合的是仅涉及幅值和相位的两参数估计模型，其克拉美-罗限还要降低，仅为式(13)的1/4，即

CRBθ=1/(2ρM)

(14)

另外，由于式(2)的数学模型耗费了(2N-1)个样本，故将(2N-1)替代式(12)、式(14)中的M即可得本文提出的联合估计器的频率、相位值估计的理论下限，即

CRBω=3/[2ρN(N-1)(2N-1)]

(15)

CRBθ=1/[2ρ(2N-1)]

(16)

(17)

(18)

表1 基于频移补偿的改进的频率、相位联合估计步骤

2 仿真实验

令N=16，令频偏值δ在0.1～0.4变化，对{x(n)=exp[j(3+δ)2π/N(n+π/3)]+w(n)，-N+1≤n≤N-1}, 分别用原有的前后向子分段估计器和本文提出的引入频移补偿的前后向子分段联合估计器(阈值ζ设定为0.1)进行测频及测相，对于每种信噪比和频偏情况，做1 000 次Monte-Carlo模拟，并统计均方误差MSE。图2(a)～图2(d)给出了测频MSE曲线及其克拉美-罗限(另外还给出了Candan频率估计器、apFFT/FFT相位差估计器的MSE曲线作为对照)；图3(a)～图3(d)给出了测相MSE曲线及其克拉美-罗限(另外还给出了apFFT/FFT相位差估计器的MSE曲线作为对照，Candan估计器因未涉及相位估计，故无法做对照)。表2列出了SNR=20 dB时不同频偏情况下各方法的频率估计方差与式(15)的CRB比值，表3列出了不同频偏情况下SNR=20 dB时各方法的相位估计方差与式(16)的CRB比值。

从图2(a)～图2(d)、图3(a)～图3(d)及表2、表3，可总结如下规律：

(1)就频率测量而言，对于任意频偏情况，总体说来，本文提出的频移补偿+前后向子分段法的频率MSE曲线(‘□’标记)距离CRB最近，前后向子分段法(‘o’标记)次之，Candan内插法(‘▽’标记)距离CRB较远，apFFT/FFT相位差法(‘*’标记)距离CRB最远。在同样信噪比(SNR=20 dB)条件下，对于任意频偏，表2中的MSE值同样符合上述规律。因此，本文方法频率估计精度高于其他方法。

(2)就相位测量而言，对于任意频偏情况，总体说来，本文提出的频移补偿+前后向子分段法的相位MSE曲线(‘□’标记)距离CRB最近，前后向子分段法(‘o’标记)次之， apFFT/FFT相位差法(‘*’标记)距离CRB最远，该趋势同样反映在表3中。因此，本文方法相位估计精度高于其他方法。

(3)无论测频，还是测相，其他算法的估计精度都与频偏值δ有关：δ越小，均方误差越小，精度越高。即随着δ从0.1增加到0.4，前后向子分段法、Candan内插法与apFFT/FFT相位差法的MSE曲线都是偏离CRB越来越远，表2和表3给出的SNR=20 dB情况下的MSE值与CRB比值也越来越大；而本文提出的频移补偿+前后向子分段法则不然，无论频偏值为多大，其频率估计MSE曲线总是紧挨CRB(表2的测频方差与CRB比值约为4/3，验证了式(17)的正确性)，而相位估计MSE曲线则完全落在CRB曲线上(表3的测相方差与CRB比值近似等于1，验证了式(18)的正确性)。

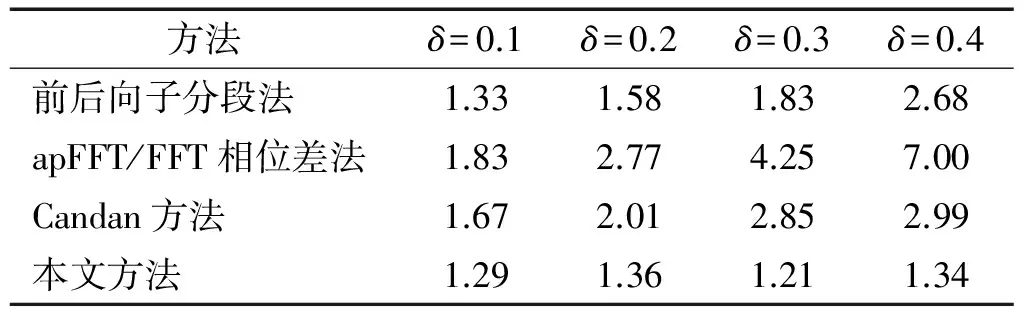
表2 测频方差与CRB比值(SNR=20 dB)

表3 测相方差与CRB比值(SNR=20 dB)

(4)需指出,在SNR较低的区域，所有频率估计方法都存在信噪比阈值SNRth，即当SNR

(5)需指出,在SNR较低的区域，三种相位估计方法也存在信噪比阈值SNRth。尤其从图3(c)～图3(d)可明显看出，当δ=0.3和δ=0.4时，apFFT/FFT法(‘*’标记)的SNRth比两种前后向子分段法都低。也就是说，apFFT/FFT法具有更高的抵抗大噪声干扰能力，这是因为黄翔东等指出：apFFT蕴含了全相位预处理过程，该过程可把噪声能量降低1/3，故抵御大噪声的鲁棒性更好，而本文方法不具备该特性，这也是高精度测相所付出的代价。

(a)δ=0.1 (b)δ=0.2 (c)δ=0.3 (d)δ=0.4图2 四种测频均方误差曲线及克拉美-罗下限曲线对照Fig.2 The comparison of the four frequency estimators’MSE curves and the Cramer-Rao lower Bound

(a)δ=0.1 (b)δ=0.2 (c)δ=0.3 (d)δ=0.4图3 三种测相均方误差曲线及克拉美-罗下限曲线对照Fig.3 The comparison of the three phase estimators’MSE curves and the Cramer-Rao lower Bound

3 结 论

本文提出引入频移补偿措施的前后向子分段频率、相位联合估计器，不但扩展了原有前后向子分段估计器不具备的相位测量功能，而且还借助频移补偿措施，提升了原有估计器的测量精度，其频率估计方差可达克拉美-罗限的1.33倍，其相位估计方差则完全达到克拉美-罗限。

需指出，本文得出的联合估计器的性能高于apFFT/FFT估计器的结论，是基于单频信号而言的。对于多频信号，存在谱间干扰问题，apFFT因其具有很好的抑制谱泄漏的性能，仍具有优势。提升本文估计器的多频信号测量精度是下一步要研究的工作。

[ 1 ] 青海银，张援农，周晨，等. 基于MST雷达垂直风速的大气温度剖面反演[J]. 物理学报, 2014, 63(9): 094301.

QING Haiyin, ZHANG Yuannong, ZHOU Chen, et al. Atmospheric temperature profiles estimated by the vertical wind speed observed by MST radar[J].Acta Physica Sinica, 2014, 63(9): 094301.

[ 2 ] ZHANG Y D, AMIN M G, HIMED B. Joint DOD/DOA estimation in MIMO radar exploiting time-frequency signal representations[J]. EURASIP Journal on Advances in Signal Processing, 2012(1): 1-10.

[ 3 ] 李传江，张自强，费敏锐，等.微速差双转子系统不平衡信号提取方法[J]. 振动与冲击, 2013, 32(14): 29-33.

LI Chuanjiang, ZHANG Ziqiang, FEI Minrui, et al. Extraction method for unbalanced signal in a dual-rotor system with little rotating speed difference[J]. Journal of Vibration and Shock, 2013, 32(14): 29-33.

[ 4 ] ZIBAR D, DE CARVALHO L H H, ESTARAN J, et al. Joint iterative carrier synchronization and signal detection employing expectation maximization[J]. Journal of Lightwave Technology, 2014, 32(8): 1608-1615.

[ 5 ] SINGH M, KHADKIKAR V, CHANDRA A, et al. Grid interconnection of renewable energy sources at the distribution level with power-quality improvement features[J]. IEEE Transactions on Power Delivery, 2011, 26(1): 307-315.

[ 6 ] WANG L, JIANG Q, HONG L, et al. A novel phase-locked loop based on frequency detector and initial phase angle detector[J]. IEEE Transactions on Power Electronics, 2013, 28(10): 4538-5349.

[ 7 ] 杨殿阁, 罗禹贡, 李兵, 等. 基于时域多普勒修正的运动声全息识别方法[J]. 物理学报, 2010, 59(7): 4738-4747.

YANG Diange, LUO Yugong, LI Bing, et al. Acoustic holography method for measuring moving sound source with correction for Doppler effect in time-domain [J]. Acta Physica Sinica, 2010, 59(7): 4738-4747.

[ 8 ] 梁美彦, 张存林. 相位补偿算法对提高太赫兹雷达距离像分辨率的研究[J]. 物理学报, 2014, 63(14): 148701-148705.

LIANG Meiyan, ZHANG Cunlin. Improvement in the range resolution of THz radar using phase compensation algorithm [J]. Acta Physica Sinica, 2014, 63(14): 148701-148705.

[ 9 ] RIFE D, BOORSTYN R. Single tone parameter estimation from discrete-time observations[J]. IEEE Transactions on Information Theory, 1974, 20(5): 591-598.

[10] CANDAN C. Analysis and further improvement of fine resolution frequency estimation method from three DFT Samples[J]. IEEE Signal Processing Letters, 2013, 20(9): 913-916.

[11] ABOUTANIOS E, MULGREW B. Iterative frequency estimation by interpolation on Fourier coefficients[J]. IEEE Transactions on Signal Processing, 2005, 53(4): 1237-1242.

[12] MACLEOD M D. Fast nearly ML estimation of the parameters of real or complex single tones or resolved multiple tones[J]. IEEE Transactions on Signal Processing, 1998, 46(1): 141-148.

[13] 王凤鹏，邹万芳，尹真，等. 希尔伯特变换实时全息干涉条纹相位提取 [J]. 光电工程, 2009, 36(4): 92-96.

WANG Fengpeng, ZOU Wanfang, YIN Zhen, et al. Phase extracting for real-time holographic interferometry fringe pattern based on hilbert transform [J]. Opto-Electronic Engineering, 2009, 36(4): 92-96.

[14] 沈廷鳌，涂亚庆，李明，等. 基于相关原理的相位差测量改进算法及应用 [J]. 振动与冲击, 2014, 33(21): 177-182.

SHEN Ting’ao, TU Yaqing, LI Ming, et al. An improved method for phase difference measurement based on correlation theory [J]. Journal of Vibration and Shock, 2014, 33(21): 177-182.

[15] 丁康, 钟舜聪. 通用的离散频谱相位差校正方法[J]. 电子学报, 2003, 31(1): 142-145.

DING Kang, ZHONG Shuncong. A universal phase diference correcting methods on discrete spectrum [J]. Acta Electronic Sinica, 2003, 31(1): 142-145.

[16] 毛育文, 涂亚庆, 肖玮,等. 离散密集频谱细化分析与校正方法研究进展[J]. 振动与冲击, 2012, 31(21): 112-119.

MAO Yuwen, TU Yaqing, XIAO Wei, et al.Advances and trends of study on discrete intensive frequency spectrum zooming analysis and correction methodology [J]. Journal of Vibration and Shock, 2012, 31(21): 112-119.

[17] 齐国清, 贾欣乐. 插值 FFT 估计正弦信号频率的精度分析[J]. 电子学报, 2004, 32(4): 625-629.

QI Guoqing, JIA Xinle. Accuracy analysis of frequency estimation of sinusoid based on interpolated FFT [J]. Acta Electronic Sinica, 2004, 32(4): 625-629.

[18] NOVOTNY M, SLEPICKA D, SEDLACEK M. Uncertainty analysis of the RMS value and phase in the frequency domain by noncoherent sampling[J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(3): 983-989.

[19] 黄翔东, 王兆华. 基于全相位频谱分析的相位差频谱校正法[J]. 电子与信息学报, 2008, 30(2): 293-297.

HUANG Xiangdong,WANG Zhaohua. Phase difference correcting sepctrum method based on all-phase spectrum analysis [J]. Journal of Electronics and Information Technology, 2008, 30(2): 293-297.

[20] 黄翔东, 王博, 杜宇彬, 等. 全相位 FFT 测相方差及其 Cramer-Rao 下限[J]. 数据采集与处理, 2013, 28(2): 161-165.

HUANG Xiangdong, WANG Bo, DU Yubin, et al. Variance of all-phase FFT measuring phases and its Cramer-Rao lower bound [J]. Journal of Acquisition and Processing, 2013, 28(2): 161-165.

[21] 黄翔东, 孟天伟, 丁道贤, 等. 前后向子分段相位差频率估计法[J]. 物理学报, 2014, 63(21): 204304.

HUANG Xiangdong, MENG Tianwei, DING Daoxian, et al. A novel phase difference frequency estimator based on forward and backward sub-segmenting [J]. Acta Physica Sinica, 2014, 63(21): 204304.

A forward and backward sub-segmenting frequency-phase joint estimator base on frequency shift compensation

HUANG Xiangdong, JIN Xukang, BAI Ruipeng

(School of Electrical and Information Engineering, Tianjin University, Tianjin 300072, China)

Frequency estimation and phase estimation are two basic measurement problems in physics. However, the existing estimators can hardly achieve high-accuracy joint estimation of these two parameters. To acquire the joint estimation, two aspects of improvement have been made on the original forward and backward sub-segmenting frequency estimator. On one hand, averaging the phase spectra of the peak fast fourier transform (FFT) bins of the forward sub-segment and the backward sub-segment yields an estimate of the middle sample’s instantaneous phase; on the other hand, frequency shift and compensation was introduced to concentrate the energy of the peak FFT bins of the aforementioned two sub-segments, which enhances the joint estimator’s resistance to noise and thus improves the accuracy. Both theoretical analysis and numerical simulation confirm that, the performance of the proposed joint estimator is superior to that of the original forward and backward sub-segmenting estimator and all-phase FFT/FFT phase difference estimator. For frequency offset cases, the frequency estimation variance of the proposed joint estimator is only 4/3 times of the Cramer-Rao lower Bound, and its phase estimation variance can reach the Cramer-Rao lower Bound.

joint estimator; frequency estimate; phase estimate; frequency shift and compensation

国家自然科学基金(61671012)

2016-03-30 修改稿收到日期： 2016-06-19

黄翔东 男，博士，副教授，1979年4月生

TN 911.72；TN98

A

10.13465/j.cnki.jvs.2017.16.032