杠杆平衡式起竖机构的建模与运动轨迹规划

刘毓希， 高钦和， 牛海龙， 程祥瑞

(火箭军工程大学 兵器发射理论与技术军队重点实验室， 西安 710025)

杠杆平衡式起竖机构的建模与运动轨迹规划

刘毓希， 高钦和， 牛海龙， 程祥瑞

(火箭军工程大学 兵器发射理论与技术军队重点实验室， 西安 710025)

针对特种车辆起竖过程中多级缸换级负载冲击大等问题，采用单级缸驱动的杠杆平衡式起竖机构，并建立了该机构的数学模型，推导出机构输入与输出之间的表达关系式；针对机构不同的运动情况对整体性能影响大的问题，提出采用正向规划和逆向求解规划的运动轨迹规划方法，并分析了这两种方法在不同场合下的适用情况。仿真与实验结果表明：该方法所建立的数学模型是正确的，且电动缸伸出长度与起竖角度有直接的数学关系；电动缸的运动速度与负载的起竖角速度有间接的比例关系，这说明在无传感器的情况下就可以监测负载的运动状况，为起竖机构运动规划时临界条件的判断以及今后的研究提供了重要的理论参考依据；正向轨迹规划有利于机构的快速起竖和减少最大输出功率，逆向轨迹规划有利于机构的平稳起竖。

杠杆平衡式起竖机构；数学建模；运动轨迹规划；无传感器测量

随着车载大型特种车辆多电化技术的不断发展与成熟，车载大型电驱动快速垂直起竖发射系统已成为了最近研究的热点[1]。传统的起竖机构一般采用直推式起竖，驱动缸行程长，起竖过程中冲击大，从而降低起升速度，影响导弹发射的生存能力[2-4]，因此本文提出了杠杆平衡式起竖机构，能够缩短电动缸行程，达到快速起竖的目的[5-6]。杠杆平衡式起竖机构结构较为复杂，一般都采用虚拟软件仿真分1析，缺乏数学理论推导计算，在对机构运动学特性进行深入研究时缺乏理论指导，分析不够透彻；此外，起竖机构的运动轨迹规划一般分为两种：正向规划和逆向规划，传统的起竖机构运动曲线规划一般采用逆解的方法，先已知负载的起竖角加速度，反推起竖力大小，其轨迹规划主要是考虑负载的最大速度、最大加速度以及最大冲击等因素[7-9]，着重倾向于运动过程中的平稳性，对起竖时间和功率没有优化，随着大型电动缸制造技术的不断发展和完善，大推力电动缸应运而生，起竖推力的大小已不再是限制起竖机构运动的瓶颈，因此，在满足负载可承受最大加速度的情况下，提高负载在初始阶段的加速度和末端的最大减速度能够实现导弹的快速垂直起竖。

针对上述背景，本文通过平面坐标系建立了杠杆平衡式机构的数学模型，为了解决中间过程计算量大的问题，首先通过Matlab进行数值仿真，然后采取多项式拟合的方法(Curve Fitting工具箱)对输入与输出的关系式进行数值拟合，从而减少了系统每次运行时繁琐的计算量，对机构的特性研究提供了很大方便。本文主要是建立电动缸的伸出长度与起竖角度的对应关系，然后通过数学运算推导出伸出速度与起竖角速度的对应关系，对于起竖机构的运动情况分析有很大的实际意义，即只需要知道电机的转速就能解算出起竖角速度，而无需传感器测量。

在起竖过程运动轨迹规划方面，本文根据以往的研究成果，分别从正向规划求解和逆向规划求解两方面对比仿真分析，得出了在机构运行过程中两种不同的方法产生的不同影响。经过实验验证，表明了数学推导和仿真的结果是正确的。

1 建立新型起竖机构数学模型

杠杆平衡式起竖机构较直推式起竖机构有电动缸行程短，在结构较为紧凑的同时还可以避免使用多级缸换级带来冲击等问题的影响，且较于其它形式的三角臂放大起竖机构，其举升支点靠近载荷的前部，起竖力小，构件受力状况得到改善。杠杆平衡式举升机构由电动缸O1A、三角臂O2AB和连杆BC组成，其举升运动初始位置和中间位置如图1所示。

图1 杠杆平衡式举升机构初始和中间位置示意图Fig.1 A schematic view of starting position and middle position on leveraged balance on lifting mechanism

电动缸伸出端作用于三角臂端点A，三角臂另一端点O2与车辆底盘铰接，剩余一端B通过连杆作用于负载底部C。举升过程中，电动缸推动三角臂O1绕转动，进而通过连杆推动负载绕O转动。部件间的约束关系如表1所示。

表1 杠杆平衡式起竖机构中各部件间的约束关系

以O点为坐标原点，建立如图1所示平面直角坐标系。用(x1,y1)表示I点坐标，LJK表示杆JK长度，FJK表示JK方向作用力，I、J、JK可取图中各点，G为负载重量，∠O1O2A=θ，∠COO3=ψ。设举升运动开始后经过时间t，O2AB转过角α至O2A′B′时，OC转过角β至OC′。其运动过程可以通过等式(1)进行描述

(1)

从式(1)可以计算出：消去xB′yB′xC′yC′这四个变量，即可得到角度α及B、C点坐标关于β的变化关系，而B、C点坐标为已知的初始条件。故

β=β(α)

(2)

电动缸伸出位移

(3)

电动缸伸出速度

(4)

电动缸伸出加速度

(5)

考虑到连杆、三角臂、电动缸等构件的质量与各铰接点摩擦力矩相对较小，故将其忽略。分别以负载和起竖臂为研究对象，由刚体的力矩平衡方程得

(6)

其中,

由式(6)可得举升力

(7)

联立式(1)～式(7)即可求得举升驱动力与举升运动规律的关系。举升力的大小主要受β、α两个变量的影响。

通过式(7)可以得出对于复杂的举升机构而言，求解起竖力大小是非常困难的，即使是通过计算机运算也需要花费大量的时间，这给后续机构的运动情况研究带来极大不利。因此，本文通过选择数值拟合方式简化计算。

结合式(2)、式(7)可以看出只要规划好α的变化规律就能求解出电动缸负载变化情况，由于α在负载起竖过程中不易测量，只能作为一个中间变量。又通过式(3)可建立α与电动缸伸出长度的变化关系，即

α=α(s)

(8)

结合式(2)式(8)可得s与β的关系

β=β(s)

(9)

综合上述可知，只需得到伸出速度v和起竖角速度ω即可求解出起竖机构的数学模型。

而电动缸的伸出速度与起竖角速度关系式又可以表示为

(10)

(11)

从式(10)和式(11)可以看出起竖角速度不仅与电动缸伸出速度有关，还与起竖角度关于伸出长度函数的导数大小有关。

同理

(12)

因此，在建立了电动缸的伸出速度与起竖角速度的关系式以后，只需知道其中的一个，便可求解出整个机构的数学模型，在数值分析部分将详细描述。

2 起竖机构的运动轨迹规划

机械系统在运动过程中必须要遵循的一个原则是运行过程时尽量平滑，避免位置、速度以及加速度发生突变，其中研究较为成熟的是机器人拾放操作和连续路径两种典型作业的轨迹规划，其轨迹规划方法有多种，包括摆线运动、分段函数、组合正弦、优化等速曲线以及多项式插值方法等规划曲线。规划曲线的由来在一些相关参考文献[10-12]中已有详细理论推导过程，同时在工程上得到了广泛应用。起竖系统在起升过程中与机器人的拾放操作有着类似的运动过程，因此在起竖机构轨迹规划中，根据起竖过程中的特性需求选取合适的规划曲线。

车载大型起竖系统在起竖过程中的运动轨迹规划[13]主要有两种思路：规划电动缸的伸出速度[14](正向规划起竖运动)，主要是遵循起竖过程中电机的功率变化趋势，起竖力大小的变化情况来规划曲线，以达到快速起竖为目的；规划起竖负载的角速度[15](逆向规划起竖运动)，主要是以负载平稳起竖为目的。

设轨迹规划函数为s(τ)，时间为t，起始时刻t=0，终止时刻t=T，则轨迹规划函数为s(τ)满足

(13)

2.1 电动缸伸出速度规划

大型导弹垂直起竖过程中，伺服电动缸在初始阶段起竖负载大，故电动缸的伸出速度不宜过大，以免造成大的冲击以及最大起竖力超出电动缸的承载范围；在起竖中间阶段，起竖力慢慢变小，为了达到快速起竖的目的，在功率允许范围内，电动缸速度快速提升，最后以匀速伸出；结束阶段，电机快速制动。(其速度变化曲线图如图4电动缸伸出速度(正)所示)，速度和位移规划曲线函数如式(14)式(15)所示

(14)

(15)

2.2 负载起竖角速度规划

紫阳道长几乎崩溃了，因为他完全没有想到内功修为称雄于世的天问大师竟然输得如此之惨，也在眨眼之间输掉了他们的自由！

该方法主要是在规划好起竖角速度的情况下，逆推电动缸的伸出速度，从而控制起竖运动过程。起竖角速度规划主要是考虑负载起竖过程中的平稳性，即导弹在运动过程中角加速度连续平稳变化，一般采用组合正弦曲线进行角速度规划(如图6起竖角速度(反)所示)，其满足的约束条件为

s(0)=0,s′(0)=0,s″(0)=0,

s(1)=1,s′(1)=0,s″(1)=0

起竖机构角速度和位移运动规划曲线如式(16)式(17)所示

(16)

(17)

3 数值分析

本文将主要通过正向规划求解和逆向规划求解作对比仿真实验，其基本原理框图如图2所示。

图2 两种方法的仿真原理框图Fig.2 The simulation block diagram of the two methods

在研究分析前需要确定的起竖机构的主要结构参数如表2所示，其中长度单位为mm；忽略起竖过程中的摩擦、风载荷等其他不确定因素的影响。设起竖终止角度为90°，整个起竖时间为40s，则反推过程中规划的组合正弦曲线的A2=90,k2=497.12。

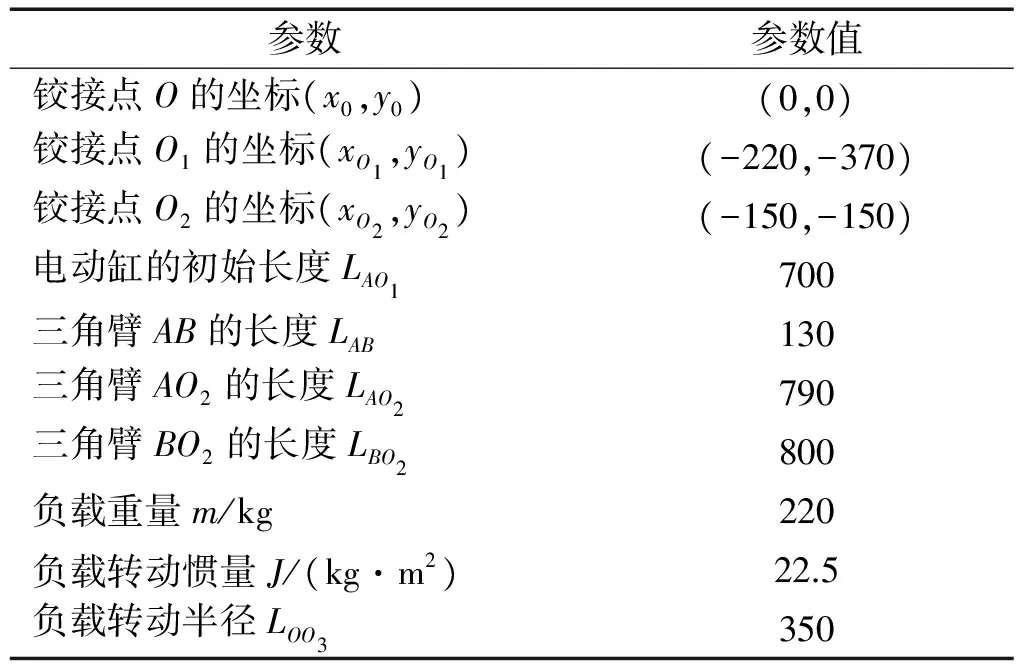
表2 起竖机构基本结构参数表

将反推规划曲线作为输入变量，通过积分求得起竖角度β，将其代入式(1)中求解出三角臂旋转角度α，将α代入式(3)中即可求的电动缸伸出位移s，从而找到电动缸长度与起竖角度的数值对应关系，得到如图3所示的曲线，利用Matlab/Curce Fitting工具箱对两者的数值关系拟合，得到其数学表达式如式(18)式(19)所示；正向规划求解过程与上述类似。

图3 电动缸的长度随角度的变化规律Fig.3 Variation of length on electric cylinders with angle

从图中可以看出电动缸的长度与起始角度是一一对应的关系(电动缸的初始长度为0.68 m)，利用Matlab中的Curve Fitting工具箱进行三次多项式拟合得出如下关系

s=-1.025×10-7β3+1.193×10-6β2+

0.004 055β+0.679 7

(18)

β=1 697s3-3 900s2+3 230s-926.8

(19)

对式(18)、式(19)分别进行求导

(20)

(21)

式中:s为电动缸总长度;β为起竖角度。

由式(18)可知当β=90°时，s=0.298 8 m,即A1=0.298 8 m，k1=2.774；

将式(14)、式(21)代入式(11)中，可以求解出起竖角速度的变化情况ω(t)，从而得到起竖过程中起竖力以及电动缸的功率变化情况，如图2所示,正向规划求解；将式(16)、式(20)代入式(12)中，即可求解出电动缸运行过程中的变化情况，直接对电机进行控制，如图2所示，逆向规划求解。

通过仿真对比分析：①从图4中得出，以起竖时间相等为约束条件，正推的最大伸出速度要小于反推的最大伸出速度(如果电动缸的最大运行速度一样，显然正推规划的方法可以节约时间，提高导弹的生存能力)；②从图4、图5中得出，在电动缸的伸出速度恒定时，起竖角速度继续增大，表明杠杆平衡式机构具有速度放大的特性；③从图6中得出，正向求解电机的最大输出功率要小于反向求解电机的最大输出功率。

图4 电动缸的伸出速度变化规律仿真对比图Fig．4Variationsimulationcomparisonchartofelectriccylinderextendingspeed图5 起竖角速度变化规律仿真对比图Fig．5Variationsimulationcomparisonchartoftheerectionangularvelocity图6 电机输出功率变化规律仿真对比图Fig．6Variationsimulationcomparisonchartofmotoroutputpower

综合上述可知,正向规划电动缸的伸出速度有利于机构快速垂直起竖：在相同的时间内，电动缸的最大运行速度较小，且最大角速度一样，最大消耗功率较小，如果保持两者最大运行速度，正向规划方法的起竖时间将会大大缩小。逆向规划起竖角速度的方法在导弹平稳性方面有优势：最大角加速度小，角速度变化平稳，适合大负载起竖系统。

4 实验验证

本文依托实验室电动缸调平起竖实验平台进行实验验证，如图7所示。实验平台的尺寸机构参数与仿真所用参数一致。实验平台中电气控制部分主要有工控机、控制卡、端子板、伺服驱动器、力传感器、倾角传感器、角度编码器等器件。其控制结构示意图如图8所示。

图7 起竖调平实验平台以及控制界面Fig.7 Erector leveling experimental platform and control interface

图8 电动缸平台整机电气控制结构图Fig.8 Electrical control structure on electric cylinder platform

为了验证起竖机构模型以及仿真结论的正确性，主要从两方面进行实验：电动缸伸出长度与起竖角度关系的实验验证；以两种规划思路分别对起竖机构的电动缸伸出速度以及起竖角速度进行规划，从而得出两种情况下的起竖角度变化情况以及起竖力的大小变化情况，与仿真实验做对比，验证仿真的正确性。在实验过程中，电动缸的速度作为输入，两种实验方法的原理框图如图9所示。

图9 两种方法的实验验证原理框图Fig.9 Block diagram of the experimental verification of the two methods

利用C#编写控制算法和界面进行人机交换实验，通过绝对编码器测量电动缸的伸出长度，通过相对编码器测量起竖角度变化大小。其实验结果与仿真结果对比如图10～图12所示。

通过上述实验与仿真对比可知，实验与仿真结果基本保持一致，证明了本文用数学公式推导所建立模型是正确的；从图10中可以看出电动缸的伸出长度与起竖角度是一一对应的数学关系与实验结果是相吻合的；由于结果一致，故中间过程利用的结论也应当是正确的，即已知伸出速度就可以求解出起竖角速度的结论也得到了验证。

5 结 论

本文主要针对车载大型起竖系统多级缸换级产生振荡冲击的问题以及多电化技术成为了自卸车发展潮流的背景下，采用了新型电驱动杠杆平衡式起竖机构。通过数学理论推导，找到电动缸伸出长度和起竖角度的关系表达式，通过多项式拟合的方法，大大简化了后续研究的繁杂计算量；以及推导出了伸出速度与起竖角速度的关系式，从而为起竖系统的输入与输出找到了连接关系，这说明在无传感器的情况下即可知道负载的运动状况，为起竖机构运动规划时临界条件的判断以及今后的研究提供了重要的理论参考依据。

图10 电动缸伸出长度与起竖角度的实验与仿真变化规律图Fig．10Experimentandsimulationvariationofextendedlengthanderectionangle图11 起竖角度随时间变化规律图Fig．11Experimentandsimulationvariationoferectionanglewithtime图12 起竖力大小实验与仿真情况变化规律Fig．12Experimentandsimulationvariationoferectingforce

通过两种运动轨迹规划仿真结果和实验的对比分析，验证了仿真结论的正确性，结果表明正向规划有利于机构的快速起竖，提高武器系统的生存能力，同时还能减小电机的最大输出功率；逆向规划求解有利于负载起竖过程中的平稳性，适合于大型负载的起竖。

[ 1 ] 夏倩倩.车载动能弹发射装置设计与动力学分析[D].南京：南京理工大学，2015.

[ 2 ] 李良，李锋，冯永保，等.基于自适应模糊滑模的大型液压起竖系统控制策略研究[J].兵工学报，2016，37(1)：71-76.

LI Liang，LI Feng，FENG Yongbao，et al. Research on control strategy of large hydraulic erecting system based on adaptive fuzzy sliding mode[J]. Acta Armamentarii，2016，37(1)：71-76.

[ 3 ] 谢政，谢建，杜文正，等. 大型发射装置液压起竖系统的滑模控制研究[J]. 兵工学报，2015，36(4)：674-680.

XIE Zheng，XIE Jian，DU Wenzheng，et al. Sliding mode control for hydrauli erecting system of large launcher [J]. Acta Armamentarii，2015，36(4)：674-680.

[ 4 ] 高钦和.大型装置起竖过程的电液比例控制研究[J].机械工程学报，2004,40(2)：190-192.

GAO Qinhe. Study on electro hydraulic proportion control in large sized mechanism erecting process[J].Chinese Journal of Mechanical Engineering，2004，40(2)：190-192.

[ 5 ] 刘敏杰，刘聚德. 几种举升机构的结构与性能分析[J].专用汽车，1999(2)：23-25.

LIU Minjie，LIU Jude. Structure and performance analysis of several lifting mechanisms[J]. Special Purpose Vehicle，1999(2)：23-25.

[ 6 ] 李明博，常晓权，刘君.导弹垂直起竖机构功率匹配性能研究[J].战术导弹技术，2012(2)：27-30.

LI Mingbo，CHANG Xiaoquan，LIU Jun. Research on power matching performance of missile vertical erecting mechanism[J]. Tactical Missile Technoligy，2012(2)：27-30.

[ 7 ] 田桂，谢建，陈永宁.大型导弹起竖过程最优时间轨迹规划研究[J].计算机仿真，2012,29(1)：41-44.

TIAN Gui，XIE Jian，CHEN Yongning. Time optimal trajectory planning for erecting process of large missile[J]. Computer Simulation, 2012，29(1)：41-44.

[ 8 ] 马长林，黄先祥，李锋，等.大型装置起竖系统智能积分控制仿真研究[J].兵工学报，2008，29(2)：227-231.

MA Changlin，HUANG Xianxiang，LI Feng，et al. Simulation study of intelligent integraion control for large mechanism erection system[J]. Acta Armamentarii，2008，29(2)：227-231.

[ 9 ] 丰佩.某车载垂直发射装置结构设计与动力学仿真分析[D].南京:南京理工大学，2015.

[10] ANGELDS J.机器人机械系统原理—理论、方法和算法[M].北京：机械工业出版社，2004：135-144.

[11] 宋伟刚. 机器人学[M].北京：科学出版社，2007：157-174.

[12] 田西勇.机器人轨迹规划方法研究[D].北京：北京邮电大学，2008.

[13] LEWIS R M, TORCZON V. A globally convergent augmented lagrangian pattern search algorithm for optimization with general constraints and simple bound[J]. SIAM Journal on Optimization，2002，12(4)：1075-1089.

[14] 吴向阳.车载大型导弹发射装置电驱动快速垂直起竖技术研究[D].北京：北京理工大学，2015.

[15] 冯江涛，郭晓松，姚晓光，等. 基于Simulink的起升系统联合仿真研究[J].机械科学与技术，2014，33(11)：1648-1651.

FENG Jiangtao，GUO Xiaosong，YAO Xiaoguang，et al. United simulation and research of lifting system based on simulink[J]. Mechanical Science and Technology for Aerospace Engineering，2014，33(11)：1648-1651.

Modeling and trajectory planning of leveraged balance on lifting mechanism

LIU Yuxi， GAO Qinhe， NIU Hailong， CHENG Xiangrui

(Military Key Laboratory for Armament Launch Theory & Technology，Rocket Forces Engineering University，Xi’an 710025， China)

The single-stage cylinder leveraged balance lifting solutions was proposed to solve multistage cylinder change-stage impact in lifting mechanism with building a mathematical model. Expression relationship of input and output was derived. For the question that different movement has a major impact on overall performance, application of different occasions is analyzed by adopting forward planning and reverse planning. The simulation and experimental results show that the developed mathematical model is corrected. Electric cylinder extending length has the relationship with erection angle directly. Movement speed of the electric cylinder and the erecting angular velocity of the load is indirectly linked. It shows that the movement of the load is known under no circumstances sensor which provides an important theoretical basis for analyzing Critical Condition in erecting mechanism motion planning and future research. Forward planning has an advantage on fast erection and reducing the maximum output power and reverse trajectory planning mechanism is in favor of a smooth erector.

leveraged balance on lifting mechanism; mathematical model; trajectory planning; none-sensor measurements

国家自然科学基金面上项目(51475462)

2016-05-16 修改稿收到日期： 2016-06-18

刘毓希 男，硕士,1991年生

高钦和 男，博士，教授，博士生导师，1968年生

TP273

A

10.13465/j.cnki.jvs.2017.16.033