多支承转子系统辛空间传递矩阵法及应用

张娟娟 ， 崔 升， 冯永新

(1. 复旦大学 航空航天系，上海 200433； 2.广东电网公司 电力科学研究院，广州 510600)

多支承转子系统辛空间传递矩阵法及应用

张娟娟1， 崔 升1， 冯永新2

(1. 复旦大学 航空航天系，上海 200433； 2.广东电网公司 电力科学研究院，广州 510600)

由变分原理出发，引入对偶变量，将多支承转子系统导入辛体系，推导出转子系统在辛空间中的传递辛矩阵格式,体现了保辛的性质。建立多支承转子系统模型，运用MATLAB对模型进行计算分析，求得固有频率等模态参数，计算结果与有限元方法计算值相吻合。通过与传统方法的计算结果比较证明了该计算方法的有效性。求解得到转子系统各阶临界转速，探讨了支承刚度的改变对转子各阶临界转速的影响，为多支承转子系统的优化设计提供了依据参考。

转子系统；辛空间；传递矩阵；应用

转子支承系统是旋转机械的主要部件，国内外许多学者已对其进行了大量研究[1-9]。传递矩阵法自50年代中期被应用于转子动力学分析，至今仍是转子动力学的主要数值分析方法之一[10]。袁惠群等[11]在Lagrange体系下运用传递矩阵方法对转子动力学特性进行了深入分析。在Lagrange体系下用传递矩阵法对转子系统进行动力学分析时，首先要对转子系统进行离散，简化为集总质量模型，把转子系统分为圆盘、无质量轴段和支承等单元，对各个单元进行受力分析，将各个单元两端状态向量之间的传递关系用传递矩阵来表示，根据连接条件求得转子系统的总传递矩阵，最后根据边界条件，求得涡动频率等模态参数。

对转子的动力学分析同样可以在辛体系下进行。钟万勰院士[12]将对偶变量体系引入到陀螺系统，从一个全新的角度研究了转子动力学问题，证明了辛空间中分析陀螺系统的优越性。隋永枫等[13-14]在辛空间中运用有限元等计算方法对转子进行了研究，更好地解决了一系列转子动力学问题。本论文将多支承转子系统导入辛体系，结合转子系统自身的特点，给出了在辛空间中的传递矩阵方法，体现了保辛的性质及计算方法的优越性，对运用传递矩阵法分析多支承转子动力学特性提供了一种新的思路。

1 理论基础

1.1 连续梁处传递矩阵的推导

本文转子系统模型的连接梁采用各向同性的铁木辛柯梁[15]，需要计入其转动惯量和剪切变形。

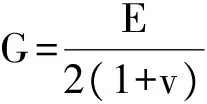
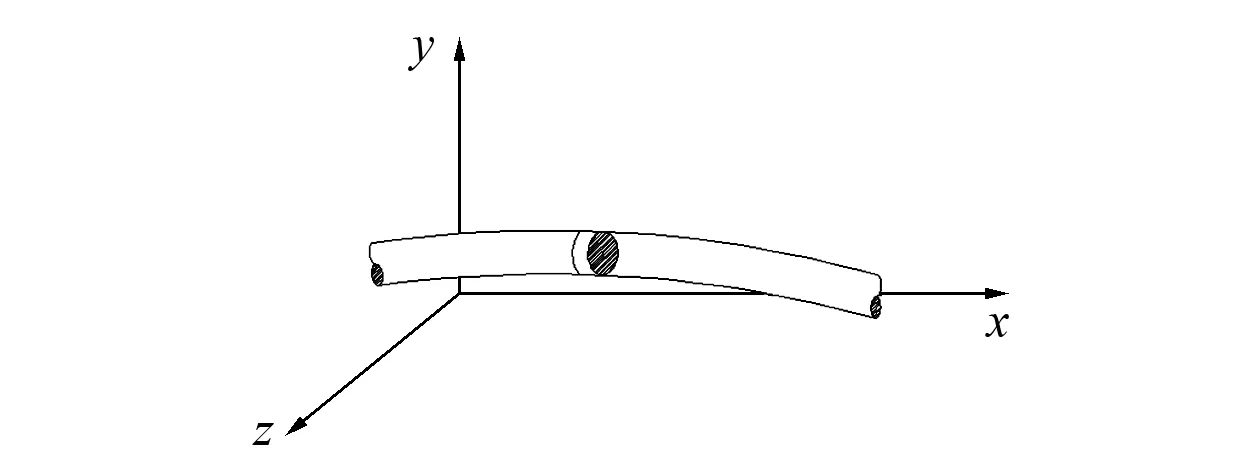
图1 单元梁示意图Fig.1 Beam element diagram

(1)

变形能表达式为

(2)

则拉格朗日密度函数为

(3)

(4)

引入复变量，设R=h1+ih2，则式(4)可以写为

(5)

在时域中采用Fourier展开法，即令R=q(x)e-iωt，可以得到

(6)

式(6)中空间部分的变分为

(7)

其中，

(8)

引入变量q的对偶变量

(9)

(10)

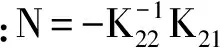
(11)

(12)

方程的解为

v=eHliv0

(13)

式中：li为此段梁的长度；v0和v分别为梁左端和右端的状态向量。其中，eHli为一个辛矩阵。

1.2 对支承及圆盘处连接条件的处理

对偶变量p的物理意义为

(14)

式中，Q跟M分别为梁的剪力和弯矩。因为所研究的是各向同性的转子系统，y方向与z方向具有相同的运动规律，所以取y方向进行分析可知，其全状态向量实质是v=[yθy-QyMy]。

将转子的弹性支承及圆盘看为一段梁左端的边界条件进行处理。取y方向进行分析，如果左端为弹簧，弹簧的刚度为ky，耦合刚度为kyz，对于各向同性转子系统，[yθy-QyMy]T=[Zθz-QzMz]T，则该段(第i段)左端的状态向量为

(15)

设单位矩阵为

(16)

单位辛矩阵为

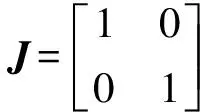
(17)

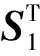
若左端为圆盘，圆盘的质量为m，则该段(第i段)左端的状态向量为

(18)

由辛矩阵的性质知，辛矩阵的乘积仍为辛矩阵 ，所以该算法是保辛的。

1.3 固有频率及临界转速的计算

设求得的总传递矩阵为

(19)

即

vR=TzvL

(20)

根据模型的边界条件，可得

即可计算出固有频率或临界转速。

2 模型的建立

各项同性转子简化模型如图2所示，该转子系统由一根转轴，三个支承，两个圆盘组成。转轴被支承及圆盘分为四段，每段的长度为2 m， 转轴的横截面为圆形，转轴的弹性模量为E=2×1011N/m，泊松比为0.3，密度为ρ=7 800 kg/m3，截面的惯性矩为J=4.952×10-4m4，三个支承处的等效支承刚度分别为k11=3.92×108N/m，k12=4.90×108N/m,k13=4.00×108N/m，两个圆盘的质量分别为m1=1.764×102kg,m2=2.067 8×

102kg, 转动惯量分别为jd1=10.78 kg·m2,jp1=20.58 kg·m2,jd2=29.498 kg·m2,jp2=58.212 kg·m2。

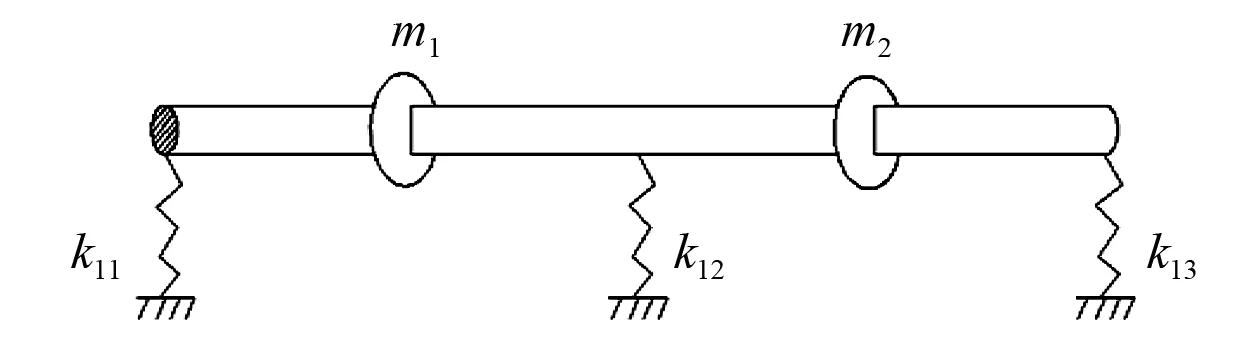
图2 转子模型图Fig.2 Rotor model diagram

3 转子系统计算分析

3.1 固有频率及振型的计算

在转子动力学分析中，有限元方法是一种有效的计算方法，发展已十分完善，在工程中有着十分广泛的应用[16-17]。本文运用MATLAB进行编程计算，以有限元方法的计算结果为基准，将本文计算结果与传统方法的计算结果进行比较。

由表1及图 3～图5 可知，本文方法计算的固有频率与有限元方法的计算结果非常接近，误差在可接受的范围内，具有较高的精确度，同时运用本文方法得到的振型曲线与有限元方法得到的振型曲线相吻合。与传统传递矩阵法相比，该方法在计算高阶涡动频率时避免了传统方法容易出现数值不稳定等缺点，体现出了本文计算方法的优越性，说明本文的方法是一种行之有效的计算方法。

表1 前四阶固有频率及相对误差

分别运用有限元方法及本文方法所求得的前三阶振型图如图3～图5。

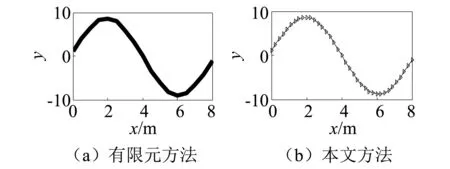
图3 一阶振型曲线Fig.3 First order mode curve

图4 二阶振型曲线Fig.4 Second order mode curve

图5 三阶振型曲线Fig.5 Third order mode curve

3.2 临界转速的计算

在实际工程中，通常只需考虑同向涡动时的临界转速。为了绘制坎贝尔图，需要求出多个自转频率所对应的各阶涡动频率。在本文中，自转角速度在0～1 000 rad/s内以50 rad/s为步长取了21个点，图6中的交点所对应的转速即为转子系统的临界转速。

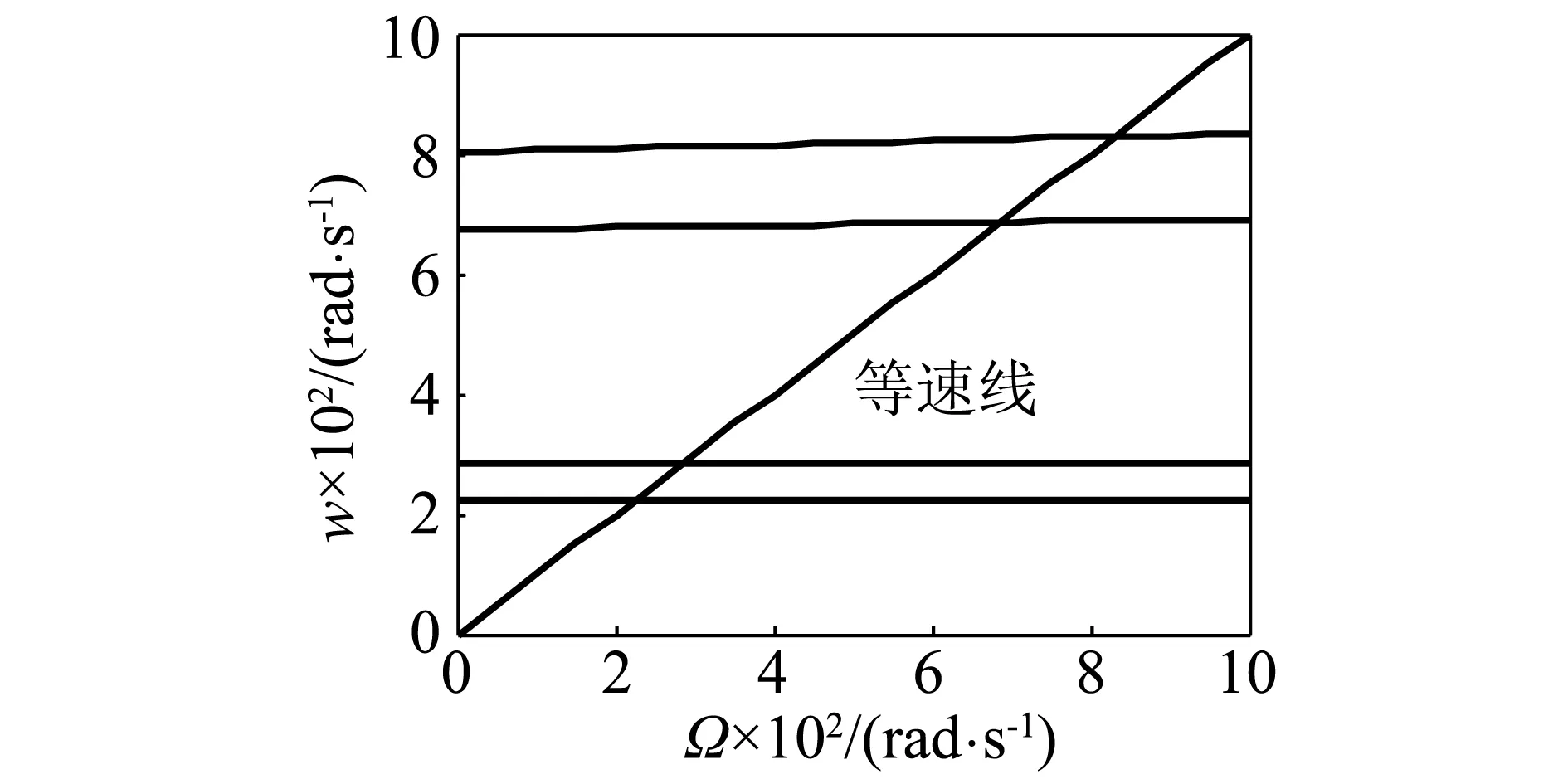
图6 坎贝尔图Fig.6 Campbell diagram

计算得到各阶涡动频率所对应的临界转速，如表2所示。

表2 各阶临界转速

表2的计算结果与图6相对应，也进一步说明了本文方法的有效性。由图6及表2可看出，在本文模型中，自转角速度的变化对涡动频率的影响不明显，第一阶临界转速和第二阶临界转速较为接近，第三阶临界转速和第四阶临界转速较为接近，实际工程中的转子在设计时，应当避免其工作时的转速在临界转速附近，以防止振动幅值过大。

3.3 频响分析

自转角速度在0～1 000 rad/s内以40 rad/s为步长点，算出了转子左端点在每个自转角速度下所对应的频响函数曲线，绘制出瀑布图，如图7所示。

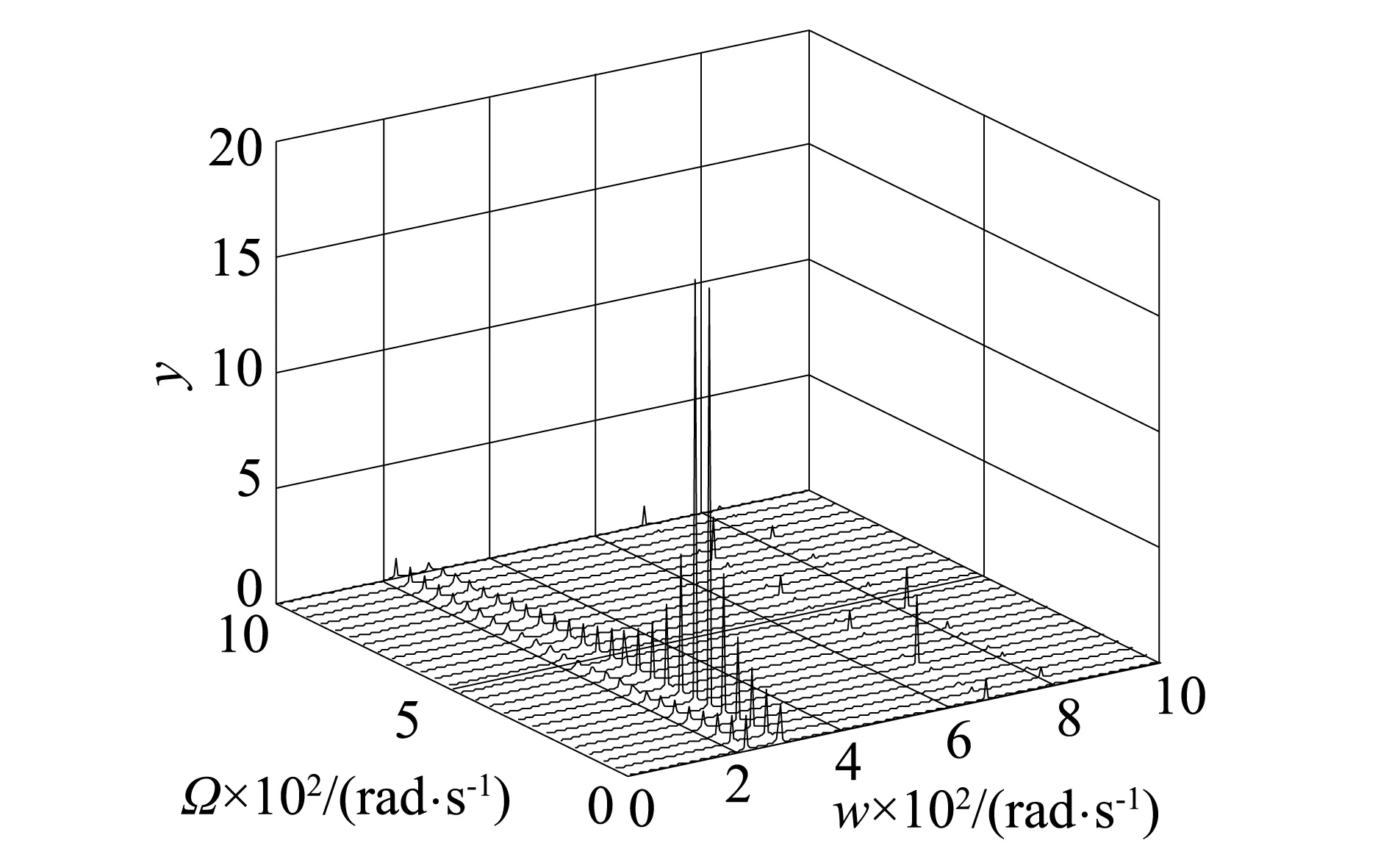
图7 瀑布图Fig.7 Waterfall plot

由图7可知，在本文模型中，转子的自转角速度对其涡动频率的影响不明显。图7所示的计算结果跟图6所示的计算结果相吻合，同时也验证了本文求解方法的有效性。

3.4 不同因素对临界转速的影响

在实际工程中，通常都是通过调节支承的刚度来对转子系统进行优化，本论文将讨论支承刚度的改变对多支承转子系统各阶临界转速的影响的几种情况。在讨论端部支承刚度的改变时，选取转子系统的左端为例进行讨论。在讨论同时改变两个支承刚度对各阶临界转速的影响时，通过比较发现同时改变中间跟端部支承刚度对临界转速的影响最大，故本文只给出了此种情况下的结果，同时改变两端支承刚度时可用类似方法进行分析。

(1)分别改变左端及中间弹性支承的刚度对各阶临界转速的影响。

由图8～图10可知，无论改变中间弹性支承还是端部弹性支承，随着支承刚度的增加，各阶临界转速都是先有一个快速上升的阶段，然后趋于平稳。支承刚度的改变对低阶临界转速的影响较小，对高阶临界转速影响较大。在本论文所讨论的转子系统中，通过对改变中间支承刚度跟端部支承刚度所得到的结果进行对比可知，中间支承刚度对各阶临界转速有较大的影响。

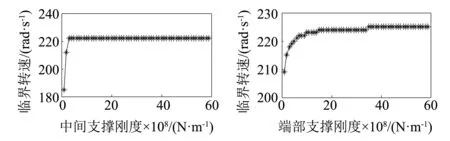
图8 对一阶临界转速的影响Fig.8 Influence on the first order critical speed

图9 对二阶临界转速的影响Fig.9 Influence on the second order critical speed

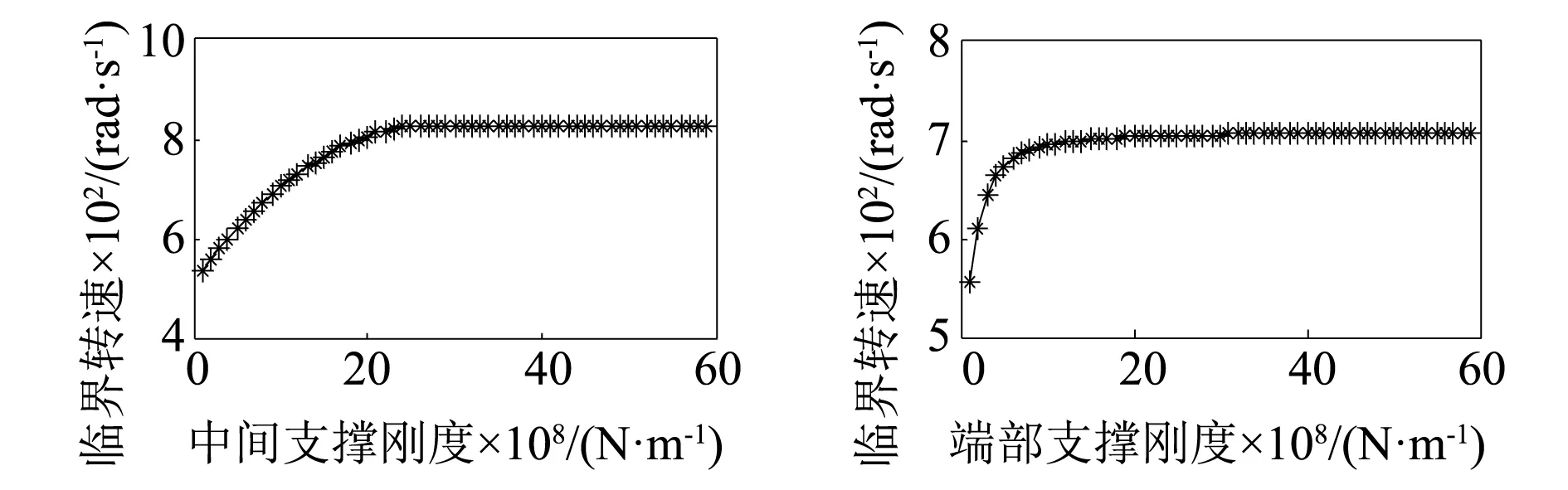
图10 对三阶临界转速的影响曲线Fig.10 Influence on the third order critical speed

(2)同时改变左端跟中间支承刚度对各阶临界转速的影响。

由图11～图13可知，随着两个支承刚度的增加，各阶临界转速都先有一个快速上升的阶段，然后趋于平稳。由图11～图13同样可以看出本文算例中，同端部支承相比，中间支承刚度对各阶临界转速的影响较大。

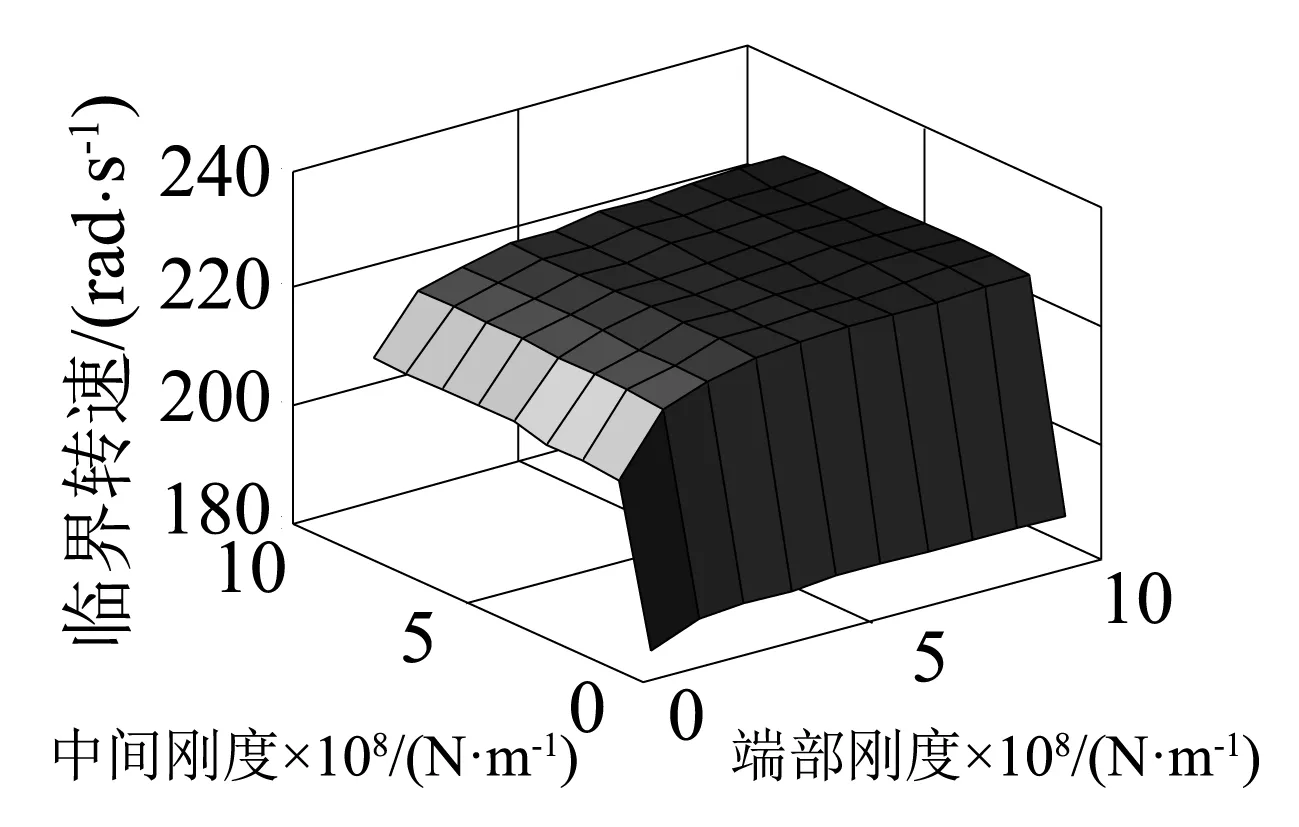
图11 对一阶临界转速的影响Fig.11 Influence on the first order critical speed

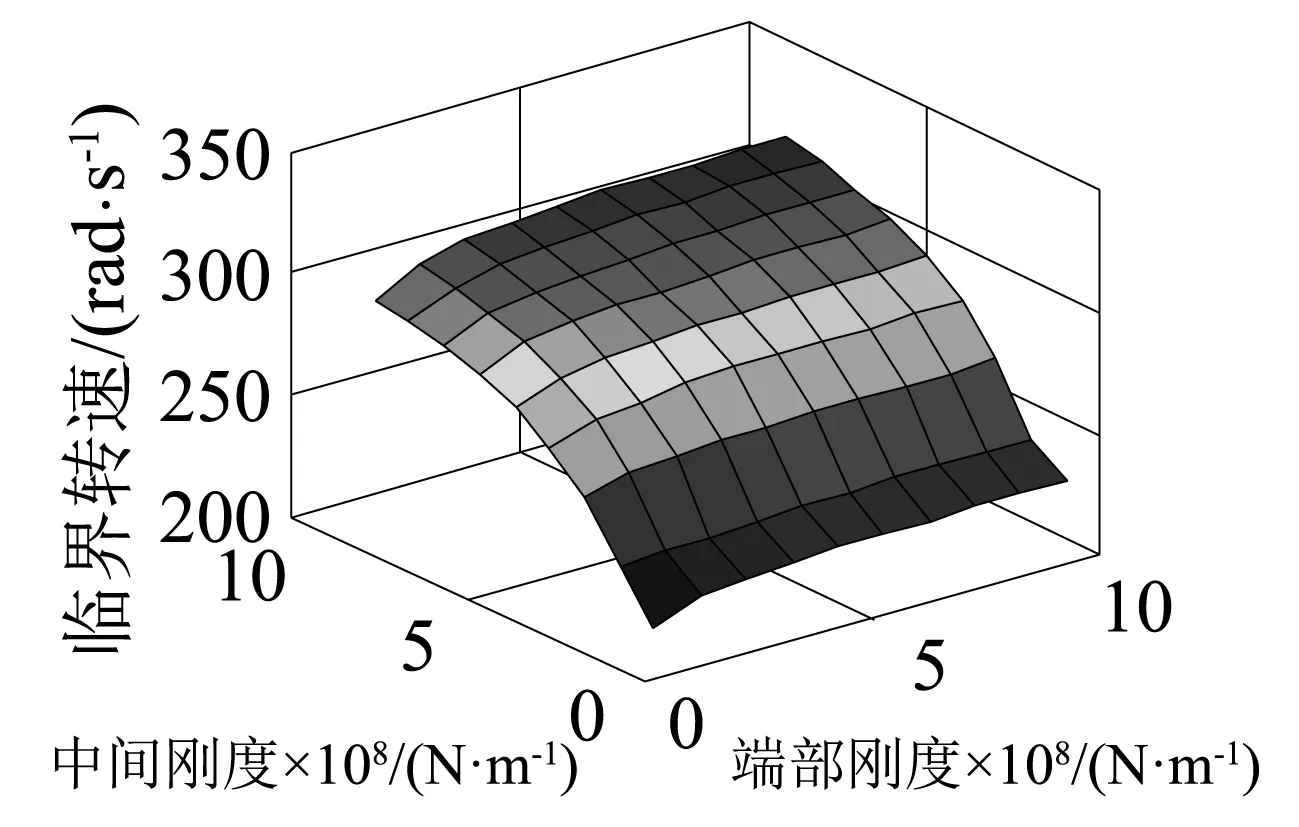
图12 对二阶临界转速的影响Fig.12 Influence on the second order critical speed

图13 对三阶临界转速的影响Fig.13 Influence on the third order critical speed

4 结 论

本文将多支承转子的动力学分析引入到辛体系中，运用辛方法推导出了状态向量之间的传递矩阵，该方法具有方便用MATLAB进行编程，计算速度快的优点。与传统的传递矩阵法相比较，该方法避免了求解梁的聚集模型等一系列复杂操作，便于理解，在计算高阶涡动频率时也可以得到比较精确的计算结果，体现出本文计算方法的有效性及优越性。同时本论文对临界转速及支承刚度的改变对临界转速的影响进行了分析，为转子系统的优化设计提供了依据。

[ 1 ] 孟光. 转子动力学研究的回顾与展望[J]. 振动工程学报, 2002, 15(1): 5-13. MENG Guang. Retrospect and prospect to the research on rotor dynamics[J]. Journal of Vibration Engineering, 2002, 15(1): 5-13.

[ 2 ] 杨永锋, 任兴民, 徐斌. 国外转子动力学研究综述[J]. 机械科学与技术, 2011, 30(10): 1775-1780. YANG Yongfeng, REN Xingmin, XU Bin. Review of international researches on rotor dynamics[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(10): 1775-1780.

[ 3 ] 徐小明, 钟万勰. 转子动力学的非线性数值求解[J]. 应用数学和力学, 2015,36(7): 677-685. XU Xiaoming, ZHONG Wanxie. Nonlinear numerical simulation of rotor dynamics[J]. Applied Mathematics and Mechanics, 2015,36(7): 677-685.

[ 4 ] 李强, 马龙, 许伟伟, 等. 椭圆轴承-转子耦合系统动力学特性研究[J]. 振动与冲击, 2016,35(11): 174-179. LI Qiang, MA Long, XU Weiwei, et al. Dynamic characteristics analysis of an elliptical bearing-rotor coupled system[J]. Journal of Vibration and Shock, 2016,35(11): 174-179.

[ 5 ] KIM J S, LEE S H. The stability of active balancing control using influence coefficients for a variable rotor system[J]. International Journal of Advanced Manufacturing Technology, 2003, 22(7/8): 562-567.

[ 6 ] 张文. 转子动力学理论基础[M]. 北京: 科学出版社, 1990.

[ 7 ] 何洪军, 荆建平. 非线性转子-密封系统动力学模型研究[J]. 振动与冲击, 2014, 33(10): 73-76. HE Hongjun, JING Jianping. Dynamic model of a nonlinear rotor-seal system[J]. Journal of Vibration and Shock, 2014, 33(10): 73-76.

[ 8 ] KIM T, NA S. New automatic ball balancer design to reduce transient-response in rotor system[J]. Mechanical Systems and Signal Processing, 2013, 37(1/2): 265-275.

[ 9 ] BEHZAD M, ALVANDI M, MBA D, et al. A finite element-based algorithm for rubbing induced vibration prediction in rotors[J]. Journal of Sound and Vibration, 2013, 332(21): 5523-5542.

[10] 钟一谔,何衍宗,王正,等. 转子动力学[M]. 北京: 清华大学出版社, 1987.

[11] 袁惠群. 复杂转子系统的矩阵分析方法[M]. 沈阳: 辽宁科学技术出版社, 2014.

[12] 钟万勰. 经典力学辛讲[M]. 大连: 大连理工大学出版社, 2013.

[13] 隋永枫. 转子动力学的求解辛体系及其数值计算方法[D]. 大连： 大连理工大学, 2006.

[14] 隋永枫, 高强, 钟万勰. 陀螺系统时间有限元方法[J]. 振动与冲击, 2012, 31(13): 95-98. SUI Yongfeng, GAO Qiang, ZHONG Wanxie. Time domain finite element method for gyroscopic systems[J]. Journal of Vibration and Shock, 2012, 31(13): 95-98.

[15] TIMOSHENKO S. 材料力学[M]. 北京: 科学出版社, 1978.

[16] 陈锡栋, 杨婕, 赵晓栋, 等. 有限元法的发展现状及应用[J]. 中国制造业信息化, 2010, 39(11): 6-8. CHEN Xidong, YANG Jie, ZHAO Xiaodong, et al. The status and development of finite element method[J]. Machine Design and Manufacturing Engineering, 2010, 39(11): 6-8.

[17] 孙海霞, 戴京涛, 姜伟, 等. 有限元法在机械工程中的应用与发展[J]. 科技创新导报, 2011(3): 84. SUN Haixia, DAI Jingtao, JIANG Wei, et al. Application and development of finite element method in mechanical engineering[J]. Science and Technology Innovation Herald, 2011(3): 84.

A transfer matrix method for a multi-support rotor systemin the symplectic space and its application

ZHANG Juanjuan1, CUI Sheng1, FENG Yongxin2

(1. Department of Aeronautics and Astronautics，Fudan University, Shanghai 200433, China; 2. Guangdong Power Test & Research Institute, Guangzhou 510600, China )

Based on the variational principle, dual variables were introduced, and the multi-support rotor system was imported into symplectic space. The symplectic transfer matrix in the symplectic space was presented for the rotor system, which reflects the symplectic conservation property. A model of the rotor system was built. MATLAB was used to analyze the model. The natural frequency and other modal parameters were obtained. The calculated values are consistent with the values obtained by the finite element method. The effectiveness of the method was confirmed by comparing the results with traditional methods. After large amount of calculations the critical speeds were obtained. The relationship between the critical speeds and the support stiffness was studied. This work provides reference for the optimization of rotor systems.

rotor system; symplectic space; transfer matrix; application

广东电网公司电力科学研究院科研基金

2016-10-12 修改稿收到日期： 2016-11-23

张娟娟 女，硕士，1990年1月生

崔升 男，博士，副教授，1967年9月生

O347.6

A

10.13465/j.cnki.jvs.2017.16.005