基于流形子带特征映射的转子复合故障特征提取方法

王广斌，李 龙，罗 军，杜晓阳，李学军

(1.湖南科技大学 机械设备健康维护湖南省重点实验室，湖南 湘潭 411201；2.中交第二航务工程局有限公司深圳分公司，广东 深圳 518067；3.中芯国际集成电路制造(深圳)有限公司，广东 深圳 518118)

基于流形子带特征映射的转子复合故障特征提取方法

王广斌1，李 龙1，罗 军2，杜晓阳3，李学军1

(1.湖南科技大学 机械设备健康维护湖南省重点实验室，湖南 湘潭 411201；2.中交第二航务工程局有限公司深圳分公司，广东 深圳 518067；3.中芯国际集成电路制造(深圳)有限公司，广东 深圳 518118)

针对复合故障特征易被噪声信号淹没，传统时频分析和流形学习方法不能完整有效的挖掘故障潜在信息和进一步实现故障特征提取。在流形学习的基础上提出了一种流形子带思想并将其应用到转子复合故障特征提取研究中，进而得出了一种基于流形子带特征映射的转子复合故障特征提取方法。对故障原始信号序列进行相空间重构，结合小波包对噪声的强烈抑制性和对信号分辨率高的特点，将重构信号分解成不同频带即子带。将同故障多种工况下的同一频带融合成频带矩阵并估计其本征维数，并通过拉普拉斯特征映射算法以本征维数为依据将子带降维获取低维特征向量并提取信息熵，进一步实现故障特征提取。实验表明，相对于经典的局部线性嵌入和拉普拉斯特征映射等算法，流形子带特征映射算法不仅对单故障而且对复合故障特征进行了更完整有效的挖掘和提取。

转子系统；流形子带；拉普拉斯特征映射算法；特征提取

以2000年在Science杂志上发表的两篇论文[1-2]为起点兴起的流形学习算法研究，使得机器学习、数据挖掘技术获得新动力。

经典流形学习算法有等距特征映射(Isometric Feature Mapping, ISOMAP)、局部线性嵌入(Local Linear Embedding, LLE)、拉普拉斯特征映射(Laplacian Eigenmap, LE)[3]、局部切空间排列(Locality Tangent Space Alignment, LTSA)[4]等。2012 年开始，逐渐有学者针对不同的问题，对时频分析和流形学习进行优势整合，提出不同类型的时频流形故障诊断方法。He等[5]研究了利用时频流形提取出机械健康诊断中的非平稳信号的本征特征，提出基于平Pseudo-Wigner-Ville分布、流形学习和相关匹配的时频流形方法，识别出轴承强背景噪声中的瞬态脉冲振动信号[6]，并总结出了利用时频流形方法进行特征提取和机械故障诊断的基本思路和方法流程[7]。Yi等[8]基于小波包变换和流形学习方法，通过提取来自二进制小波包变换的波形特征空间弱标签，检测滚动轴承微弱瞬态信号特征。Tang等[9]提出一种新颖的基于正交邻域保持嵌入算法和香农小波SVM的故障诊断方法。栗茂林等[10]提出连续小波系数非线性流形学习的故障特征提取方法，完整的获得了轴承的微弱冲击特征成分。李锋等[11]结合经验模态分解和自回归模型系数构造故障特性混合域特征集,利用LLTSA化简为故障区分度更好的低维特征矢量,并输入到最近邻分类器来识别轴承的故障模式。向丹等[12]提出一种基于经验模态分解(Empirical Mode Decomposition, EMD)、样本熵和流形学习的故障特征提取方法，成功的实现了变速箱滚动轴承故障分类评估。

在复合故障的诊断研究过程中，针对复合故障特征易被噪声信号淹没[13]，传统时频分析和流形学习方法不能完整有效的挖掘故障潜在信息和进一步实现故障特征提取。在流形学习的基础上提出了流形子带思想将其应用到转子复合故障诊断中。以转子系统正常、不平衡、松动[14]、不平衡-松动等4种状态信号为对象。首先对故障原始信号序列进行相空间重构[15-16]，结合小波包对噪声的强烈抑制性和对信号分辨率高的特点，将重构信号分解成不同频带即子带。然后将同故障多种工况下的同一频带融合成频带矩阵，并估计其本征维数。最后通过LE算法以本征维数为依据将流形子带降维获取低维特征向量并提取信息熵[17]，进一步实现故障特征提取。通过分析比较LLE方法、LE方法、证明流形子带特征映射方法不仅对单故障而且对复合故障特征进行了更完整有效的提取和挖掘。

1 流形子带

流形(Manifold)是一般几何对象的总称，是描述世界上各种物体存在的一种空间形式，包括一般的几何曲线、曲面和几何高维体，其数学理论基础是微分流形、黎曼几何、拓扑学和变分学，本质上是局部可坐标化的拓扑空间，可以看做是欧氏空间的非线性推广[18]。

子带指的是对数据进行多尺度分析时，不同尺度对应的时频域数据集。流形子带将子带概念从欧式空间拓展到流形上，从数据集的几何形态角度提出的，认为数据集是位于局部可坐标化的非线性流形上，在不同尺度分解得到的子带数据也具有全局流形结构，即每一个子带都位于局部子流形上，可以利用流形学习的算法进行子带的同胚映射，即每个子带数据都位于一个嵌入在高维空间的低维子流形上，以此作为流形假设，建立子流形上模式内在低维结构与观测变量间的非线性模型，获取数据的本质特征。

2 流形子带特征映射方法

小波包分析作为多尺度分析方法里面的一种，是在多分辨分析基础上构成的一种更精细的正交分解方法，能够为信号提供一种更加精细的分析与重构方法。它将频带进行多层次划分，不仅对低频部分进行分解，而且对高频部分也进行分解，并根据被分析信号的特征，自适应地选择频带，从而提高了时频分辨率，非常适合处理非线性和非平稳信号。LE算法能够很直观的降维目标，其原理是在高维数据的空间下相隔很近的点映射到低维空间下依然能保持彼此很近的距离，这对数据降维有非常积极的意义，然后通过Laplacian-Beltrami算子来构造对应的低维嵌入目标函数，以此实现高维数据最优低维嵌入的目标。因此采用这两种方法有机融合能很好的解决转子复合故障特征提取难的问题，其模型如图1所示。

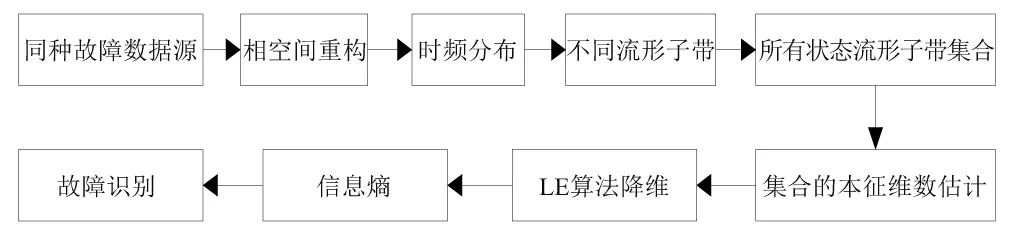
图1 流形子带特征映射方法模型Fig.1 Modelof rotor compound fault feature extraction

流形子带特征映射方法具体步骤如下：

步骤1 采集转子系统状态的振动时间信号序列

{x(ti),i=1,2,…,n}

(1)

步骤2 确定相空间重构中需要嵌入的饱和维数m和时间延迟参数τ可以将时间序列{x(ti),i=1,2,…,n}拓展m维的相空间中

Xi(t)=(x(ti),x(ti+τ),…,

x(ti+(m-1)τ)) (i=1,2,…,n)

(2)

步骤3 对重构的信号采用小波包分解即小波包分解选定小波函数之后，设定其滤波系数是τ={τn}， 令gk=(-1)kτ1-k。可以定义递归函数

(3)

(4)

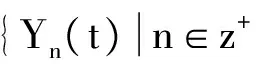
(5)

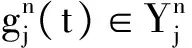
(6)

(7)

步骤4 将同故障多种工况下的同一频带融合成频带矩阵dN进行本征维数估计：取dN中一个中心点x，R(R足够小)为半径的球体Sx(R)内的密度f(x)≈a,a为常数，则得到非平稳过程{N(t,x),0≤t≤R}

(8)

可知N(t,x)是X1,…,Xn掉入球的样本点数Sx(t)，本文采用泊松过程来逼近，Tk(x)是X1,…,Xn中x的第k个近邻点到x的距离

(9)

式中，V(m)为m维单位球的体积，泊松过程参数是

λ(t)=f(x)V(m)mtm-1

(10)

式中，λ(t)为泊松过程的强度，定义θ=logf(x)，进一步对泊松过程建立其对数的似然函数

(11)

对式(11)采用极大似然方法，则有方程

N(R)-eθV(m)Rm=0

(12)

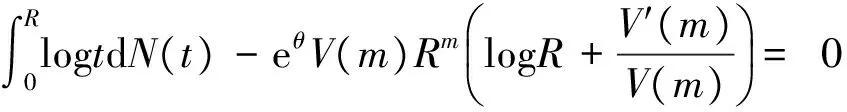
(13)

连解式(12)和式(13)可得

(14)

在实际的工程计算中，K-邻域比球面邻域更加方便，公式可以转化为

(15)

(16)

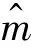
步骤5dN选取领域点，构造邻域图G

假设样本点xi与样本点xj之间的欧氏距离dij小于某一个既定的阈值ε，由此可以采用流形子带dN的样本点xi是样本点xj的近邻点，或者反过来样本点xj是样本点xi的近邻点。进一步则xi和xj在邻域图G中有边。

步骤6 赋权值w

方法1 若xi和xj相邻，设定wij=e-‖xi-xj‖2/t2；t表示常量，反之定义wij=0。

方法2 若xi和xj相邻，设定wij=1；反之定义wij=0。

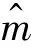
(17)

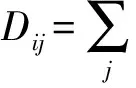
argmintr(YLYT)

(18)

可以看到：LE低维嵌入Y取的是拉普拉斯矩阵L里面最小的d+1个特征值所对应的特征向量v1,…,vd+1，即

Y=[v1,…,vd+1]T

(19)

步骤8 低维嵌入Y，提取信息熵

以低维嵌入Y分解为I层，在尺度i的清楚下，其多尺度分析的小波系数是Di(n)，在Di(n)上定义滑动窗口，定义短时窗长l，滑动步长是M，计算每一个信号多尺度分解成每一个尺度在某时窗内的信号能量

(20)

时窗内信号的能量之和等于每一个尺度分量的总和

(21)

而各个尺度信号的相对能量在时窗内是

(22)

(23)

步骤9 信息熵映射到二维空间，实现故障特征提取。

3 转子故障诊断实验

3.1 转子故障诊断实验系统

为验证流形子带特征映射算法的故障特征提取能力，采用美国Spectra Quest公司所提供的转子系统综合故障模拟试验台和丹麦的B&K的公司推出的PULSE数据采集系统(如图2所示)模拟和设计了转子系统复合故障实验。从两轴间轴承座上两侧采集的横向、径向和纵向3个方向一共6个传感器的振动信号数据，以此作为研究对象分析转子系统的正常、不平衡、松动、不平衡-松动4种状态。数据采集情况；对每一种故障在每一种转速(10 Hz、20 Hz、30 Hz、40 Hz、50 Hz)下采集1组信号，两端3个方向共6个传感器，一共120(5×4×6=120)组信号，采样频率是8 192，采集时间是10 s。

图2 转子故障模拟实验及数据采集Fig.2 Rotor fault simulation experiment and data collection

对采集的4种状态信号进行处理：采集到的原始数据构成了信息层，同时对原始数据进行消噪等预处理。然后对故障原始数据进行相空间重构，小波包分解成不同频带。再将同故障多种工况下的同一频带融合成频带矩阵并估计其本征维数。最后通过LE算法以本征维数为依据将流形子带降维获取低维特征向量，最后提取故障特征信息熵。数据处理流程如图3所示。

图3 数据处理流程图Fig.3 The flow chart of data processing

3.2 流形子带特征映射方法

将故障信号进行小波包分解，提取故障特征构成子带，从而提高了时频分辨率，也能有效的避免噪声的干扰。本文采用分别选取转子系统同状态在两端轴承座不同方位信号各4组一共24组采用‘db2’进行两层小波包分解，获得4个相对独立的频带，再将同状态多种工况下的同一频带融合成频带矩阵。通过LE算法进行降维处理，获得流形子带低维特征向量并提取信息熵。每个信号可以得到4个流形子带信息熵，将不同状态同一流形子带低维特征向量的信息熵进行分析类比。如表1所示。

表1 同一流形子带低维特征向量的信息熵

从表1可知，其中E=1×0-5，不同状态的低维特征向量得到的其信息熵，取值范围明显不同。其中四个流形子带中，流形子带1的信息熵值是最小的，基本上比其它子带的信息熵值小两个数量级；流形子带2中不平衡故障信息熵大多集中在0.002附近，松动种故障信息熵也都是比较聚集；流形子带3和流形子带4的信息熵是杂乱无章的。说明此方法对转子系统的故障的特征提取效果比较明显。进一步对每一种故障4组数据共16(4×4=16)组进行分析，采用二维直线型图展示其低维信息熵特征向量， 如图4所示。

图4 4种状态低维映射信息熵在同一流形子带分布Fig.4 Four state low-dimensional mapping information entropy in the same distribution manifold subband

图4中 ‘*’代表正常状态、‘+’代表不平衡故障、 ‘o’代表松动故障和‘x’代表不平衡-松动复合故障。由图分析对比：①转子4种状态在小波包分解之下得到的多组流形子带1集合经过拉普拉斯特征映射算法降维之后提取的信息熵值，同种故障之间的特征向量没有聚集比较分散而异类故障之间的特征向量值也没有彼此分开，4种故障状态的流形子带低维信息熵交织在一起无法分离；②图4(b)中可知正常状态和松动故障的信息熵值比较聚集；不平衡故障和复合故障这两种故障特征比较分散；异类故障特征之间都已分开，特征提取之后存在较大差异，4种状态的信息熵很明显分布在各个不同的Y坐标范围(即信息熵值区域范围)；③图4(c)4种状态后3组数据的信息熵彼此分开有一定的识别能力，第一组数据相近，在直线中存在交叉；④图4(d)虽然正常和松动两种状态特征存在一定程度上的聚集并彼此分开，但是没有和其他两种状态分开，类间信息熵距离也相对较小，故流形子带4对本文4种转子状态故障特征提取能力欠缺。

为验证文章方法的准确性而不是特例情况，以本文方法为依据，针对转子系统故障数据进行30次试验，分别的到图4(a)、图4(b)、图4(c)、图4(d)各30幅，结果表明流形子带1、3、4对于转子系统4种故障特征提取能力不足，而流形子带2的30次试验准确率达到96.7%，与前文结果表现一致，具体情况统计如表2所示。

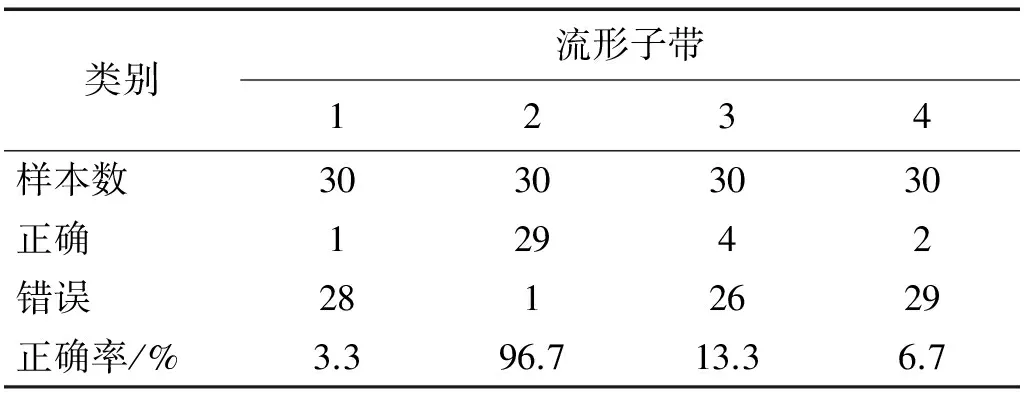
表2 4种流形子带低维信息熵试验正确率

3.3对比验证

采用经典的LLE、LE方法对本文4种转子状态进行特征提取，通过与流形子带特征映射方法进行分析比较，以常规流形学习方法提取故障特征如图5和图6分别是LLE和LE对转子4种状态源故障信号消噪的矩阵进行低维特征映射，获取其本质特征。

图5和图6中横、纵坐标分别表示为主特征分量1和主特征分量2，‘*’代表转子正常、‘+’代表不平衡故障、‘o’代表松动故障，‘★’代表不平衡-松动故障。可以看出传统经典的LLE方法对转子系统4种状态特征提取效果，在近邻点是k=8时4种状态交织在一起没有彼此分开，其它近邻点也无法提取故障特征。图6可知采用LE方法分析4种故障特征之间的特征聚集效果比较好，4种状态的类内距离比较接近，呈现出线状，正常和不平衡状态完全分开，特征提取效果良好。但松动状态和不平衡-松动故障之间存在着许多重叠部分，这两种状态特征提取效果欠佳。

为更加直观的与本文方法进行对比，以本文特征提取流程为基础，在LLE和LE方法低维特征映射后对特征量进一步进行信息熵特征提取，得到图7和图8的LLE和LE低维映射信息熵图。

图7中‘*’代表正常状态、‘+’代表不平衡故障、‘o’代表松动故障、‘★’代表不平衡-松动故障，观察可知4种故障特征的LLE算法低维映射信息熵在Y坐标范围分布凌乱，根本无法分离出异种故障特征；图8中正常和不平衡特征分开，效果良好。松动和不平衡-松动故障特征信息熵只有少许分离，存在很多交集，对这两种状态特征提取能力欠佳。

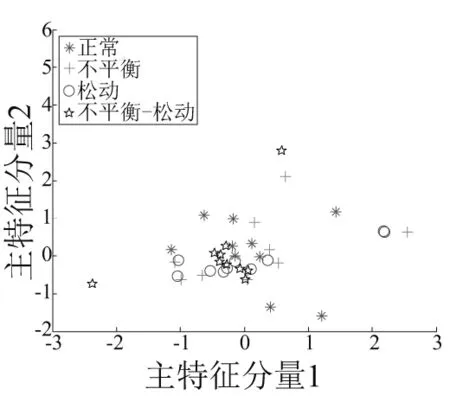
图5 LLE方法4种故障识别效果图Fig.5 Four kinds of fault identification effect of LLE method

图6 LE方法4种故障识别效果图Fig.6 Four kinds of fault identification effect of LLE method

图7 LLE方法低维映射信息熵图Fig.7 Low dimensional mapping information entropy diagram of LLE method

图8 LE方法低维映射信息熵图Fig.8 Low dimensional mapping information entropy diagram of LLE method

图9中，采用流形子带特征映射方法对4种故障进行识别。从中可以看出正常、不平衡、松动和不平衡-松动状态全部能够把故障特征分离，效果良好。同时流形子带特征映射方法也为转子系统复合故障特征提取提供了一种思路。

图9 流形子带特征映射方法的识别效果图Fig.9 Manifold subband feature mapping method to identify rendering

为了进一步证明流形子带特征映射方法对本文4种故障特征提取的有效性，以每一种故障10组数据为1个测试样本，共采用20个测试样本进行测试。如果以完全能识别4种故障为依据则LE故障识别率为0，显然不符合故障识别的要求。故将分别针对4种故障，采用20个测试样本同时进行，特征提取对比如表3。

表3 两种方法的特征提取效果对比

表3中LE低维映射信息熵和流形子带特征映射的故障识别率。针对20个测试样本，以每一种分离识别为依据，然后整合出算法对4种故障的识别率：LE对转子正常、转子不平衡的故障特征提取成功率分别是90%、90%，说明此方法对单故障的识别效果好；而转子基座松动以及不平衡-松动故障的成功率50%、15%，总的成功率因为复合故障降至61.25%。流形子带特征映射方法对4种故障的提取成功率分别是100%、95%、95%、90%，总的成功率是95%；证明了流形子带特征映射方法对转子系统不仅对单故障且对复合故障特征提取具有更明显的优势。

4 结 论

(1) 对实验所采集的转子系统的正常、不平衡、松动、不平衡-松动4种状态信号分别提取各频带的信息熵特征。结果表明，不同状态信号的低维特征信息熵特征值数值范围具有明显的区别。

(2) 提出了一种基于流形子带特征映射的故障特征提取方法。对故障原始信号序列进行相空间重构，将重构信号分解成不同频带即子带，然后将同故障多种工况下的同一子带融合成频带矩阵，最后采用LE方法将频带矩阵降维获取其低维映射，并进一步提取其信息熵。实现了故障本质特征深入挖掘和提取，同时避免噪声干扰，凸显出原始信号的各个频段的局部特性。

(3) 分析比较LLE、 LE，证明流形子带特征映射方法不仅仅对单故障而且 对复合故障特征提取具有更明显的优势，也为复合故障特征提取提供了一种方法和思路。

[ 1 ] SEUNG H S, DANIEL D L.The manifold ways of perception[J].Science, 2000,290(5500):2268-2269.

[ 2 ] ROWEIS S, SAUL L. Nonlinear dimensionality reduction by locally linear embedding[J]. Science,2000,290(5500):2323-2326.

[ 3 ] BELKIN M, NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation[J].Neural Computation, 2003,15(6):1373-1396.

[ 4 ] ZHANG Zhenyue, ZHA Hongyuan. Principal manifolds and nonlinear dimension reduction viatangent space alignmnet[J]. SIAM Journal on Scientific Computing,2005,26(1):313-338.

[ 5 ] HE Q B, LIU Y B, LONG Q.Time-frequency manifold as a signature for machine health diagnosis[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(5): 1218-1230.

[ 6 ] HE Qingbo, WANG Xiangxiang.Time-frequency manifold correlation matching for periodic fault identification in rotating machines[J]. Journal of Sound and Vibration, 2013, 332(10): 2611-2626.

[ 7 ] HE Qingbo. Time-frequency manifold for nonlinear feature extraction in machinery fault diagnosis[J]. Mechanical Systems and Signal Processing,2013,35(12): 200-218.

[ 8 ] WANG Yi, XU Guanghua, LIANG Lin, et al. Detection of weak transient signals based on wavelet packet transform and manifold learning for rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2015,54/55: 259-276.

[ 9 ] TANG Baoping, SONG Tao, LI Feng. Fault diagnosis for a wind turbine transmission system based on manifold learning and Shannon wavelet support vector machine[J]. Renewable Energy, 2014, 6(2):1-9.

[10] 栗茂林,梁霖,王孙安,等. 基于连续小波系数非线性流形学习的冲击特征提取方法[J]. 振动与冲击, 2012, 31(1): 106-112. LI Maolin, LIANG Lin, WANG Sun’an, et al. Mechanical impact feature extraction method based on nonlinear manifold learning of continuous wavelet coefficients[J].Journal of Vibration and Shock, 2012, 31(1): 106-112.

[11] 李锋, 汤宝平. 基于线性局部切空间排列维数化简的故障诊断[J]. 振动与冲击, 2012, 31(13): 36-41. LI Feng,TANG Baoping.Fault diagnosis model based on dimension reduction using linear local tagent space alignment[J].Journal of Vibration and Shock, 2012, 31(13): 36-41.

[12] 向丹, 葛爽. 基于EMD 样本熵-LLTSA 的故障特征提取方法[J]. 航空动力学报,2014, 29(7): 1535-1542. XIANG Dan,GE Shuang.Method of fault feature extraction based on EMD sample entropy and LLTSA[J].Journal of Aerospace Power, 2012, 29(7): 1535-1542.

[13] 刘韬, 陈进, 董广明. 基于频带熵的滚动轴承故障诊断研究[J]. 振动与冲击,2014, 33(1): 77-80. LIU Tao,CHEN Jin,DONG Guangming. Rolling element bearing fault diagnosis based on frequency band entropy[J].Journal of Vibration and Shock, 2014, 33(1): 77-80.

[14] 张靖, 闻邦椿. 两端支座松动转子系统的频率特性分析[J].中国机械工程,2008, 19(1): 68-71. ZHANG Jing, WEN Bangchun.A study of frequency characteristics of rotor sysrem with pedestal looseness at two supports[J]. Chaina Mechanical Eegineering,2008, 19(1): 68-71.

[15] PAEKARD N H, CRUTEHFIETED J P, FARMER J D,et al. Geometry from a time series[J]. Phys. Rev. Lett., 1980, 45(9): 712-716.

[16] TAKENS F. Determing strange attrae torsin tuthulenee[J]. Leeture Notes in Math, 1981, 898: 361-381.

[17] 周云龙, 张学清, 高云鹏. 基于小波包多尺度信息熵和HMM的气液两相流流型识别方法[J]. 核科学与工程,2009, 29(4): 333-339. ZHOU Yunlong,ZHANG Xueqing, GAO Yunpeng. A method for identifying gas-liquid two-phase flow patterns on the basis of wavelet packet multiscale information entropy and HMM[J]. Chinese Journal of Nuclear Science and Engineering, 2009, 29(4): 333-339.

[18] 陈维省.微分流形初步 [M].2版.北京:高等教育出版社,2001:2-5.

[19] 孙明明.流形学习理论与算法研究[D].南京：南京理工大学, 2007:5-12.

Rotor compound fault feature extraction based on a manifold sub-band feature mapping method

WANG Guangbin1， LI Long1， LUO Jun2， DU Xiaoyang3， LI Xuejun1

(1. Hunan Provincial Key Laboratory of Mechanical Equipment Health Maintenance, Hunan University of Science and Technology, Xiangtan 411201, China； 2. The Second Flight Engineering Bureau Shenzhen Branch, China Communications Construction Co., Ltd.,Shenzhen 518067, China； 3. SMIC IC Manufacturing (Shenzhen) Co., Ltd., Shenzhen 518118, China)

Compound fault features can be easily submerged by noise signals. Traditional time-frequency analysis and manifold learning methods cannot effectively mining the potential failure information for further fault feature extraction. The concept of manifold learning was proposed based on the manifold sub-band method and was applied to study compound rotor faults. Then a manifold subband feature mapping method was obtained. First of all, phase space reconstruction was performed for fault original signal sequence. Combining with wavelet packet strong inhibitory to noise and the characteristics of high resolution, reconstructing signal was decomposed into different frequency bands. The same frequency band of the same fault and many conditions were intergrated into the band matrix and estimated the intrinsic dimension. At last, low dimensional feature vector and subband dimension reduction were obtained by Laplace feature mapping algorithm based on the intrinsic dimension and the information entropy was extracted. Then the fault feature extraction was further realized. Experiments show that: compared with the classical local linear embedding and Laplace feature map algorithm, etc., the proposed method is not only effective for single fault but also for compound fault.

rotor system; manifold sub-band; Laplacian eigenmaps; feature extraction

国家自然科学基金项目(51575178；11572125)

2015-12-31 修改稿收到日期： 2016-06-29

王广斌 男，博士，副教授，1974年12月生

E-mail：jxxwgb@126.com

TP277

A

10.13465/j.cnki.jvs.2017.16.009