城市交通系统中宽扁梁结构的自由振动分析*

蒋吉清李钢魏纲魏新江孙泽星

城市交通系统中宽扁梁结构的自由振动分析*

蒋吉清1李钢2魏纲1魏新江1孙泽星1

（1.浙江大学城市学院工程分院，310015，杭州；2.铁道第三勘察设计院集团有限公司，300450，天津//第一作者，副教授）

为研究城市交通系统中宽扁梁的动力性能，由明德林（Mindlin）板理论退化得到板梁的控制方程，并推导出两端简支和两端固支板梁的自由振动特征方程，然后分别求解其自振频率和模态，并将计算结果与铁木辛科（Timoshenko）梁、Mindlin板的结果进行对比，总结板梁方程的梁宽适用范围并考虑泊松比对宽梁自由振动的影响。分析表明：相较Timoshenko梁方程，板梁方程更贴近Mindlin板的计算结果，尤其是前5阶自振频率，更适于较大泊松比的宽梁结构动力分析。

明德林板理论；板梁；铁木辛科梁；自振频率；振动模态

First-author′s addressSchool of Engineering，Zhejiang U－niversity City College，310015，Hangzhou，China

随着高架桥、地铁、轻轨等城市公共交通系统的快速发展，越来越多的宽梁结构被实际工程所采用，如多车道的桥面梁、中短型地铁浮置板道床等［1-3］。目前，就理论模型而言，学者们常采用Euler-Bernoulli梁理论或Rayleigh-Timoshenko理论模拟实际梁状结构［4-5］。前者也称为经典梁理论，适用于细长梁以及低中频振动问题的求解，如钢轨［6］、中长型浮置板等［7-9］；后者考虑了剪切变形和转动惯量的影响，适用于较大高跨比的深梁以及梁的高频振动问题和波动问题［10］。

然而，对于宽度较大的宽扁梁结构，现有的理论模型存在如下两方面问题：①若采用经典梁理论或Timoshenko梁理论，将无法考虑梁的宽度尺寸对计算结果的影响，而事实上梁的宽度越大，计算结果将越接近弹性力学板理论的结果；②若直接采用经典板理论或Mindlin板理论进行分析，虽能保障计算精度，但求解难度大幅增加，且在很多情况下都难以直接得到理论解，只能进行数值计算。

针对上述问题，本文将Mindlin板理论退化得到适用于宽梁结构的动力控制方程，称为Mindlin板梁方程（Mindlin plate-beam theory）。此外，推导得到不同边界条件下宽梁的自振频率和模态，并分别与Timoshenko梁理论和Mindlin板理论的计算结果进行对比。结果表明：对于宽梁结构，板梁理论的计算结果介于两者之间，比Timoshenko梁的结果更加精确，且在提高计算精度的同时保持了相对简洁的分析过程，具有良好的应用分析前景。

1 Mindlin板梁动力控制方程

1951年，在经典板理论的基础上，Mindlin考虑了转动惯量和剪切效应的影响，以此得到以下Mindlin板的控制方程［11］：

式中：

E——弹性模量；

G——剪切模量；

μ——泊松比；

ρ——材料密度；

k——剪切系数，k=π2/12；

h——板厚；

q——外荷载；

v——板厚方向的位移；

ψx，ψz——转角。

位移和转角的正方向如图1所示。假设ψx和v沿z方向保持不变，即ψx=ψx（x，t），v=v（x，t），并忽略式（1）中ψz的影响，经整理后，退化得到Mindlin板梁理论的基本方程［12］：

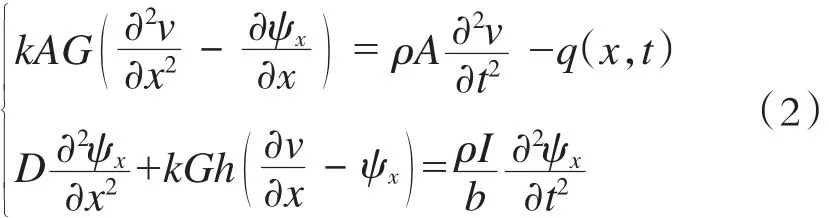
式中：

I——z轴的转动惯量；

b——截面宽度；

A——梁截面积。

由式（2）可发现，Mindlin板梁方程的形式与Timoshenko梁非常相似。事实上，式（2）即为从Mindlin板的角度得到的梁方程，该方程同时考虑了梁的宽度、剪切效应和转动惯量的影响。

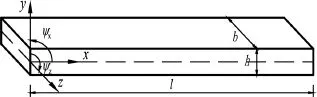
图1 板梁模型及坐标系示意图

2 Mindlin板梁自由振动分析

2.1 模态函数

对于某单跨均匀板梁，当不考虑外荷载作用时，Mindlin板梁（简称P-B板梁）的自由振动方程为：

式中：

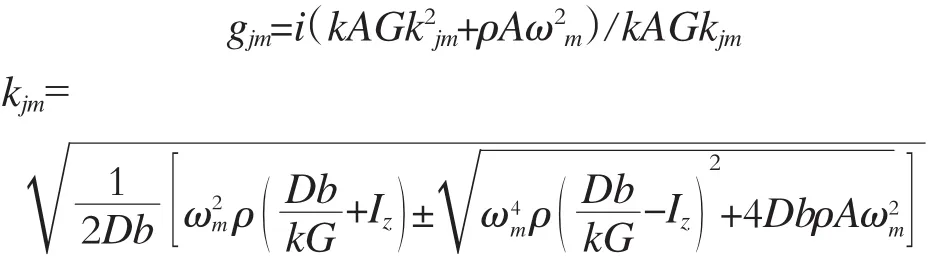
未知系数ajm和djm由板梁的边界条件确定（j= 1，2）。

由表1可知，路面经过冷补沥青修补料处治后，其抗滑性能可满足道路行车安全要求。该高速公路坑槽修补路面经过1年使用后，其表面骨料在行车荷载的作用下逐渐被磨光并趋向稳定，摩擦系数BPN均满足规范中对高速公路沥青路面摆值＞45的要求。

2.2 边界条件及特征方程

若板梁两端简支，则边界条件可表示为：

将v（x，t）位移和转角ψx（x，t）的表达式代入式（6），经整理后可得：

式中：

D（ω）——4阶方阵，其元素的具体表达式由边界条件（6）推导而得；

A——系数列向量，A=a1md1ma2md2m[

为得到系数矩阵A的非零解，必须满足

由此所得的方程即为频率特征方程，通过数值搜根可得到简支板梁的任意阶自振频率ωm。将ωm的值代回式（7），求解出系数矩阵A，并将其归一化，分别代入式（4）和式（5），即可求得模态函数Um（x）和ψm（x）。

当板梁两端固定时，只需将边界条件改为：

按照同样的步骤可得到D（ω）的表达式及其行列式方程。对于其它复杂边界条件（如弹簧支座等），以上方程也同样适用。

3 数值算例及分析

为分析P-B板梁的动力性能，本文采用跨高比l/h=20的宽梁模型（相当于中长型浮置板的跨高比），并将计算结果与Timoshenko梁（简称T-B梁）理论及Mindlin板（简称M-P板）理论的结果进行对比，其中M-P板的自振频率采用SAP2000软件进行计算。最后，根据数值结果讨论P-B梁方程的梁宽适用范围以及泊松比取值的影响。

为消除具体参数数值的影响，采用无量纲分析，其中无量纲自振频率系数ωi的表达式为［13］：

式中：

ωi——第i阶自振频率。

3.1 板梁方程的梁宽适用范围

如前所述，P-B梁方程适用于宽梁结构的动力分析。此处将采用不同的宽度条件，并将P-B梁的计算结果分别与T-B梁和M-P板的自振频率进行比较，以得到板梁方程的梁宽适用范围。

3种不同理论的前10阶无量纲频率系数如表1所示。在两端简支的边界条件下，P-B梁的自振频率与M-P板（对边简支、对边自由）的结果更为接近，尤其是工程中常用的前5阶频率。当b/h从1逐渐变化到10（典型单向浮置板）的过程中，M-P板与P-B梁的第5阶频率误差仅为0.93%；同阶的T-B梁误差为3.02%，是P-B梁的3.2倍，可见板梁理论跟Mindlin板理论的计算结果更吻合。

随着梁宽增加，P-B梁与M-P板的自振频率吻合阶数逐步降低（表1中虚线所示部分）。当b/h= 4时，两者的前8阶频率吻合较好；当b/h=6时，前6阶吻合较好；而当b/h=10时，仅前5阶符合较好。需指出的是，P-B梁理论和T-B梁理论都属于一维线弹性理论，因此，梁的宽度大小并不直接影响计算结果，只有M-P板的自振频率会随着宽度的变化而变化。此处讨论不同的宽度取值只是为了探讨P-B梁理论的适用范围。

简支条件下P-B梁的各阶模态函数也可相应求得，部分结果如图2所示。

图2 简支板梁的自振模态

表1 单跨简支宽梁的自由振动频率系数（μ=0.3）

考虑其它边界条件（如两端固定），所得的3类理论模型的自振频率变化趋势与简支情况类似，具体如表2所示。根据前述计算结果，可简要总结如下：在b/h≤4的范围内，应用P-B梁理论计算宽梁的动力特性能够获得良好的结果。

3.2 泊松比的影响

对于宽梁而言，横向变形效应即泊松比的影响较为显著。如表3所示，随着泊松比的增大，T-B梁自振频率有微小下降，在对边简支、对边自由的边界条件下，当μ=0.1和0.5时，第1阶、第4阶和第8阶自振频率的变化分别只有0.005%、0.070%和1.950%。但相同条件下，P-B梁的自振频率随泊松比的增大而显著增大，相应阶次的自振频率的变化分别为7.070%、5.600%和2.790%。

表2 两端固定宽梁的自由振动频率系数（μ=0.3）

P-B梁与T-B梁的同阶频率差异也随着泊松比的增大而增大，具体如图3所示。此外，通过与M-P板进行对比发现，当b/h≤4时，P-B梁的计算结果无论从数值上还是趋势上，都更接近M-P板理论，但随着板宽的进一步增大（当b/h=5），两者的差异增大，再次验证了第3.1节关于板梁的梁宽适用范围的结论。

4 结论

图3 不同泊松比下两端简支梁的频率系数

表3 泊松比对两端简支T-B梁和P-B梁频率系数的影响

根据Mindlin板理论退化得到适用于宽梁结构的板梁控制方程，推导板梁的自由振动特征方程，求解出不同边界条件下的自振频率和模态函数。与Timoshenko梁理论、Mindlin板理论的自振频率进行对比，总结出板梁方程的梁宽适用范围，并分析了泊松比对自由振动特性的影响。

具体算例表明，无论采用两端简支或两端固支的边界条件，当宽厚比b/h≤10时，板梁方程和Mindlin板方程的前5阶自振频率非常吻合，且宽厚比越小，频率吻合的总阶次越高。同时，随着泊松比的增加，板梁理论的计算结果相比较Timoshenko梁理论精度更高。

综合而言，Mindlin板梁方程适用于宽度效应显著（b/h≤4）、泊松比μ较大的宽扁梁结构分析，如中短型浮置板等，所得结果与二维Mindlin板理论的结果十分贴近，但可避免Mindlin板复杂的求解过程，具有良好的应用前景。

［1］孙晓静，刘维宁，张宝才.浮置板轨道结构在城市轨道交通减振降噪上的应用［J］.中国安全科学学报，2005，15（8）：65-69.

［2］蒋崇达，雷晓燕.钢弹簧浮置板轨道结构谐响应分析［J］.城市轨道交通研究，2013，16（11）：25-31.

［3］李再帏，练松良，刘晓舟.浮置板轨道对地铁车辆振动影响的实测分析［J］.城市轨道交通研究，2013，16（9）：23-26.

［4］TIMOSHENKO S P.Vibration Problems in Engineering［M］. New York：Wiley，1974.

［5］TIMOSHENKOS P.On the correction forshearofthe differential equation for transverse vibrations of prismatic bars［J］. Philosophical Magazine：Series 6，1921，41（245）：744-746.

［6］张建鹏.钢轨的振动及其模态分析［J］.城市轨道交通研究，2013，16（4）：74-76.

［7］HUSSEIN M F M，HUNT H E M.Modelling of floating-slab tracks with continuous slabs under oscillating moving loads［J］.Journal of Sound and Vibration，2006，297（1）：37-54.

［8］HUSSEIN M F M，HUNT H E M.Modelling of floating-slab track with discontinuous slab part 1：response to oscillating moving loads［J］.Journalof Low Frequency Noise，Vibration and Active Control，2006，25（1）：23-39.

［9］KUO C M，HUANG C H，CHEN Y Y.Vibration characteristics of floating slab track［J］.Journalof Sound and Vibration，2008，317（3）：1017-1034.

［10］徐志胜，翟婉明，王开云.基于Timoshenko梁模型的车辆-轨道耦合振动分析［J］.西南交通大学学报，2003，38（1）：22-27.

［11］MINDLIN R D.Influence of rotatory inertia and shear on flexuralmotions of isotropic，elastic plates［J］.Journalof Applied Mechanics，1951，18（1）：31-38.

［12］MINDLIN R D.Thickness-shear and flexural vibrations of crystalplates［J］.Journal of Applied Physics，1951，22（3）：316-323.

［13］CALIM F F，AKKURT F G.Static and free vibration analysis of straight and circular beams on elastic foundation［J］. Mechanics Research Communications，2011，38（2）：89-94.

Analysis of Plate-beam Free Vibration in Urban Traffic System

JIANG Jiqing，LIGang，WEIGang，WEIXinjiang，SUN Zexing

To study the dynamic analysis of plate-beam，the governing equations are derived from the Mindlin plate theory，the characteristic equations of simply-supported ends and clamped-clamped beam ends are obtained respectively.Then，the natural frequency and normal mode are calculated and compared with those of the Timoshenko beam and Mindlin plate，a suitable range of length-to-width ratio is concluded for the application of the plate-beam theory and the influence of Poisson's ratio on the free vibration of wide beam.As the result，the plate-beam theory is proved to have better agreement with the Mindlin plate theory rather than the Timoshenko beam equations，especially for the first five frequencies.

Mindlin plate theory；plate-beam；Timoshenko beam；natural frequency；vibration mode

TU311.3；U448.21+2

10.16037/j.1007-869x.2017.08.004

2017-01-22）

*浙江省自然科学基金项目（LY17E080005）；国家自然科学基金项目（51278463，51508506）