考虑加劲肋的悬挂式单轨轨道梁挠度研究*

谢倩王月明蒋咏志谭鸿愿

考虑加劲肋的悬挂式单轨轨道梁挠度研究*

谢倩王月明蒋咏志谭鸿愿

（西南交通大学机车车辆工程系，610031，成都//第一作者，硕士研究生）

为研究悬挂式单轨轨道梁的加劲肋对其整体挠度的影响，建立了静活载作用下超静定变截面梁的力学模型，以模拟其变刚度条件下的弯曲变形，并推导出轨道梁任意截面的转角和弯曲挠度变形的一般方程。应用Matlab软件编程实现了梁最大挠度的计算机求解，并根据求解结果对悬挂式单轨轨道梁进行了初步的结构优化设计探讨。

悬挂式单轨交通；轨道梁；加劲肋；挠度

Author′s addressInstitute of Rail Vehicles，Southwest Jiaotong University，610031，Chengdu，China

悬挂式单轨交通作为一种快捷舒适、安全节能、造价低、富有观光趣味的城市轨道交通方式逐渐吸引了人们的关注。目前，德国、日本、东南亚等国的一些城市已开始采用这种交通工具作为城市骨干交通或者短途客运专线交通。在中国一些城市，如温州等地也正在筹备建设悬挂式单轨交通［1］。

悬挂式单轨交通的轨道为一条由墩柱支撑的带型梁体，车辆悬挂于轨道下行驶。轨道梁不仅是承重结构，也是列车运行的轨道，还是供电、通信等缆线的载体。轨道梁由外壳、走行轨、导向轨、导电轨4部分构成，以钢板焊接而成开口薄壁箱型截面梁结构［2］。车辆运行时，通过走行轮在走行面上滚动而行驶在轨道梁下方，并通过导向轮矫正行驶方向。因此，轨道梁下端对称凸缘结构将承受最大外载荷，即车厢的自重和载重。为增强轨道梁的刚度，一些悬挂式单轨的轨道连续梁采用了加劲肋结构。目前，应用于悬挂式单轨轨道梁的加劲肋主要存在两种形式：一种是在轨道梁外部以一定间隔离散地加外层环筋，有些单轨的外层环筋为厚度不可忽略的钢条，如多特蒙德大学校园的单轨轨道梁（见图1），环筋为横隔板与纵向加劲肋的组合模式，有些单轨的外层如日本千叶的单轨轨道梁（见图2）［4］；另一种是在梁体的内部加以连续纵向肋板，如日本湘南的单轨轨道梁［5］。

图1 多特蒙德大学的单轨轨道梁

加劲肋设置过多不仅增加自重和变形，而且降低经济性；加劲肋数量过少，能减少用钢量但也会导致梁体弯曲变形增大，势必为减小挠度而增加梁的截面刚度来保证行车安全。轨道梁的成本通常远高于车辆成本，所以，单轨轨道梁的设计非常重要，在允许的挠度范围内优化轨道梁的结构与加劲肋间距，具有十分重要的意义。

图2 日本千叶的单轨轨道梁

1 轨道梁力学模型

文献［6］通过精确有限无法对施加跨中载荷的日本千叶县悬挂式单轨轨道梁进行了应力分析和挠度计算，其中为考虑加劲肋的作用，将走行面假设成用横向加劲肋弹性支撑的多跨连续梁。针对加劲肋导致的梁体纵向不连续性，本文将轨道梁假设为变截面（变刚度）梁来计算挠度。

假设：单跨跨长为L，加劲肋纵向宽度为m；间距为l；两端夹持处为加劲肋端；其中无加劲肋部分惯性矩为Iw，加劲肋部分惯性矩为Ij。将轨道梁截面简化为开口薄壁箱型，选取其中主要特征量作为设计参数（见图3、图4）。

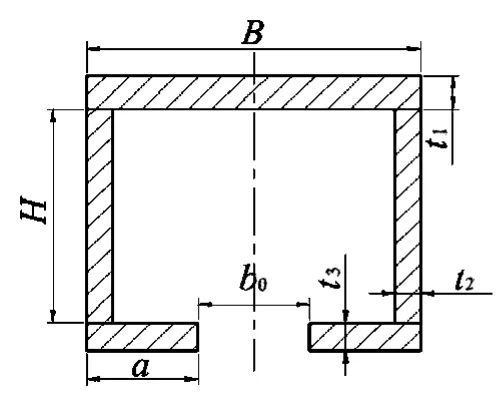
图3 无加劲肋轨道梁截面

图4 加劲肋轨道梁截面

因开口箱型断面梁对称，弯心C位于y轴上，与上盖板的间距用z0表示，则可计算两种截面下的弯心轴惯性矩如下：

由于梁跨之间采用铆钉竖向排布固定，因此假定轨道梁两端为固定支座。建立两端作用有反力偶矩的超静定梁力学模型和x-y直角坐标，坐标原点为梁左端支座（见图5）。假设梁的抗弯刚度沿x方向分成n段变刚度段，则L=m+（n-1）（m+l）/ 2，其中第k段等刚度段的抗弯刚度为EIk，两端变刚度截面坐标为xk-1和xk。

图5 超静定轨道梁力学模型

设计列车置于直线轨道梁内，导向轮与梁体侧壁之间没有预紧力，所以忽略列车在直线轨道梁段行驶时梁体所承受的横向作用力等，并假设直线轨道梁仅承受竖向作用力，由钢结构自重+列车活载荷+列车竖向冲击力组成。梁质量所产生的自重载荷假设为轨道梁相同截面段内所受均布力q=ρA（N/m），其中密度ρ取16 Mnq钢的密度7 850 kg/m3，梁截面面积A根据有无加劲肋分为Aj和Aw，则两种截面下的均布力为：

列车活载荷取列车满员时的载荷（轴重P= 32.81 kN）。假设某时刻列车相对于单跨轨道梁处于其正中位置，则集中载荷F按式（5）计算。

式中：

F——轨道梁走行轮轨接触区域集中力，N；

P——车辆轴重，kN；

将单跨轨道梁的载荷简化为在最中间的等刚度段内承受一个轮压集中力。假设最中间段为第c段，c=（n+1）/2，段内有单个集中力F，其作用位置坐标为xcp=L/2；轨道梁两端支座处转角变形和挠度变形为0，梁端作用的支反力为R0、R1，反力偶为M0、M1。

2 轨道梁变形方程

定义广义阶梯函数：H（x）=（x-a）n，n≥0。当x≤a时，H（x）=0；当x＞a时，H（x）=（x-a）n。以下各式中都使用此函数。将超静定梁第k段沿截面截断，选取左段为研究对象。规定力向上为正，力偶顺时钟为正，则根据力偶平衡关系，得梁第n段任一x截面的弯矩方程为［8-9］：

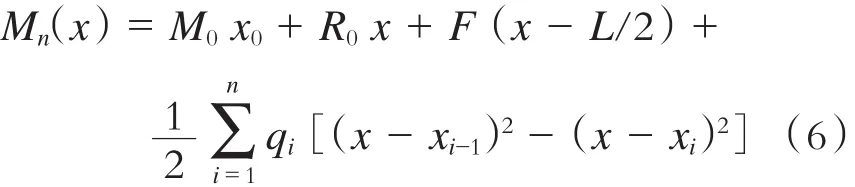
在小变形情况下，梁弯曲变形服从虎克定理，其变分和平衡方程不仅对等刚度梁成立，对变刚度梁也同样成立［10-11］，故第n段内x截面的转角变形θn（x）和挠度变形yn（x）满足如下微分方程：

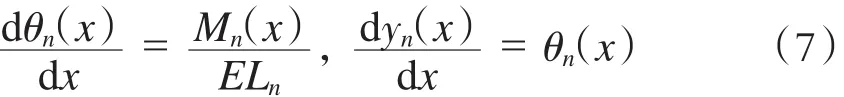
在第n段内的区间（xn-1，x）上，对式（7）中转角变形微分方程积分得：

θn（x）-θn（xn-1）=［Fn，1（x）-Fn，1（xn-1）］/（EIn）（8）式中：

应用式（9）将静不定梁第1段到第n-1段各段端转角方程排列并相加，由于x0=0和θ1（x0）=θ0，并定义变刚度梁抗弯刚度函数1/（EDi）=1/（EIi）-1/（EIi+1），化简得：

得到：

应用式（11）和式（12）将静不定梁第1段到第n-1段各段两端挠度方程排列并相加简化，由于对称性，可得如下变刚度静不定梁的挠度变形方程：

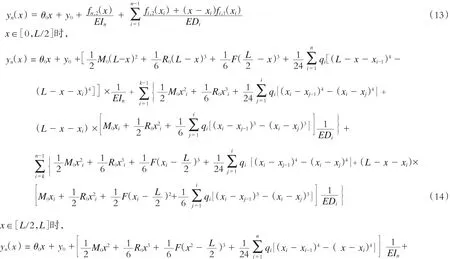
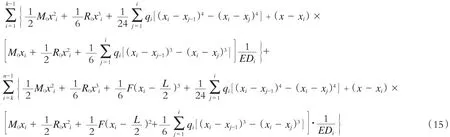
通过Matlab软件编程求解后，得到轨道梁的弯曲竖向变形随轨道梁横坐标x的变化趋势如图6所示。

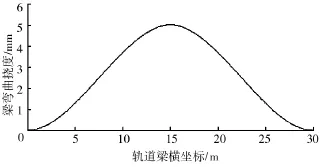
图6 直线轨道梁竖向弯曲挠度

3 轨道梁挠度影响因素及结构半人工优化设计

以加劲肋间距l、纵向宽度m及梁各部分板厚t作为挠度的影响因素来进行分析。算例借鉴国内关于日本轨道梁结构的设计研究［2，5-6］，取轨道梁L= 30 m，a=300 mm，B=1 060 mm，H=760 mm，其他拟定变量初选取的范围如表1所示。

表1 各变量取值范围

为保证列车平稳安全地在轨道梁上运行，轨道梁须满足刚度条件，根据《城市轨道交通设计规范》［7］和德国相关标准［12］，轨道梁许用挠度为：

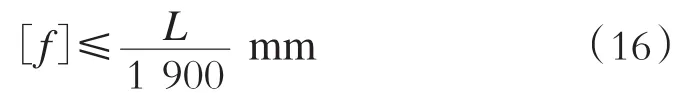
箱型轨道梁的走行轨所在翼缘的局部翻转失稳也是校核重点。根据焊接梁受压翼的局部稳定性校核方法［13］，规定焊接梁受压翼缘的外伸宽度不大于（t为翼缘板厚，mm；σS为钢材的屈服强度，N/mm2，16 Mnq钢的屈服强度为345 MPa）。将列车走行轨所在的下支撑板视为受压翼缘，其设计宽度不超过300 mm。取本文算例翼缘的最小板厚10 mm进行验算，得：

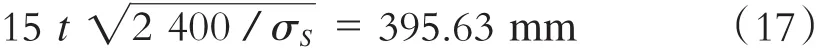
上述计算结果大于翼缘设计宽度300 mm，即梁体板厚增大到15 mm也可有效保证轨道梁的翼缘局部稳定性。因此，仅讨论加劲肋的设计参数对轨道梁的竖向挠度即结构刚度的影响。

3.1 加劲肋间距

设单轨轨道梁跨距、加劲肋纵向宽度及梁各部分板厚固定，许用挠度［f］=15.79 mm，加劲肋间距变化时的计算结果如表2所示。其中：加劲肋宽度m取平均值0.15 m；梁顶板、翼缘、走行面板板厚t1、t2、t3及加劲肋板厚t5均取最小值10 mm，以便对比出不同加劲肋间距时最大挠度的变化；加劲肋槽宽t4则取平均值0.15 m。整段轨道梁用钢量其中n为变刚度总段数。

表2 跨度30 m直线梁不同加劲肋间距计算结果

加劲肋间距l从约0.5 m增大至近1.6 m时，30 m跨度下轨道梁的竖向最大变形量由于平均惯性矩的减小而导致强度减小，因此，近似呈抛物线性增大趋势，而用钢量则近似呈双曲线性减小趋势（见图7）。故该跨度下，所选取的任何加劲肋间距均能满足许用挠度条件。

图7 不同加劲肋间距下直线梁的竖向最大挠度

3.2 加劲肋宽度

设单轨轨道梁跨度、加劲肋间距及梁各部分板厚固定，加劲肋宽度变化时梁挠度计算的结果如图8所示。其中：加劲肋间距（参考l/m极限比例）取0.6、1.0、1.4、1.6 m共4组值［4-6，12］；梁顶板、翼缘、走行面板板厚t1、t2、t3及加劲肋板厚t5均取最小值10 mm，以便更大程度地对比出不同加劲肋间距时最大挠度的明显变化，另外加劲肋槽宽t4则取平均值0.15 m。

图8不同加劲肋宽度下梁的竖向最大挠度

图8 显示了在不同加劲肋间距（0.6 m、1.0 m、1.4 m、1.6 m）下，当加劲肋宽度在0.1～0.2 m范围内逐渐增大时，由于自重增加和相对强度增大对挠度影响程度较大，30 m跨度下轨道梁的竖向最大变形量随之近似呈线性增大趋势，同时也随着加劲肋间距的增大而增大；在不同加劲肋间距（0.6、1.0，1.4、1.6 m）下，当加劲肋宽度在0.1～0.2 m范围内逐渐增大时，用钢量随之减小，而最大变形量随着加劲肋间距的增大而逐渐增大，与图9趋势相符。同样，在该跨度下所选取的任何加劲肋间距均能满足许用挠度条件。

由于随加劲肋间距增大，轨道梁的竖向最大变形量近似呈抛物线性增大趋势，而用钢量则近似双曲线性减小趋势，代表总工程造价相应减小。因此，在满足设计要求的情况下，应尽量选用用钢量曲线后半段所对应的加劲肋间隔值。同理，由于随加劲肋宽度增大，轨道梁竖向最大挠度近似线性增大而用钢量线性减小，因此，在满足设计要求条件下加劲肋宽度可选取0.1 m。

3.3 轨道梁各部分板厚

设单轨轨道梁跨度、加劲肋间距及加劲肋宽度固定，梁各部分板厚变化时梁的竖向最大挠度如图9所示。跨距仍为30 m，其中加劲肋间距取平均值1.05 m，取总段数n=51，则加劲肋宽度约为0.144 m，加劲肋槽宽t4取平均值0.15 m。

图9梁各部分板厚变化时梁的竖向最大挠度

图9 显示了当梁顶板、翼缘、走行面板板厚t1、t2、t3及加劲肋板厚t5在0.010～0.016 m范围内逐渐增大时，30 m跨度下轨道梁的竖向最大变形量随之近似呈线性减小趋势，但随加劲肋间距的增大而增大。在该跨度下所选取的任何加劲肋间距均能满足许用挠度条件。

比较t1、t2、t3、t5这4个参数，加劲肋板厚t5增大时梁的最大挠度减小最快，用钢量增加最缓慢；翼缘板厚t2增大时梁用钢量增加迅速，而最大挠度变化稍缓慢；顶板板厚t1增大时，梁的用钢量与最大挠度都处于中等变化速度；走行面面板厚t3增大时，梁用钢量增加次快，而最大挠度减小最为缓慢。因此，在满足经济性的同时，为尽量提高截面刚度、减小走行面局部翻转变形量［12］，加劲肋板应尽可能取较厚的板，t5宜取较大值，翼缘板厚t2可在满足强度条件下取较小值以减小整体用钢量；走行面板板厚t3增大所引起的最大挠度减小速度极其缓慢，但由于载荷在两相邻加劲肋之间的等刚度段内引起弯曲变形，尤其是走行面的翻转变形程度将极大地取决于t3值，因此，t3需在保证局部允许变形量的条件上尽量选取较小值。

3.4 加劲肋槽宽

设单轨轨道梁跨度、加劲肋间距及加劲肋纵向宽度固定，加劲肋内高变化时梁的竖向最大挠度如图10所示。其中：加劲肋间距取平均值1.05 m，总段数n=51，则加劲肋宽度约0.144 m，加劲肋槽宽t4取平均值0.15 m；梁顶板、翼缘、走行面板板厚t1、t2、t3及加劲肋板厚t5均取最小值10 mm，以便更大程度地对比出不同加劲肋槽宽时梁竖向最大挠度的变化。

图10 不同加劲肋槽宽下梁的竖向最大挠度

由图10可知，当加劲肋槽宽t4从0.1 m变化至0.2 m时，30 m跨度下轨道梁的竖向最大变形量近似呈线性减小趋势，而用钢量则近似呈线性增大趋势。在该跨度下所选取的任何加劲肋槽宽均能满足许用挠度条件。

4 结语

为分析加劲肋对梁整体挠度的影响，建立了静力载荷下超静定变截面梁的力学模型，以模拟其变刚度条件下的弯曲变形，并根据Matlab软件求解结果对悬挂式单轨轨道梁进行了尝试性结构优化设计。在取定轨道梁跨度为30 m和确定a、B、H尺寸组合的基础上，分别改变轨道梁加劲肋间距、宽度及梁各部分板厚，比较各种参数组合情况下的结果，得出在满足设计要求的情况下，30 m跨度时加劲肋间距为1.6 m、加劲肋宽度为0.1 m时轨道梁用钢量最少、造价相对合理的结论。同时，对梁各部分板厚的选取给出了相应建议，可为我国悬挂式单轨结构设计优化等设计工作提供参考。

［1］李芾，许文超，安琪.悬挂式单轨车的发展及其现状［J］.机车电传动，2014（2）：16-78.

［2］周庆瑞，金锋.新型城市轨道交通［M］.北京：中国铁道出版社，2005.

［3］辛建平.西德多特蒙德大学的高架悬挂客运系统［J］.铁道科技动态，1983（4）：13.

［4］潘西湘.悬挂式单轨系统轨道梁结构优化设计研究［D］.成都：学位论文，西南交通大学，2013.

［5］齊藤勝.湘南モノレール江の島線の概要［J］.新都市，1970，24（4）：55-59.

［6］YAMASAKI T，YANO T，HIKOAkA H.Curved steel guideway for suspended monorail system［C］//IABSE Congress Report.Zurich：IABSE，2014.

［7］上海市隧道工程轨道交通设计研究院.城市轨道交通设计规范：DGJ08-109—2004［S］.上海：上海市建设管理委员会，2004．

［8］李学军，朱萍玉，刘义伦.复杂载荷下变刚度静不定梁程序化求解［J］.工程力学，2003，20（4）：117-121.

［9］李学军，刘仪伦，朱萍玉.复杂载荷变刚度静不定梁通用力学模型及变形方程［J］.机械设计，2002，19（5）：11-13.

［10］李银山，杨维阳.变惯矩梁变形的函数解［J］.力学与实践，1992.14（2）：56-58.

［11］冯康，石钟慈.弹性结构的数学理论［M］.北京：科学出版社，1981.

［12］肖云霞，王月明，杨东晓，等.悬挂式单轨直线轨道梁结构优化设计探讨［J］.钢结构，2015，30（4）：68-71.

［13］北京钢铁设计研究总院.钢结构设计计算图表［M］.北京：冶金工业出版社，1983.

Deflection of Suspended Monorail Track Beam with Stiffeners

XIE Qian，WANG Yueming，JIANG Yongzhi，TAN Hongyuan

To study the impact of stiffeners of suspended monorail track beam over the overall deflection，a mechanical model of hyper-static tapered beams under static and live load is established to simulate the bending deformation of variable stiffness，from which the general equation of corner and bending deflection of arbitrary cross-section of the track beam is derived.Then，software Matlab is used to achieve the numerical solution of the maximum deflection of the beam，and the result is applied in an optimum design of the suspended monorail transit structure.

suspended monorail transit；track beam；stiffener；deflection

U213.2+13；U232

10.16037/j.1007-869x.2017.08.003

2015-09-25）