基于换乘网络的城市轨道交通客流分配模型*

黄鉴蒋赛

基于换乘网络的城市轨道交通客流分配模型*

黄鉴蒋赛

（西南交通大学交通运输与物流学院，610031，成都//第一作者，讲师）

城市轨道交通客流分配需要考虑乘客换乘的影响。为了直观表达乘客的换乘方案，方便换乘阻抗的计算，阐述了城市轨道交通换乘网络的构建方法，在分析换乘网络弧的阻抗计算方法的基础上，建立了城市轨道交通客流均衡分配模型。分析说明了该模型与公路交通分配模型具有相同的形式，因此可利用公路交通流分配算法进行求解。最后，通过实例验证了的该客流分配方法的有效性。

城市轨道交通；客流分配；换乘网络；换乘阻抗

Author′s addressSchool of Transportation and Logistics，Southwest Jiaotong University，610031，Chengdu，China

随着我国城市轨道交通建设的不断推进，城市轨道交通运营网络逐步形成，客流的网络化特征日趋明显，如何科学预测和研判城市轨道交通客流在空间上的分布规律，对提高城市轨道交通运营管理水平具有重要意义。对于“多运营商、多线路”的网络化运营城市，该问题的解决也为不同线路间的票务清分提供了分析手段。

目前，关于客流分配方面的研究多集中在公路交通分配方面，城市轨道交通网络客流分配的相关研究还不够成熟，研究成果多是借鉴公路交通分配的相关理论，如：文献［1］以轨道交通网络为基础，基于均衡分配原理，建立了客流量均衡分配模型，并采用Frank-Wolfe算法进行求解；文献［2-3］以城市轨道交通网络为基础，建立了客流分配的随机均衡模型并设计了相关算法；文献［4-5］研究了城市轨道交通客流的非均衡随机分配模型。上述研究成果在很大程度上促进了城市轨道交通客流分配相关理论的发展，然而这部分研究成果大多直接以轨道交通网络为基础建立客流分配模型，网络路径中对乘客换乘的表达不够直观，在一定程度了影响了现有交通分配理论在城市轨道交通客流分配中的应用。因此，本文试图以城市轨道交通线网为基础，通过构建乘客换乘网络，将城市轨道交通客流分配问题与公路交通流分配问题关联起来，从而实现城市轨道交通网络的客流分配问题的求解。

1 换乘网络的构建

1.1 基本假设

在构建乘客换乘网络之前，首先作以下基本假设。

（1）独立运营假设。除共用线路外，不同轨道交通线路之间的列车不得跨线运行。对于共用线路的情况，可将共用线路上的车站均视为两条线的换乘车站。如上海轨道交通3号线和4号线存在一段共用线路，即属于此类情况。

（2）同线不换乘假设。对于始发和终到站属于同一条单一线路的乘客，不考虑其在本线列车上的换乘。其中，单一线路是指“一”字型线路，即不存在支线的线路。

对于Y字型运营线路可采用分割处理方法将其转换为单一线路组合。比如图1所示的Y字型线路，假设运行交路为S1—S2—S3—S4和S1—S2—S3—S5，则S4至S5或S5至S4的乘客需要在S3站换乘本线列车方可到达，为了解决该问题，可将该Y字型线路分割为3条线路，分别为主线S1—S2—S3、支线S3—S4和S3—S5，同时将S3站视为换乘站。对于主线到支线、支线到主线的乘客均无需换乘，此时可将换乘时间视为0，对于支线之间的乘客需考虑换乘时间。对于其他复杂线路可参考“Y”字型线路的分割方法，将其转化为单一线路的组合。

图1 轨道交通“Y”字型线路示意图

（3）换乘节点假设。乘客只能在两条轨道交通线路相交的换乘站进行换乘，不考虑乘客在一般车站进行换乘的情况。

1.2 换乘网络的表达

换乘网络的节点包括车站节点和换乘节点，其中，车站节点为轨道交通线网中物理站点，换乘节点是根据换乘站可换乘的线路情况而扩展的节点，因此，换乘网络中增加的换乘节点数目等于线网中所有换乘站可换乘线路的代数和。换乘网络中的弧分为3类，分别为区间弧、换乘弧和关联弧，换乘弧与两个换乘节点相连，关联弧是指换乘节点与其关联车站的连接弧，其它均为区间弧。

假定由两条相交的轨道交通线组成的线网（如图2所示），分别为1号线的S1—S2—S3和2号线的S4—S2—S5，这2条线可通过S2站换乘，则可将该线网转变成为如图3所示的换乘网络。图2所示的线网中只有S2一个换乘车站，该车站可换乘的线路有2条，所以换乘网络中包含2个换乘节点，即S6和S7。

换乘网络中的路径包含换乘弧时，说明该路径需要乘客换乘，且路径中包含的换乘弧的个数等于换乘次数；另外，换乘网络中可不考虑节点费用，更无需根据路径中节点两侧弧的性质判断节点阻抗的取值。由于该换乘网络只针对换乘车站扩展节点，网络复杂度介于线网和服务网络［6］之间，对换乘方案的表达更清晰，也简化了路径阻抗的计算，适用于城市轨道交通线网客流分配。

例如，在图2中路径S4→S2→S3对应的乘车方案中，乘客需要在S2站换乘，但在路径中无法直观表达出来，且换乘时间需通过节点S2的阻抗加以体现，而节点S2的具体阻抗值又与路径中节点S2两侧的弧（S4，S2）和（S2，S3）是否属于同一条线以及具体的线路归属有关。对于同样的乘车方案，在换乘网络（图3）中可表达为S4→S7→S6→S3。由于路径中包含换乘弧（S7，S6），所以该方案需要乘客换乘，且换乘时间可利用该换乘弧的阻抗表达。

图2 两线相交的轨道交通线网示意图

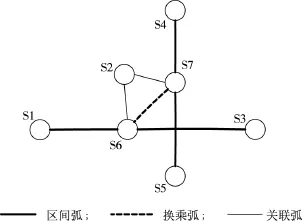
图3 两线相交的换乘网络示意图

2 换乘网络弧的阻抗

设换乘网络G=（N，A）。其中：N=N1∪N2为网络节点集合，N1为车站节点集合，N2为换乘节点集合；A=A1∪A2∪A3为网络中弧的集合，A1、A2、A3分别表示区间弧、换乘弧和关联弧的集合。对于任意弧a∈A，弧的阻抗记为Ra，弧的客流量记为xa。

2.1 区间弧的阻抗

区间弧的阻抗包括区间走行时间和拥挤折算时间两部分，其中区间走行时间可利用相邻两站间的距离和列车平均运行速度计算，另外，不失一般性，可将列车在区间起点的停站时间纳入区间走行时间，因此，区间走行时间可用式（1）计算。

式中：

da——区间长度；

va——列车在区间的平均运行速度；

tsa——列车在区间起始节点的停站时间。

拥挤折算时间是指由于拥挤而产生的额外时间耗费，主要从乘客的舒适度方面考虑。当列车上乘客数小于座位数时，乘客不会有不舒适感，此时拥挤折算时间为零；当乘客数大于座位数时，此时由于乘客必须站立甚至过度拥挤，由此拥挤系数可用式（2）表示［2］。式中：

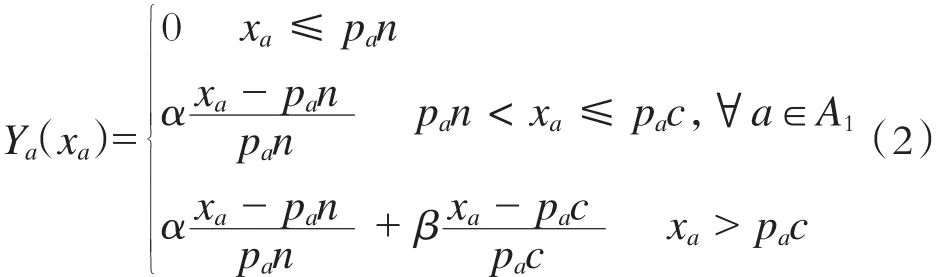
pa——区间列车服务频率；

xa——区间客流量；

n——列车座位数；

c——列车能容纳的最大乘客数；

α，β——校正系数，可通过调查数据统计回归得到。

不失一般性，还可将拥挤系数折算公式由线性函数扩展为幂函数形式，幂函数能更好地描述拥挤折算时间随客流增长的非线性关系［5］，如式（3）所示。

式中：

η，γ——校正系数。

根据以上分析，区间弧的总阻抗可采用式（4 a）计算。

2.2 换乘弧的阻抗

换乘时间包括换乘步行时间和换乘等待时间。换乘步行时间根据换乘通道的长度计算，换乘等待时间与换乘线路的平均发车间隔有关，可取发车间隔的1/2作为乘客的平均换乘等待时间。由于弧具有方向性，故不同方向上换乘弧的阻抗可以不同。另外，考虑到换乘过程中乘客的体力消耗等因素，在换乘和乘车中花费相同的时间产生的效果存在较大差异，在计算换乘弧的阻抗时对换乘时间乘以放大系数加以惩罚，因此对于换乘弧的阻抗可采用式（4 b）计算。

式中：

tba——换乘步行时间；

tia——换乘线路的平均发车间隔；

αn——换乘惩罚系数。

2.3 关联弧的阻抗

关联弧主要是为了表达换乘节点和车站节点之间的相互关联关系，不具备实际意义。为了避免利用换乘网络计算最短路径时通过关联弧绕过换乘弧，在此可取关联弧的阻抗为一个明显大于换乘弧的阻抗的实数M，如式（4 c）所示，具体取值不影响客流分配结果。

3 客流均衡分配模型及算法

对于给定的城市轨道交通换乘网络，用W表示起讫点（OD）对集合，KW表示OD对之间的所有路径集合w∈W，其中第k条路径包含的弧的集合记为Lw，k，qw表示OD之间的客流量，fw，k为KW路径集中第k条路径的客流量，σw，ka为0，1变量，σw，ka=1表示a∉Lw，k，否则，a∉Lw，k。据此建立基于换乘网络的城市轨道交通客流均衡分配模型如下：

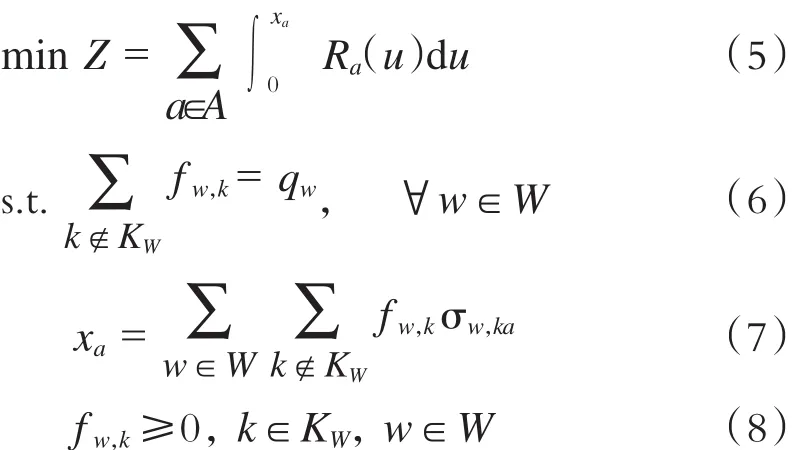
通过换乘网络中的换乘节点和换乘弧，将乘客的换乘时间表达成为换乘弧的阻抗，使得城市轨道交通客流分配符合公路交通流分配的特点（公路交通流分配无换乘问题），该模型与公路交通流均衡分配模型具有完全相同的形式。由模型可知，对于∀x≥0，函数Ra（x）连续，又因为因此目标函数Z相对于xa可微。模型满足Wardrop平衡条件，即任意分配流量的路径阻抗相等，且等于最短路径阻抗。因此，可利用相对成熟的公路交通流均衡分配算法进行求解，如Frank-Wolfe算法或连续平均算法等。

4 实例求解

为了进一步说明换乘网络的构建方法，同时检验客流分配结果，选取北京市已开通的轨道交通1号线、2号线、5号线组成的轨道交通线网为例，如图4所示。为了便于描述，图4网络中只列出了换乘站和主要车站，区间线路旁边的数字代表列车区间平均运行时间（min），将其转换为换乘网络后如图5所示。

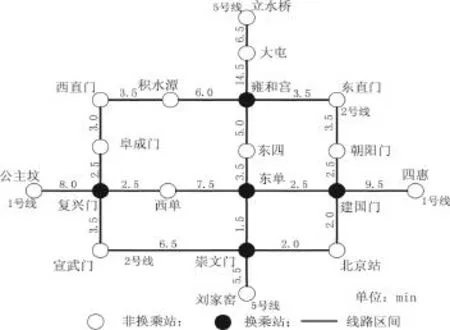
图4 北京轨道交通1、2、5号线网络

图5 北京轨道交通1、2、5号线换乘网络

为计算方便，选取了一些典型车站的高峰小时OD客流数据，并假定OD矩阵对称（如表1所示）。对于模型中各待定参数，通过调查数据及实测数据标定如下：列车发车频率15对/h，平均发车间隔4 min，列车座位数n=336人，列车容纳的最大乘客数c=2 370人，拥挤矫正参数α=1，β=2，列车平均停车时间40 s，平均换乘步行时间取5 min，换乘时间惩罚系数αn=1.6。

表1 北京轨道交通1、2、5号线典型车站的OD矩阵

根据用户均衡配流的Frank-Wolfe算法编程求解，各路段客流分配结果及各换乘站的换乘客流量分别如表2和表3所示，其中各换乘站的换乘客流量即为换乘网络中各换乘弧的分配客流量。由于客流分配结果是对称的，在此只列出了路段一个方向的客流分配结果，另外一个方向客流相同。

表2 各换乘站的换乘客流量人次

为了对计算结果的正确性进行验证，将北京站站至立水桥站的OD数据加倍，重新进行客流分配。根据路段客流分配结果的变化情况可以推测新增加的客流分配到了“北京站站—崇文门站—东单站—东四站—雍和宫站—大屯站—立水桥站”和“北京站站—建国门站—朝阳门站—东直门站—雍和宫站—大屯站—立水桥站”两个路径中。经计算，增加客流后这两个路径的阻抗分别为219.974 3和219.972 8，数值基本相等，达到了客流均衡分配的目的。

5 结语

通过构建城市轨道交通换乘网络，将城市轨道交通客流分配问题转化为与公路交通流分配具有相同形式的问题，方便了问题求解，同时还可根据换乘站的换乘客流量。该换乘网络不仅可以用于城市轨道交通均衡客流分配，还可应用于城市轨道交通其它客流分配方法的建模和计算。该客流分配方法不仅适用于已运营的不同轨道交通线路之间实际客流量的分配，对城市轨道交通规划设计阶段的客流分配预测也具有一定的参考价值。

表3 各路段客流分配结果人次

［1］吴祥云，刘灿齐.轨道交通客流量均衡分配模型与算法［J］.同济大学学报（自然科学版），2004，32（9）：1158-1162.

［2］四兵锋，毛保华，刘智丽.无缝换乘条件下城市轨道交通网络客流分配模型及算法［J］.铁道学报，2007，29（6)）：12-17.

［3］孔繁钰，陈小峰.轨道交通随机均衡配流模型和算法［J］.重庆工学院学报（自然科学版），2007，21（11）：26-30.

［4］徐瑞华，罗钦，高鹏.基于多路径的城市轨道交通网络客流分布模型及算法研究［J］.铁道学报，2009，31（2）：110-114.

［5］孙鸾英，王竞，蒲琪.基于随机网络加载的城市轨道交通客流分配模型［J］.城市轨道交通研究，2014，17（10）：115-118.

［6］于剑，徐彬.面向客流分配的城市轨道交通服务网络建模方法研究［J］.城市轨道交通研究，2014，17（9）：91-95.

Passenger Flow Distribution Model for Urban Rail Transit Based on Transfer Network

HUANG Jian，JIANG Sai

In the study of passenger flow distribution in urban rail transit，the impact of the transfer schemes shall be considered.To visually express the transfer schemes and calculate the traffic impedance，a construction method of transfer network for urban rail transit is proposed.Based on an analysis of the network arc impedance calculation，a model of equilibrium passenger flow distribution is established，which has the same form as the road traffic assignment model，and can be solved by traffic flow assignment algorithm.Finally，the effectiveness of the method is verified by numerous experiments on practical cases.

urban rail transit；passenger flow distribution；transfer network；traffic impedance

U293.6；U293.13

10.16037/j.1007-869x.2017.08.001

2015-11-27）

*中央高校基本科研业务费专项资金资助项目（2682014BR029）