基于K熵和关联维数的金属疲劳损伤过程的声发射信号特征分析

黄振峰, 刘永坚, 毛汉颖, 王向红, 李欣欣, 毛汉领

(1. 广西大学 机械工程学院, 南宁 530004； 2. 广西科技大学 汽车与交通学院, 广西 柳州 542506；3. 长沙理工大学 工程车辆安全性设计与可靠性技术湖南省重点实验室, 长沙 410004)

基于K熵和关联维数的金属疲劳损伤过程的声发射信号特征分析

黄振峰1, 刘永坚1, 毛汉颖2, 王向红3, 李欣欣1, 毛汉领1

(1. 广西大学 机械工程学院, 南宁 530004； 2. 广西科技大学 汽车与交通学院, 广西 柳州 542506；3. 长沙理工大学 工程车辆安全性设计与可靠性技术湖南省重点实验室, 长沙 410004)

深化对金属疲劳损伤过程中声发射信号的特征认识，是运用声发射信号对金属结构损伤过程进行监测预测的重要基础热点问题。针对金属疲劳损伤经历裂纹萌生阶段、裂纹缓慢扩展阶段、裂纹快速扩展阶段、临近破坏等四个阶段产生大量的声发射信号，采用K熵和关联维数等混沌特征量来分析海量的声发射信号；通过对45号钢试件进行三点弯曲疲劳试验、测试得到试件疲劳损伤过程的声发射信号，分别估算不同时间段所产生声发射信号的K熵和关联维数，分析结果表明金属疲劳损伤过程的声发射信号具有混沌特征，其K熵和关联维数的变化趋势与金属疲劳损伤过程的四个阶段具有较清晰的对应关联，表明K熵和关联维数可以较好的揭示金属疲劳损伤过程的动力学特性，这将为运用声发射信号实现金属结构疲劳损伤在线监测及预测提供了一种新思路。

声发射； 疲劳损伤； K熵； 关联维数

在交变载荷的作用下，材料或构件产生挤压变形，导致微裂纹形成，并且在裂纹尖端引起应力集中，进一步促使结构在较低的应力条件下发生裂纹扩展，随着裂纹的扩展最终发生断裂和失效。疲劳断裂突如其来，往往会给人们带来许多灾难性的事故。如何定性和定量地检测出材料的疲劳裂纹，并及时准确地对材料的疲劳损伤程度进行评估和预警预报，防止疲劳失效事故的发生，是目前从事材料检测工作的重点热点，也是难点。

材料或构件在产生塑性变形或有裂纹形成和扩展时，其应变能会以瞬态弹性波的形式释放出去，这种现象叫做声发射，利用声发射传感器采集损伤源的声发射波并以此对结构损伤程度做出判断，就是声发射损伤检测技术，具有灵敏度高、频响范围宽、信息量大、可动态检测等特点，在金属结构的缺陷检测和定位中显示了其优越性。大量学者展开了相关研究，如李光海等[1]利用声发射参数的变化来识别金属材料疲劳裂纹扩展的过程；Ennaceur等[2]利用声发射技术监测压力容器用钢的裂纹扩展，分析不同裂纹扩展阶段的AE参数特征，预测压力容器的剩余寿命；Robers等[3]研究了完整钢板和焊接钢板紧凑拉伸试验以及T型截面梁试验的疲劳裂纹扩展机制与声发射参数的关系；马桂英等[4]利用声发射技术，结合扫描电镜分析，对金属间化合物破断过程进行研究；李东生等[5]采集了多龄期斜拉索疲劳加载过程的声发射信号，利用参数分析法和小波分析法，得到多龄期斜拉索疲劳损伤的演化规律；张志强等[6]利用小波分析方法对铁基合金涂层疲劳损伤过程的声发射信号波形以及频率特征进行分析，实现对涂层接触疲劳损伤过程进行诊断和分析的目的。然而，大多数的研究对材料损伤程度的诊断往往只是做出定性的判断，而对于声发射信号特征与材料损伤程度、疲劳损伤过程的关联性研究相对较少。因此，研究声发射信号特征与材料损伤程度、疲劳损伤过程的关联性，对于声发射诊断和预测机理研究、准确快速地识别和诊断材料损伤程度具有重要意义。

试验研究表明，材料疲劳断裂过程产生的声发射信号呈现非线性、随机性、耗散性等特点。传统的线性理论分析方法不能很好揭示材料疲劳损伤过程。混沌理论特别适合处理复杂的非线性信号，且该理论日趋完善，广泛应用于机械设备故障诊断和状态监测中。蒋旭鑫等[7]计算了空气压缩机不同故障状态下的声发射信号的关联维数，发现该方法能有效诊断压缩机气阀的故障模式；Bukkapatnam等[8]提出一种基于混沌理论、小波分析和神经网络结合的新方法来分析机械不同运行状态的声发射信号；韩文兰等[9]研究了关联维数和最大Lyapunov指数与刀具磨损状态的联系；Takuma等[10]计算了剪切加工声发射信号的关联维数和最大Lyapunov指数，并用其来评估刀具的磨损状态和剩余寿命；成新民等[11]提取了转子碰摩声发射信号的关联维数、最大Lyapunov指数和Kolmogorov熵，并将这三者作为神经网络的输入，应用到碰摩声发射源的定位中。尽管诸多研究采用关联维数、Kolmogorov熵和Lyapunov指数等混沌特征来分析机械设备不同故障的声发射信号，但用来分析金属疲劳加载过程的声发射信号却鲜有提及。

本文通过采集金属结构疲劳损伤过程的声发射信号，利用累积声发射事件计数的实时变化初步判断了金属结构疲劳损伤程度，分别估算不同时间段金属疲劳损伤所产生声发射信号的K熵和关联维数，通过这两种混沌特征量研究揭示金属疲劳损伤过程，探索声发射信号特征与材料损伤程度、疲劳损伤过程的关联性，为预测预报金属结构疲劳损伤过程做机理研究。

1 K熵和关联维数的估计方法

1.1 K熵

Kolmogorov熵(简称K熵)是刻画混沌系统的一个重要的特征量。K=0时，表示系统作的是规则运动；K→∞时，表示系统作的是随机运动；K>0时，表示系统作的是混沌运动。K越大,信息的损失速率越大,系统的混沌程度越高,系统越复杂。目前计算K熵的方法主要有两种：一种是Grassberger等[12]提出的关联积分算法，另一种是Schouten等[13]提出的最大似然算法。由于最大似然算法计算比较简单，且整个计算速度比较快，所以本文采用最大似然算法来计算K熵，其计算过程如下。

不同轨道上初始邻近点之间的距离分离至其间距大于r0所需的时间呈指数分布：

c(t0)=e-Kbb=1,2,3,…

(1)

式中：K为K熵，b是初始间距小于r0的点对其间距首次超过r0时在相空间重构吸引子上所经历的演化时间步数。

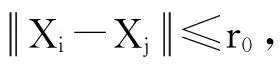
经过b步演化后找到初始邻近点之间距离大于r0的概率为:

P(b)=c(b-1)-c(b)=(e-k-1)e-kb

(2)

将上面的概率密度函数作归一化处理：

(3)

经过上面归一化后，在相空间中取出M对不相关的点，得到b1,b2,b3,…,bM和k的联合概率：

(4)

利用式(4)采用最大似然估计，可以得到K熵的最大似然估计值:

(5)

(6)

1.2 关联维数

关联维数刻画系统的非线性行为，描述系统的复杂程度，且关联维数值越大，系统越复杂。目前计算关联维数的主要方法是G-P算法[14]，其计算步骤如下：

Xi=(xi,xi+τ,…,xi+(m-1)τ)

(7)

Xj=(xj,xj+τ,…,xj+(m-1)τ)

(8)

则Xi和Xj之间在欧氏空间中的距离rij：

(9)

给定临界距离r，则距离rij小于r的点对数在所有点对数中所占的比例C(r)：

(10)

式中:N为总相点数；θ(x)为Heaviside函数；其定义为：

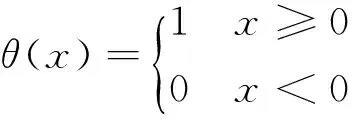
(11)

C(r)为关联积分，它刻画相空间中两点之间的距离rij小于r的概率，适当的调整r的取值范围，关联积分C(r)∝rD，D为关联维数，此时重构吸引子具有分形特征。关联维数D为

(12)

因此，要求出一个系统中存在的常数关联维数D，可以通过画出lnC(r)相对于lnr的双对数曲线，用最小二乘法拟合该曲线中相对较长的一段近直线部分的斜率，才能计算出关联维数的值。如果曲线的斜率对于逐渐增大的嵌入维数m逐渐收敛于一个饱和值，那么该值则为关联维数D。

2 金属疲劳试验及声发射信号测试

2.1 试验试样制备

选用45号钢作为三点弯曲疲劳试验的研究对象。根据国家标准GB/T 4161—2007，采用机械加工的方法从母材中加工出三点弯曲钢板试样3块，如图1(a)所示，三点弯曲试样的长L=120 mm，宽B=15 mm，高W=30 mm，采用线切割技术在试样中间预制一条长度为5 mm的机械缺口。

2.2 试验仪器与设置

疲劳加载系统采用长春科新试验仪器有限公司PX-20型高频疲劳试验机，声发射采集系统采用美国PAC公司PCI-2型双通道声发射测试系统，传感器型号为NANO-30，其中心频率为150 kHz，传感器布置在预制缺口的两侧，距离为60 mm，前置放大器选用2/4/6前置放大器，试验中选取前置放大器的增益为40 dB。图1(b)所示为三点弯曲疲劳加载过程声发射信号监测试验图。

(a) 三点弯曲试样

(b) 声发射信号监测试验

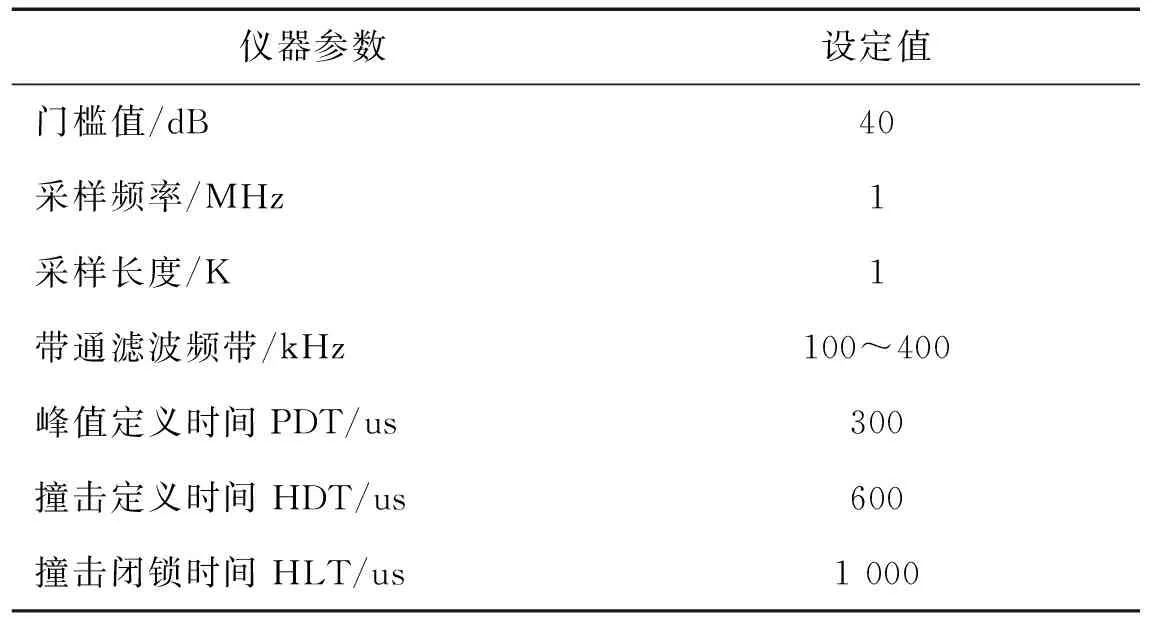
仪器参数设定值门槛值/dB40采样频率/MHz1采样长度/K1带通滤波频带/kHz100～400峰值定义时间PDT/us300撞击定义时间HDT/us600撞击闭锁时间HLT/us1000

实验开始前，声发射仪器按表1设置好实验参数，对试样预加载0.5 kN保证压头、试样及支承滚充分接触后，疲劳加载系统开始以正弦波形式施加载荷(最大载荷为13 kN，最小载荷为1.3 kN，频率为自适应频率)，同时采集AE信号直到实验结束。

3 试验数据分析

3.1 金属疲劳损伤过程的声发射特性

由于同种试样实验数据的宏观统计特性相似[15]，如材料损伤全过程中各AE参数在不同损伤阶段的变化范围、AE事件的变化规律等，因此，本节仅取一块试样的实验数据进行分析。

图2为45号钢疲劳损伤过程的累积声发射事件计数、频率与时间关系图。试件裂纹大小将影响疲劳试验机频率，裂纹越大，频率越小。在0～200 s之间，疲劳试验机的频率基本保持不变，累积声发射事件计数曲线以一定的斜率增长，为裂纹萌生阶段；在200～1 000 s，疲劳试验机的频率有一定的下降，但不明显，累积声发射事件计数曲线的斜率迅速减小，声发射事件计数比较平稳，裂纹缓慢平稳的向前扩展，这一阶段为裂纹缓慢扩展阶段；在1 000～1 600 s，疲劳试验机的频率逐渐下降，累积声发射事件计数曲线的斜率迅速增大，声发射事件计数反应强烈，裂纹加速扩展，这一阶段为裂纹快速扩展阶段；第1 600 s以后，由于试件临近破坏，疲劳试验机迅速卸荷，疲劳试验机的频率呈现直线下降的趋势，累积声发射事件计数增长缓慢，声发射事件计数比较小，这一阶段为临近破坏阶段。

可以看出，声发射信号在发生速率、累积声发射事件计数以及疲劳试验机加载频率曲线的斜率等均具有明显的阶段性特征，而且在时间上吻合得很好，说明累积声发射事件计数的变化可以反映45号钢疲劳损伤的不同程度。

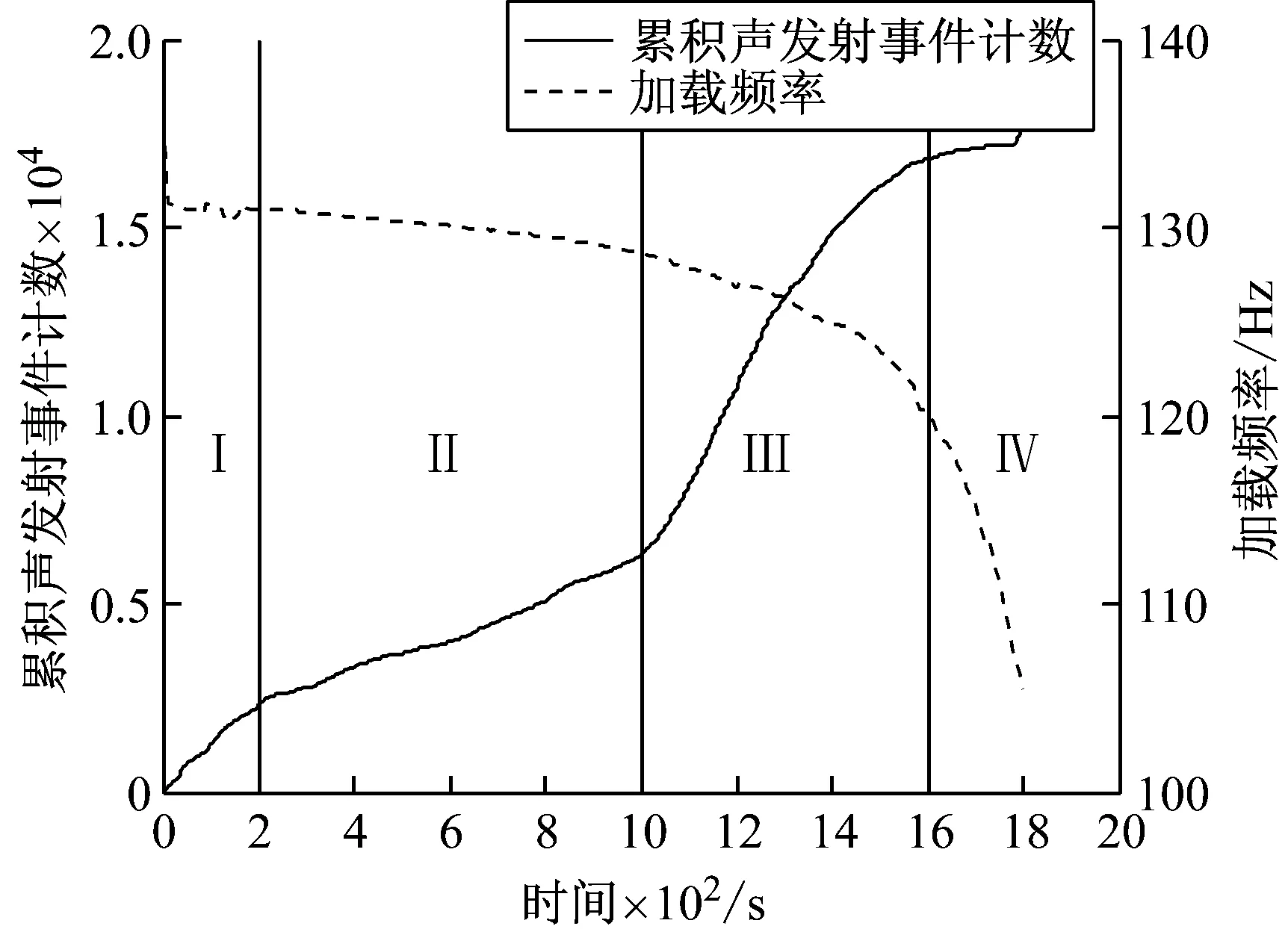
图2 累积声发射事件计数-时间-加载频率

3.2 Kolmogorov熵结果分析

选取12个45钢疲劳损伤过程不同时间段，每个时间段分别取10组数据，采用最大似然算法求取这10组数据的关联维数，并对计算结果进行平均，则均值为该时间段的K熵值，其变化曲线图如图3所示。由图3的不同时间段的K熵变化曲线图可以看出，金属疲劳损伤过程的K熵均大于0，说明金属疲劳损伤过程的声发射信号具有混沌特征。在裂纹萌生阶段、裂纹缓慢扩展阶段、裂纹快速扩展阶段，K熵呈增长趋势，裂纹尖端的扩展状态越来越复杂，信号的混沌程度逐渐增强；在裂纹快速扩展阶段后期即金属临近破坏之前，K熵达到最大值。在金属临近破坏阶段，K熵呈减小的趋势，信号的混沌程度逐渐减弱，这与此阶段，疲劳试验机逐渐卸荷，加载力逐渐减小，金属裂纹扩展活动逐渐减弱，声发射事件数较少相吻合。K熵在金属临近破坏前先升后降，据此K熵可以作为金属临近破坏的识别特征。

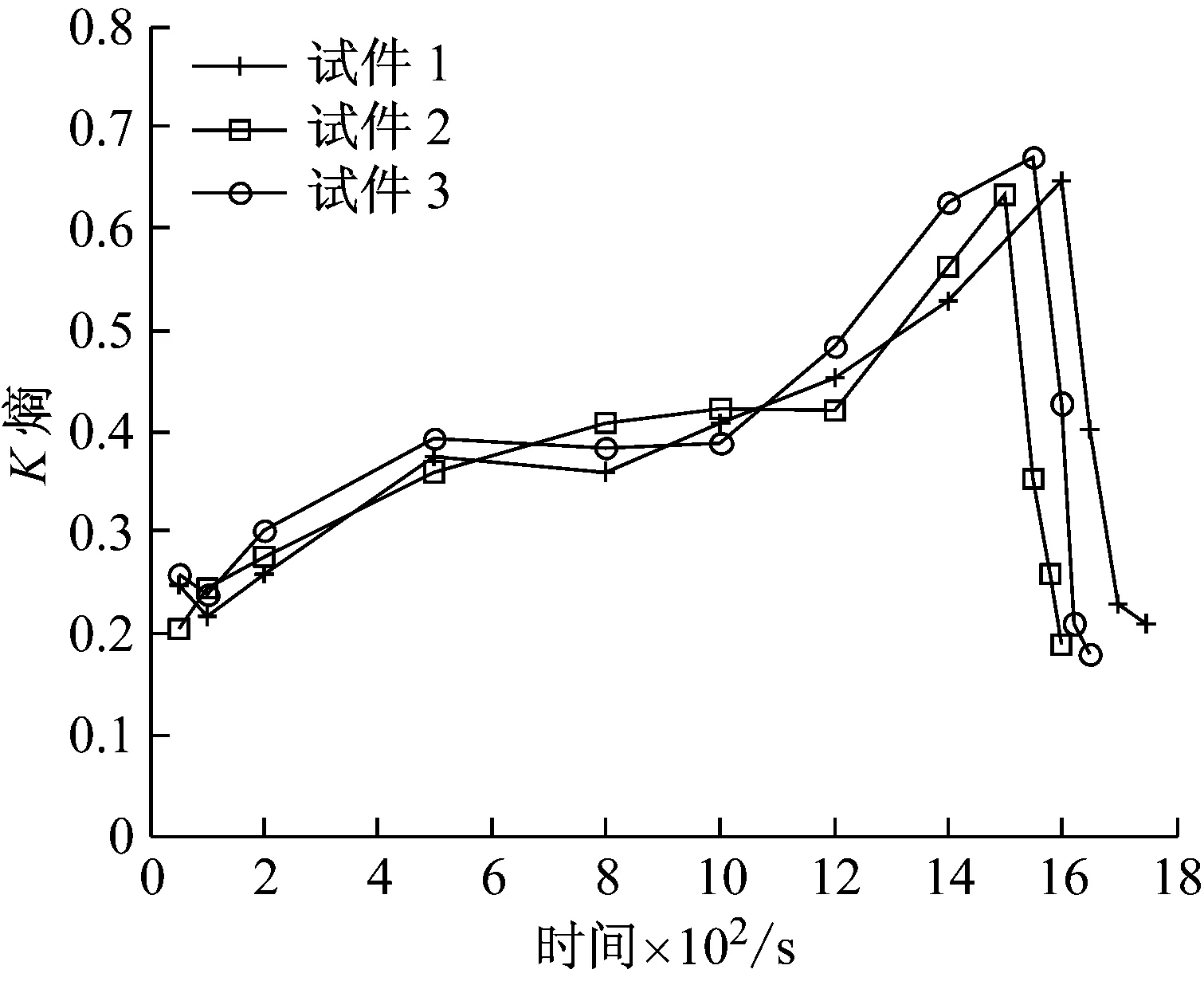
图3 K熵计算结果

3.3 关联维数结果分析

同样选取12个45钢疲劳损伤过程不同时间段，每个时间段分别取10组数据，采用G-P算法求取这10组数据的关联维数，并对计算结果进行平均，则均值为该时间段的关联维数值，其变化曲线图如图4所示。由图4可知，金属在不同的损伤状态下，其声发射信号的关联维数不同。和K熵的变化规律一致，关联维数在裂纹萌生阶段、裂纹缓慢扩展阶段、裂纹快速扩展阶段虽然有起伏，但是呈现逐渐增加的趋势，在裂纹快速扩展阶段后期即金属临近破坏之前达到最大值。在金属临近破坏阶段，关联维数呈下降趋势，这与此阶段，疲劳试验机逐渐卸荷，加载力逐渐减小，金属裂纹扩展活动逐渐减弱，声发射事件数较少相吻合。

图4 关联维数计算结果

3.4 裂纹扩展机理分析

从裂纹扩展的机理来看，由于在试件的中间用线切割技术加工了一道机械缺口，所以试件中间的缺口处局部应力最大，而外载荷作用在试件的中间，在外载荷的循环作用下，试件受到外载荷、两边支承辊的支撑力以及两边支承辊的摩擦力作用。在实验刚开始的时候，机械缺口处在交变应力的作用下，金属材料产生了位错滑移，晶格发生扭曲，晶粒产生破裂，这种现象在交变应力的继续作用下不断出现，直到在机械缺口处失去塑性变形的能力而形成疲劳裂纹源，即疲劳裂纹成核，此阶段声发射信号较少，K熵和关联维数的数值较小。裂纹萌生以后主要是沿着金属材料塑性变形的方向扩展，在裂纹扩展阶段，虽然也有塑性变形发生，但是这一阶段的主要物理过程表现为各个孔洞之间的连通。在裂纹缓慢扩展阶段，孔洞不断积累长大，但过程比较缓慢而均匀，孔洞之间的连通速度也比较缓慢，此阶段声发射活动性增强，声发射信号比较丰富，K熵和关联维数的数值有所增加。在裂纹快速扩展阶段，孔洞之间的连通速度逐渐加快，在表面含有很多与正应力方向相同的撕裂棱，此阶段声发射活动性最强，声发射信号也最丰富，K熵和关联维数的数值达到最大值。在金属临近破坏阶段，疲劳试验机逐渐卸荷，加载力逐渐减小，金属裂纹扩展活动逐渐减弱，K熵和关联维数的数值呈下降的趋势。

4 结 论

(1) 搭建金属三点弯曲试样疲劳加载过程声发射监测试验平台，获得金属疲劳损伤过程的声发射信号；通过对金属疲劳损伤过程的累积声发射事件计数的分析，识别含有机械缺口的45号钢疲劳损伤过程的四个不同阶段：裂纹萌生阶段、裂纹缓慢扩展阶段、裂纹快速扩展阶段、临近破坏阶段。

(2) 应用K熵和关联维数对声发射信号进行分析，结果表明，金属疲劳损伤过程的声发射信号存在混沌现象，且金属在不同疲劳损伤程度，其混沌特性变化与疲劳损伤过程有较强的关联性，表现为：在裂纹萌生阶段、裂纹缓慢扩展阶段、裂纹快速扩展阶段，K熵和关联维数都呈逐渐增加的趋势；在金属临近破坏阶段，两者都呈逐渐减小的趋势，声发射信号的K熵和关联维数可以作为表征金属疲劳损伤程度的特征量。

[1] 李光海, 刘正义. 基于声发射技术的金属高频疲劳监测[J]. 中国机械工程, 2004, 15(13):1205-1209.

LI Guanghai, LIU Zhengyi. Inspection of metal high frequency cyclic fatigue behavior utilizing acoustic emission technique[J].China Mechanical Engineering,2004,15(13):1205-1209.

[2] ENNACEUR C，LAKSIMI A，HERVE C，et al．Monitoring crack growth in pressure vessel steels by the acoustic emission technique and the method of potential difference[J].International Journal of Pressure Vessels and Piping，2006，83(3): 197-204．

[3] ROBERTS T M, TALEBZADEH M. Acoustic emission monitoring of fatigue crack propagation[J]. Journal of Constructional Steel Research, 2003, 59(6):695-712.

[4] 马桂英, 孔凡公, 邹蓉,等. 金属间化合物破断过程的声发射研究[J]. 机械工程材料, 2003(10):20-22.

MA Guiying, KONG Fangong, ZOU Rong, et al. A study of the fracture process of intermetallic compounds using acoustic emission technology[J].Materials for Mechanical Engineering,2003(10):20-22.

[5] 李冬生, 胡倩, 李惠,等. 多龄期桥梁斜拉索疲劳损伤演化声发射监测技术研究[J]. 振动与冲击, 2012, 31(4):67-71.

LI Dongsheng, HU Jing, LI Hui, et al.Acoustic emission technique for monitoring stay cable fatigue damage evolution of multi-aged bridge[J].Journal of Vibration and Shock,2012,31(4):67-71.

[6] 张志强, 李国禄, 王海斗,等. 涂层接触疲劳损伤过程中的声发射小波分析[J]. 材料工程, 2012(9):48-53.

ZHANG Zhiqiang, LI Guolu, WANG Haidou, et al. Acoustic emission wavelet analysis of coating during contact fatigue damage process[J].Journal of Materials Engineering,2012(9):48-53.

[7] 蒋旭鑫, 曹军义, 李锐,等. 基于声发射和关联维数的空气压缩机故障诊断技术研究[J]. 机械强度, 2011(6):803-808.

JIANG Xuxin, CAO Junyi, LI Rui, et al. Fault diagnosis of air compressor based on AE signals and correlation dimension[J].Journal of Mechanical Strength,2011(6):803-808.

[8] BUKKAPATNAM S T S, KUMARA S R T, LAKHTAKIA A. Analysis of acoustic emission signals in machining[J]. Asme Journal of Manufacturing Science & Engineering, 1999, 121(4):568-576.

[9] 韩文兰, 席剑辉. 刀具声发射信号混沌特征提取及趋势分析[J]. 沈阳航空航天大学学报, 2011, 27(4):74-78.

HAN Wenlan, XI Jianhui. Chaotic characteristics extracting and trend analysis on acoustic emission signal of tool condition[J].Journal of Shenyang Aerospace University,2011, 27(4):74-78.

[10] TAKUMA M, SHINKE N, NISHIURA T, et al. Acoustic emission evaluation systems of tool life for shearing of piano and stainless steel wires[J]. Journal of Acoustic Emission, 2006(24):52-66.

[11] 成新民, 胡峰, 邓艾东,等. 基于混沌理论的碰摩声发射特征分析与源定位[J]. 中国机械工程, 2011(9):1013-1017.

CHENG Xinmin, HU Feng, DENG Aidong, et al. Characteristic analysis and localization of acoustic emission source based on chaos theory[J].China Mechanical Engineering,2011(9):1013-1017.

[12] GRASSBERGER P, PROCACCIA I. Characterization of strange attractors[J]. Phys.Rev.Lett.A, 1983, 50(5):346-349.

[13] SCHOUTEN J C, TAKENS F, VAN C M, et al. Maximum-likelihood estimation of the entropy of an attractor[J]. Phys. Rev. E, 1994, 49(1):126-129.

[14] GRASSBERGER P, PROCACCIA I. Measuring the strangeness of strange attractors[J]. Physica D Nonlinear Phenomena,1983, 9(1/2):189-208.

[15] 张一辉, 张文斌, 许飞云,等. Q235B钢板拉伸损伤试验的声发射特性[J]. 振动与冲击, 2015, 34(15):156-161.

ZHANG Yihui, ZHANG Wenbin, XU Feiyun, et al. Acoustic emission characteristics of Q235B steel plates’ tensile damage tests[J].Journal of Vibration and Shock,2015,34(15):156-161.

Feature analysis for acoustic emission signals during metal fatigue damage based on Kolmogorov entropy and correlation dimension

HUANG Zhenfeng1, LIU Yongjian1, MAO Hanying2, WANG Xianghong3, LI Xinxin1, MAO Hanling1

(1. College of Mechanical Engineering, Guangxi University, Nanning 530004,China;2. College of Automobile and Transportation, Guangxi University of Science and Technology, Liuzhou 542506,China； 3. Hunan Province Key Laboratory of Safety Design and Reliability Technology for Engineering Vehicle, Changsha University of Science and Technology, Changsha 410004,China)

Deeply knowing features of acoustic emission (AE) signals during metal fatigue damage is a basic and hot key for adopting AE signals to detect metal structures’ damages. Aiming at a great amount of AE signals produced in four stages of metal fatigue damage including crack initiation, slow crack propagation, rapid crack propagation and approaching failure, they were analyzed with Kolmogorov entropy and correlation dimension. AE signals were measured in three-point bending tests of 45# steel specimens. Kolmogorov entropy and correlation dimension of the measured AE signals at different time durations were estimated. It was shown that AE signals during metal fatigue damage have chaotic features, the change trends of their K-entropies and correlation dimensions have clear relations to the four stages of metal fatigue damage; so K-entropy and correlation dimension can be used to better reveal the dynamic characteristics of metal fatigue damage processes. The results provided a new idea for online monitoring and predicting metal structures’ fatigue damage with AE signals.

acoustic emission (AE); fatigue damage; Kolmogorov entropy; correlation dimension

国家自然科学基金(51365006; 51445013; 51105045); 广西制造系统与先进制造技术重点实验室课题(14-045-15S05)。

2016-01-25 修改稿收到日期：2016-06-07

黄振峰 男，教授，1963年10月生

毛汉领 男，博士，教授，1963年11生

E-mail:maohl79@gxu.edu.cn

TG115.28

A

10.13465/j.cnki.jvs.2017.15.031