三相邻结构的减震效果分析

刘良坤， 谭 平， 闫维明， 周福霖,

(1.北京工业大学 建筑工程学院，北京 100124； 2.广州大学 工程抗震研究中心，广州 510405)

三相邻结构的减震效果分析

刘良坤1， 谭 平2， 闫维明1， 周福霖1,2

(1.北京工业大学 建筑工程学院，北京 100124； 2.广州大学 工程抗震研究中心，广州 510405)

提出对三个相邻结构间连接阻尼装置进行减震控制，推导了其单自由度简化模型随机响应计算公式，同时也给出了多自由度模型的阻尼、刚度等矩阵的构造方法并利用复模态法推导了其随机响应公式；最后对单自由度简化模型的三相邻结构各组合情况的减震效果分别进行了分析，并详细研究一般情况下的多自由度模型的三相邻结构减震效果。经仿真分析表明，三相邻结构控制后与两相邻结构控制所得结果基本相同；在两相邻结构对称而控制无效的情况下，三相邻结构仍可得到较好的控制效果；三相邻结构具有良好的鲁棒性，且对高阶响应峰值抑制明显。

相邻结构；复模态；对称；控制；鲁棒性

近年来，城市用地紧张，不少高层结构不可避免地面临处理楼间距的问题；而且当结构体型过大，结构特殊时也常需考虑设缝；为了防止结构碰撞，抗震规范给出了一定标准，卢明奇等[1]通过各类场地等条件下的大量地震波对结构的响应作了分析研究，给出了地震作用下相邻结构的最大相对位移计算公式，然而结构减震的问题并未解决。翟长海等[2-3]讨论了两相邻结构碰撞问题，但更多的时候，我们并不希望结构碰撞，那么如何既利用好有限的楼间距，又能防止碰撞同时减少结构自身的振动，这正逐渐成为一个研究热点。Xu等[4-5]进行了相邻结构间弹簧和阻尼器减震参数的分析，利用虚拟激励法和复模态法分析表明：使用最优参数可以获得最大的模态阻尼比并使结构响应最小；装有Maxell型阻尼器的结构同样可以得到较好的减震效果[6]，并且减震结构的特性与安装Viogt黏弹性阻尼器类似[7]。朱宏平等[8-10]利用能量法得到了两自由度简化模型的最优参数解析式，对具有质量，刚度等不确定因素的相邻结构分析表明，采用最优参数时，被控制的相邻结构具有很好的鲁棒性[11]。相邻结构的阻尼减震控制效果较好，关于其最优参数的研究也比较多，Richardson等[12]利用相邻结构的封闭解及类似于TMD的优化方式得到其最优参数的计算公式。Ok等[13-14]对具有非线性滞回特性的阻尼器进行了优化，结果也表明其具有较好的减震性能。除了连接被动控制装置，不少研究者也热衷于主动、半主动控制甚至混合控制[15-18]，并且其减震效果常优于一般的被动控制。

两相邻结构的控制研究相对成熟，但实际结构中常常出现的是三结构相邻的情况，比如具有两个裙房的主塔楼，或两塔楼加裙房；又比如奇数个结构相邻，当采用两结构相邻控制时总有一个结构需要单独处理，因此，对于三相邻结构的研究是非常有必要的。目前这方面的研究非常少，最近的文献仅发现Kim等[19]分析了安装黏弹性的三相邻对称结构在控制下的减震性能。本文将对三相邻结构控制模型的减震特性做初步的探索。

1 单质点简化分析模型

与两相邻结构控制一样，当仅考虑每个结构的第一振型时，可将其简化成单自由度结构，那么三相邻结构控制简化后，可采用三质点系模型如图1(b)所示(本文所研究的结构均假定为层剪切模型)。若采用Kelvin控制模型，相应的运动微分模型如下:

(a) 多自由度层模型简图

(b) 单质点模型简图

(1)

式中:k1，c1为结构L与C的连接等效刚度与等效阻尼系数；k2，c2为结构C与R的连接等效刚度与等效阻尼系数；mj，cj，kj(j=L,C,R)为结构L，C，R的质量，阻尼，刚度参数。现作如下假定：

代入式(1)并经傅氏变换可得结构的传递函数，若取：

传递函数则可表示如下

(2)

(3)

同样地，可以计算相应的速度与绝对加速度方差。

2 多质点分析模型

总阻尼矩阵如下表示：

其中，非耦联阻尼矩阵如下表示：

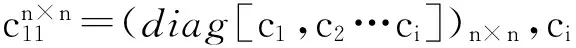
总刚度矩阵表示为

其中，各耦联结构刚度矩阵及非耦联刚度矩阵构造方式与阻尼矩阵的构造处理类似，此处也不作详细描述。

(4)

状态方程(4)对应的特征矢量方程如下：

[Meλ+Ke]Φ=0

(5)

(6)

(7)

(8)

相应地结构响应均方差为

(9)

类似地，相应的速度与绝对加速度方方差也可求得。

3 减震效果分析

3.1 单质点模型

(10)

这四种常见组合按以下几种情况进行分类

1) 对称

组合1：中间结构C较刚，结构L与R柔，由于对称性，只对比L与C即可，R与C类似。

组合2：中间结构C较柔，左右两边结构L与结构R较刚刚，由于对称性，只对比L与C，R与C类似。

组合3：L与C(或R与C)部分对称，结构R(L)参数任意，这里分析时只取一种情况，即L与C对称而R参数任意，由于对称性，另外一种情况只需更换符号即可。

2) 非对称

组合4：除以上对称的3种情况，结构L，C，R参数任意。

表1 参数选取

根据表1列出的结构参数值及控制参数优化范围，优化后可得到各组合最优参数下的减震系数，本文主要讨论控制效果，由于数据信息较多有关最优控制参数的情况将不全部列出，仅在分析涉及时给出。图2～图5分别是各组合的减震系数随fL(fR)的变化曲线，其中，LCRL表示三相邻结构LCR控制下结构L的减震系数，LCL即是两相邻结构LC控制下结构L的减震系数，后文中其他表达方式含义类似。图2为组合1的减震系数随fL(fR)的变化曲线，观察图2(a)，显然三相邻结构LCR全对称情况下的控制与两相邻结构LC控制，对结构L的控制效果基本一致，仅略有差异，图3(a)的组合2的情况也能得出同样的结论，这表明全对称的三相邻结构LCR可以和相应的两相邻结构LC控制达到一样的控制效果。图2(b)的组合1与图3(b)的组合2对结构C的控制情况也证实了上述的结论。

图4则给出了组合3(部分对称)的情况，显然对于三相邻结构是部分对称的，而两相邻结构LC则是完全对称的。从控制效果来看，此时两相阾结构对称，频率相同而无相对位移，控制装置不能进行工作，耗能无效，此时几乎无控制作用；而三相邻结构的控制效果则非常好，弥补了两相邻结构对称情况下的不足，仅在接近频率比fR=1(此时三相邻结构全对称)时表现出无控制作用，但只要使其中一个结构频率与其余两个有差别都将具有一定的减震作用。

(a) 结构L减震系数随频率比关系

(b) 结构C减震系数随频率比关系

Fig.2 Case 1: StructureCis relatively rigid and bothLandRare soft

(a) 结构L减震系数随频率比关系

(b) 结构C减震系数随频率比关系

Fig.3 Case 2: StructureCis relatively soft and bothLandRare rigid

为了了解更一般的情况，通过变换非对称三相邻结构L和R的频率比得到不同情况的最优参数，绘出减震效果如图5所示，从图5中可以发现，三相邻结构LCR在取得最优控制参数后的控制效果与两相邻结构LC(或结构CR)单独控制的效果基本接近，这与图2与图3的所分析结果相同，仅在接近fL=fR=1(三相邻结构、两相邻结构均对称)时，几乎无减震效果，但对于三相邻结构，只要有其中一结构偏离频率比为1就可获得比两相邻结构更好的结果。此外，需要注意的，虽然图5分析的三相邻结构LCR的质量不相同，但其控制效果仅与各自的固有频率有关，只要结构的固有频率相近控制效果就会大打折扣；不过这里的分析仅仅采用了简化的单自由度模型，考虑到实际结构的质量分布，刚度分布的差异不一定得到此结论，因此，正如上一节所述，在实际处理时需要采用多自由度结构来计算。

(a) 结构L减震系数随频率比关系

(b) 结构C,R减震系数随频率比关系

Fig.4 Case 3: StructureLandCare symmetry andRis any case

3.2 多质点模型

上节分析了单自由度模型的减震情况，而对于实际结构，受到质量，刚度等影响，高阶振型是不容忽视的。此节将采用实际案例来对多质点模型进行分析。 某三相邻结构LCR的阻尼比均为0.02，未控制的三个相邻结构采用瑞雷阻尼计算。其中结构L有15层，每层质量为1.0E+006 kg，刚度为2.5E+009 N/m；结构C有17层，每层质量为1.5E+006 kg，刚度为2.8E+009 N/m；结构R有20层，每层质量为1.5E+006 kg，刚度为2.2E+009 N/m。所采用的控制方案为：相邻结构各楼层处均安装减震装置，为分析方便，所取参数均为相同。随机分析时利用文献[4]的数据，谱密度S0=4.65×10-4m2/rad·s3，其余参数为ωg=15.0 rad/s，ξg=0.6，ωk=1.5 rad/s，ξk=0.6。时程分析时，选用EL-centro地震波，按8度基本设防烈度设计，取加速度幅值为0.2 g。其中输入地震功率谱模型如下

(a) 结构L减震系数与频率比fL，fR三维图(三维曲面LCRL，三维网格LCL)

(b) 结构C减震系数与频率比fL，fR三维图(三维曲面LCRC，三维网格LCC)

(c) 结构R减震系数与频率比fL，fR三维图(三维曲面LCRR，三维网格CRR)

(d) 结构C减震系数与频率比fL，fR三维图(三维曲面LCRC,三维网格CRC)

若结构的控制参数优化范围取ξ1,ξ2∈[0.01,0.3]，f1,f2∈[0.0,0.5]，经优化后得到三相邻结构的最优参数[ξ1,ξ2,f1,f2]=[0.3,0.29,0.47,0.22]，结构L,C,R减震系数为[0.202 9,0.287 8,0.424 8]；两相邻结构LC最优参数[ξ1,f1]=[0.13,0]；同样的，相应的两相邻结构L,C减震系数为[0.318 4,0.457 2]；两相邻结构CR最优参数[ξ1,f1]=[0.15,0]，相应减震系数为[0.351 2,0.459 6]。分析这些数据，可知此算例中，随机激励下，较两相邻结构，三相邻结构控制可以取得更好的减震效果。

图6比较了最优参数下三相邻结构控制与未控制(图中结构L,C,R)的响应功率谱，不管是位移还是加速度，从谱密度来看，三相邻结构控制可在很大程度上削弱其未控制情况下的峰值，而且对高阶的峰值也有较好地抑制作用，这说明三相邻结构在控制后具有较好的鲁棒性。图7进一步论证了实际地震波下的良好控制效果，通过与未控制的三相邻结构、控制的两相邻结构对比，发现三相邻结构对加速度的控制效果均更好，仅对R结构控制时中部楼层略有放大；而对位移的控制上三相邻结构控制略差于两相邻结构控制效果，但对R的控制效果好些，这与本文中采用绝对加速度的减震系数作为优化目标有关。

(a) 顶层位移功率谱

(b) 顶层绝对加速度功率谱

4 结 论

本文提出对三个相邻结构进行控制，根据两相邻结构的简化方法，将三相邻结构简化为单自由度模型，并推导了随机响应计算公式；为更合理地分析，又推导了多自由的三相邻结构运动方程，给出了阻尼、刚度等矩阵的构造方式，并利用复模态推导随机响应公式。

(a) 结构L

(b) 结构C

(c) 结构R

(d) 结构L

(e) 结构C

(f) 结构R

经仿真分析表明：

(1) 三相邻结构的控制即使在对称的情况下，其控制效果也接近相应的非对称情况下两相邻结构控制效果。

(2) 当两相邻结构对称时，几乎无控制效果，但三相邻结构仍可得到较好的控制，仅当其三个结构频率都相同时才无控制效果。

(3) 三相邻结构具有良好的鲁棒性，对多阶谱密度响应峰值具有削弱作用；在实际地震动作用下也能得到较好的控制效果。

由于控制参数信息量大，限于篇幅，本文减少了对控制参数分析，这一方面以及三相邻结构相互之间的能量传递情况有待进一步探究。

[1] 卢明奇, 杨庆山. 地震作用下相邻建筑结构的最大相对位移[J]. 土木工程学报, 2012(3):74-78.

LU Mingqi, YANG Qingshan, Maximum relative displacement between adjacent structures[J]. China Civil Engineering Journal, 2012(3):74-78.

[2] ZHAI C, JIANG S, LI S, et al. Dimensional analysis of earthquake-induced pounding between adjacent inelastic MDOF buildings[J]. Earthquake Engineering & Engineering Vibration, 2015, 14(2):295-313.

[3] 翟长海, 蒋姗, 李爽,等. 地震作用下相邻建筑结构碰撞反应分析[J]. 土木工程学报, 2012(增刊2):142-145.

ZHAI Changhai, JIANG Shan, LI Shuang, et al. Analysis of earthquake-induced pounding for two adjacent building structures[J]. China Civil Engineering Journal, 2012(Sup2):142-145.

[4] XU Y L, HE Q, KO J M. Dynamic response of damper-connected adjacent buildings under earthquake excitation[J]. Engineering Structures, 1999, 21(2):135-148.

[5] ZHANG W S, XU Y L. Dynamic characteristics and seismic response of adjacent buildings linked by discrete dampers[J]. Earthquake Engineering & Structural Dynamics, 1999, 28(10):1163-1185.

[6] ZHU H P, XU Y L. Optimum parameters of Maxwell model-defined dampers used to link adjacent structures[J]. Journal of Sound & Vibration, 2005, 279(1-2):253-274.

[7] ZHANG W S, XU Y L. Vibration analysis of two buildings linked by maxwell model-defined fluid dampers[J]. Journal of Sound & Vibration, 2000, 233(5):775-796.

[8] 朱宏平, 俞永敏,唐家祥. 地震作用下主-从结构的被动优化控制研究[J]. 应用力学学报, 2000, 17(2):63-69.

ZHU Hongping, YU Yongmin, TANG Jiaxiang. Optimal passive control of primary-auxiliary structures under earthquake excitation[J]. Chinese Journal of Applied Mechanics, 2000, 17(2):63-69.

[9] ZHU H, WEN Y, IEMURA H. A study on interaction control for seismic response of parallel structures[J]. Computers & Structures, 2001, 79(2):231-242.

[10] 黄潇, 朱宏平. 地震作用下相邻结构间阻尼器的优化参数研究[J]. 振动与冲击, 2013, 32(16):117-122.

HUANG Xiao, ZHU Hongping. Optimum parameters of dampers interconnecting adjacent structures under earthquakes[J]. Journal of Vibration and Shock, 2013, 32(16):117-122.

[11] GE D D, ZHU H P, WANG D S, et al. Seismic response analysis of damper-connected adjacent structures with stochastic parameters[J]. Journal of Zhejiang Universityence A, 2010, 11(6):402-414.

[12] RICHARDSON A, WALSH K K, ABDULLAH M M. Closed-form equations for coupling linear structures using stiffness and damping elements[J]. Structural Control & Health Monitoring, 2013, 20(3):259-281.

[13] OK S Y, SONG J, PARK K S. Optimal design of hysteretic dampers connecting adjacent structures using multi-objective genetic algorithm and stochastic linearization method[J]. Engineering Structures, 2008, 30(5):1240-1249.

[14] BASILI M, ANGELIS M D. Optimal passive control of adjacent structures interconnected with nonlinear hysteretic devices[J]. Journal of Sound & Vibration, 2007, 301(1/2):106-125.

[15] NG C L, XU Y L. Semi-active control of a building complex with variable friction dampers[J]. Engineering Structures, 2007, 29(6):1209-1225.

[16] PARK K S, OK S Y. Hybrid control approach for seismic coupling of two similar adjacent structures[J]. Journal of Sound & Vibration, 2015, 349:1-17.

[17] BHARTI S D, DUMNE S M, SHRIMALI M K. Seismic response analysis of adjacent buildings connected with MR dampers[J]. Engineering Structures, 2010, 32(8):2122-2133.

[18] YING Z G, NI Y Q, KO J M. Stochastic optimal coupling-control of adjacent building structures[J]. Computers & Structures, 2003, 81(30/31):2775-2787.

[19] KIM J, RYU J, CHUNG L. Seismic performance of structures connected by viscoelastic dampers[J]. Engineering Structures, 2006, 28(2):183-195.

Aseismic control effect analysis for three adjacent structures

LIU Liangkun1, TAN Ping2, YAN Weiming1, ZHOU Fulin1,2

(1. College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China; 2. Earthquake Engineering Research & Test Center, Guangzhou University, Guangzhou 510405, China)

Using damping devices connected among three adjacent structures to implement their aseismic control was proposed here. The random response formula was derived based on a single-DOF system simplified model for three adjacent structures. Further, a multi-DOF system model’s stiffness matrix and damping one construction method for three adjacent structures was presented and the multi-DOF system’s random response formulas were deduced based on the complex mode superposition method. Finally, the aseismic control effects of various combinations of the single-DOF system simplified model for three adjacent structures were analyzed, respectively and those of the multi-DOF system model for three adjacent structures were also studied in detail. The simulation results showed that after using connected damping devices, the aseismic control effects for three adjacent structures and those for two adjacent structures are almost the same; when the aseismic control is invalid due to two adjacent structures’ symmetry, the aseismic control effects for three adjacent structures are still better; in addition, three adjacent structures have a good robustness and their higher-order response peaks are suppressed significantly under random earthquake excitation.

adjacent structures; complex mode; symmetry; control; robustness

教育部创新团队项目(IRT13057)；国家自然科学基金(97315301-07;51478129)；广东省特支计划项目(2014TX01C141)

2016-04-20 修改稿收到日期：2016-06-14

刘良坤 男，博士生，1988年5月生

谭平 男，研究员，博士生导师，1973年9月生

TU352.1

A

10.13465/j.cnki.jvs.2017.15.002