不同种类气隙偏心故障对汽轮发电机转子不平衡磁拉力的影响
2017-08-30唐贵基邓玮琪何玉灵
唐贵基, 邓玮琪, 何玉灵
(华北电力大学 机械工程系,河北 保定 071003)
不同种类气隙偏心故障对汽轮发电机转子不平衡磁拉力的影响
唐贵基, 邓玮琪, 何玉灵
(华北电力大学 机械工程系,河北 保定 071003)
结合理论推导和数值仿真计算分析了径向气隙偏心对汽轮发电机转子径向不平衡磁拉力及其振动特性的影响。首先通过分析气隙静偏心、气隙动偏心以及气隙动静混合偏心情况下气隙磁场的变化,分别推导得到不同气隙偏心所引起的转子径向不平衡磁拉力表达式,并分析了转子的振动特征,然后利用电机有限元软件Ansoft Maxwell建立了实验室SDF-9型隐极故障模拟发电机的二维模型,计算得到了转子水平及竖直方向的径向不平衡磁拉力变化情况,并与理论分析和部分实验振动响应进行了对比,结果基本吻合。结果表明,气隙静偏心将产生二倍频不平衡磁拉力作用于转子上;气隙动偏心根据转子表面凹凸数量分为合外力为零及合外力不为零两种情况,当合外力不为零时,将产生一倍频不平衡磁拉力作用于转子;气隙动静混合偏心将同时产生一倍频和二倍频不平衡磁拉力作用于转子上(考虑动偏心时合外力不为零的情况)。同时随着偏心程度的增大,不平衡磁拉力也随之增大。
汽轮发电机;气隙偏心;不平衡磁拉力;振动特性
由于制造、装配和运行等多种原因,电机定转子间的气隙经常会存在一定程度的不均匀,造成气隙在一侧多,而在另一侧少的情况,此种现象称之为气隙偏心,例如导轴承偏移、定子铁芯变形等都会导致气隙偏心故障的产生。目前通常所说的气隙偏心大多是指径向偏心[1-6]。
气隙偏心根据偏心情况的不同,又可进一步分为静偏心,动偏心以及动静混合偏心。气隙静偏心是指定转子间最小气隙周向位置固定、不随转子旋转而发生变化的情况,例如定子铁芯变形,导轴承偏移等原因所引发的气隙偏心即属于此类情况;气隙动偏心是指定转子间径向气隙的最小位置会随着转子的旋转而发生改变,例如转子表面圆度不齐、转子挠度翘曲等原因所引起的气隙偏心即属于此类情况;气隙混合偏心是指既含有气隙静偏心又含有气隙动偏心的情况。
现有成果对于气隙偏心故障的研究主要集中在电动机和水轮发电机方面,对于汽轮发电机的报道则相对较少。在已有报道中,万书亭[7]研究了汽轮发电机气隙偏心故障时的气隙磁场,推导了气隙偏心故障下的定转子受到的不平衡磁拉力公式,得到了气隙偏心故障时定转子的振动特性;万书亭等[8]详细计算了各脉振频率上的径向电磁力,利用SDF-9型故障模拟发电机实测了静偏心时振动信号,验证了气隙静偏心将引起定转子的二倍频振动;何玉灵等[9]采用通频烈度比对与特定频率成分幅值比对的计算方法鉴定出发电机的偏心故障程度,同样进行了静偏心的故障实验。
以上研究成果多限于定性的理论推导与验证,缺乏定量的数值仿真计算,涉及动偏心的部分仅考虑转子表面一处凹凸的情况,在一般性和通用性上可进一步改进。本文将考虑多种偏心故障作用下的磁拉力表达式。此外,以上文献的故障实验均没有涉及动偏心或动静混合偏心故障,原因是实际发电机要改变转子外形是不容易的,本文将以汽轮发电机为研究对象,利用Ansoft仿真软件建立二维静偏心、动偏心和动静混合偏心故障模型,分析因转子表面圆度形变产生的气隙动偏心,以及动静混合偏心对发电机转子径向不平衡磁拉力的影响。
1 偏心故障前后转子振动特性分析
1.1 偏心故障下的气隙磁密
由万书亭研究结论可知汽轮发电机在正常运行时的气隙磁势可表示为
(1)
式中:Fr为主磁势;Fs为电枢反应磁势;ωr=2πfr为转子机械角频率;fr为转子的机械频率;α为定子机械角度;ψ为发电机内功角。
(2)
同时考虑气隙静偏心及动偏心,选择如图1所示的坐标系,以定转子静偏心时最小气隙处为原点(若不存在静偏心,则以x轴正向为原点),则气隙为:
(3)
式中:g为平均气隙;δs为相对静偏心;δdn为相对动偏心(动偏心使气隙减小为δdn;增大为-δdn);n为动偏心数量;θn为零初始时刻第n个动偏心距离原点的角度。

(a) 正常情况

(b) 静偏心

(c) 动偏心n=2

(d)静偏心+动偏心n=1
由于气隙偏心很小,气隙磁导由幂级数展开为(忽略高阶分量):
(4)
式中:Λ0为气隙磁导的常值分量;Λs=Λ0δs为静偏心引起的磁导分量;Λdn=Λ0δdn为动偏心引起的磁导分量。
1.2 单位面积磁拉力
先通过气隙磁势和磁导,求得气隙磁密
B(α,t)=Λ(α,t)f(α,t)
(5)
然后利用式(6)求得转子表面单位面积径向磁拉力(其中:μ0为空气磁导率)

(6)
(7)
1.3 不同气隙偏心下的转子磁拉力
由万书亭的研究可知,转子不平衡磁拉力可以由式(8)计算。
将不同偏心时的气隙条件:静偏心(δs≠0,δdn=0)、动偏心(δs=0,δdn≠0),以及动静混合偏心(δs≠0,δdn≠0)分别代入式(7),并且联立式(8),可以求得静偏心、动偏心以及动静混合偏心情况下的转子所受不平衡磁拉力分别如式(9)~(11)所示。
(8)
(9)
(10)
(11)
根据激励与响应同频的关系,对于汽轮发电机转子,它的振动特征频率与其所受到的不平衡磁拉力激励频率相同。
式(9)为静偏心情况下转子受到的不平衡磁拉力,式中含有直流分量和二倍频分量。其中直流分量不引起转子振动,而是产生一个恒定的常力作用在转子上,该常力的长期作用会使转子产生变形的趋势;而式中的二倍频分量是一个脉振力,该脉振力将会引发转子产生与其同频的径向振动,即二倍频振动。此外,从式中还可以看到,随着Λs的增大,转子所受到的不平衡磁拉力的幅值也相应增大。
式(10)为动偏心情况下转子受到的不平衡磁拉力,式中仅含有一倍频分量,该一倍频脉振力激励将会引起转子一倍频的振动响应。同时,动偏心故障激发转子的振动还与动偏心数量n、各动偏心故障程度Λdn和各动偏心与原点的夹角θn有关。因此,当合力为零,不激发振动;合力不为零,则激发转子一倍机械频率的振动,且随着Λdn的增大,转子所受到的不平衡磁拉力的幅值也应增大。
式(11)为动静混合偏心情况下转子受到的不平衡磁拉力,式中含有直流分量、一倍频分量和二倍频分量,它将会同时激发转子一倍频、二倍频的振动(考虑动偏心时合力不为零的情况),且随着Λs和Λdn的增大,转子所受到的不平衡磁拉力的幅值也相应增大。
2 验证与分析
2.1 验证方法及设置
验证基于华北电力大学电机实验室的SDF-9型隐极故障模拟发电机进行,如图2(a)所示,对应的参数如表1所示。因条件限制此电机只能实现静偏心故障的模拟,无法实现对因转子变形引起的气隙动偏心故障的模拟,本文采用真机实验和计算机仿真结合来验证静偏心理论分析,动偏心和混合偏心部分仅采用数值仿真计算的方法进行验证。

表1 SDF-9 型隐极故障模拟发电机基本参数
故障模拟发电机对静偏心故障的模拟方法为:转子通过落地式轴承支座固定在底架上保持不动,定子可相对转子作一定的水平径向位移,在电机正面和背面均有两枚调节螺栓,通过拧动正面和背面的两枚调节螺栓来实现定子的前、后移动操作,移动量则通过两个百分表来控制,从而模拟静偏心故障,如图2(b)所示。

(a) 总体外观


(b) 静偏心设置方法
仿真采用电机有限元软件Ansoft Maxwell 15.0进行,所建立的电机二维模型如图3(a)所示。为了建模方便,仿真实验模拟的动偏心故障是转子的内凹故障,即动偏心取-δdn。仿真过程中,设置发电机励磁电流为0.4 A,转速为3 000 r/min,分别计算表2中各偏心条件下的径向不平衡磁拉力和振动特性。故障的动偏心模拟方法是用一个与转子等大的圆柱体去与转子进行布尔运算,实现转子的内凹故障。详细步骤如图3(b)所示:O1为转子中心,O2为圆柱体中心,从两圆柱体相切位置开始,分别对两圆柱体圆心线O1O2减少Δ=0.1 mm,0.2 mm和0.3 mm(对应相对动偏心程度δd=12.5%,25%和37.5%)时的模型进行布尔subtract运算,保留转子部分,最后进行转子的不平衡磁拉力仿真分析。

(a)

(b)

静偏心动偏心混合偏心条件1δs=12.5%n=2θ1=0°θ2=90°δd1=δd2=12.5%n=2θ1=0°θ2=180°δd1=δd2=12.5%n=1θ1=0°δs=12.5%δd1=12.5%n=1θ1=0°δs=12.5%δd1=12.5%条件2δs=25%n=2θ1=0°θ2=90°δd1=δd2=25%n=2θ1=0°θ2=180°δd1=δd2=25%n=1θ1=0°δs=25%δd1=12.5%n=1θ1=0°δs=12.5%δd1=25%条件3δs=37.5%n=2θ1=0°θ2=90°δd1=δd2=37.5%n=2θ1=0°θ2=180°δd1=δd2=37.5%n=1θ1=0°δs=37.5%δd1=12.5%n=1θ1=0°δs=12.5%δd1=37.5%
2.2 结果分析与讨论
2.2.1 静偏心对转子受力及振动特性的影响
(1) 仿真结果
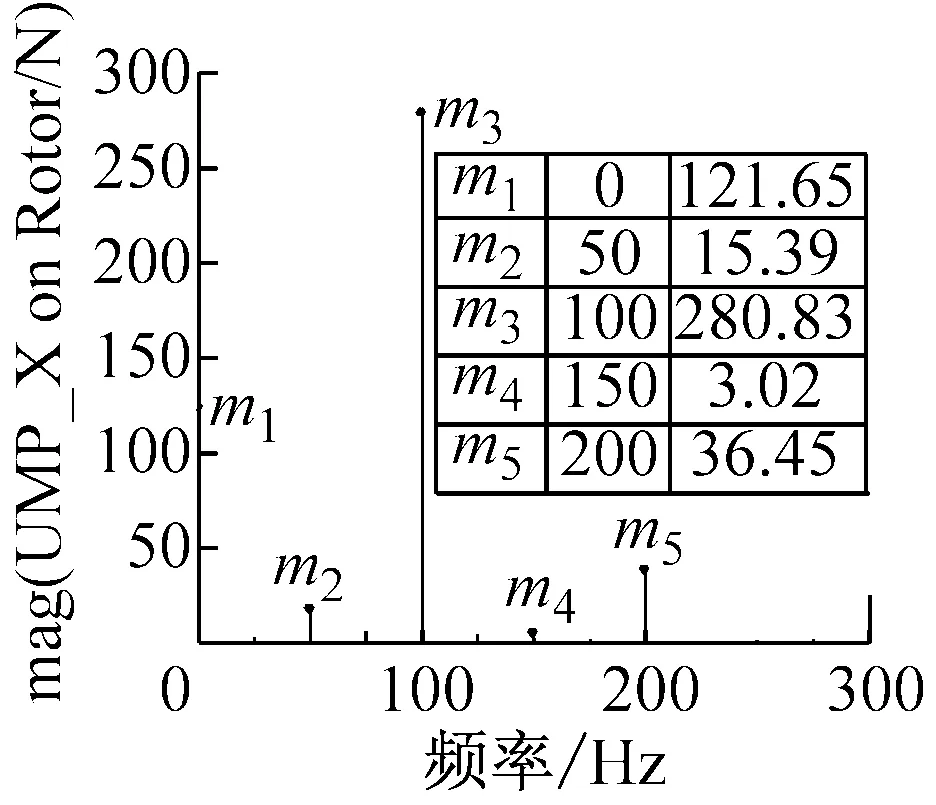
图4为不同静偏心仿真情况下的转子x方向受力图,从图中可以看出,正常情况下转子所受合力几乎为零,当转子发生静偏心故障后,转子x方向受力开始增大,且随着偏心程度的加剧,转子所受x方向的不平衡磁拉力的峰值也随之增大。
从图5(a)中可以看出正常情况下转子x方向的受力频谱各频率成分都较小,基本在同一数量级上;从图5(b)中可以看出,当转子发生静偏心故障时,二倍频分量增大较为突出,其他频率成分有增有减;从图5(c)、(d)中可以看出,随着静偏心量的增大,直流分量和二倍频分量幅值逐渐增大,其他频率成分变化情况较小,结果与理论相符。

图4 不同静偏心仿真情况下转子x方向受力图
(2) 实验结果
图6为不同静偏心实验情况下的转子振动频谱图,理论上,正常运行情况下,发电机转子应无振动,但图6(a)中显示发电机在正常运行情况下转子存在多种频率成分的振动,这是由于电机内部的不对称和外部非故障环境因素影响所造成的。由图6(a)、(b)、(c)可看出,与正常情况相比,发电机在气隙静偏心故障下转子二倍频振动有极为明显的变化,而其它频率成分的振动幅值则变化较小,反映了发电机在气隙静偏心故障下转子将产生二倍频振动;图中显示二倍频振动幅值随着偏心程度的加剧而增大,这与前面的理论分析结果相吻合。
此外,图7还给出了100 Hz时,仿真下转子不平衡磁拉力的幅值曲线和实验下转子振动速度的幅值曲线。通过对比可知,随着静偏心的增大,转子二倍频振动加剧,这与转子所受磁拉力的二倍频成分的增长趋势相一致。

(a) 正常情况

(b) 静偏心12.5%
(c) 静偏心25%

(d) 静偏心37.5%

(a) 正常运行

(b) 0.1 mm气隙静偏心

(c) 0.3 mm气隙静偏心

(a) 仿真下转子磁拉力二倍频幅值

(b) 实验下转子振动速度二倍频幅值
2.2.2 动偏心对转子不平衡磁拉力的影响
动偏心和动静混合偏心故障均在转子内凹故障下讨论,即动偏心取-δdn。
为了验证不平衡磁拉力受到动偏心、偏心角度的影响,这里分别考虑n=2,δd1=δd2=δd,θ2-θ1=90°和n=2,δd1=δd2=δd,θ2-θ1=180°两种动偏心故障情况。根据式(10)可得两种动偏心故障下的x方向不平衡磁拉力F1和F2:
(12)
即,当两相同程度的动偏心故障呈90°时,将引起转子x方向一倍频振动;而当两相同程度的动偏心故障呈180°时,转子x方向合力为零。
图8(a)为n=2,δd1=δd2=δd,θ2-θ1=90°不同动偏心情况下的转子x方向受力图,从图中可以看出,正常情况下转子所受合力几乎为零,当转子发生动偏心故障后,转子x方向受力开始增大,且随着偏心程度的加剧,转子所受x方向的不平衡磁拉力的峰值也随之增大。
从图9(a)中可以看出正常情况下转子x方向的受力频谱各频率成分都较小,基本在同一数量级上;从图9(b)中可以看出,当转子发生动偏心故障后,一倍频分量增大较为突出;从图9(c)、(d)中可以看出,随着动偏心量的增大,一倍频分量幅值逐渐增大,其他频率成分变化情况较小。
图8(b)为n=2,δd1=δd2=δd,θ2-θ1=180°不同动偏心情况下的转子x方向受力图,图中曲线相互重叠,不易分辨,可通过表3中各曲线的平均值进行分析。
表3n=2,δd1=δd2=δd,θ2-θ1=180°时转子x向受力均值
Tab.3 Rotor UMP mean value undern=2,δd1=δd2=δd,θ2-θ1=180° dynamic eccentricity fault

正常δd1=12.5%δd2=12.5%δd1=25%δd2=25%δd1=37.5%δd2=37.5%1.1900N-0.2252N0.0443N1.1469N
从表3可以看出,正常情况和各动偏心情况下转子x方向所受的不平衡磁拉力平均值并不为零,但是一个接近于零的数,这是由于计算机的计算误差导致的,而且图8(a)与图8(b)相差很大的数量级,故可以认为n=2,δd1=δd2=δd,θ2-θ1=180°不同动偏心情况下的转子x方向受力为零,与理论结果相符合。

(a) n=2,δd1=δd2=δd,θ2-θ1=90°动偏心情况

(b) n=2,δd1=δd2=δd,θ2-θ1=180°动偏心情况
Fig.8 Rotor UMP under normal condition and dynamic eccentricity fault
从图10中也可以看出动偏心情况下转子x方向的受力频谱与正常情况下转子x方向的受力频谱,相比之下基本不变。
2.2.3 混合偏心对转子不平衡磁拉力的影响
混合偏心的条件为:静偏心和n=1,δd1=δd,θ1=0°动偏心混合的情况。根据式(11)则有:
(13)

(a) 正常情况

(b) 动偏心12.5%

(c) 动偏心25%

(d) 动偏心37.5%

(a) 正常情况

(b) 动偏心12.5%

(c) 动偏心25%

(d) 动偏心37.5%
即,混合偏心将会同时激发转子一倍频、二倍频的振动,且随着Λs和Λd的增大,转子所受到的不平衡磁拉力的幅值也应增大。
图11(a)为静偏心(12.5%、25%、37.5%)和动偏心(n=1;θ1=0°;12.5%)混合偏心情况下转子x方向受力图,图中曲线相互重叠,不易分辨,我们可以通过表4中各条曲线的平均值进行分析。


图11 不同动静混合偏心情况下转子x方向受力图

(a) 动偏心12.5%

(b) 静偏心12.5%+动偏心12.5%

(c) 静偏心25%+动偏心12.5%

(d) 静偏心37.5%+动偏心12.5%
图12 静偏心(12.5%、25%、37.5%)和动偏心(n=1;12.5%)混合情况下转子x方向受力频谱
Fig.12 Rotor vibration spectrum under mixed eccentricity fault
从表4可以看出,只受动偏心单故障情况时转子x方向所受的不平衡磁拉力平均值较小;当转子发生混合偏心故障后,转子x方向受力开始增大,且随着混合偏心中静偏心程度的加剧,转子所受x方向的不平衡磁拉力的平均值也随之增大。
从图12(a)中可以看出转子只受动偏心作用时转子x方向的受力频谱存在很大的一倍频分量;从图12(b)中可以看出,当转子发生混合故障后,二倍频分量增大较为突出,其他频率成分有增有减;从图12(c)、(d)中可以看出,随着混合偏心量的增大,二倍频分量幅值逐渐增大,其他频率成分变化情况较小。
图11(b)静偏心(12.5%)和动偏心(n=1;θ1=0°; 12.5%、25%、37.5%)情况下转子x方向受力图,从图中可以看出,转子只受静偏心作用时所受合力较小,当转子发生混合偏心故障后,转子x方向受力开始增大,且随着偏心程度的加剧,转子所受x方向的不平衡磁拉力的峰值也随之增大。
从图13(a)中可以看出转子只受静偏心作用时转子x方向的受力频谱存在较大的二倍频分量;从图13(b)中可以看出,当转子发生混合偏心故障后,一倍频分量开始明显增加;从图13(c)、(d)中可以看出,随着动偏心量的增大,一倍频分量幅值逐渐增大,其他频率成分变化情况较小。

(b) 静偏心12.5%+动偏心12.5%

(c) 静偏心12.5%+动偏心25%

(d) 静偏心12.5%+动偏心37.5%
图13 静偏心(12.5%)和动偏心(n=1;12.5%、25%、37.5%)混合情况下转子x方向受力频谱
Fig.13 Rotor vibration spectrum under mixed eccentricity fault
3 结 论
本文通过理论推导和二维有限元建模仿真及实验,得到以下几点结论:
(1) 静偏心单故障将会引起转子二倍机械频率的振动,且随着静偏心故障程度的增大,转子所受的不平衡磁拉力也变大;
(2) 动偏心故障激发转子的振动与动偏心数量n、各动偏心故障程度Λdn和各动偏心与原点的夹角θn有关。合力为零,不激发振动;合力不为零,则激发转子一倍频率的振动,且随着Λdn的增大,转子所受到的不平衡磁拉力的幅值也应增大;
(3) 混合偏心故障可以看作是静偏心和动偏心故障的叠加,它将会同时激发转子一倍频、二倍频的振动(考虑动偏心时合力不为零的情况),且随着Λs和Λdn的增大,转子所受到的不平衡磁拉力的幅值也应增大。
以上结论可以为发电机故障诊断提供依据。
[1] DORREL D G. Experimental behaviour of unbalanced magnetic pull in 3-Phase induction motors with eccentric rotors and the relationship with tooth saturation[J]. IEEE Transactions on Energy Conversion, 1999, 14(3): 304-309.
[2] LI Weili, TANG Li, ZHANG Xiaocheng, et al. Calculation and analysis of high-speed permanent magnetic generator unilateral magnetic force[J]. Electrical Machines and Systems, 2008, 17(20): 3284-3288.
[3] WANG L, RICHARD W C, MA Z Y, et al. Finite-element analysis of unbalanced magnetic pull in a large hydro-generator under practical operations[J]. IEEE Transactions on Magnetics, 2008, 44(6): 1558-1561.
[4] 赵向阳, 葛文韬. 基于定子电流法监测无刷直流电动机转子动态偏心的故障模型仿真研究[J]. 中国电机工程学报, 2011, 31(36): 124-130.
ZHAO Xiangyang, GE Wentao. Simulation research of fault model of detecting rotor dynamic eccentricity in brushless DC motor based on motor current signature analysis[J]. Proceedings of the CSEE, 2011, 31(36):124-130.
[5] 诸嘉慧,邱阿瑞,陶果.转子偏心及定子斜槽凸极同步发电机支路的感应电动势[J]. 清华大学学报(自然科学版),2008,48(4): 453-456.
ZHU Jiahui, QIU Arui, TAO Guo. Branch voltage of a salient pole synchronous generator with eccentric rotor and skewed slots[J]. Journal of Tsinghua University(Science and Technology), 2008, 48(4): 453-456.
[6] 万书亭,何玉灵,唐贵基.发电机气隙偏心时定子并联支路的环流特性分析[J]. 高电压技术,2010,36(6):1547-1553.
WAN Shuting, HE Yuling, TANG Guiji. Analysis on stator circulating current characteristics under eccentricity faults of turbo-generator[J]. High Voltage Engineering, 2010,36(6): 1547-1553.
[7] 万书亭. 发电机绕组与偏心故障交叉特征分析及其检测方法研究[D]. 保定: 华北电力大学, 2005.
[8] 万书亭,李和明,李永刚. 气隙偏心对汽轮发电机定转子振动特性的影响[J]. 振动与冲击,2005, 24(6): 21-23.
WAN Shuting, LI Heming, LI Yonggang. Analysis on vibration characteristics of generator with the fault of eccentric air-gap[J]. Journal Of Vibration and Shock, 2005, 24(6): 21-23.
[9] 何玉灵,万书亭,唐贵基,等.基于定子振动特性的汽轮发电机气隙偏心故障程度鉴定方法研究[J]. 振动与冲击,2012, 31(22):53-57.
HE Yuling, WAN Shuting, TANG Guiji, et al. Eccentric fault level identification of a turbo-generator based on stator vibration characteristics[J]. Journal of Vibration and Shock, 2012, 31(22):53-57.
Effect of different kinds of air-gap eccentricity faults on rotor UMP of a turbo-generator
TANG Guiji, DENG Weiqi, HE Yuling
(Department of Mechanical Engineering, North China Electric Power University, Baoding 071003, China)
Here, theoretical derivation and numerical simulation were used to analyze the effects of radial air-gap eccentricity on unbalanced magnetic pull (UMP) of a turbo-generator’s rotor and the rotor vibration characteristics. Firstly, the variation laws of air-gap magnetic field under static air-gap eccentricity, dynamic one and mixed one were analyzed. Then the rotor UMP formulas due to different air-gap eccentricity faults were deduced and the rotor vibration characteristics were analyzed. Finally, the SDF-9 type non-salient pole synchronous generator model was built with the software Ansoft Maxwell to calculate the detailed UMP data for comparing with those of theoretical analysis and parts of tests. All results of theoretical analysis, numerical simulation and tests agreed well with each other. It was shown that the static air-gap eccentricity causes a rotor UMP with a frequency of 2f(fis the rotor rotating frequency); however, there are two cases including the resultant force of zero and not zero for the dynamic air-gap eccentricity, during the latter the rotor UMP with a frequency of f is caused; in the case of mixed air-gap eccentricity, the rotor UMPs with frequencies offand 2f, respectively are caused during the resultant force of not zero; with increase in the air-gap eccentricity, the rotor UMP increases.
turbo-generator; air-gap eccentricity; unbalanced magnetic pull (UMP); vibration characteristics
国家自然科学基金(51307058);河北省自然科学基金(E2014502052;E2015502013);中央高校基本科研业务费专项基金重点项目(2015ZD27)
2015-12-09 修改稿收到日期:2016-06-19
唐贵基 男,博士,教授,博士生导师,1962年生
TM31;O323
A
10.13465/j.cnki.jvs.2017.15.001
