两级渐开线齿轮传动系统横-摆-扭耦合非线性动力学建模与试验验证
2017-08-30刘辉,张晨,王成
刘 辉, 张 晨, 王 成
(1. 北京理工大学 机械与车辆工程学院,北京 100081;2. 中国北方车辆研究所,北京 100072)
两级渐开线齿轮传动系统横-摆-扭耦合非线性动力学建模与试验验证
刘 辉1, 张 晨1, 王 成2
(1. 北京理工大学 机械与车辆工程学院,北京 100081;2. 中国北方车辆研究所,北京 100072)
以两级渐开线齿轮传动系统为研究对象,分析了几何偏心、中心距安装误差以及齿轮中心支撑弯曲变形引起中心距的变化对啮合角和间隙的影响,引入非线性动态啮合刚度模型,得到了各级齿轮传动的非线性动态啮合力。采用拉格朗日方法建立了考虑偏心、间隙、时变啮合角以及非线性动态啮合刚度模型的两级齿轮传统系统横-摆-扭非线性动力学模型,采用4阶定步长龙哥库塔法求解非线性动力方程。针对一个两级齿轮传统系统试验装置进行理论计算和试验测试,安装在齿轮圆周对称位置的角加速度传感器,测试结果显示各工况下齿轮角加速度仿真值与实验值最大误差为23.51%;固定安装在箱体上的位移传感器测得振动位移仿真值与实验值最大误差为21.21%;粘贴在轴上的应变片测得扭转切应力仿真值与实验值最大误差为17.9%。研究结果表明:仿真结果与试验结果的变化趋势基本吻合,且误差在可接受范围内。分析了可能导致仿真结果与试验结果之间产生误差的原因,验证了渐开线直齿轮传动横-扭-摆耦合非线性动力学模型和非线性动态啮合模型的正确性。
齿轮;非线性;试验验证;间隙;啮合角
齿轮传动系统是应用最为广泛的机械传动系统形式之一,随着齿轮传动系统向着高速、重载方向发展,在内、外激励共同作用下齿轮传动系统产生的振动和噪声,严重影响其使用性能。建立精确的动力学模型研究齿轮传动系统的动态性能已成为了重要的研究课题[1]。国内、外学者对齿轮传动非线性动力学模型以及齿轮动态特性做了广泛和深入的研究。
齿轮传动系统的动力学模型经历了由线性到非线性,由定常到时变的发展过程[2],间隙和时变刚度也成为了重要的非线性因素。在齿轮非线性动力学模型中,间隙多为定值,时变刚度采用准静态的方法获得,两者作为齿轮非线性动力学方程的输入条件。Kahraman等[3]考虑定常间隙和周期刚度的时变性,建立了三自由度齿轮非线性动力学模型,研究了时变刚度与间隙之间的耦合作用。Lassaad等[4]建立了两级齿轮传动非线性动力学模型,模型中考虑定常间隙和周期时变刚度。崔亚辉等[5]考虑定常间隙、时变周期刚度,建立了齿轮—转子耦合系统,并研究了动态响应及齿侧间隙对振幅跳跃特性的影响。近期,Skrickij等[6]对啮合刚度的计算方法进行了研究,考虑中心距偏差对啮合刚度的影响,在此基础上研究了齿轮的非线性动力学特性。Kim等[7]考虑了齿面、齿背啮合相位差造成非对称啮合刚度模型,分析了齿轮传动系统的空载敲击特性。Chen等[8]忽略间隙,考虑中心弯曲变形对啮合角的影响并采用矩形波形式的啮合刚度,建立了齿轮6自由度非线性动力学模型,并研究了系统参数对此轮动态特性的影响。Chen等[9]考虑了中心距变化对间隙的影响,研究了动态间隙对齿轮动态特性的影响。Zhang等[10]考虑了几何偏心的影响,建立了齿轮非线性动力学模型,研究了几何偏心对齿轮动态特性的影响。
齿轮传动过程中,齿轮的间隙和时变刚度与齿轮的实际运动状态密切相关。为了能够更加准确的描述齿轮传动过程中的啮合状态,需要建立与齿轮实际运动状态密切相关的齿轮非线性动态啮合模型。本文基于渐开线齿轮的啮合原理,首先,考虑几何偏心、中心距偏差分析了齿轮中心距变化对啮合角和间隙的影响,随后,分析了齿轮的转速波动、齿轮中心距变化以及齿面、齿背啮合相位差对啮合点的影响,结合单、双齿啮合边界条件并采用解析法计算啮合刚度,最后,提出了齿轮传动的非线性动态啮合反馈模型。考虑几何偏心、陀螺力矩、啮合偏载力矩和非线性动态啮合反馈模型,建立了10自由度单级齿轮传动非线性动力学模型,并采用数值法求解非线性动力学方程。对比研究了不同模型下齿轮动态特性随转速的变化趋势,最后,研究了中心距偏差对齿轮动态特性的影响。针对一个两级齿轮传统系统试验装置进行理论计算和试验测试,通过安装在箱内的传感器分别采集了各工况下齿轮的角加速度、振动位移以及轴的扭转切应力值。对比分析了各仿真结果与试验结果的变化趋势,且误差在可接受范围内。最后分析了可能导致仿真结果与试验结果之间产生误差的原因。
1 齿轮传动非线性动态啮合力
两级齿轮传动系统三维动力学模型如图1所示,绝对坐标系OXY中心位于齿轮1旋转中心位置,Ci、为齿轮i的质心位置,ei为齿轮i的几何偏心。齿轮轮体简化为刚体,每个齿轮存在5个自由度,包含两个平移自由度x,y以及三个扭转自由度θx,θy,θz。zi为齿轮i的齿数,rbi为齿轮i的基圆半径,mi为齿轮i的质量,Ixi,Iyi,Izi为齿轮i的转动惯量,i=1,2,3,4。
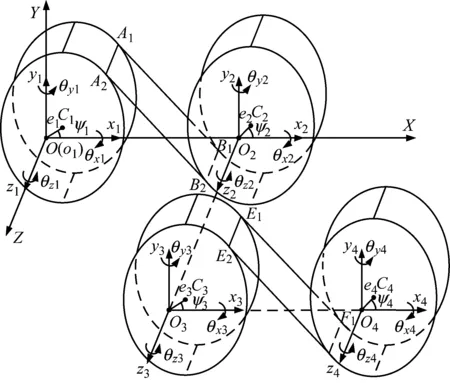
图1 两级齿轮传动三维动力学模型
齿轮1和齿轮2作用力始终沿着啮合面方向A1A2-B1B2,齿轮2和齿轮3作用力始终沿着啮合面方向E1E2-F1F2。各级齿轮副间通过沿啮合面方向上的平面力系相互作用,如图2所示。由于齿向误差以及轴或轴承变形引起啮合偏差,轮此间的相互作用为沿齿宽方向为非均布载荷,该平面力系可简化为合力Fm和垂直于啮合面上的偏摆扭矩T,其中,Fm采用非线性动态啮合反馈模型计算,定义啮合力的偏置距τ,可得偏摆扭矩T两级齿轮传动动力学模型在Z轴上的二维投影模型如图3所示,图中,α12和α34分别为齿轮副的啮合角,γ12和γ34分别为齿轮副的位置角,φ为齿轮3相对于坐标系OXY的初始位置角。虚线为初始时刻齿轮的相对位置,实线为任意时刻齿轮的相对位置。
T=Fmτ
(1)
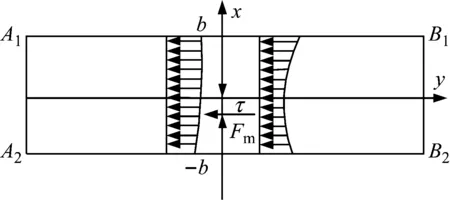
图2 外啮合齿轮副平面力系示意图
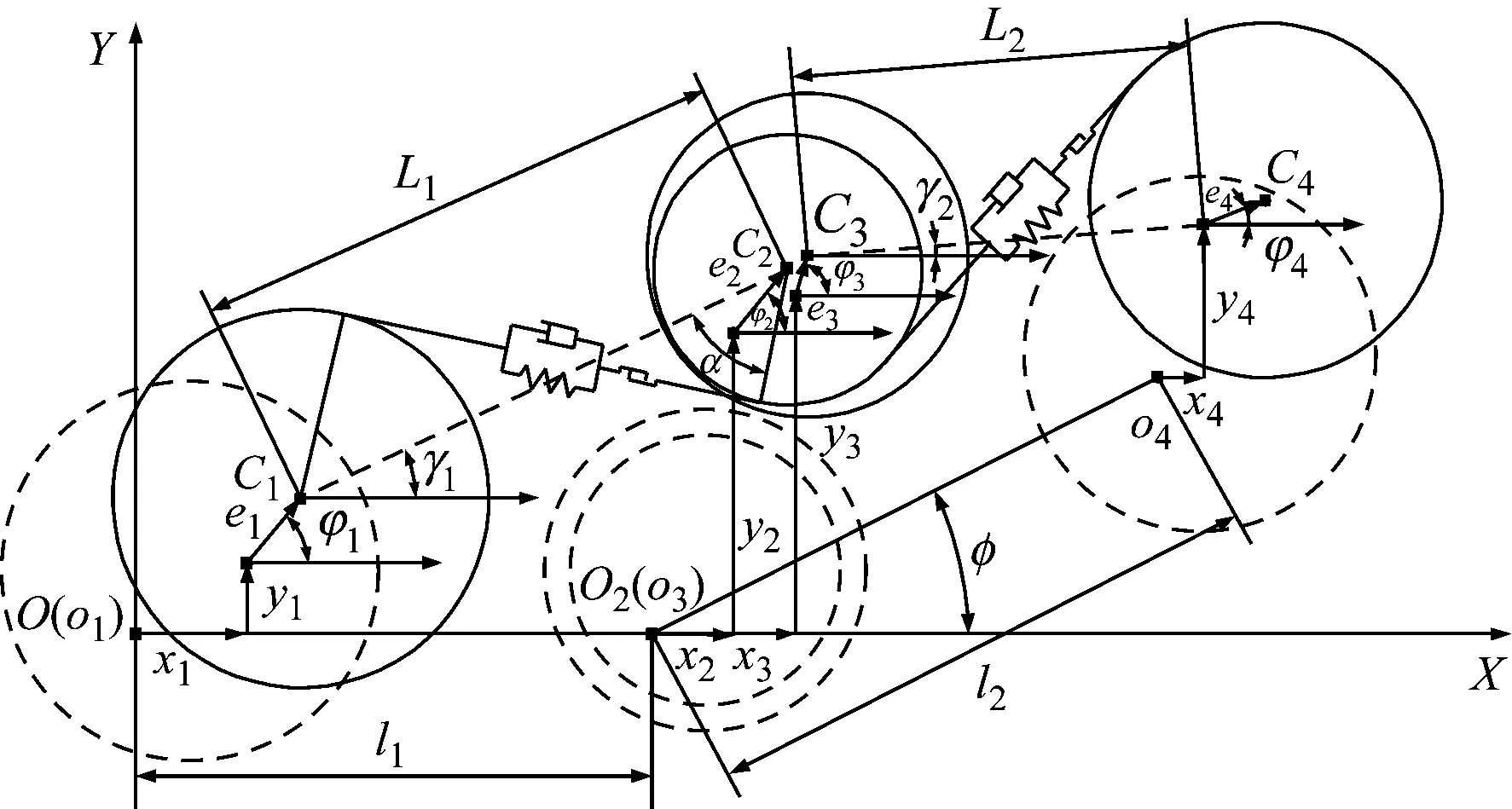
图3 两级齿轮传动系统Z轴二维投影模型
由图可知,任意时刻齿轮1、齿轮2和齿轮3的质心位置矢量R1、R2、R3和R4分别为:
R1=(x1+e1cos(φ1))i+(y1+e1sin(φ2))j
(2)
R2=(x2+e2cos(φ2)+l1)i+(y2+e2sin(φ2))j
(3)
R3=(x3+e3cos(φ3)+l1)i+(y3+e3sin(φ3))j
(4)
R4=(x4+e4cos(φ4)+l1+l2cos(φ))i+
(y4+e4sin(φ4)+l2sin(φ))j
(5)
式中:i,j分别为绝对坐标系X,Y坐标上的单位矢量;φ1,φ2,φ3和φ4分别为齿轮1、齿轮2、齿轮3和齿轮4的转角。
令
Δx1=x2-x1+e2cos(φ2)-e1cos(φ1)
(6)
Δy1=y2-y1+e2sin(φ2)-e1sin(φ1)
(7)
Δx2=x4-x3+e4cos(φ4)-e3cos(φ3)
(8)
Δy2=y4-y3+e4sin(φ4)-e3sin(φ3)
(9)
可得,任意时刻各级齿轮传动的中心距L1,L2
(10)
(11)
式中,l1、l2分别为齿轮传动初始安装中心距,表示为

(12)
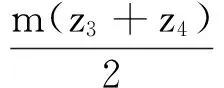
(13)
式中,ea1和ea2分别为各级齿轮传动的中心距偏差。
由几何关系可得各级齿轮传动动态啮合角α1和α2
(14)
(15)
各级齿轮传动任意时刻位置角γ1和γ2
(16)
(17)
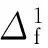
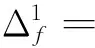


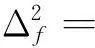
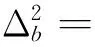

(18)
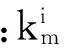
bi=bti+Δbi
(19)
式中:bti齿厚消减形成的齿侧间隙;Δbi为中心距变化引起的齿侧间隙变化。由几何关系可得,中心距变化引起的齿侧间隙变化量

(20)

(21)

f(b,Δ1,Δ2)为啮合线变化量,f1(b,Δ1,Δ2)为啮合线变化量的速度函数,表达式分别为
(22)
(23)


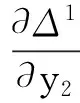
(24)


(25)
2 齿轮传动系统非线性动力学方程
两级齿轮传动的动能函数、势能函数、耗能函数分别为
(26)

(27)

(28)
式中,z=[q1,q2,q3,q4]T,z=[q1,q2,q3,q4]T,i=1,2,3,4,Ki,Ci分别为齿轮中心支撑刚度和阻尼矩阵,其中阻尼矩阵采用瑞利比例阻尼。
将动能、势能、耗能函数代入到拉格朗日函数
(29)
式中,Qi为非线性啮合力、力矩和外激励组成的广义力列向量。
由于在不同啮合线上啮合力的方向发生变化,对各级齿轮副分别定义角度φ和分段函数g
(30)
(31)
(32)
(33)
考虑陀螺力矩的影响,可得两级齿轮传动系统的非线性动力学方程。
齿轮1的动力学方程为:
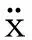

(34)
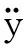
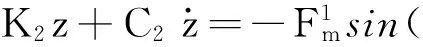
(35)

(36)
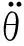
(37)

(38)
齿轮2的动力学方程为:
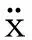
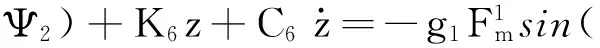
(39)
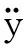
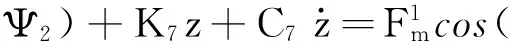
(40)
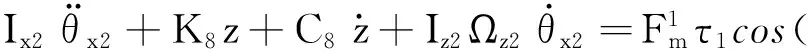
(41)
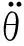
(42)
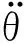

(43)
齿轮3的动力学方程为:
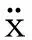
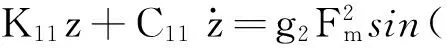
(44)
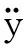
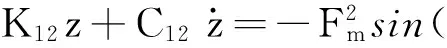
(45)
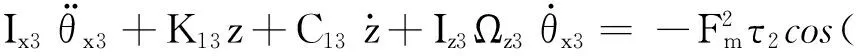
(46)

(47)
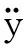
(48)
齿轮4的动力学方程为:
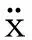
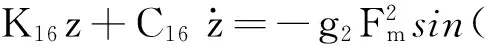
(49)
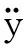
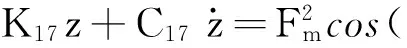
(50)

(51)
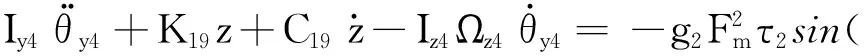
(52)
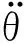

(53)
式中,Kj代表支撑刚度矩阵的第j行,j=1,2,…,20。
齿轮传动系统横-扭-摆耦合非线性动力学方程与齿轮啮合动态反馈模型仿真流程,如图4所示。
3 齿轮传动系统数值仿真与试验验证
针对所示两级齿轮传动试验装置分别进行数值仿真和试验测试,各级齿轮副参数如表1和表2所示。
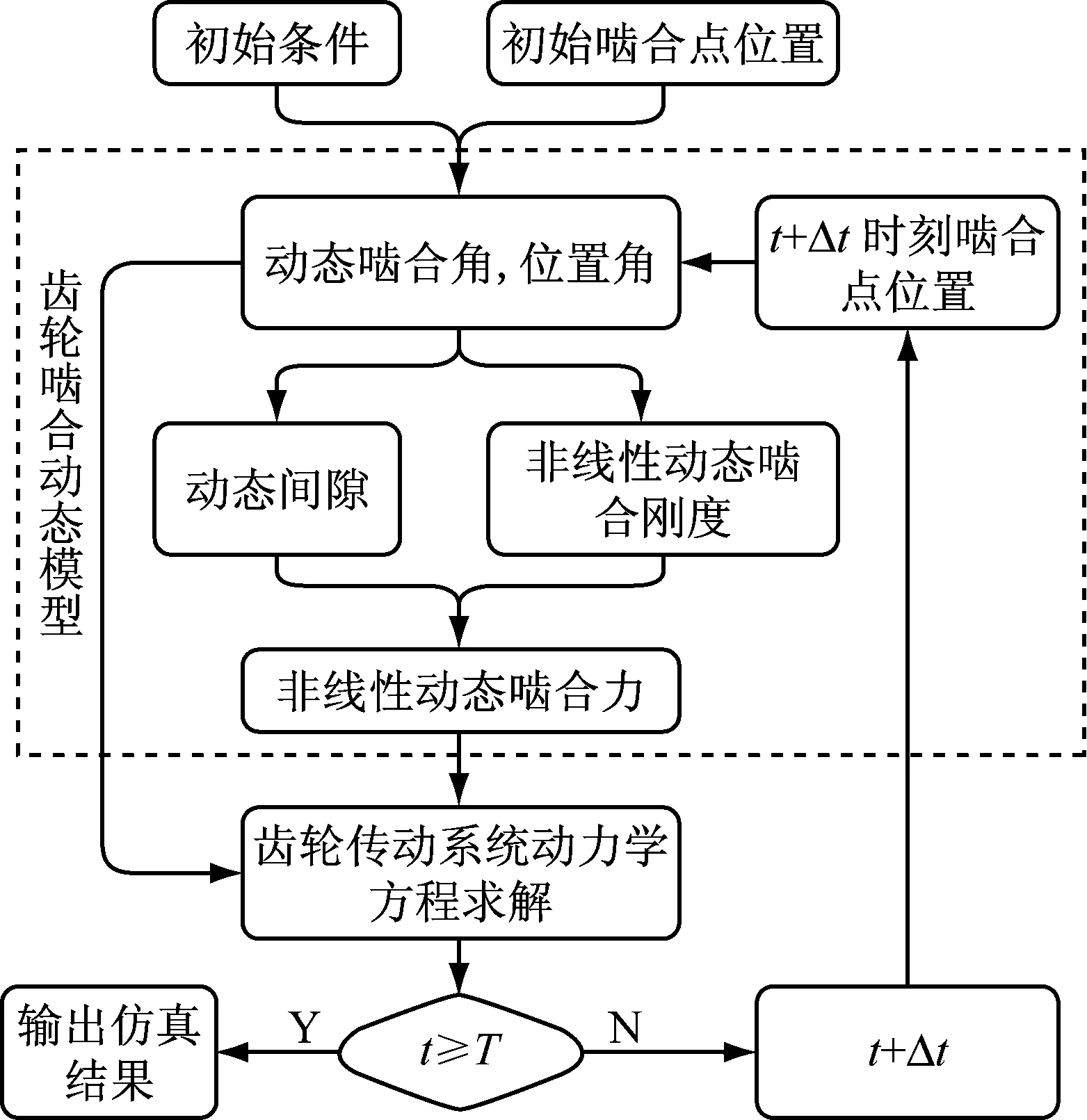
图4 反馈计算流程

参数数值齿数z1=93,z2=58模数/mm3间隙/mm0.3理论压力角/(°)20中心距偏差/mm0.05几何偏心/mme1=0.02,e2=0.02

表2 第2级齿轮副参数
3.1 两级齿轮传动试验装置与测试方法
两级齿轮传动试验台布置示意图及实物图分别如图5和图6所示。
利用泵马达加载试验装置,为了测试旋转部件的应力和加速度等信号实现从旋转位置到固定位置传送信号,必须通过集流环或采用近程遥测装置,本实验在轴端安装了集流环将旋转测试信号引入到数据采集前端。


图5 两级齿轮传动试验台布置示意图

图6 两级齿轮传动试验台实物图

(54)
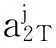
(55)

(56)
加速度均方根值定义为
(57)
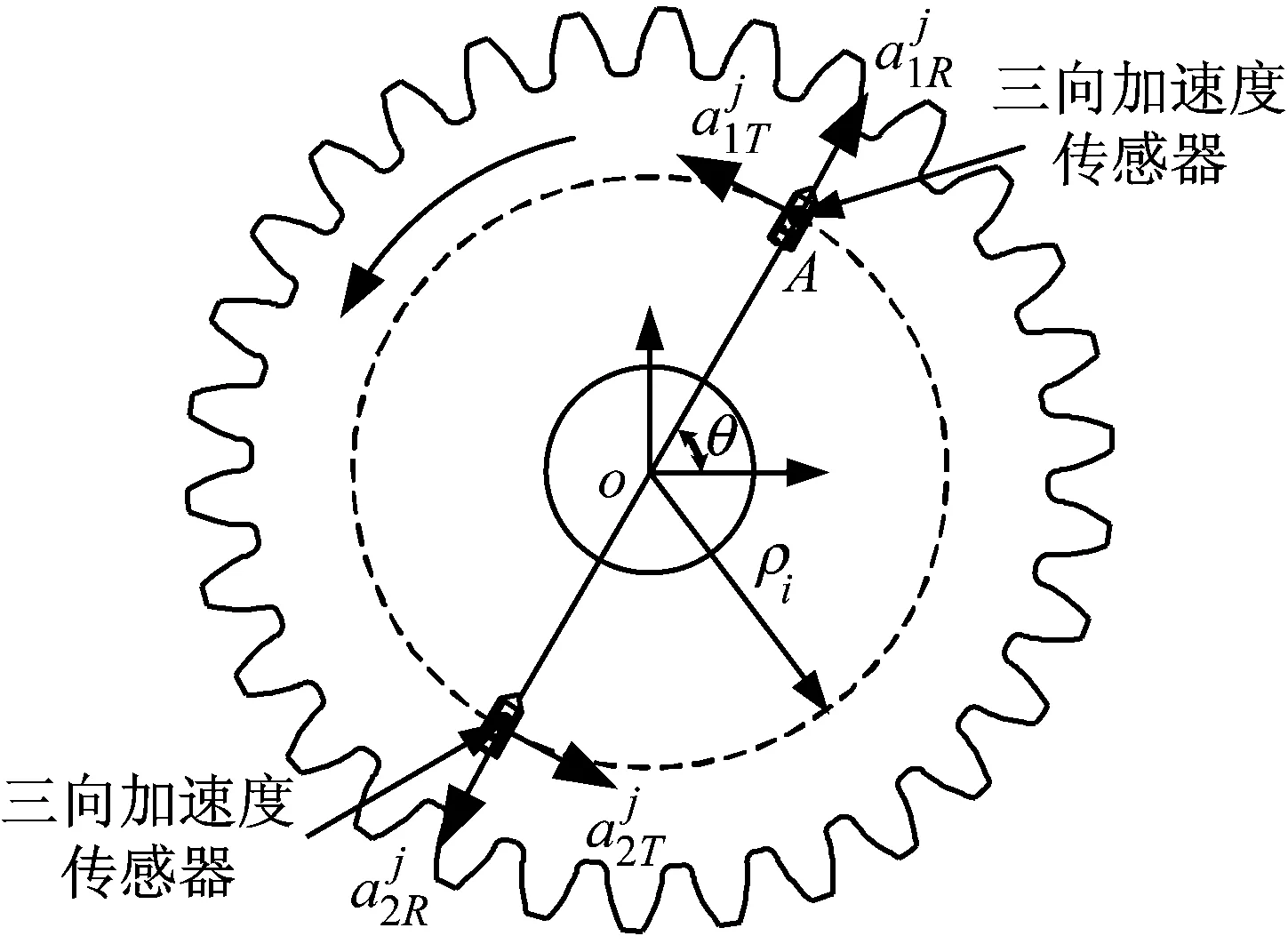
图7 加速度传感器安装示意图
齿轮传动系统的横向振动位移信号通过试验箱的输入、输出轴中间截面的水平和竖直方向各安装的电涡流位移传感器测试。电涡流位移传感器的信号线通过箱盖上预留的导线孔伸出与控制器相联,从控制器出来的信号线直接与数据采集系统相连。轴的平移位移测试原理如图8所示,点O为电涡流位移传感器的安装位置,A′为轴静止时的圆心位置,A为轴变形后圆心位置,轴的半径为R,电涡流测试方向上轴的位移为c′c。设A′的初始偏移测量方向的距离为y0,即A′B′=y0,轴相对于初始位置的位移为(x,y),即B′B=x,AB=y0+y,电涡流测试方向上轴的位移C′C为
C′C=x+C′B′-CB=

(58)
横向振动位移峰峰值dp-p定义为
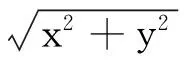
(59)

图8 轴横向振动位移测量原理
在试验箱中间轴的中间部位,按照全桥测量法在轴两端对称位置贴有四个电阻式应变片,用来测试轴扭转切应变。应变片的信号线经集流环、应变桥盒与动态应变仪连接,再由应变仪输出端与数据采集系统连接。由应变仪的读数εd可得轴段扭转切应力τ
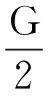
(60)

扭转应力峰峰值τp-p定义为
τp-p=max(τ(t))-min(τ(t))
(61)
为了验证两级齿轮传动系统非线性动力学模型的准确性,分别针对空载条件和受载条件的稳态工况,测试两级定轴齿轮试验装置的振动特性。测试工况为:泵马达输出转矩分别为0 Nm和320 Nm,分别在400 r/min,600 r/min,1 000 r/min,1 200 r/min,1 400 r/min转速下进行测试。由于泵马达后增速箱的作用,受载条件下两级齿轮传动实验装置实际输入扭矩为150 Nm,输入转速依次为850 r/min,1 275 r/min,2 125 r/min,2 550 r/min和2 975 r/min。
3.2 加速度对比分析
采用4阶定步长龙格库塔法求解非线性动力学方程。数值求解时,两级齿轮传动系统的输入转矩和转速与各工况下试验装置实际输入转矩和转速相同。齿轮1和齿轮4的扭转角加速度,计算它的均方根值,将其与仿真计算结果进行对比。各工况下,齿轮1和齿轮4的扭转角加速度均方根值的试验结果和仿真结果及两者之间的误差分别如表3和表4所示。由表可知,随着转速的增加,齿轮1和齿轮4的扭转角加速度均方根值逐渐增加,仿真结果与试验结果的变化趋势基本一致。且各工况下仿真结果与试验结果之间的最大相对误差为23.51%。
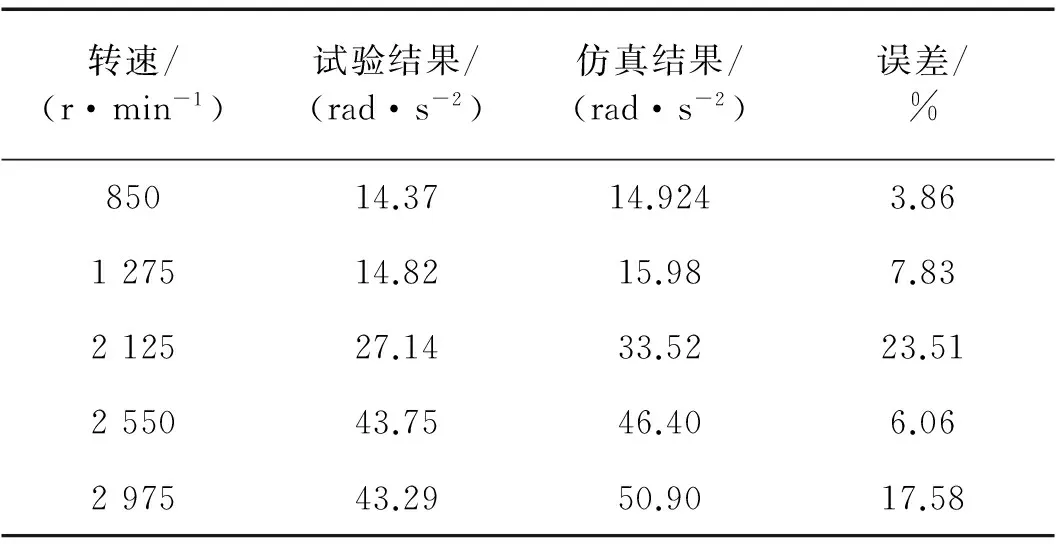
表3 齿轮1角加速度均方根值

表4 齿轮4角加速度均方根值
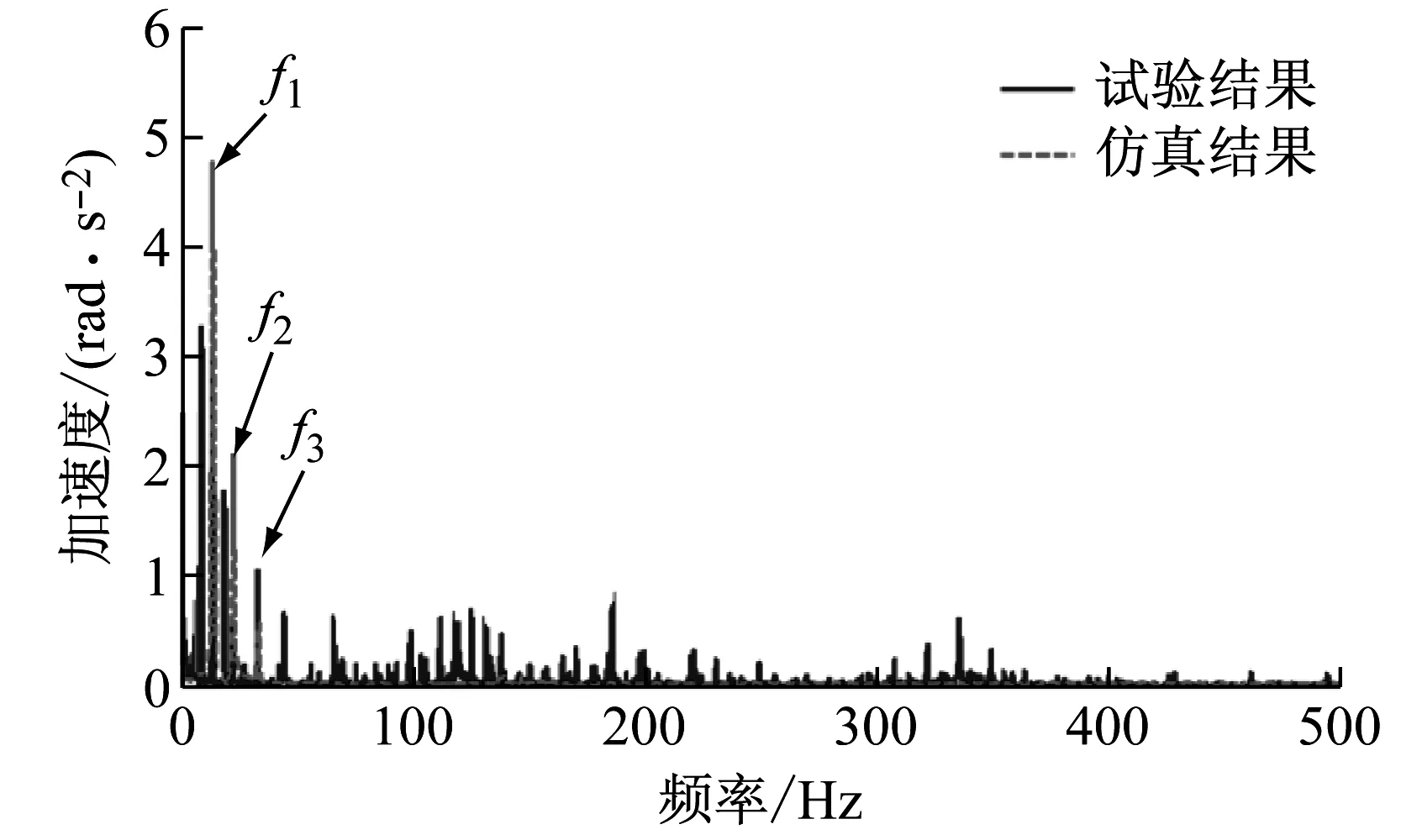
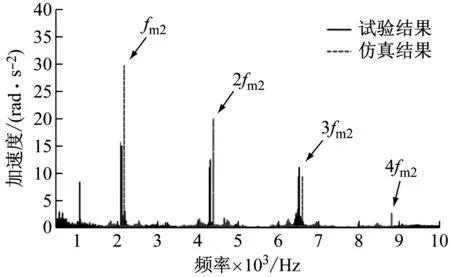
两级定轴齿轮传动系统输入转速为850 r/min时,齿轮1扭转角加速度的试验结果与仿真结果的频谱如图9。由图可知,仿真结果的扭转角加速度在低频区[0,500 Hz]内以三个轴的转频为主,其他频率成份的幅值很小。相比而言,试验结果在低频区不仅包含各轴的转频,还包含一些无法分析出产生原因的频率成份。同时仿真结果与试验结果在各转频对应的幅值上大小略有不同。高频区[500 Hz,10 000 Hz]内,齿轮1的扭转角加速度的仿真结果以啮频及其倍频为主,同时出现了第二级齿轮传动的啮合频率。相比而言,试验结果在高频区内不仅存在啮频及其倍频,还出现了第二级齿轮传动的啮频及其2倍频,同时在啮合频及其倍频附近出现了一些组合频率。其中,仿真结果与试验结果在各啮频及其倍频对应的幅值上大小略有不同。输入转速为850 r/min时,齿轮4的试验结果与仿真结果的扭转角加速度频谱对比如图 10所示。由图可知,齿轮4的扭转角加速度试验结果与仿真结果均以各轴转频、啮频及其倍频为主。同样,试验结果所包含的频率成份更为丰富。仿真结果与试验结果在各转频、啮频及其倍频对应的幅值上大小略有不同。
(a)

(b)

(a)
(b)
3.3 振动位移对比分析
由于位移测点均在传动轴中间位置,结合材料力学法分别计算出齿轮1和齿轮4所在位置的振动位移并计算峰峰值,将其与仿真计算结果进行对比。不同工况下,齿轮1和齿轮4的横向振动位移峰峰值的试验结果和仿真结果及两者之间的误差分别如表5和表6所示,试验结果和仿真结果对比图如图 11所示。可以看出,仿真结果与试验结果的变化趋势基本一致。且各工况下仿真结果与试验结果之间的最大相对误差为21.21%。
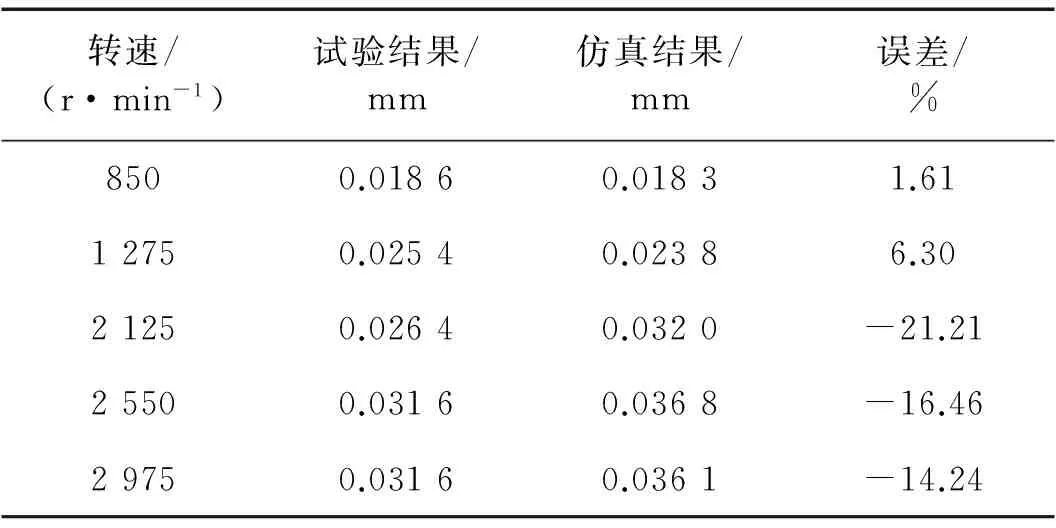
表5 齿轮1横向振动位移峰峰值

表6 齿轮4横向振动位移峰峰值
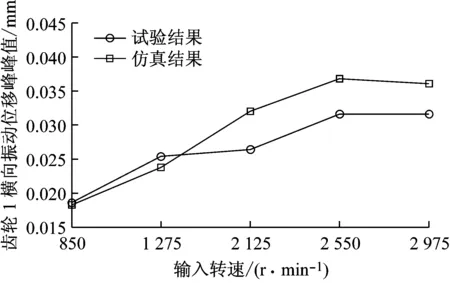
(a) 齿轮1
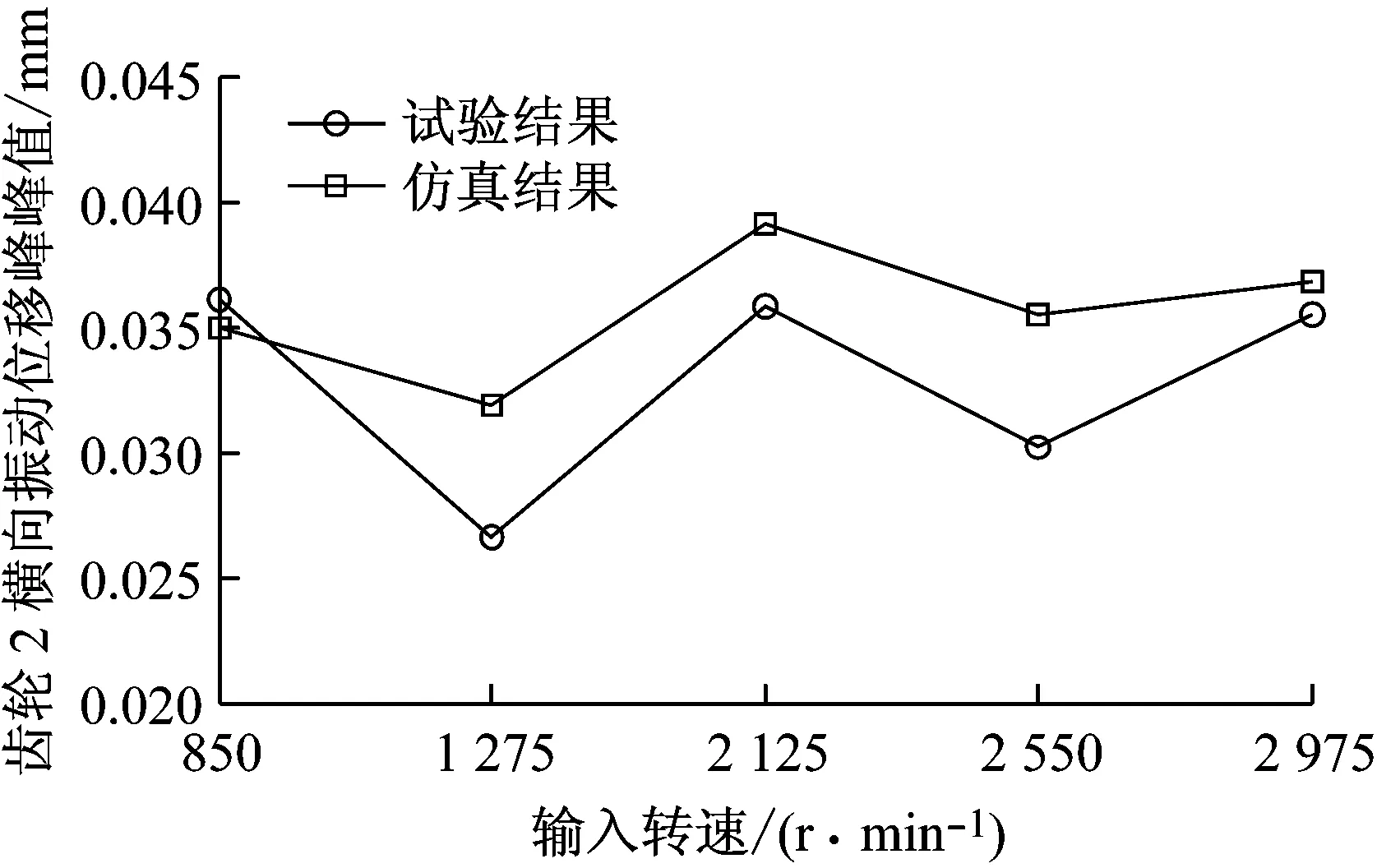
(b) 齿轮4
3.4 扭转切应力对比分析
计算扭转切应力,并计算它的峰峰值作为试验结果。将仿真所得的齿轮2和齿轮3的扭转角度作为边界条件施加到它们之间轴段上得到扭转应力,并计算扭转应力峰峰值。不同工况下,齿轮2与齿轮3之间轴段扭转切应力峰峰值的试验结果和仿真结果及两者之间的误差如表7所示,试验结果和仿真结果的对比图如图12所示。可以看出,随着转速的增加,齿轮2与齿轮3之间轴段的扭转切应力近似呈线性增加,仿真结果与测试结果的变化趋势基本一致。且各工况下仿真结果与试验结果之间的最大相对误差为17.9%。
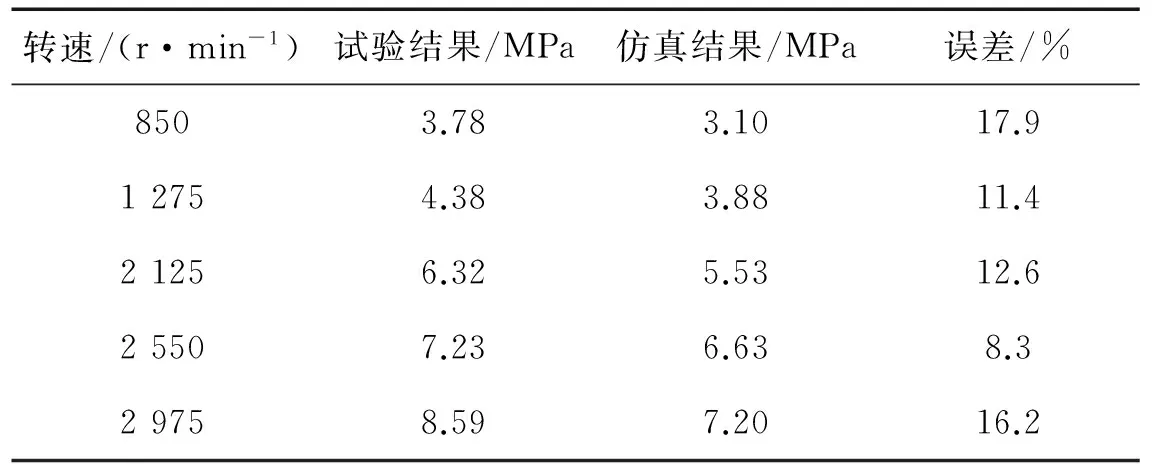
表7 扭转应力峰峰值
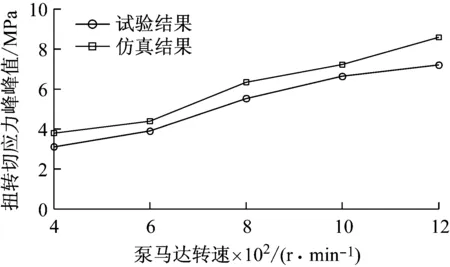
图12 扭转切应力峰峰值对比结果
3.5 误差分析
对于加速度,造成仿真结果与试验结果之间产生误差的主要原因有以下几个方面:
1) 模型中的质量、惯量、刚度、阻尼、偏心和偏载力矩等参数是真实系统的一种等效,这种等效在很大程度上取决于建模经验,尤其是系统的弯曲阻尼、扭转阻尼和啮合阻尼等阻尼参数一般很难确定,与系统真实参数存在一定差距;
2) 由于齿轮实际加工和安装误差,齿面摩擦和磨损,轮齿间的油膜润滑等的作用,导致啮合刚度和齿形误差等与啮合频相关的参数激励不断变化,造成仿真结果在高频振动成份及其对应幅值上与试验结果之间存在误差;
3) 模型中仅对两级定轴齿轮传动系统进行动力学建模,忽略了前、后传动箱和被试件箱体等部件的影响,而试验过程中上述部件的振动必然会对齿轮传动系统的振动产生影响,从而产生一些无法分析出原因的低频成份;
4) 数值仿真中的输入扭矩和转速均取为定值,而试验过程中泵马达输出转矩和转速无法始终保持恒定,同时输出转矩和转速要经过联轴器和前传动箱等部件,上述因素对两级定轴齿轮传动系统的实际输入存在一定影响;
5) 加速度传感器的安装位置和方向与理论安装位置和方向存在一定的偏差,同时实际测试系统中存在白噪声以及多个轴承旋转形成的干扰噪声,上述因素均会对试验结果产生一定的影响。
对于振动位移,造成仿真结果与试验结果之间产生误差的主要原因除了与加速度误差分析中的前四项相同外,还包括以下几个方面:电涡流传感器并非严格对准轴心位置;在将传动轴中间处位移向各齿轮处位移等效时,并未考虑轴承变形和箱体变形等因素的影响;在测量过程中安装在箱体上的电涡流传感器会随着箱体的振动而振动。
对于扭转切应力,造成仿真结果与试验结果之间产生误差的主要原因除了与加速度误差分析中的前四项相同外,还包括以下几个方面:实际系统的传动轴上存在油孔和传感器线导出空等,从而导致局部应力集中,而仿真中将轴简化为规则的圆轴,造成各工况下试验结果始终大于仿真结果;由于数据采集前端的采样频率高于动态应变仪的采样频率,造成大量系统噪声混入有效数据;应变片的粘贴工艺、连接导线的阻抗和应变仪自身测量误差都会对测试信号形成干扰。
4 结 论
(1) 本文考虑了齿轮副的弯曲位移引起的啮合角的时变性,基于渐开线齿轮传动的特点分析了瞬时啮合点压力角与齿轮转速的关系,并采用压力角确定单双齿啮合边界条件,结合为weber材料力学法建立了是齿轮啮合时变刚度反馈模型,并编写了计算程序,该程序可实现与动力学方程的实时反馈,精确的描述了齿轮传动过程中接触状态。
(2) 研究了试验装置的加速度信号、位移信号和应变信号的测试方法、测试原理和数据处理方法。对比分析了多个稳态工况下齿轮传动系统的角加速度、振动位移和扭转切应力数值仿真结果与试验结果,并分析了可能导致仿真结果与试验结果之间产生误差的原因。结果表明,各工况下角加速度、振动位移和扭转切应力仿真结果与试验结果最大误差分别为23.51%、21.21%和17.9%。仿真结果与试验结果的变化趋势基本吻合,且误差在可接受范围内。验证了本文提出的渐开线直齿轮传动横-扭-摆耦合非线性动力学模型和非线性动态啮合模型的正确性。
[1] 李润方, 王建军. 齿轮系统动力学[M]. 北京: 科学出版社, 1996.
[2] WANG Jianjun, LI Runfang, PENG Xianghe. Survey of nonlinear vibration of gear transmission systems[J]. ASME, 2003: 309-329.
[3] KAHRAMAN A, SINGH R. Interactions between time varying mesh stiffness and backlash non-linearity in a geared system[J]. Journal of Sound and Vibration, 1991,146:135-156.
[4] WALHA L, FAKHFAKH T, HADDAR M. Nonlinear dynamics of a two-stage gear system with mesh sti_ness uctuation, bearing exibility and backlash[J]. Mechanism and Machine Theory, 2009, 44: 1058-1069.
[5] 崔亚辉, 刘占生, 叶建槐. 齿轮-转子耦合系统的动态响应及齿侧间隙对振幅跳跃特性的影响[J].机械工程学报,2009,7,45(7):7-15.
CUI Yahui, LIU Zhansheng, YE Jianhuai. Dynamic response of geared rotor system and the effect of clearance on jump characteristics of amplitude[J]. Chinese Journal of Mechanical Engineering, 2009, 45(7):7-15.
[6] SKRICKIJ V, BOGDEVICIUS M. Vehicle gearbox dynamics: centre distance inuence on mesh stiffness and spur gear dynamics[J]. Transport, 2010,25:278-286.
[7] KIM W, YOO H H, CHUNG J. Dynamic analysis for a pair of spur gears with transla-tional motion due to bearing deformation[J]. Journal of Sound and Vibration, 2010,329:4409-4421.
[8] CHEN Siyu, TANG Jinyuan, LUO Caiwang, et al. Nonlinear dynamic characteristics of geared rotor bearing systems with dynamic backlash and friction[J]. Mechanism and Machine Theory, 2011,46:466-478.
[9] CHEN Z G, SHAO M, LIM T C. Nonlinear dynamic simulation of gear response under the idling condition[J]. International Journal of Automotive Technology, 2012, 13: 541-552.
[10] ZHANG Yimin, WANG Qibin, MA Hui, et al. Dynamic analysis of three-dimensional helical geared rotor system with geometric eccentricity[J]. Journal of Mechanical Science and Technology, 2013,27(11):3231-3242.
[11] WEBER C. The deformation of loaded gears and the e_ect on their load-carrying capacity[M]. Sponsored Research (Germany) Department of Scientific and Industrial Research Report, Germany,1949.
[12] CORNELL R W. Compliance and stress sensitivity of spur gear teeth[J]. Journal of Mechanical Design, 1981, 103:447-458.
[13] SAINSOT P, VELEX P, DUVERGER O. Contribution of gear body to tooth deflections-a new bi-dimensional analytical formula[J]. Journal of Mechanical Design, 2004,126:748-752.
[14] CHAARI F, FAKHFAKH T. Mohamed haddar dynamics of mechanical systems research unit, mechanical engineering department, national school, analytical modelling of spur gear tooth crack and influence on gearmesh stiffness[J]. European Journal of Mechanics A/Solids, 2009,28:461-468.
[15] CHEN Zaigang, SHAO Yimin. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth[J]. Engineering Failure Analysis, 2011, 18:2149-2164.
Nonlinear dynamic modeling and test validation for a two-stage involute gear system
LIU Hui1, ZHANG Chen1, WANG Cheng2
(1. School of Mechanical and Vehicular Engineering, Beijing Institute of Technology, Beijing 100081, China;2. Chinese North Vehicle Research Institute, Beijing 100072, China)
Here, a two-stage involute gear system was taken as a study object, the effects of variation of distances between centers due to geometric eccentricity, installation errors of distances between centers and bending displacement of gear center bearings on pressure angle and backlash were analyzed, a nonlinear dynamic meshing stiffness model was introduced, nonlinear dynamic meshing forces of each gear pair were obtained. Adopting Lagrange method, the nonlinear lateral-shimmy-torsional coupled dynamic model of the two-stage involute gear system was established considering the effects of eccentricity, backlash, time-varying pressure angle and the nonlinear dynamic meshing stiffness model. The nonlinear dynamic equations were solved with the 4th order fixed step Runge-Kutta algorithm. The theoretical calculation and tests were performed for a test device of a two-stage gear system. The test results showed that the maximum error between simulated values of angular acceleration under various conditions and tested ones obtained with angular acceleration sensors installed at symmetric positions around gear circumference is 23.51%; the maximum error between simulated values of vibration displacements and tested ones obtained with displacement sensors installed at positions of the gear box is 21.21%; the maximum error between simulated values of torsional shear stresses and tested ones obtained with strain gauges pasted on the gear shaft is 17.9%. The study results indicated that the varying trend of simulated results agrees well with that of test ones, and errors are within an acceptable range, the reasons causing errors between simulated results and tested ones are analyzed; the correctness of the proposed dynamic model and the meshing stiffness model of the gear system is verified.
two-stage involute gear system; nonlinear; backlash; test validation; pressure angle
国家自然科学基金(51375047);教育部新世纪人才支持计划资助(NCET-12-0043)
2016-02-29 修改稿收到日期:2016-06-03
刘辉 女,博士,教授,1975年生
TH113.1
A
10.13465/j.cnki.jvs.2017.15.019
