单层双向偏心结构振型影响参数推导分析
2017-08-30姜忻良
姜忻良, 韩 阳
(天津大学 建筑工程学院 滨海土木工程结构与安全教育部重点实验室, 天津 300072)
单层双向偏心结构振型影响参数推导分析
姜忻良, 韩 阳
(天津大学 建筑工程学院 滨海土木工程结构与安全教育部重点实验室, 天津 300072)
为了深入分析单层双向偏心结构平扭耦联参数的影响规律,建立单层双向偏心结构(3自由度)的动力方程,并采用数学领域中三次方程求解的盛金公式,推导出单层双向偏心结构的动力特性显式解析解。根据所得显式解的形式及其对应的判定条件,在合理范围内提取出不同于单向偏心体系的影响参数,分别为:相对偏心距、偏心角、主扭平频率比以及次扭平频率比。根据盛金公式推导所得的显式解析解,总结出结构的主要动力特性指标(频率和振型),进而分析了每个参数对双向偏心结构的平扭耦联特性的影响。结果表明,双向偏心结构平扭耦联参数与单向偏心结构有相似之处,但更为复杂,会涉及到主扭平频率比与次扭平频率比,且两者影响程度也有明显区别。
双向偏心结构;解析解;影响参数;偏心距;偏心角;扭平频率比
随着结构的多样化和复杂化发展,偏心结构的动力特性分析已经成为结构工程领域研究者的一个重要课题。不少专家学者在这方面取得了丰硕的成果[1]。早在20世纪80年代Hejal等[2]研究了偏心率e/r和平扭刚度比Ω对多层框架结构扭转反应的影响,指出扭转反应随偏心率的增大而增大,当平扭刚度比接近1时平扭耦联效应最为明显。
近些年来,不少学者在此基础上对偏心结构的动力特性研究取得了一定的成就[3-9]。但是现在所取得的成果和所使用的理论依据仍然是以单向单层偏心体系(2自由度)为研究对象所得到的。有些研究虽然以双向偏心结构为研究对象,但是所使用的理论却是由单向单层偏心公式所求得的。
我们不难想象,一个结构在实际工程中很少是单向偏心的。随着现代人类的文明进步与审美提升,越来越多的复杂结构拔地而起。当今社会许多结构都是双向偏心结构,因此应该着眼于此,从理论上系统的推导双向偏心体系的有关规律并进行总结。
当前动力学所研究的理论公式基本都是基于1个或2个自由度的体系,因为选取这样的研究对象能够很好的使用现有的数学理论,将结构的频率和振型的解析解推导出来。得到含有各个参数的解析解后,我们可以容易地分析出结构动力响应中的各影响参数以及它们各自的影响程度。
研究三个自由度的体系时,当今动力学类科学刊物以及相关论文大量采用例算法,即自定义一结构,进行模拟计算,从而得到所需结论。但是运用这种方法很难从理论上进行参数化分析,只能通过大量的算例来进行说明,尚无清晰的理论依据,或者仅能从两个自由度算例的结论中寻求解释。同时,由于算例的局限性,可能某一系列算例并不能反应所有参数可能的变化情况。
同时还应注意,平扭耦联特性主要受到结构自身动力特性影响,而这种影响应该分为两个部分。一部分是结构各振型之间的耦联;另一部分是结构某个基本振型内各位移分量之间的耦联。以往的分析经常忽视这一方面的归纳,即使得到正确的结论也可能阐述的不够明确。如果能求出结构动力特性的解析解,势必会使这一部分的分析更加清晰明了,因此求解单层双向偏心结构的动力特性解析解十分重要。
为了更加系统地分析双向偏心结构(三自由度体系)的动力参数影响,求解此体系的解析解表达式便是重点。本文将动力学基本方程与数学领域中的盛金公式结合起来,推导结构频率与振型的解析解公式,从而更加系统明确的分析此体系的动力影响参数,并为以后分析多层双向偏心体系做准备。
1 单层双向偏心体系运动方程推导
图1为一单层双向偏心简化模型的平面示意图,静力偏心距为δ,偏心角为α(此处定义为质心与刚心连线与笛卡尔坐标系下的X轴夹角)。抗侧力构件的刚度在两个方向分别设为为kx和ky。

图1 单层双向偏心简化模型的平面示意图
在不考虑阻尼的条件下,结构的动力方程为:
(1)
式中:j=m*r2,r为转动半径;当自由振动时P=0,两边除以m,最后一行除以r,可导出下式:
(2)
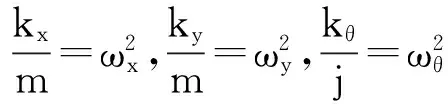
(3)
设每一阶振型的平动与转动位移可以由以下形式表示:
ux=Xsin(ωt+φ)
uy=Ysin(ωt+φ)
uθ=Θsin(ωt+φ)
(4)
代入上式中整理得
(5)
提取左边矩阵第一行和右边矩阵进行运算得:
(6)
解得:
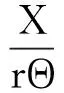
(7)
提取左边矩阵第二行和右边矩阵进行运算得:
(8)
解得:
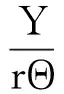
(9)
联立可得:
(10)
此处X代表结构X向的平动位移,Y代表结构Y向的平动位移,rΘ代表结构由于扭转产生的扭转位移。这样表述,可以使三种位移的量纲统一为长度单位,尤其是对分析扭转效应而言,能够更明确地在同量纲下分析各种位移的反应规律。
根据上式可以看出,结构的自身动力特性与结构的相对静力偏心距B,结构偏心角α,结构X向、Y向平动频率ωx、ωy以及结构的频率ω有关。其中结构的频率是未知量,其余均为已知量,如果能够通过显式求解出结构的频率可以更好的进行接下来的分析工作。
求解结构的频率ω如下:
(11)
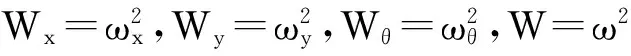
整理得到:
(12)
展开得到:
W3+(-Wx-Wy-Wθ)W2+(WxWθ+WxWy+WyWθ-
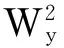
(13)
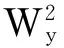
则上述方程可化为ax3+bx2+cx+d=0的方程形式,根据盛金定理,该方程有解析解,解法如下:
若方程为:ax3+bx2+cx+d=0,
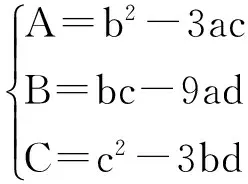
则重根判别式为:Δ=B2-4AC
当A=B=0时,方程有一个三重实根;
当Δ>0时,方程有一个实根和一对共轭虚根;
当Δ=0时,方程有三个实根,其中有一个二重根;
当Δ<0时,方程有三个不相等的实根。
根据本研究的物理意义,模型的三阶频率必为三个不相等的实根或有二重根的三个实根。因此Δ必定小于0或等于0。
当Δ=B2-4AC<0时,根据盛金公式,方程的解为:
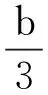

(14)
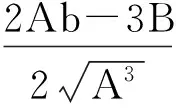
由于等号右边的参数均由已知量B,α,ωx,ωy和ωθ组成,将各参数代入式(14),便可得出精确解。
当Δ=B2-4AC=0时,根据盛金公式,方程的解为:
(15)
由于等号右边的参数均由已知量B,α,ωx,ωy和ωθ组成,将各参数代入式(15),便可得出精确解。
值得注意的是,由于只有双向刚度偏心相等的少数特定结构有两阶相等的频率,大部分结构的三阶频率均不相等,有二重根的情况可以看成是特例,不是本文的重点讨论内容,以下的内容将以三个不相等实根的例子为研究对象。
根据上述公式可以看出,最终求解出的x1、x2、x3中均包含系数a,b,c,d。而x1、x2、x3的值分别代表结构各阶频率ω1,ω2,ω3的平方;系数a,b,c,d包含结构的相对静力偏心距B,结构偏心角α,结构X向、Y向平动频率ωx,ωy和结构扭转频率ωθ,也就是说影响结构每一阶自身频率的影响参数为:B,α,ωx,ωy和ωθ。
上述内容求出了显式解析解,可以采取改变单一参数而其它参数不变的方法,进一步分析某一参数的具体影响。这样分析与以往应用算例方法分析相比更加合理,摆脱了模型的束缚,能够保证排除其他参数改变造成的影响,从而对某一影响参数的改变进行数据分析。
2 单层双向偏心体系公式推导解的验证
为了验证上述公式的正确性,使用频率方程试算法对单层双向偏心算例进行求解,得到模型的三阶频率值,并与本文所推导的计算公式求出的解进行比较,分析本文所推导的原理是否准确有效。
以一单层简单框架为例,结构平面图如图2所示。选取结构平面尺寸为6 m×6 m。层高3.6 m,楼板厚100 mm。梁截面为400 mm×300 mm,1至3号柱截面尺寸为300 mm×300 mm,4号柱尺寸400 mm×350 mm,结构存在刚度偏心。楼板混凝土为C30、梁柱混凝土为C40。混凝土采用Rusch模型。活载3 kN/m2。根据《建筑抗震设计规范》(GB 50011—2010)[10],计算地震作用时,活载的组合值系数取0.5。

图2 模型平面图(mm)
按照本文提出的公式方法与频率方程方法得到频率对比,如表1所示。
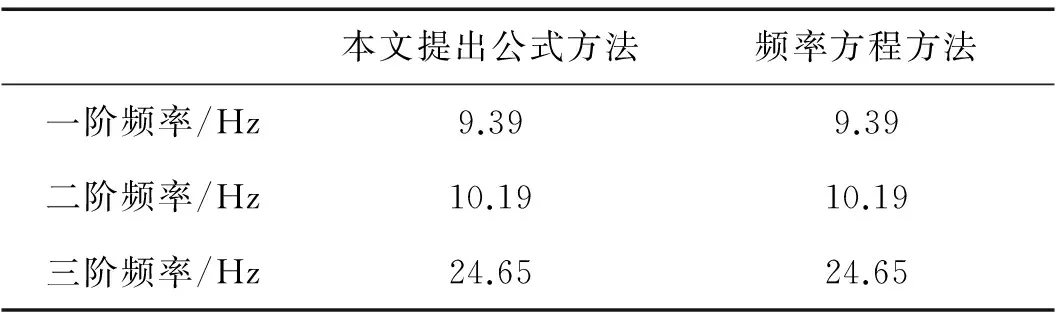
表1 计算频率值对比表
为了更好的分析各个参数对结构的影响,下文将采取变化单一参数的方法,对结构的频率和振型变化进行分析。
3 影响参数分析
本文运用盛金公式,根据单层双向偏心结构的动力方程求解出显式解析解,进而提取出各动力影响参数,因此可以不受模型的约束,进行各影响参数的独立调整,以便得到能反映各参数独自的影响规律。本文的方法可以在实际工程存在的范围内,直接分析各参数的影响规律,适用于任何单层双向偏心体系。
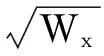
平扭耦联反应主要分为不同振型之间的耦联以及振型自身内各分量的耦联,以下分析将从这两部分入手。为了方便观察,根据振型的特点,将扭转分量幅值定为1,其他幅值进行归一化处理。这里值得注意的是,本文求出的显式解中涉及到偏心角α的项均为sin2α和cos2α,也就是说仅研究0°≤α≤90°范围内(即第一象限)即可,其余范围的偏心角均可按照三角函数平方的对应关系直接参照第一象限的结果得出。例如:α取30°的结果等于α取150°、210°和330°的结果。
3.1 相对偏心距B的影响
分析中,以相对偏心距B为变量,其他参数为常量。因此可以随机设定其他影响参数Wx=100,Wy=110,Wθ=120,α=36°(以第一象限为例,其他象限同理)。当B取合理范围0.1~1时可得曲线,如图3所示。
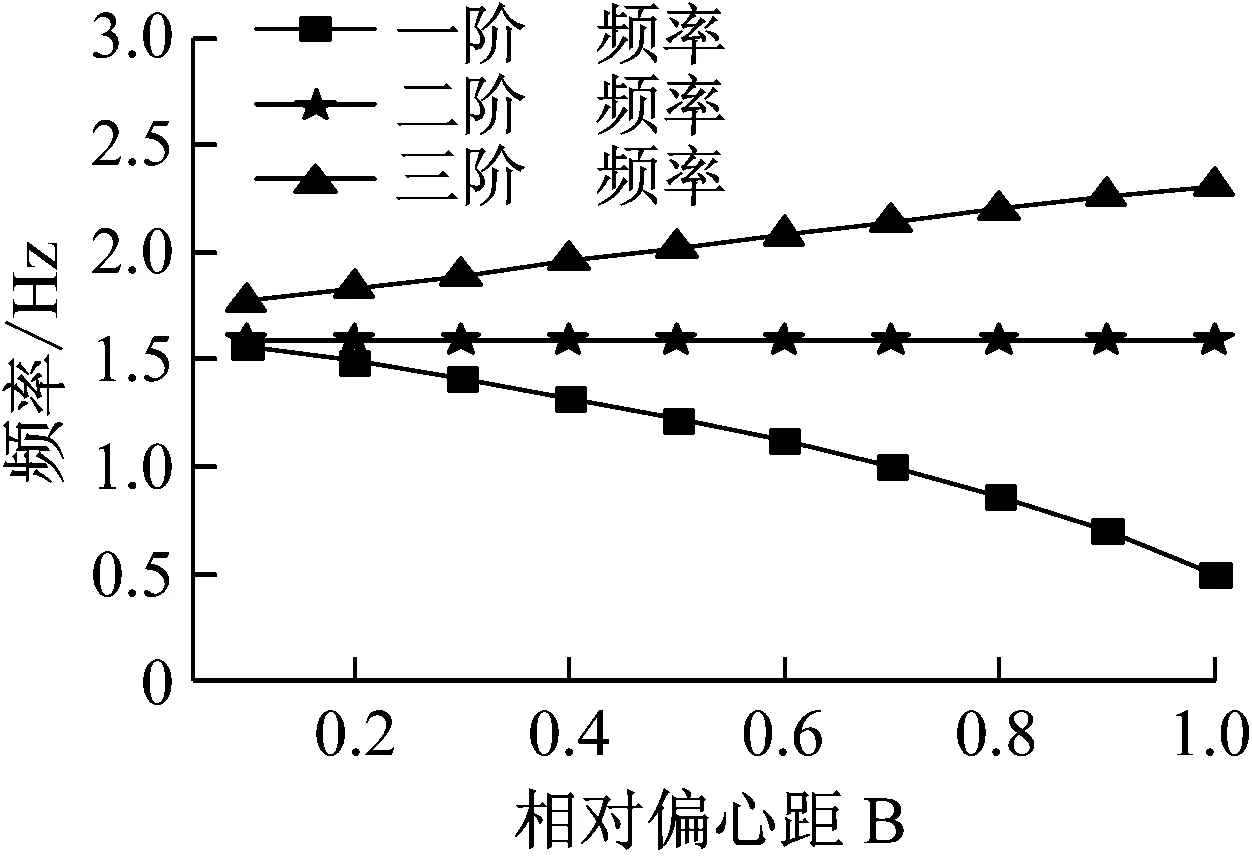
图3 各阶频率随相对偏心距的变化
由图3可以看出,随着结构相对偏心距的增加,结构的一阶频率逐渐降低,二阶频率基本保持不变,三阶频率则呈现上升的趋势。这说明随着偏心距的增加,结构各振型之间的耦联效应是降低的。
由图4~图6可看出,相对偏心距的改变影响结构的振型形式。随着相对偏心距的增大,图4中结构第一振型逐渐由平动为主发展为扭转为主,而图5中二阶振型的双向平动分量逐渐增加,扭转分量逐渐降低,图6中三阶振型保持扭转为主,而双向平动分量略有提高。在通常条件下,结构的动力反应以一阶振型为主时,结构的扭转效应随着偏心距的增大而不断提升。

图4 一阶振型随相对偏心距的变化

图5 二阶振型随相对偏心距的变化

图6 三阶振型随相对偏心距的变化
偏心距增加的过程中,各振型间的耦联效应降低,但其基本振型(一阶振型)的扭转分量幅值所占比重逐渐增加。从图4中我们可以看出,随着偏心距在0.1~1的范围逐渐增加,三个振型耦联效应逐渐减弱,动力反应中第一振型的影响越来越重要,且第一振型中的扭转幅值所占比重也越来越大。因此,结构的扭转反应随着相对偏心距B的增加而增加。
3.2 偏心角的影响
分析中,以偏心角α为变量,其他参数为常量。因此可以随机设定Wx=100,Wy=110,Wθ=120,B=0.2。当α按第一象限(二、三、四象限同理)合理范围0°~90°取值时时可以得到如下曲线:
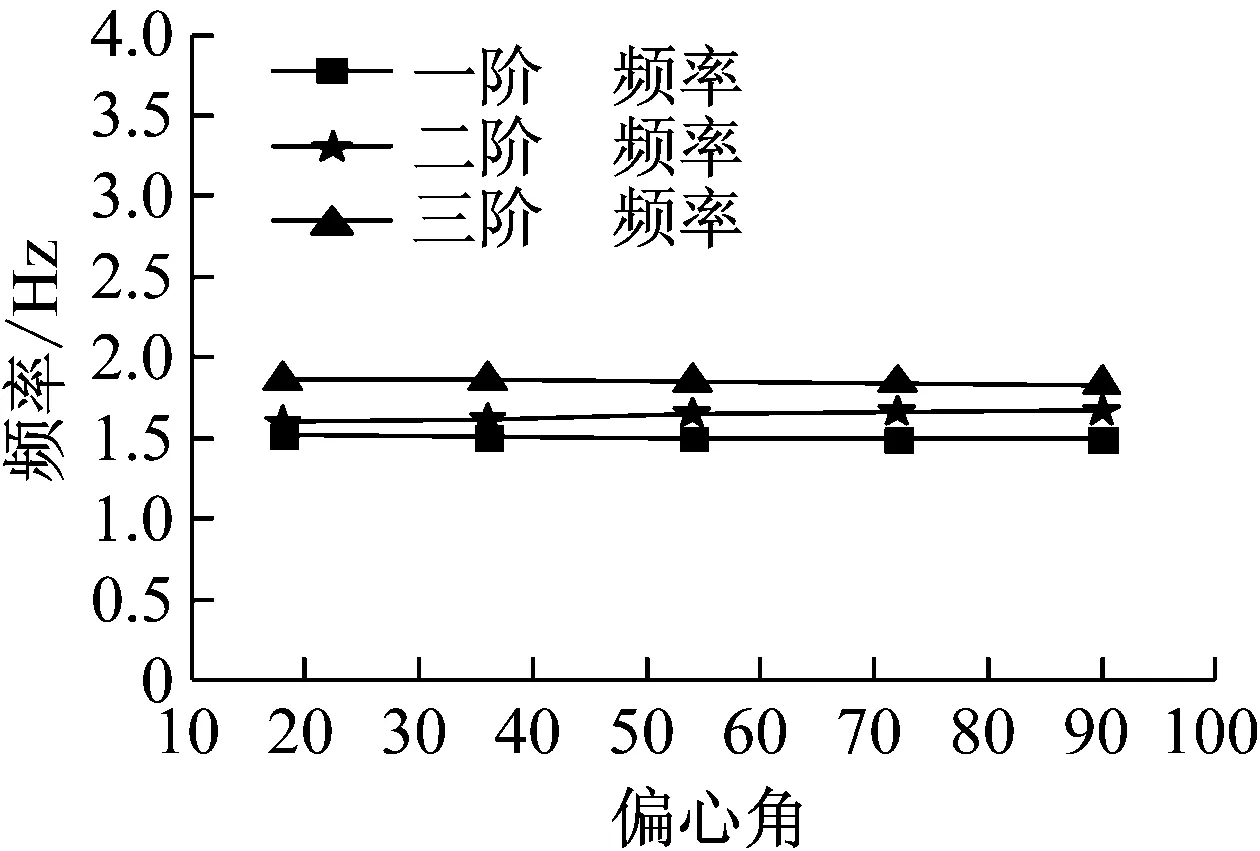
图7 各阶频率随偏心角的变化
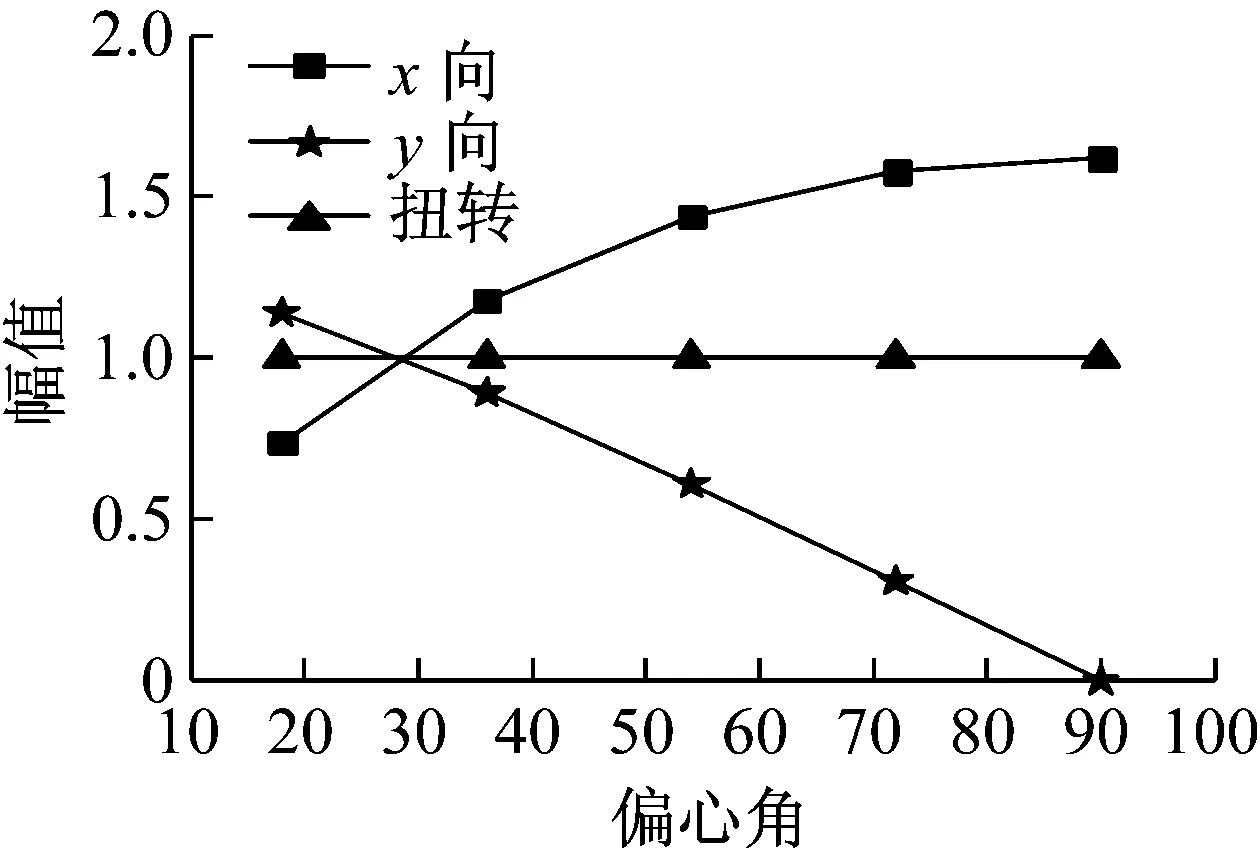
图8 一阶振型随偏心角的变化

图9 二阶振型随偏心角的变化
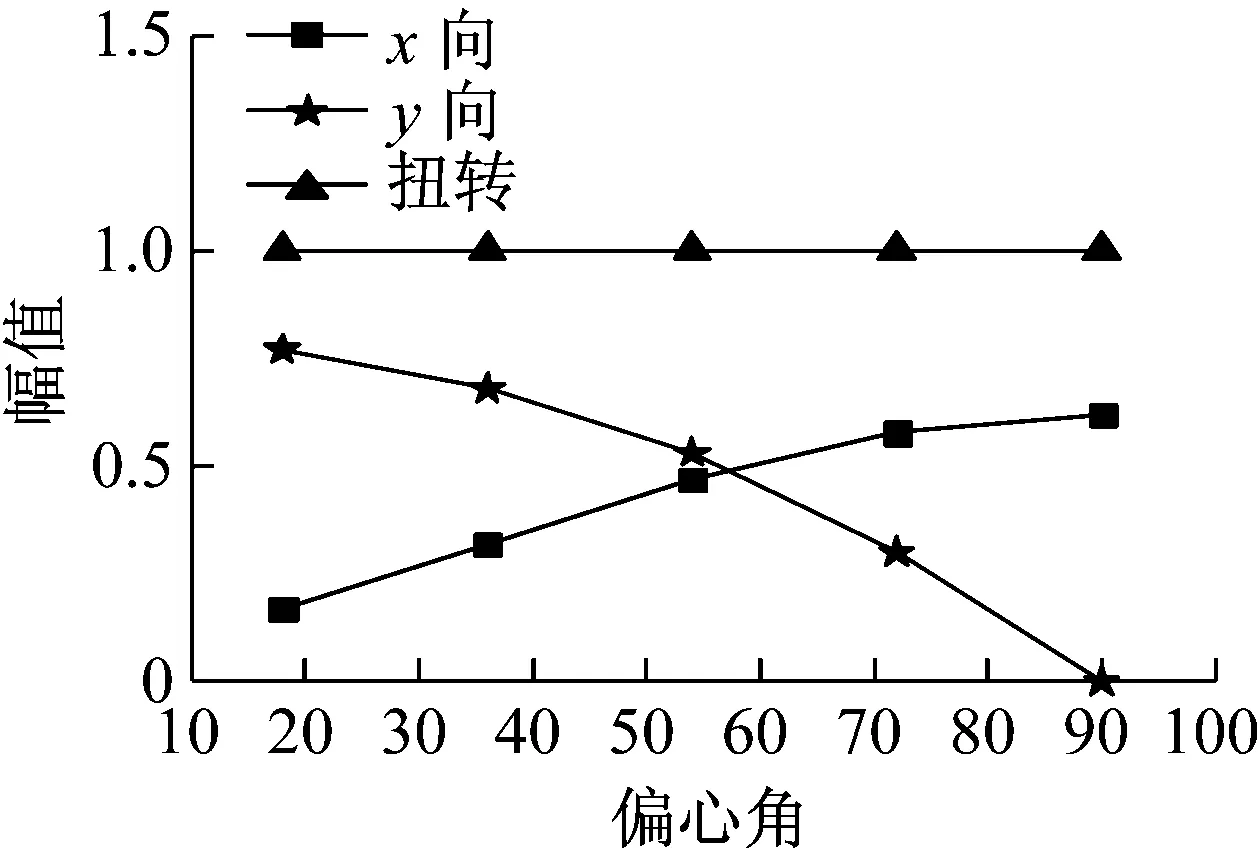
图10 三阶振型随偏心角的变化
由图7可知,随着偏心角的增大,虽然结构各阶频率逐渐变化,但是变化程度较小。在偏心角较小时,二阶频率与一阶频率接近;随着偏心角的增大,二阶频率逐渐远离第一阶频率发展为与三阶频率接近,一频率逐渐占据主要影响地位。三个自振频率变化程度与相对偏心距分析时要小,这说明偏心角对不同振型之间的耦联关系有一定影响,但程度小于相对偏心距。
从图8~图10可以看出,偏心角的变化对X向平动分量与Y向平动分量的影响远大于对扭转分量的影响。从图7可知,第一振型的影响随着偏心角增大而逐渐提升。从图8中看出,影响最大的一阶振型随着偏心角的增加,X向平动逐渐减小,Y向平动逐渐增加,说明偏心角影响着结构动力反应中的不利方向。当偏心角取30°左右时,X向平动、Y向平动和扭转幅值最为接近,此情况下结构振型内的平扭耦联效应最强。要注意的是,这个范围有可能会伴随其他参数的变化而发生变化,但是偏心角与扭转反应关系的变化趋势是不变的,即随着偏心角由0°增加至90°(以第一象限为例,其他同理),结构各振型的自身平扭耦联效应呈现先增强后减弱的特征。
3.3 频率比的影响
单层双向偏心结构的平扭耦联动力特性受三个固有频率ωx、ωy和ωθ的影响。根据本文运用盛金公式求得显式解的推导部分可知,频率之间的关系会影响结构的动力特性。现定义主扭平频率比和次扭平频率比如下。
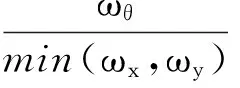
3.3.1 主扭平频率比分析
根据上述定义,我们可以更简便的对结构动力特性进行参数分析。选取偏心角α=45°,相对偏心距B=0.2,设X向抗侧刚度小于Y向。当主扭平频率比在0.9~1.4变化,次扭平频率比保持0.8不变时,结构的三阶频率变化,如图11所示。
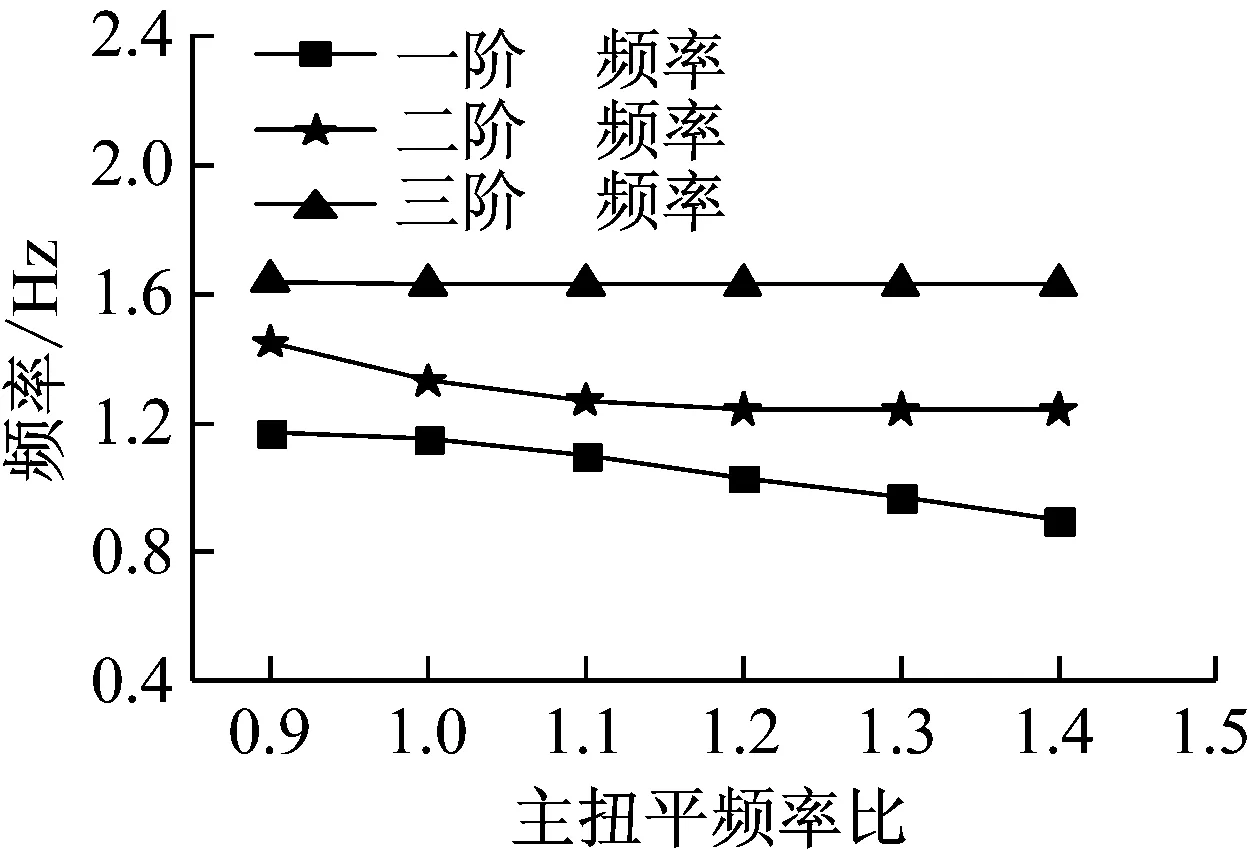
图11 各阶频率随Ω1的变化(Ω2=0.8)
由图11可知,随着主扭平频率比的增大,结构的一阶频率和二阶频率呈逐渐下降的趋势,三阶频率基本不变。总体而言,一、二阶频率较为接近,但一阶频率下降程度比二阶频率要大。也就是说,随着主扭平频率比的增大,结构按一阶振型进行动力反应的程度要大于二、三阶振型。随着主扭平频率比增大,结构的动力反应逐渐以一阶振型为主。
根据图12~图14可知,结构一阶振型由扭转为主逐渐发展为X向平动为主、二阶振型由X向平动为主发展为扭转为主、三阶振型保持Y向平动为主。由图12可知,结构主扭平频率比在1附近取值时,一阶振型扭转幅值和平动幅值很接近,这使得结构会发生较强的平扭耦联效应,扭转效应明显;当Ω1>1时,该方向平动分量显著增加,远大于扭转分量,振型内的扭转效应减弱。
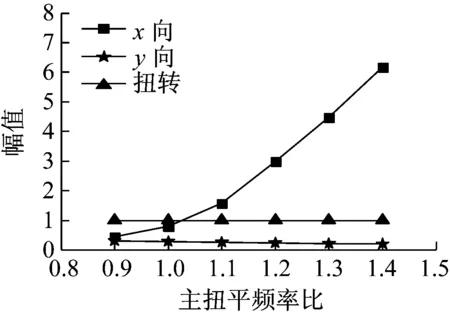
图12 一阶振型随Ω1的变化(Ω2=0.8)
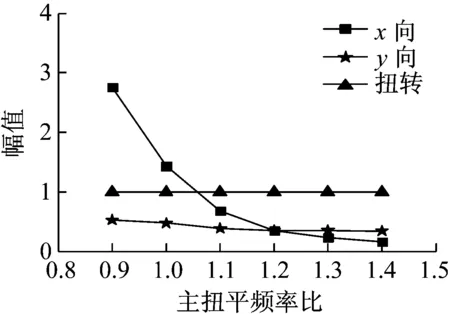
图13 二阶振型随Ω1的变化(Ω2=0.8)
3.3.2 次扭平频率比分析
接下来我们分析次扭平频率比对结构动力特性的影响。偏心角选取α=45°,相对偏心距B=0.2,设X向抗侧刚度小于Y向。当主扭平频率比为1.2,次扭平频率比在0.6~1.1范围内变化时,结构三阶频率,如图15~18所示。

图15 各阶频率随Ω2的变化(Ω1=1.2)
根据图15可以看出,次扭平频率比从0.6增大至0.9的过程中,结构一、二阶频率基本没有变化,一阶频率明显大于二、三阶频率,结构反应以一阶振型为主;随着次扭平频率比从0.9增大至1的过程中,结构各阶频率有所逼近;大于1之后,一二阶频率明显出现接近的趋势,三阶频率有所远离,说明次扭平频率比大于1之后,一二阶振型的耦联效应将有所增加。由图16~图18可以看出,结构一阶振型以X向平动为主,并未随Ω2的增大而改变;二阶振型随Ω2的增加由扭转为主转为Y向平动为主;三阶频率由Y向平动为主转为扭转为主。在Ω2取0.6~1范围时,结构的反应以一阶振型为主时,平动的幅值反应明显大于扭转,次扭平频率比的变化对结构的平扭耦联效应影响较小;随着Ω2的取值大于1之后,二阶频率逐渐接近一阶频率,二阶振型的影响逐渐显现。但由图17可知,当Ω2的取值大于1时,平动幅值大于扭转幅值,二阶振型转为平动为主。因此,次扭平频率比对结构扭转的影响要远小于主扭平频率比。
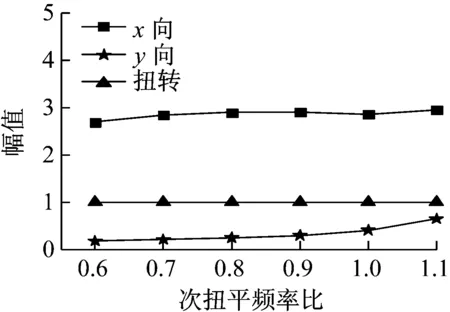
图16 一阶振型随Ω2的变化(Ω1=1.2)
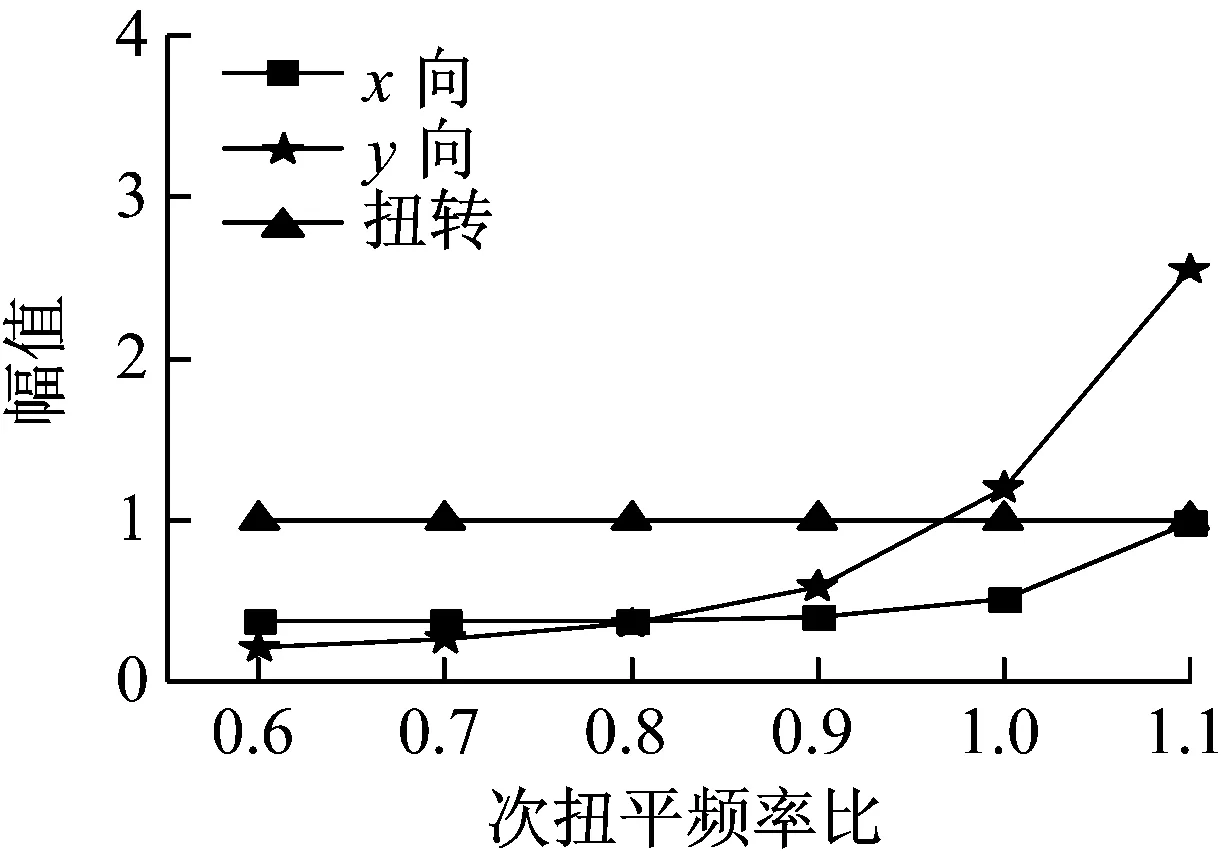
图17 二阶振型随Ω2的变化(Ω1=1.2)
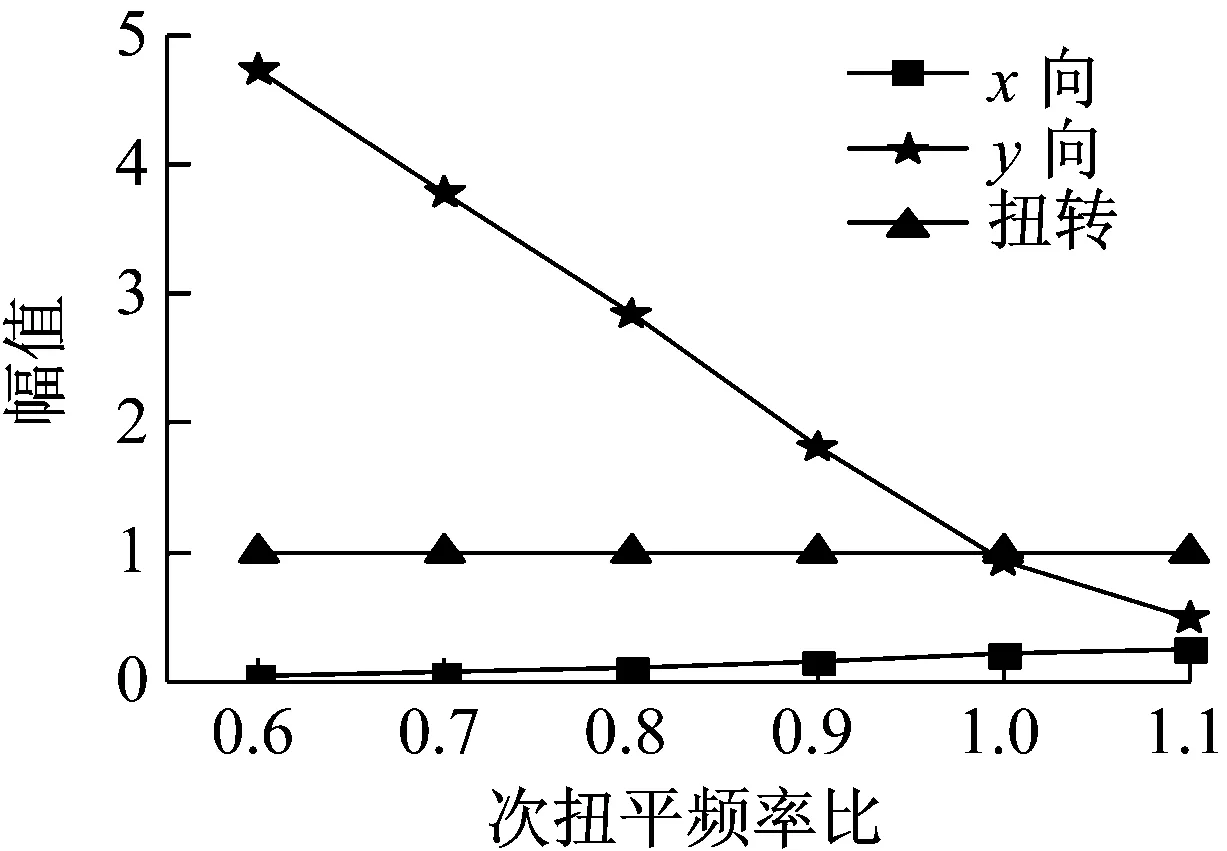
图18 三阶振型随Ω2的变化(Ω1=1.2)
4 结 论
本文根据盛金公式对单层双向偏心结构的动力方程进行求解,得到了显式解析解,并据此提取了单层双向偏心结构平扭耦联动力特性的影响参数,分别为:相对偏心距B、偏心角α以及三个非耦联频率ωx、ωy和ωθ共五种参数。根据解析解的形式,在其它参数不变的条件下改变某一参数的取值,研究其对结构动力特性的影响如下:
(1) 在偏心距增加的过程中,各振型之间的耦联效应呈降低的趋势,但其基本振型中扭转分量幅值占的比重却逐渐增加。随着偏心距在0.1~1范围增加时,三个振型耦联效应越来越低,即动力反应中第一振型越来越占主要地位,且第一振型中的扭转幅值所占比重越来越大。因此,结构的扭转效应随着相对偏心距的增加而增加。
(2) 随着偏心角的增大,结构各阶频率值变化程度较小,这说明偏心角对不同振型之间的耦联程度有一定影响,但是影响程度不如相对偏心距大。随着偏心角的增加,一阶振型的X向平动逐渐减小,Y向平动逐渐增加,说明偏心角也影响着结构不利方向的动力反应。随着偏心角由0°增加至90°,结构各振型的自身平扭耦联效应呈现先增强后减弱的特征。
(3) 随着主扭平频率比的增大,结构按一阶振型进行动力反应的程度逐渐大于二、三阶振型,结构的动力反应逐渐以一阶振型为主。同时,结构一阶振型由扭转为主逐渐发展为X向平动为主。当结构主扭平频率比Ω1在1附近取值时,一阶振型扭转幅值和平动幅值较为接近,使结构发生较强的平扭耦联反应,扭转效应明显。当Ω1>1时,主方向的平动分量显著增加,远大于扭转分量,振型内的扭转效应减弱。
(4) 在次扭平频率比增大的过程中,结构一、二阶频率的变化较小,且一阶频率值明显大于二、三阶频率值,结构反应以一阶振型为主。结构一阶振型以X向平动为主,并未随Ω2的增加而明显改变。在Ω2变化时,结构的一阶振型始终以平动为主,次扭平频率比的变化对结构平扭耦联效应的影响较小。因此,次扭平频率比对结构扭转的影响要远小于主扭平频率比。
[1] 梁莉军,黄宗明,杨溥. 各国规范关于结构地震下抗扭设计方法的对比[J].重庆建筑大学学报,2002,24(2):52-56.
LIANG Lijun, HUANG Zongming, YANG Pu. The comparison of codes about the method of anti-torsion design under the earthquake[J]. Journal of Chongqing Jianzhu University, 2002,24(2):52-56.
[2] HEJAL R, CHOPRA A K. Earthquake response of torsionally coupled frame buildings[J].Journal of Structural Engineering,1989,115(4):834-851.
[3] TENA-COLUNGA A, ZAMBRANA-ROJAS C. Dynamic torsional amplifications of base-isolated structures with an eccentric isolation system[J]. Engineering Structures, 2006,28:72-83.
[4] TENA-COLUNGA A, ESCAMILLA-CRUZ J L. Torsional amplifiations in asymmetric base-isolated structures[J]. Engineering Structures, 2007,29:237-247.
[5] THAMBIRATNAM K. Simplified procedure for seismic analysis of asymmetric Buildings[J].Computer & Structures,2001, 79:2833-2845.
[6] PETROVCIC K, SILIH K. Seismic analysis of an asymmetric fixed base and base-isolated high-rack steel structure[J]. Engineering Structures, 2011,33:3471-3482.
[7] 邬瑞锋,蔡贤辉,曲乃泗. 多层及高层房屋扭转耦联弹塑性地震反应的研究[J].大连理工大学学报, 1999,39(4):471-477.
WU Ruifeng, CAI Xianhui, QU Naisi. Study on inelastic torsional coupled seismic response of multistory and high rise buildings[J]. Journal of Dalian University of Technology, 1999,39(4):471-477.
[8] 戴君武, 张敏政. 偏心结构扭转振动研究中几个基本参量的讨论[J]. 地震工程与工程震动, 2002,22(6):38-43.
DAI Junwu, ZHANG Minzheng. Discussion on several basic parameters in study of seismic torsional effects of asymmetric structures[J]. Earthquake Engineering and Engineering Vibration, 2002,22(6):38-43.
[9] KYRKOS M T, ANAGNOSTOPOULOS S A. Improved earthquake resistant design of eccentric steel buildings[J]. Soil Dynamics and Earthquake Engineering, 2013,47:144-156.
[10] 建筑抗震设计规范:GB 50011—2010[S]. 北京:中国建筑工业出版社, 2010.
[11] 龙驭球,包世华,匡文起,等. 结构力学Ⅱ—专题教程[M]. 2版.高等教育出版社, 2006:172-173.
Vibration shape influencing parameters of a single-layer bidirectional asymmetric structure
JIANG Xinliang, HAN Yang
(School of Civil Engineering, Tianjin University Key Laboratory of Coastal Civil Engineering Structure and Safety, Ministry of Education, Tianjin 300072, China)
In order to deeply analyze the influence laws of translational-torsion coupled parameters of a single-layer bidirectional asymmetric structure, the dynamic equation of a single-layer bidirectional eccentric structure with 3-DOF was built, the explicit analytical solution to the dynamic characteristics of the single-layer bidirectional eccentric structure was derived using Sheng-jin formula for solving cubic algebraic equations in mathematics. The structural Influencing parameters were extracted according to the form of the explicit solution and determination condition, they were different from those of a one-directional eccentric structure including eccentric distance, eccentric angle, main torsion-translational frequency ratio and minor torsion-translational frequency ratio. According to the explicit analytical solution derived, the structure’s main dynamic characteristics including natural frequencies and modal shapes were obtained. The influence of each parameter on translational-torsion coupled characteristics of the single-layer bidirectional eccentric structure was analyzed. The results showed that the translational-torsion coupled parameters of the bidirectional eccentric structure are similar to those of the one-directional eccentric structure, but those of the former are more complex; they are related to the main torsion-translational frequency ratio and the minor torsion-translational frequency ratio, the influence levels of the two frequency ratios are obviously different.
bidirectional asymmetric structure; analytical solution; influencing parameters; eccentric distance; eccentric angle; torsion-translational frequency ratio
国家自然科学基金资助项目(51278335)
2016-04-05 修改稿收到日期:2016-06-17
姜忻良 男,教授,博士生导师,1951年生
TU311.3
A
10.13465/j.cnki.jvs.2017.15.016
