关于双曲线若干问题的探讨

杨德甘肃省卓尼县柳林中学

关于双曲线若干问题的探讨

杨德
甘肃省卓尼县柳林中学

双曲线是圆锥曲线的重要内容之一，也是高考的热点问题，知识综合程度较高，且易于发散，运算复杂．此中不乏双曲线的第二定义和焦点弦等问题，无疑，这类问题在启迪学生思维，拓宽解题思路等诸多方面都有十分重要的作用，因而它在中学数学教材及各种复习资料中始终占有一席之地，针对双曲线的第二定义、焦点弦等问题及其应用，有必要作进一步的探讨和研究。

新课改；双曲线；焦点弦；第二定义

1 引言

新的数学课程标准是在以学生发展为本的理念下，要求学生转变学习方式，教师积极探索，转变教与学观念，加深对课本内容的拓展理解和应用。所以，在数学教学中，教师应善于引领学生对课本的一些重要问题进行进一步的探索与研究，以提高学生的数学素质与应试能力。

2 双曲线的两个定义

定义1我们把平面内与两个定点F1，F2的距离的差的绝对值等于常数（小于F1F2）的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距。

定义2平面上与一个定点（焦点F）的距离和一条定直线（准线l）的距离的比等于常数e的点的轨迹，当0＜e＜1时是椭圆;当e＞1时是双曲线;当e=1时是抛物线。()

例1已知点P到定点F2c,0的距离和它到定直线l∶x=的距离比是常数(c＞a＞0)，求点P的轨迹。

解设P(x,y)根据题意得：

化简得

令c2-a2=b2，则上式可化为

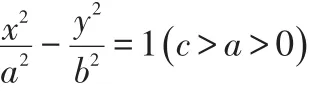
由此得双曲线的标准方程，这个双曲线的离心率就是P到定点F2的距离和它到定直线l（F2不在l上）的距离比。

事实上，在由第一定义推导双曲线标准方程时，曾得到这样一个式子：

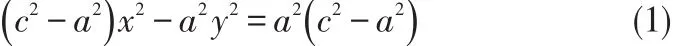
令c2-a2=b2，则上式可化为：

如果对(1)式做如下处理

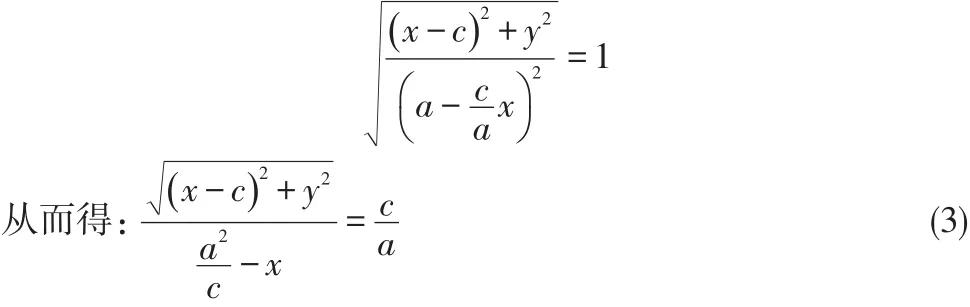
(3)式的几何意义是∶

动点Px,y到定点Fc,0的距离与P到定直线l∶x=的距离的比值是一个常数=e＞1(c＞a＞0)．这正好是双曲线的第二定义，由此可见双曲线的第一、二定义是相互包容的。

3 焦点弦问题

定义3经过圆锥曲线焦点且被圆锥曲线截得的线段叫做焦点弦。

这是一个非常重要的几何量，在历次考试中出现频率较大，且形式多样。

过双曲线焦点F且与该双曲线交于A，B两点，倾斜角为α，则有

(1)当直线l与双曲线的两个交点A，B在双曲线的同支上时，

(2)当直线l与双曲线的两个交点A，B在双曲线的异支上时，

(3)当直线l与双曲线只有一个交点时，

证明由对称性，不妨设F为有焦点(c,0)

(1)由渐近线与弦AB斜率的关系知

(2)首先A，B在双曲异支上时，由渐近线与弦AB斜率的关系知

(3)由于直线l与双曲线有且只有一个交点，依题意则直线l与该双曲线的渐近线平行，即

对焦点在y轴上的双曲线而言，也有上述性质。

[1]陈炆.圆锥曲线统一定义与统一方程中若干问题释疑[J].数学通讯，2010(12)∶10-12.

[2]巨鹏，孙月芳.圆锥曲线焦点弦长的公式求法[J].内江科技，2010(5)∶31-32.

[3]彭世金.圆锥曲线焦点弦长的一个公式及应用[J].数学通讯，2007(22)∶22-23.

杨德，中学一级教师，现任甘肃省卓尼县柳林中学政教处主任。