海底多段悬跨管道涡激振动特性分析

徐万海，谢武德，高喜峰，马烨璇

（天津大学水利工程仿真与安全国家重点实验室，天津300072）

海底多段悬跨管道涡激振动特性分析

徐万海，谢武德，高喜峰，马烨璇

（天津大学水利工程仿真与安全国家重点实验室，天津300072）

深海海底多跨管道相比于单跨，其涡激振动行为却更为复杂。文章考虑了两端跨肩和中间支撑处的管—土作用边界条件，提出了多跨管道涡激振动预报模型，标定了模型参数，并重点分析了跨肩边界条件、中间支撑条件和悬跨长度对管道涡激振动特性的影响。结果表明：较大的两端边界处扭转弹簧弹性系数、较大的中间支撑处扭转和拉伸弹簧弹性系数和较短的悬跨长度，会限制管道结构高阶模态的激发，同时还发现了振动能量会在相邻管跨之间传递的现象。

海底管道；流—固耦合；涡激振动；多跨

0 引言

海底管道是深海油气开采输运不可或缺的关键设备。由于深海海底地形复杂，地势大量起伏，加之海流冲刷作用，直接铺设于海底的管道频繁出现悬跨，由此引发的悬跨管段涡激振动是导致管道结构疲劳损伤的重要因素[1]。

长期以来，人们更多地关注单跨管道涡激振动问题[2-4]，缺乏对多跨管道涡激振动的深入研究。与单跨管道相比，多跨管道的边界条件更加复杂、振动常呈现多模态、危险性更高等特点。近期，挪威的MARINTEK机构研究了多跨单模态和多跨多模态的涡激振动特性，采用特殊弹簧装置近似两端跨肩处的土体边界对管道作用[5-6]，部分实验成果反映在最新推荐的海底管道设计规范DNV-RP-F105[7]上。李明明[8]数值模拟了跨肩长度、土体性质等因素对悬跨管段振动固有频率的影响，并对深海多跨管道VIV疲劳进行了评估。Soni[9]通过特殊的弹簧装置实验模拟相邻管跨之间的土体支撑，观测了多跨管道邻近跨间的相互作用。Koushan[10]在深入研究多段悬跨海底管道涡激振动后指出：准确地分析自由管跨段VIV，必须合理简化跨肩处的土体边界和多跨管道的相邻跨间影响机制等。

现阶段，学术界和工程界对海底多跨悬空管道涡激振动问题的认识水平还无法满足深海工程实际需求。本文首次提出多跨管道涡激振动的预报模型，并讨论多跨管道两端跨肩边界、中间支撑条件和相邻管跨段长度等因素对涡激振动特性的影响机制。

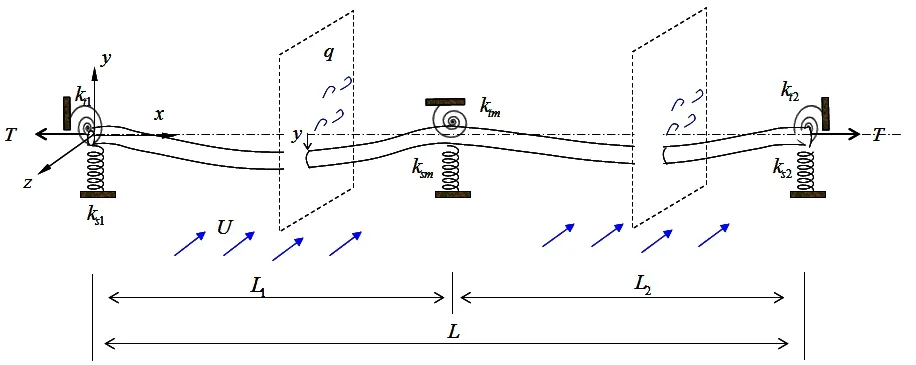
图1 多跨管道示意图Fig.1 Multi-span pipelines

1 数学模型

1.1 管道结构方程

本文研究垂直来流方向上的横流向涡激振动，忽略管道的几何非线性和水动力对跨肩处管段的影响，如图1所示的多段悬跨管道能够简化为欧拉-伯努利梁，管道的左端取为直角坐标系原点，结构的控制方程如下：

式中：m=ms+ma，ms为单位长度结构质量，ma（=CaπρD2/4）为附加质量，Ca是附加质量系数，D为管道的外径，ρ为海水密度，y为横流向的结构位移，t为时间，C=Cs+Cf为管道的阻尼（包括结构阻尼Cs和水动力阻尼Cf），T为管道轴向力，x为管道轴向的空间坐标，EI为结构的弯曲刚度，FL（=CLρDU2/2）是漩涡脱落引发的涡升力，CL为瞬时的升力系数，U为海流速度。

1.2 尾流振子方程

海流流经悬跨管段时，会诱发交替的漩涡脱落，工程上常采用尾流振子模型分析尾流与结构的相互作用，运用Van der pol方程描述漩涡脱落的尾迹特性。Facchinetti[11]提出了加速度耦合尾流振子模型，可很好地描述海底管道涡激振动这种流-固耦合问题，模型方程如下：

式中：变量q表示瞬时的升力系数CL与固定圆柱升力系数CL0之比，q=2CL/CL0，ωs（=2πStU/D）为漩涡脱落频率，其中St是Strouhal常数。ε和A为尾流振子的模型参数，根据漩涡脱落的情况而选取不同的数值，它反映了尾流振子模型和管道涡激振动的耦合关系。徐万海等[12]对尾流振子的模型参数进行了修定，弥补了Facchinetti模型仅能定性不能定量预报涡激振动的不足。当约化速度Vr（=2πU/（ωnD）），ωn为管道结构的圆频率)处于不同范围时，参数A的取值为[12]：

根据管道的最大响应幅值与实验值相等的原则，确定模型参数ε，如下：

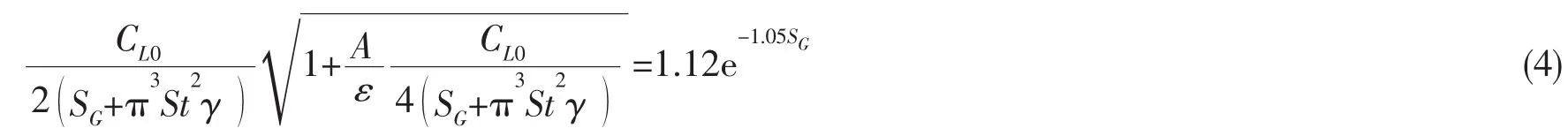
式中：SG为约化质量阻尼参数：

γ为迟滞因子，表达式为：

ζ为结构阻尼因子，CD为阻力系数，综合利用（3）-（6）式，最终确定ε和A值。本文采用上述尾流振子模型描述漩涡脱落与管道结构之间的流-固耦合作用。

1.3 两端跨肩和中间支撑处的边界条件

土壤的性质、管土相互作用长度、管线掩埋深度和管线掩埋宽度对海底悬跨管道的涡激振动都有很大的影响。根据海底管线的实际情况，DNV-RP-F105[7]将端部跨肩处管土相互作用土壤分成了多个等级。工程界为了简化分析过程，常将悬跨管道两端约束简化为简支边界或者固支边界。实际上，两端跨肩处的约束条件一般介于简支状态和固支状态之间。因此，跨肩边界可等效为弹性支承，以扭转弹簧和拉伸弹簧约束模拟工程实际中的管土相互作用，假设海床水平，边界条件方程为[13]：

其中：kt1和ks1分别为悬跨管道左端扭转和拉伸弹簧弹性系数，kt2和ks2为右端扭转和拉伸弹簧弹性系数，L=L1+L2，为悬跨管道的整体长度。

中间支撑部分近似为弹性支撑，ktm和ksm为支撑处的扭转和拉伸弹簧弹性系数，并且在中间支撑处约束满足悬跨L1和L2在连接处的位移、转角、剪力和弯矩相等[14]，如下所示：

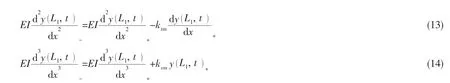
其中：下角标“-”表示中间支撑处的左侧，“+”表示中间支撑处的右侧。

2 数值求解方法

本文以两跨管道为例，设管道的振型函数为：

其中：φ1（x）是管道第一跨的振型函数，φ2（x）是管道第二跨的振型函数，即：

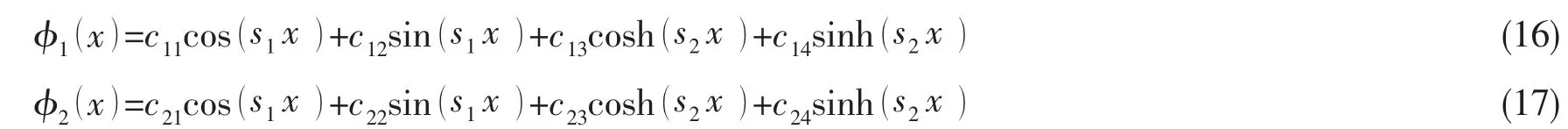
cij（i=1,2;j=1,2…4）是待求系数。

根据悬跨管道两端边界条件，以及中间支撑条件，可获得管道的振型函数。运用模态展开法，分析悬跨管道的涡激振动特性，令：

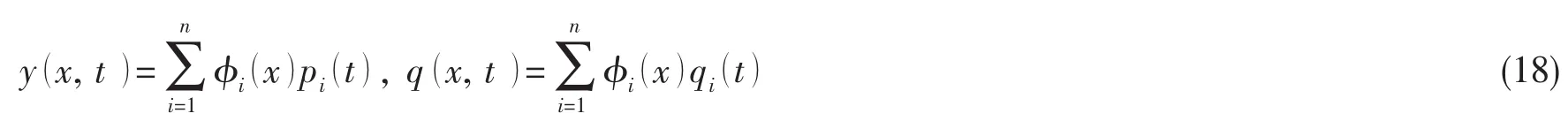
将（18）式代入（1）和（2）式，根据振型正交性，对方程进行化简：

3 模型正确性验证

采用四阶龙格-库塔法对方程组（19）和（20）进行数值求解。海底悬跨管道涡激振动一般较难出现高阶模态，因此仅取前四阶模态（n=4）分析，即可得到合理结果。为了验证多跨管道涡激振动尾流振子模型的合理性，以及数值算法的正确性，首先以MARINTEK的Koushan实验（如图2所示）[10]为算例，进行分析验证。实验中两段悬跨管道长度相等，为4.126 m，管道外径为0.035 11 m，模型的其它参数：轴向张力为50 N，单位长度质量为1.307 kg/m，弯曲刚度EI=203 Nm2。图3对比了管道结构的最大响应幅值计算结果与实验结果，DNV规范结果，以及涡激振动计算软件VIVANA的模拟结果，通过分析可以发现：较低的流速条件下，多跨管道一阶模态被激发，随着流速增大，二阶、三阶模态相继被激发，本文的预报模型计算结果比DNV规范略小，比VIVANA软件结果稍大。计算过程中第四阶模态一直未被激发，也充分证明了取前四阶模态进行分析的合理性。模型预报结果在较低流速条件下与实验结果十分接近，但较高流速时，产生了一定差异，主要原因是MARINTEK的管道模型轴向力是在静水条件下施加的，但实验过程中，随着外部来流速度的增大，管道模型产生了一定的挠曲变形，直接导致轴向力大幅增加，而本文模型分析的轴向力取值相对偏小，导致了预报结果大于实验观测结果，但是整体的变化趋势比较接近。所以，从整体分析结果判断，该涡激振动预报模型的正确性和适用性是可以保证的。

图2 MARINTEK实验装置示意图Fig.2 Sketch of the experimental apparatus in MARINTEK

4 多跨管道涡激振动特性分析

本部分重点分析跨肩边界条件、中间支撑条件和不同管跨的悬跨长度等对多跨管道涡激振动特性的影响，选择实际工程中最常见的两跨管道作为分析对象，基本的计算参数如表1所示。外部来流速度根据实际海流速度，选为0.4-3.5 m/s之间，并假定两端跨肩处具有对称的边界条件（kt1=kt2=kt；ks1= ks2=ks）。

图3 最大响应幅值结果对比结果Fig.3 Comparison of the results on maximum response amplitude

4.1 端部边界条件影响

首先研究跨肩处拉伸弹簧系数足够大（ks= 1010），扭转弹簧系数变化时（kt=0、102、104、106、108和1010），讨论其对海底两跨管线涡激振动的最大响应振幅和频率的影响，中间支撑假定为简支（ktm= 1010，krm=0），令第一跨的悬跨长度为80 m，第二跨的悬跨长度为60 m。改变两端扭转弹簧弹性系数，模拟两端边界从简支变化到固支的全过程。

图4和图5分别给出了扭转弹簧弹性系数变化时，不同悬跨段管道结构的响应幅值和响应频率。从图4（a）中可以看出随着扭转弹簧弹性系数增加，最大响应幅值曲线的峰值几乎没有发生改变，仅是整体向右移动，扭转弹簧弹性系数在0-106区间范围时，扭转弹簧对悬跨段L1的涡激振动影响很小；弹性系数介于106-1010时，弹性系数越大，悬跨段L1的响应幅值就越小，对响应幅值曲线的峰值影响不明显。图4（b）中有关L2管跨段最大响应幅值结果与L1段相似，其结论也相似。对比图4（a）和图4（b）能够发现，L1管跨段结构响应幅值获得极大值时，L2管跨段会出现极小值，反之亦然，这充分地证明了涡激振动能量存在在相邻管跨之间的实时传递的现象。从图5（a）中能够得到扭转弹簧系数在0-106时，其对悬跨段L1的涡激振动响应频率几乎没有影响；扭转弹簧系数在106-1010时，扭转弹簧系数越大，悬跨段L1的涡激振动响应频率就越大，高阶模态也越难被激发。图5（b）中的L2有相似结果。

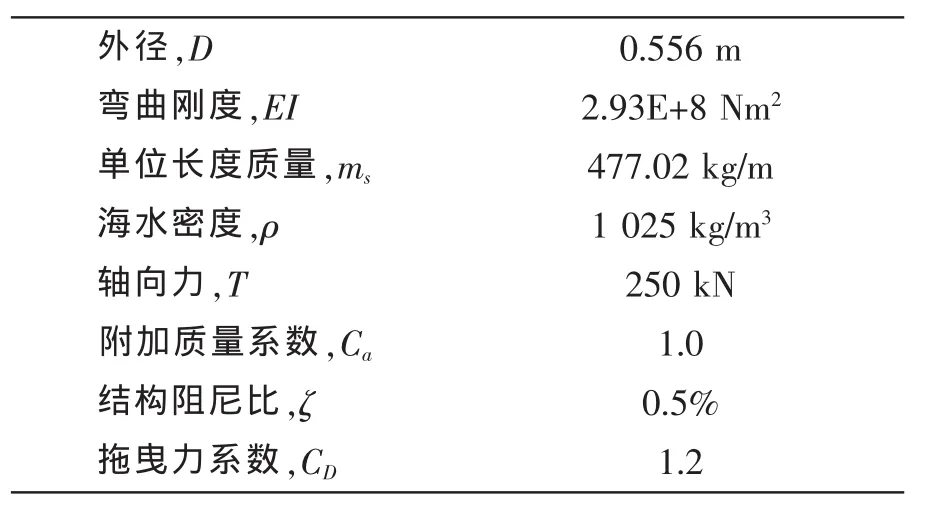
表1 计算模型参数[10]Tab.1 Base set of system parameters[10]

图4 扭转弹簧弹性系数变化时，不同管跨的响应幅值Fig.4 Response amplitudes of different spans with torsional spring stiffness

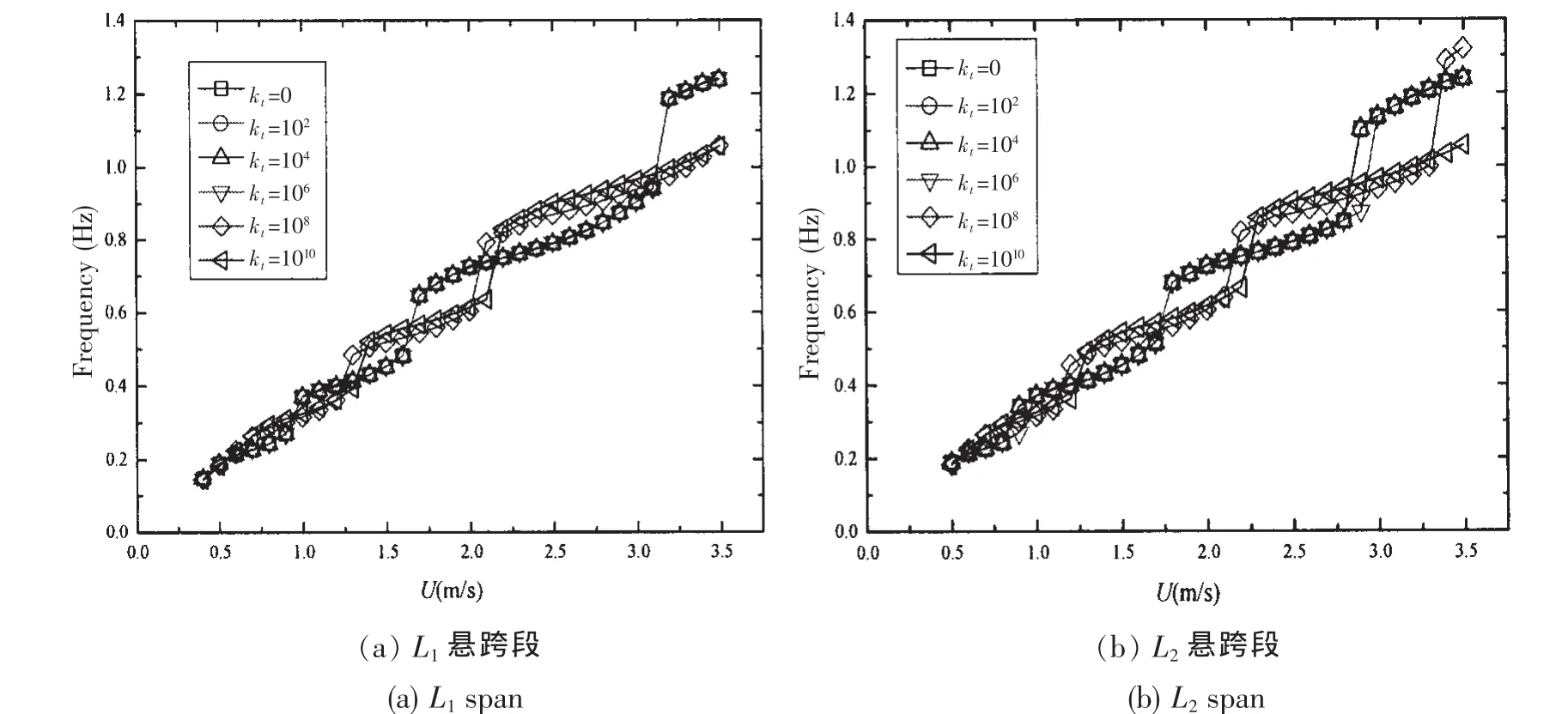
图5 扭转弹簧弹性系数变化时，不同管跨的响应频率Fig.5 Response frequencies of different spans with torsional spring stiffness

4.2 中间支撑条件影响

海底多跨管道中间一般是由土壤进行支撑的，扭转弹簧和拉伸弹簧常被用来模拟中间支撑处的管土相互作用，在此，重点分析多跨管道中间支撑处扭转弹簧和拉伸弹簧对两跨管线涡激振动的影响。为了简化起见，将两端设定为简支边界。仍假设第一跨的悬跨长度为80 m，第二跨的悬跨长度为60 m。

4.2.1 中间扭转弹簧

固定中间支撑处的拉伸弹簧系数（设为ksm=1010），变化中间扭转弹簧系数（ktm=0、102、104、106、108和1010）。计算涡激振动响应的最大响应振幅和响应频率，如图6和图7所示。

图6 中间支撑处扭转弹簧弹性系数变化时，不同管跨的响应幅值Fig.6 Response amplitudes of different spans with torsional spring stiffness at the middle support

图7 中间支撑处扭转弹簧弹性系数变化时，不同管跨的响应频率Fig.7 Response frequencies of different spans with torsional spring stiffness at the middle support

分析图6（a）最大响应幅值，扭转弹簧系数处于0-106范围内时，最大振幅响应曲线几乎重合。扭转弹簧系数介于106-108之间时，随着中间扭转弹簧系数的增加，L1的响应幅值减小，而且整个振幅曲线向右移动。这说明：扭转弹簧系数在0-106时，中间扭转弹簧系数对悬跨段L1涡激振动最大响应幅值几乎没有影响；扭转弹簧系数在106-1010时，中间扭转弹簧系数越大，L1涡激振动响应幅值就越小，高阶模态激发就越困难。对于L2跨管道，图6（b）的结果与图6（a）大致相同。

图7（a）给出了中间不同扭转弹簧系数，不同来流速度下，L1管跨段的响应频率。从图中可以得到：扭转弹簧系数在0-106时，悬跨段L1的响应频率曲线重合；扭转弹簧系数在106-1010时，随着中间扭转弹簧系数的增加，悬跨段L1的响应频率略有增加。随着来流速度的增加，较小的扭转弹簧系数会提前激发高阶振型。L2跨管道具有与L1跨管相近的特性，如图7（b）所示。

4.2.2 中间拉伸弹簧

进一步分析中间拉伸弹簧对悬跨管线涡激振动响应的影响。设定两端为简支边界，固定中间支撑处的扭转弹簧系数（设为ktm=0），变化中间拉伸弹簧系数（ksm=0、102、104、106、108和1010）。计算两跨管线涡激振动响应的最大振幅和频率，如图8和图9所示。

图8 中间支撑处线弹性弹簧弹性系数变化时，不同管跨的响应幅值Fig.8 Response amplitudes of different spans with stretching spring stiffness at the middle support

图9 中间支撑处线弹性弹簧弹性系数变化时，不同管跨的响应频率Fig.9 Response frequencies of different spans with stretching spring stiffness at the middle support

根据图8（a）中悬跨段L1最大响应幅值可发现，随着中间支撑处拉伸弹簧弹性系数增加，最大响应幅值曲线整体右移。同时明显区分为三个振动状态，中间支撑拉伸弹簧的弹簧系数介于0-104、108-1010之间时，响应幅值近似相同，而在104-108的过渡区间段，曲线产生了明显的分离。图8（b）中的悬跨段L2具有相似的结论。

图9中两组曲线的总体走势基本相同，拉伸弹簧系数在0-104时，响应频率曲线几乎重合，拉伸弹簧系数在108-1010时，响应频率曲线也十分接近，但是不同于过渡区间的情形。

4.3 悬跨长度的影响

悬跨长度是影响海底管道涡激振动特性的重要因素，尤其对于多跨管道。相邻管跨之间、悬跨跨长对管道涡激振动影响机制尚不清晰。在此，悬跨段L1长度设定为80 m，变化悬跨段L2的长度（取为40、60、80和100m），探讨研究悬跨长度对两跨管道涡激振动的影响。绘制涡激振动响应最大响应幅值和频率图像，如图10和图11所示。

分析图10（a）中的悬跨段L1最大响应幅值可知，随着悬跨段L2长度的增加，响应幅值略有增加，曲线波谷和波峰都有向左移动的趋势。这表明：悬跨段L2越长，悬跨段L1的涡激振动响应幅值就越大，而且越容易激发高阶模态。图10（b）中悬跨段L2最大响应幅值与图10（a）中悬跨段L1最大响应幅值有明显的不同。随着悬跨段L2长度的增加，最大响应幅值曲线向左移动，峰值和谷值逐渐增加。这说明悬跨段L2越长，其涡激振动响应幅值就越大，而且高阶模态容易被激发。

图10 整体悬跨长度变化时，不同管跨的响应幅值Fig.10 Response amplitudes of different spans with the whole spanning length of pipeline

图11 整体悬跨长度变化时，不同管跨的响应频率Fig.11 Response frequencies of different spans with the whole spanning length of pipeline

图11（a）悬跨段L1响应频率可以发现相同外界流速的情况下，随着悬跨段L2的增加，悬跨段L1的响应频率逐渐降低；模态竞争区域向左移动。这表明：悬跨段L2长度越长，悬跨段L1的响应频率就越大，越容易进入模态竞争区域，越容易激发高阶模态。图11（b）中悬跨段L2响应频率和图11（a）悬跨段L1响应频率具有相同的现象和相似的结论。

5 结论

针对海底多跨悬空管道横流向涡激振动问题，本文提出了适用于多跨管道涡激振动预报的尾流振子模型，通过将模型预报结果与DNV规范、VIVANA数值模拟和实验结果的对比，验证了该模型的适用性和精确性。运用该模型，分析了多跨管道的跨肩边界条件、中间支撑条件以及悬跨长度对涡激振动的影响机制，通过对比分析最大响应幅值和响应频率，可发现：

（1）两端边界处的扭转弹簧弹性系数较低时，对多跨管道悬跨段的涡激振动几乎没有影响；但随着弹性系数的增加，影响逐渐凸显，悬跨段的最大响应幅值会略微变小，响应频率会增加，高阶模态被激发的难度变大。同时证实了涡激振动的能量会在相邻管跨之间传递。

（2）中间支撑处的扭转弹簧弹性系数处于较低区间范围时，对多跨管道涡激振动的最大响应幅值和响应频率几乎都没有影响；较高的扭转弹簧弹性系数会让中间支撑处的约束增强，导致高阶模态不容易出现；中间支撑处的拉伸弹簧也可以得到类似的结论。

（3）随着悬跨长度增加，多跨管道最大响应幅值会增加，响应频率亦会增加，容易激发高阶模态，也容易进入模态竞争区域。

[1]Bai Yong,Bai Qiang.Subsea pipelines and risers[M].Elsevier Science Ltd,2005.

[2]吴钰骅,金伟良,龚顺风,等.海底管道流固耦合振动数值模拟[J].浙江大学学报（工学版）,2009,43(4):782-788. Wu Yuhua,Jin Weiliang,Gong Shunfeng,et al.Submarine pipeline vibration considering fluid-structure interaction[J]. Journal of Zhejiang University(Engineering Science),2009,43(4):782-788.(in Chinese)

[3]Srinil N,Zanganeh H.Modelling of coupled cross-flow/in-line vortex-induced vibrations using double Duffing and van der Pol oscillators[J].Ocean Engineering,2012,53:83-97.

[4]李小超,王永学,王国玉，等.固定海床上海底管跨顺向和横向耦合振动实验研究[J].船舶力学,2013,17(5):547-558. Li Xiaochao,Wang Yongxue,Wang Guoyu,et al.Experimental investigation of in-line and cross-flow VIV of free spans near a plane boundary[J].Journal of Ship Mechanics,2013,17(5):547-558.(in Chinese)

[5]Nielsen F G,Soreide H T,Kvarme S O.VIV response of long free spanning pipelines[C]//The 21st International Conference on Offshore Mechanics and Arctic Engineering,OMAE.Oslo,Norway,2002.

[6]Soreide T H,Ilstad T,Paulsen G,Nielsen F G.Dynamic response of pipeline in long free spans or multi-spans[C]//The Sixth European Conference on Structural Dynamics,EURODYN.Paris,France,2005.

[7]DNV-RP-F105.Free spanning pipelines[M].HΦvik.Det Norske Veritas,2006.

[8]李明明.深水多跨管道VIV疲劳评估[D].哈尔滨:哈尔滨工程大学,2011. Li Mingming.VIV fatigue assessment of deepwater multi-span pipeline[D].Harbin:Harbin Engineering University,2011. (in Chinese)

[9]Soni P K.Hydrodynamic coefficients for vortex-induced vibrations of flexible beams[D].Norwegian:Norwegian University of Science and Technology(NTNU),2008.

[10]Koushan K.Vortex induced vibrations of free span pipelines[D].Norwegian:Norwegian University of Science and Technology(NTNU),2009.

[11]Facchinetti M L,Langre E,de Biolley F.Coupling of structure and wake oscillators in vortex-induced vibrations[J].Journal of Fluids and Structures,2004,19(2):123-140.

[12]Xü Wanhai,Wu Yingxiang,Zeng Xiaohui,Zhong Xingfu,Yü Jianxing.A new wake oscillator model for predicting vortex induced vibration of a circular cylinder[J].Journal of Hydrodynamics,Ser.B,2010,22(3):381-386.

[13]Bakhtiary AY,Ghaheri A,Valipour R.Analysis of offshore pipeline allowable free span length[J].International Journal of Civil Engineering,2007,5(1):84-91.

[14]Motaghian S E,Mofid M,Alanjari P.Exact solution to free vibration of beams partially supported by an elastic foundation [J].ScientiaIranica,2011,18(4):861-866.

Study on Vortex-Induced Vibrations(VIV)of multi-spans pipelines

XÜ Wan-hai,XIE Wu-de,GAO Xi-feng,MA Ye-xüan
(State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072)

Multi-spans submarine pipelines are more normal than single-span ones at the bottom of deep sea.And their VIV characteristics are more complex.In this paper,the boundary condition in shoulders and pipe-soil interaction at the middle support were considered.A wake oscillator model for VIV prediction of multi-spans pipelines was introduced,and the model parameters were estimated.The influence of multispans length and boundary conditions in shoulders and middle support on the VIV of pipelines was analyzed.The results indicates that increasing the torsional spring stiffness and stretching spring stiffness may limit the occurrence of high mode,increasing the length of multi-spans submarine pipelines may cause high mode to easily happen.And it was also found that the energy could pass through the neighbor spans when the pipeline was suffered from VIV.

submarine pipelines;interaction of fluid and structure;Vortex-Induced Vibrations(VIV); multi-spans

TV312

A

10.3969/j.issn.1007-7294.2017.08.012

1007-7294（2017）08-1025-10

2016-12-28

国家自然科学基金（51209161、51379144、51479135、51679167）；国家自然科学基金创新研究群体科学基金（51621092）；国家重点基础研究计划-973计划（2014CB046801）

徐万海（1981-），男，副教授，硕士生导师，E-mail:xuwanhai@tju.edu.cn；谢武德（1989-），男，博士研究生，E-mail:tjuxwd@126.com。