关于圆柱体积的推导

古丽披扎木·吐尔逊

在小学的教学和学习的过程中，大部分的数学公式都是通过一步又一步的推导得来的，特别是在求几何图形的面积、立体几何的体积的时候，都是将许多未知的量设为已知，将许多陌生的量转变为熟悉的量，让学生在轻松的学习中获得了新的知识，培养了学生的创新意识和实践能力. 下面就圆柱体积教学来简单说下我的观点：

关于圆柱的知识是小学课本中最重要的比较复杂的知识之一，圆柱实际应用是挺广泛的立体图形，它给学生带来了很大的想象空间和培养逻辑思维能力并解决实际问题的能力。

新编的十二册数学教材内容是相当详细，虽然科学理论知识和实际问题协调制定的，但是课本中的圆柱体积知识在课堂教学中缺乏使用教学工具的便利，这影响学生的解决实际问题能力和思维想象能力。

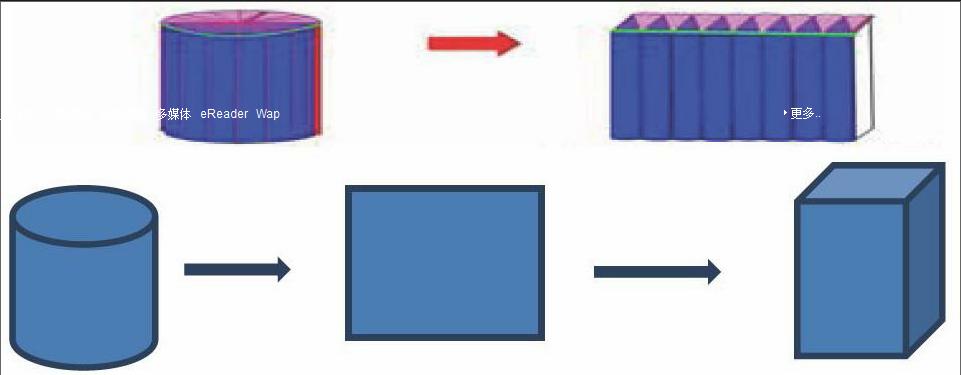
我们先谈谈本课时的内容：能否把圆柱转化成我们学过立体图形来计算它的体积。教材上指出的计算圆柱体积的方法：把圆柱的底面切成许多形状相同、大小相等的立体图形，然后把它拼成右边的图形。

拼成的扇形所拼成的图形与长方体十分相似，分成的块数越多，所拼成的图形越接近长方体。拼成的长方体底面积与圆柱底面积S相等，高度与等于圆柱的高度h，长方体的体积等于底面积乘高，所以圆柱的体积计算公式为V=Sh，此方法虽然正确，但是我们的数学教学实践条件和同学们的想象能力是有限的。

一、我们利用教学工具让学生掌握转换思想本质，有利于正确理解圆柱体实际问题，在课堂教学中这种方法基本从理论方面了解，但是学生需要从本质上理解。

二、用这种方法教学时，具体的概念会变成抽象的概念，而学生从实践理解问题的能力得不到明显的效果。学生只有形成关于公式的规范形式来解决问题的能力。

三、圆柱的底面是圆形的，把圆柱分成许多相等的扇形所拼成的圆形的底面是长方形，比较周长相等圆形和长方形的面积，有相当大的区别。再说所拼成的图形的底面周长，等于许多相等的小扇形弧长相连所成的，比原来圆柱底面周长的小。由于这个原因学生想象中（高相等时）底面周长间的区别较大，所以对它们的体积相等，学生疑惑较低，容易给他们留下疑知。

我们在课本中推出圆柱体积計算公式是，把圆柱分割拼折成对应状态的长方体。长方体的底面为正方形或长方形。

在平面图形中比较周长相等的圆，长方形，正方形的面积。

长方形的面积<正方形的面积<圆的面积

所以要得出圆柱体积的计算方法规则，把它化作底面为正方形的长方体。可以让学生记住难点，理解重点和实践运用公式方面在课堂中用教学工具来取得一定的成绩，用这种方法来教学的方法是这样的：

先用一个长方形纸片拼折转化成一个圆柱，然后在课堂中把它的相反面合成一块，并排折叠做出一个长方形等于原长方形的一半，然后把它展开把折过的两边放一块再折一遍。然后把它展开就能得到周长（底边）与原来一样底边为正方形的一个长方体。

用这种方法把圆柱变成长方体时，它底面的周长与高不变，误差就会最小。现在把这个圆柱的体积算出来：这个长方体底面面积等于圆柱底面的面积S，高等于圆柱的高h，因为长方体的体积等于底面积乘高，所以圆柱的体积计算公式为V=Sh。用这种方法推出圆柱的体积公式时，一边思维上的误差基本解除，另一边课堂知识可以有目标性的按照适合目前的素质教育要求，升华学生对立体图形的认识，提高学生对立体图形的观察、想象能力。增强教学内容的实用性、实践性。总之，为了让学生能轻松愉快的学，积极主动探索，根据学生的实情，我主要选用自主观察，自主探索，合作交流，直观演示等方式为主，再加上老师的适时点拔，学生间的互相补充，评价等方式为铺，完成教学目标。一节课即将结束时，老师引导学生回顾圆柱体积的简便计算方法的过程，计算时运用数学的思想，使学生学习计算中，不仅有知识上的累积，还能在学习计算方法上有很多收获，使学生感受到学习数学的快乐和价值。

总而言之，教会学生们自己独自解决问题，对学生们是个挑战，对老师们也是一个巨大的挑战，老师们不仅仅要有自己的教学风格，还要有自己的教学手段，鼓励孩子们勇于尝试，勇于创新，不要害怕失败，也不要对知识存在畏惧的心理，只有战胜这些，学生们才会更有兴趣和信心继续学习. 与此同时，也要加强他们创新的能力，鼓励他们有自己的思维方式和解题策略，不要将学生的思维固定，让学生拥有的不是老师传授的经验，而是自己总结得到的经验。