一道高考题解法的探究与推广

安徽省灵璧中学 侯立刚 (邮编:234200)

一道高考题解法的探究与推广

安徽省灵璧中学 侯立刚 (邮编:234200)

(1)求C的方程;

(2)设直线l不经过P2点且与C相交于A, B两点.若直线P2A与直线P2B的斜率的和为－1,证明:l过定点.

(2)思路一 当直线l的斜率不存在时,设l的方程为x＝m,A(m,yA),B(m,－yA)

当直线l的斜率存在时,设l的方程为y＝kx＋b(b≠1)

(1＋4k2)x2＋8kbx＋4b2－4＝0.

当△＝16(4k2－b2＋1)＞0时,方程有两个不相等的实数根.

设A(x1,y1),B(x2,y2),则x1＋x2＝

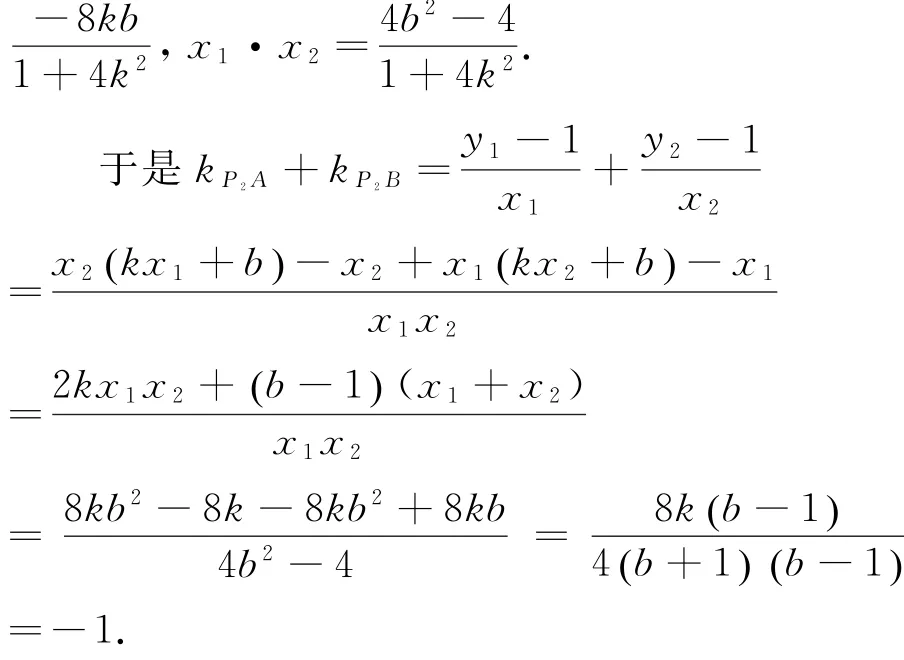
又b≠1,所以b＝－2k－1,此时△＝－64k,存在k使得△＞0成立.

所以直线l的方程为y＝kx－2k－1,即y＝k(x－2)－1.当x＝2时,y＝－1.

所以直线l过定点(2,－1).

思路二 分别设直线P2A、P2B的斜率为k1、k2,则k1≠k2且k1＋k2＝－1.

于是P2A:y＝k1x＋1,P2B:y＝k2x＋1.

当x＝2时,y＝－1,所以直线l过定点2,－1

().

注 这种思路也很自然,不需要讨论直线AB的斜率,但是对运算要求较高,原因是直线P2A,P2B的方程中含有常数项.如果进行坐标平移,便可以把定点P2变换到原点,并且不改变直线的斜率.

设直线l的方程变成l′:mx′＋ny′＝1②

所以2m＝2n＋1,代入直线mx′＋ny′＝1得2n(x′＋y′)＋x′－2＝0.

探究一 此命题的逆命题是否成立?

(1)过(2,－1)的直线斜率不存在时,直线l与椭圆只有一个公共点,不合题意.

(2)当直线l的斜率存在时,设l的方程为y＋1＝k(x－2),即y＝kx＋b(b＝－2k－1≠1).

(1＋4k2)x2＋8kbx＋4b2－4＝0.

当△＝16(4k2－b2＋1)＞0时,方程有两个不相等的实数根,

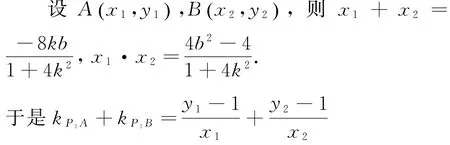
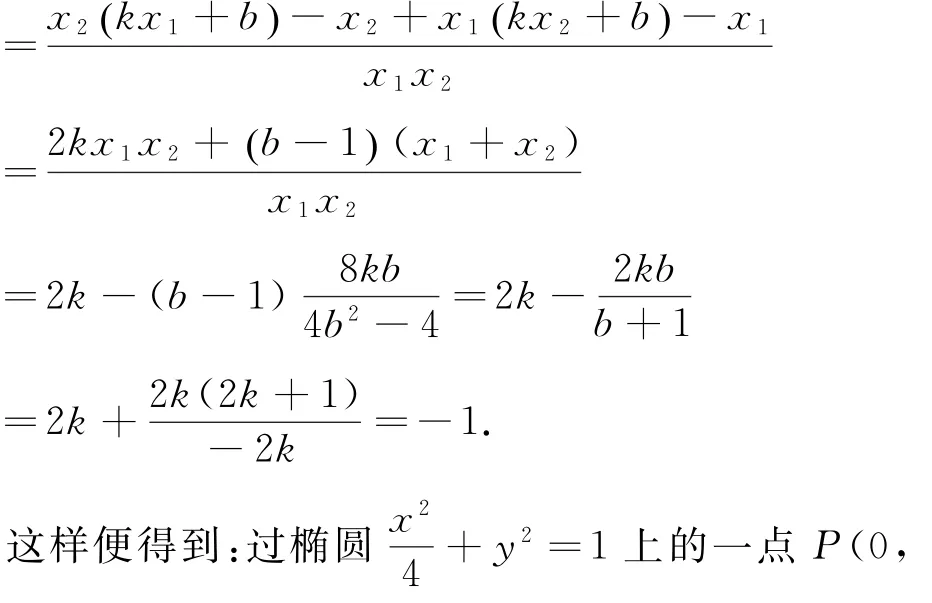
1)作两条直线分别与椭圆交于A,B两点,则

kPA＋kPB＝－1的充要条件是直线AB过定点(2,－1)

显然,当λ＝0时,由椭圆的对称性知,直线AB平行于x轴,不能过定点;

直线AB的方程设为A′B′:mx′＋ny′＝1