一个经典不等式的证法探究

湖南省会同县第一中学 于先金 黄为公 (邮编:418300)

一个经典不等式的证法探究

湖南省会同县第一中学 于先金 黄为公 (邮编:418300)

已知a、b、c＞0,那么a3＋b3＋c3≥3abc①

当且仅当a＝b＝c时,等号成立.

这是人教版选修4－5《不等式选讲》第8页中的一个经典不等式,教材中所给出的证明是比差法,即作差——变形——定号.但为了达到定号的目的而进行因式分解时,在恒等变形过程中用到了公式(x＋y)3＝x3＋3x2y＋3xy2＋y3与x3＋y3＝(x＋y)(x2－xy＋y2),并且把a2＋b2＋c2－ab－bc－ca配凑成了三个平方和整个证明过程确实难度大,技巧要求高,学生不易成功.笔者通过探究和教学实践,得到了一些思路自然.学生易于接受的证法,供参考.

为便于比较,现将教材中的证明作为证法1抄录如下:

证法1 作差比较,恒等变形

因为a3＋b3＋c3－3abc＝(a＋b)3＋c3－3a2b－3ab2－3abc＝(a＋b＋c)[(a＋b)2－(a＋b)c＋c2]－3ab(a＋b＋c)＝(a＋b＋c)(a2＋＋(b－c)2＋(c－a)2]≥0,

所以a3＋b3＋c3≥3abc.

当且仅当a＝b＝c时,等号成立(等号成立的条件以下略).对不等式①的证明,关键是应该以二元均值不等式(a、b＞0)为基础,所以现在面临以下三个问题:第一,把三元转化为二元,所以需添加一项;第二,添加怎样一项?根据不等式①的结构特点,首先考虑的应为ka3、kb3、kc3、kabc(k∈N∗);第三,由不等式取等号时各项相等,因此所添项系数必须为1.经验证,添加a3、b3、c3都不行,而添加abc后,用两次二元均值不等式,正数abc的系数为4,移项后就是要证的不等式①.这样,因为添加一项abc,使不等式①的证明变得出乎意料的简单.

证法2 添加一项,奇异突变

因为a3＋b3＋c3＋abc≥2＋4abc,所以a3＋b3＋c3≥3abc.

教材第21页用作差法很容易证明了这样一个例题:已知a、b、c都是正数,且a≠b,求证

a3＋b3＞a2b＋ab2②

于是,我们自然会考虑是否能用不等式②来证明不等式①,事实上是可行的,而且很简单.

证法3 应用例题,精彩纷呈

因为a3＋b3－(a2b＋ab2)＝(a3－a2b)－(ab2－b3)＝a2(a－b)－b2(a－b)＝(a－b)(a2－b2)＝(a－b)2(a＋b)≥0,所以a3＋b3≥a2b＋ab2.

同理b3＋c3≥b2c＋bc2,c3＋a3≥c2a＋ca2.

三个不等式相加得

2(a3＋b3＋c3)≥a(b2＋c2)＋b(a2＋c2)＋c(a2＋b2)≥a·2bc＋b·2ac＋c·2ab＝6abc,

所以a3＋b3＋c3≥3abc.证法4 作差比较,均值放缩因为 a3＋b3＋c3－3abc＝a(a2－bc)＋2b3＋2c3－ab2－ac2－ba2－bc2－ca2－cb2),以下同证法3.

证法5 二元入手,展开成功

因为 a2＋b2≥2ab,b2＋c2≥2bc,c2＋a2≥2ca,三个不等式相加并除以2得

a2＋b2＋c2≥ab＋bc＋ca③

因为a、b、c＞0,所以a＋b＋c＞0,不等式③两边同乘以a＋b＋c得

(a＋b＋c)(a2＋b2＋c2)≥(a＋b＋c)(ab＋bc＋ca).

两边展开并整理即可得

《中国造纸学报》是由中国造纸学会主办、中国制浆造纸研究院承办的造纸专业学术性期刊，创刊于1986年。主要刊登造纸专业研究论文、学术报告及综合性学术评述，反映我国造纸工业在原材料、制浆、造纸、废液综合利用及污染防治、机械设备、分析检验、工艺和质量控制自动化以及制浆造纸专业基础理论等方面的新进展和新成果，是我国造纸工业理论性强、水平高的学术性期刊。它为我国造纸工业提供了一个极好的学术交流平台，对国内造纸工业的技术进步做出了较大贡献。本刊的固定栏目有：研究论文与综述等。

a3＋b3＋c3≥3abc.

在证法1中,为何a3＋b3＋c3－3abc中含有a＋b＋c这一因子,如果从行列式的角度来看,一切都显然了.

证法6 借行列式,一目了然

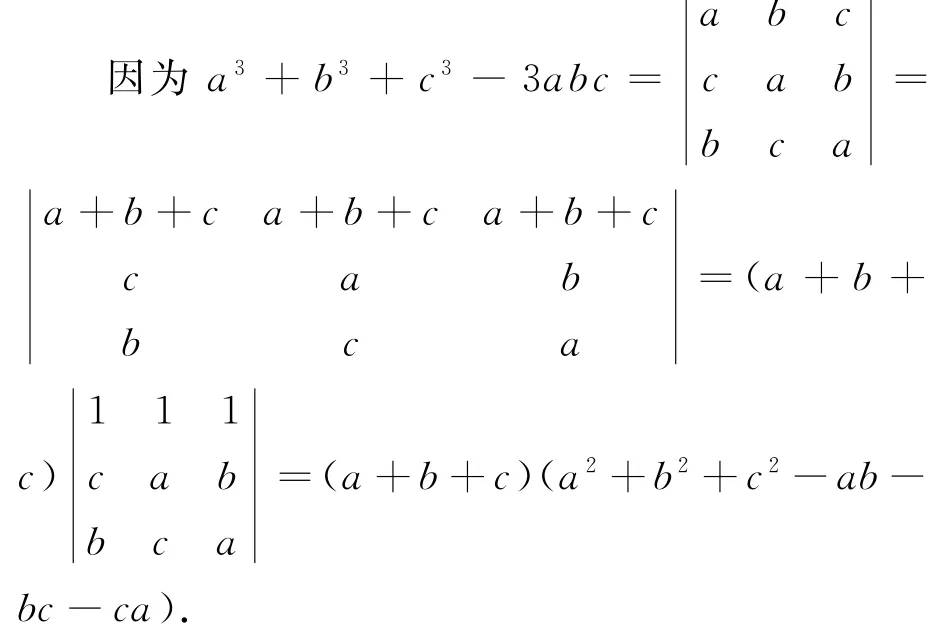
以下同证法1.

分析法是证明不等式的一种既自然又重要的方法,不等式①可否用分析法来证呢?

证法7 增量换元,柳暗花明

由对称性,不妨设a≤b≤c,令b＝a＋x, c＝a＋y,则x≥0,y≥0.

所以要证a3＋b3＋c3≥3abc,

只需证a3＋(a＋x)3＋(a＋y)3≥3a(a＋x)(a＋y),

因为x3≥0,y3≥0,a＞0,x2＋y2≥xy,所以不等式④是成立的,故不等式①成立.

不等式①是一个左、右两边都关于a、b、c对称的三元齐次不等式,由对称性,若视其中一个字母(如a)为变量,另两个字母(如b、c)视为常量,则可考虑函数f(a)＝a3＋b3＋c3－3abc,这样将不等式①的证明转化为证明函数f(a)的最小值大于或等于零.

证法8 函数搭台,导数唱戏

令函数f(a)＝a3＋b3＋c3－3abc,a∈(0,＋∞),其中b、c为常数.由于f′(a)＝3a2－3bc＝3(a＋＝0,得舍去).所以当时,f′(a)＜0;当,＋∞)时,f′(a)＞0,由函数的单调性可知,

故a3＋b3＋c3≥3abc.

证法9 构造向量,耳目一新

两边平方并整理,得

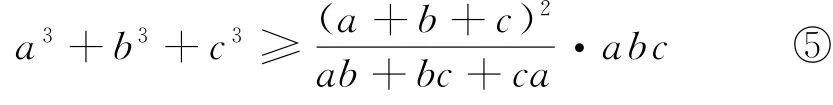
不等式③两边同加上2(ab＋bc＋ca)并整理,得(a＋b＋c)2≥3(ab＋bc＋ca)⑥

由不等式⑤、⑥即得

a3＋b3＋c3≥3abc.

证法10 排序原理,神奇优美

由对称性,不妨设a≥b≥c,

所以a2≥b2≥c2,

由顺序和大于或等于乱序和,得

a·a2＋b·b2＋c·c2≥a·b2＋b·c2＋c· a2,即

a3＋b3＋c3≥ab2＋bc2＋ca2⑦

又由a≥b≥c,得ab≥ac≥bc,

由乱序和大于或等于反序和,得

a·ac＋b·ba＋c·bc≥a·bc＋b·ac＋c· ab,即a2c＋b2a＋c2b≥3abc⑧

由不等式⑦、⑧即得

a3＋b3＋c3≥3abc.

下面证法11、12,新颖、神奇、简单,都是通过巧妙构造,并多次运用二元均值不等式给出不等式①的证明,虽然不易想到,出乎意料,但又在情理之中.

证法11 整体换元,巧妙构造

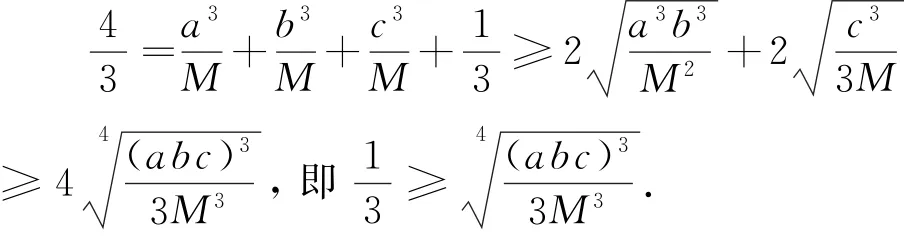
令M＝a3＋b3＋c3＞0,所以两边四次方并整理可得M3≥(3abc)3,即M≥3abc,所以a3＋b3＋c3≥3abc.

证法12 均值换元,马到成功

8A＝a3＋b3＋c3＋5A＝(a3＋A)＋(b3＋A)＋(c3＋A)＋2A≥2＋2＋2A≥4≥,即A≥≥(abc)3A5,即A3≥(abc)3,A≥abc.

故a3＋b3＋c3≥3abc.

不等式①简洁明了、结构和谐、对称优美,如何使对不等式①的证明来得自然,学生易于接受,是一个值得认真思考的问题.在数学教学过程中,应注重结论的推导(即证明),切莫囫囵吞枣,直接给出结论,然后布置大量习题,把学生赶进题海,将学生变成做题的机器;应为学生创设运用数学思想发现较自然的解法的良机,为学生提供自主探究、合作交流、观察发现、拓展智力、形成数学能力的机会,这才是数学教学的最高境界.

2017-05-16)