一道期末试题的解答与思考

山东省淄博市周村区城北中学 张 俊 (邮编:2553000)

山东省淄博市周村区教师进修学校 朱向东 (邮编:2553000)

一道期末试题的解答与思考

山东省淄博市周村区城北中学 张 俊 (邮编:2553000)

山东省淄博市周村区教师进修学校 朱向东 (邮编:2553000)

在期末考试中,有一道题目让人眼前一亮,该题构图简洁,题干叙述清晰,将几何图形融于坐标平面,学生入手较易,利于激发思考,但全部做对的学生却不多,笔者对此题进行了仔细研究,产生了些许感悟,故撰此文与同仁分享.

1 原题简析

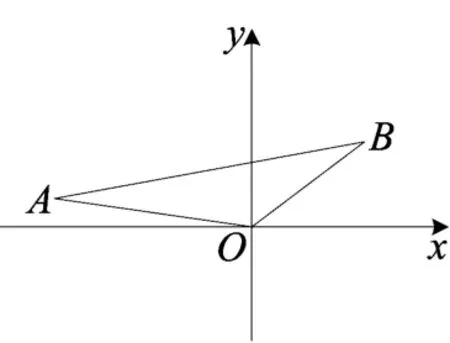
图1

题目 如图1,在平面直角坐标系xOy中,点A的坐标是(－7,1),∠AOB＝135°,OB＝5.

⑴求△AOB的面积;

⑵求点B的坐标.

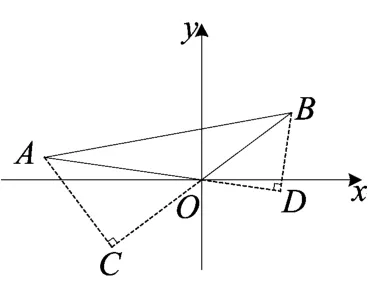
图2

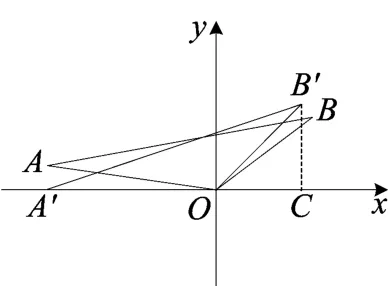
图3

分析 本题叙述文字不多,简洁、精炼.第1问难度不大,主要考查了135°角的用法,一般可以利用其邻补角45°来构建等腰直角三角形求高.如图2,可以延长BO,也可以延长AO来构造等腰直角三角形,但从计算方便的角度来看,延长BO更便捷。如果从学生更习惯于求解三角形面积时运用水平底乘竖直高的一半来计算,便可以从图形变化的角度把坐标系中的三角形AOB绕点O逆时针旋转一定角度,使OA落在x轴上得到△A′OB′,如图3,然后作B′C垂直于x轴.易得OA＝OA′＝52,在等腰直角三角形B′OC中, OB′＝5,可得,所以.然而对于第2问,多数学生感到无从下手,一些学生能直觉猜出点B的坐标为(4,3),但不能说出理由,下面笔者重点对第2问进行思路剖析.

2 解法探究

解法1 递进思考,等面积建方程

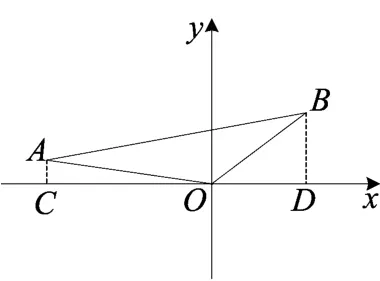
图4

利用第1问求得的三角形AOB的面积,我们依然从面积入手作为突破口,运用等面积法思考.如图4,由点A、B分别向x轴作垂线,垂足为C、D,则 S梯形ACDB＝S△AOB＋S△AOC＋S△BOD.设点B的坐标为(x,y),可得整理得x＋7y＝25①.在Rt△BOD中,由勾股定理得:x2＋y2＝25②,联合①②两个方程可求出y1＝3,y2＝4,由题意知∠BOD＜45°,所以y2＝4应舍去,即y＝3,因此点B的坐标为(4,3).

解法2 基本模型,三直角显神威

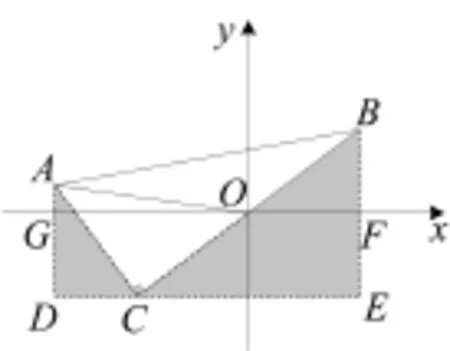
图5

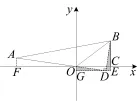
图6

由于前面已经构造了∠ACB＝90°,基于平时经验的积累,在坐标平面内我们可以构造一线三直角的模型.如图5,过点C作x轴的平行线,过点A、B分别向其作垂线,垂足为D、E,交x轴于点G、F.易得△ADC∽△CEB,因为AC＝OB＝OC＝5,所以相似比为,同时OF是△ECB的中位线,即BF＝EF＝GD＝DC.设BF＝m,在Rt△ADC中,由勾股定理得AC2＝DC2＋AD2,即25＝m2＋(m＋1)2,解得m1＝3,m2＝－4(舍去),所以点B的坐标为(4,3).

刚才我们是在∠ACB＝90°的基础上构造一线三直角(相似),同样我们也可在∠ODB＝90°基础上构造一线三直角(全等).如图6,过点D作x轴的平行线交y轴于点G,过点B作其垂线,垂足为E,过点A作x轴的垂线,垂足为F.因为△ODB为等腰直角三角形,易得△ODG≌△DBE,即OG＝DE,GD＝EB,因为∠AOF＝∠ODG,所以tan∠ODG＝1,设OG＝DE＝

7

x,GD＝EB＝7x,在Rt△DBE中,由勾股定理可得BD2＝DE2＋BE2,即225＝x2＋(7x)2,解

得x＝1.所以OC＝EG＝8x＝4,从而BC＝3,

2

点B的坐标为(4,3).

解法3 特殊一般,巧构型出相似

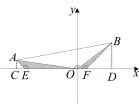
图7

解法2中的一线三直角模型是一线三等角的特殊化,我们从该模型出发,让其更具有一般性,可以构建如图7的模型.在x轴上取点E和点F,使∠AEO＝∠BFO＝∠AOB＝135°,则可借助一线三等角构得相似,即△AEO∽△OFB,相似比,再过点A、B向x轴作垂线,垂足为C、D,构建两个等腰直角形△ACE和△BDF,因为AC＝1,所以OE＝7－1＝6,因为,所以BF＝32,从而BD＝3,故点B的坐标为(4, 3).

解法4 自然生成,“8”字形找等角

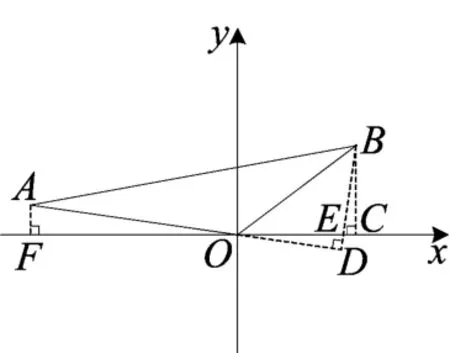
图8

由已知点A的坐标(－7,1),求点B的坐标,很自然的想到如图8,过A、B作x轴的垂线,垂足为F、C,BD交x轴于点E.结合第1问构造的等腰直角三角形BOD,在图形里面进行等角的转化.在本题中存在两个“8”字形的基本图,即△AOF与△DOE、△DOE与△BCE.易得∠AOF＝∠DOE＝∠EBC,所以tan∠AOF＝tan∠DOE＝tan∠EBC＝1.因为OD＝52,所以ED＝

7

在Rt△EBC中,设EC＝x,则BC＝7x,由BE2＝EC2＋BC2,得44590＝x2＋49x2,解得x＝3 7 (负根舍去),所以BC＝3,点B的坐标为(4,3).当然本题也可从相似的角度来看,易得△AOF∽△EOD∽△EBC,利用相似建立方程,本质同利用三角函数一样.

解法5 妙用垂直,解析法来突破

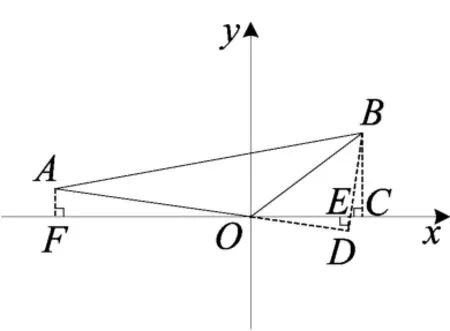
图9

本题既然以坐标系为依托,我们就可以从解析法的角度来思考.如图9,在第1问辅助线的基础上,我们由点A、点B、点D分别向x轴做垂线,垂足为点F、C、E,在Rt△OED中,很容易求出OE、ED的长度,即,此时点D的坐标为直线AD的解析式为y,因为AD⊥BD,所以直线BD的解析式可设为y＝7x＋b.把点D坐标代入,求出直线BD解析式为y＝7x－25①,设点B的坐标为(x,y),勾股定理得:x2＋y2＝25②,联合①②,最终解出点B的坐标为(4,3).

解法6 平移旋转,用变化求坐标

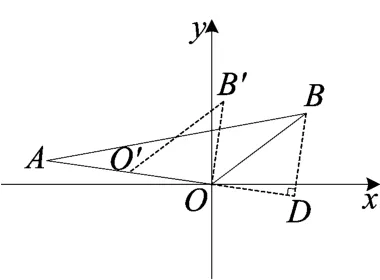
图10

图形的变换,使得几何学由静止转为动态,是学生认识图形的工具,也可以作为论证的一种手段.图形变换的学习有助于学生从运动变化的角度去认识事物,了解图形之间的联系,从而发展学生的空间观念和几何直觉.本题我们可从平移与旋转的角度思考,如图10,在第1问辅助线的基础上,我们可以把△BOD沿OA方向平移,平移的距离等于线段DO的长,得到△B′OO′,因为,所以点O′为OA的中点,其坐标为,由点O′到点B′可以看作绕点O顺时针旋转90°,易得B′的坐标为.由点B′到点B的平移和点O′到点O的平移一样,都是下移单位,右移单位,最终求出点B的坐标为(4,3).

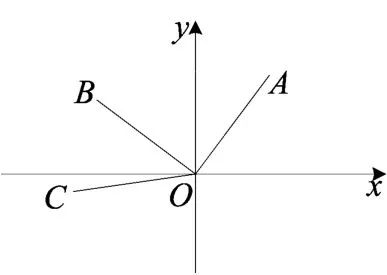
图11

本题能联系重要的数学概念和性质,解题方法多样、自然,具有发展性,我们对其适当变式:如图11,在平面直角坐标系xOy中,点A的坐标为(3, 4),将OA绕点A逆时针旋转90°得到OB,旋转135°得到OC.

⑴求点B的坐标;

⑵求点C的坐标.

简析 第1问比较基础,点B坐标为(－4, 3),限于篇幅,我们只对第2问提供两种解决思路,有兴趣的读者可以思考其它方法.

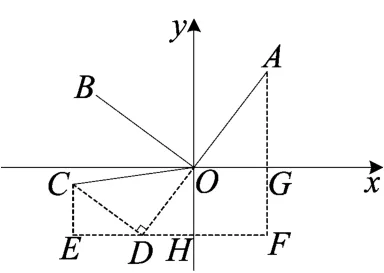
图12

方法1 几何法.如图12,基于∠AOC＝135°,延长AO构造等腰直角三角形ODC,过点D作x轴的平行线,过点A、C分别作其垂线,垂足为点F、E, AF交x轴于点G,EF交y轴于点H.从通性通法的角度,依然构造了一线三直角的模型,易得△CED≌△DHO,△CED∽△DFA,同时出现了“A”型相似图,即△AOG∽△ADF,可求出GF＝OH＝ED＝从而点C的坐标为

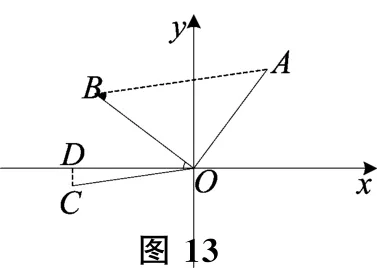
图13

方法2 解析法.如图13,连接AB,作CD⊥x轴于点D,因为△AOB为等腰直角三角形,所以∠ABO＝45°,又∠BOC＝45°,所以AB∥OC.点A坐标(3,4),点B的坐标(－4,3),易得直线AB解析式为,所以直线OC的解析式为y＝①,设点C的坐标为(x,y),在Rt△COD中,由勾股定理得x2＋y2＝ 25②,联合①②,解得:(舍去),故点C的坐标为

3 解后思考

3.1 优化解题思路,可从一题多解切入

本题解法多样,各具特色,但从学生的实际解答来看,主要为解法1和解法4,个别同学出现解法5,说明这几种方法更能贴近学生实际,一个是面积法,另一个是由相似或三角函数求角,这两种方法学生有思维经验,图形易构建,但计算量较大,对学生的运算能力是个考验.对于解法5,在坐标系中,考虑解析法是一种常规方法,但同样存在计算量偏大的问题.解法2和解法3则是典型的“多思少算”,难点在于辅助线的构建.解法2是构造一线三直角,这个模型在平时的教学中经常出现,但一般出现两个直角时学生易想,而本题只有一个直角出现,学生感到难以构造,这说明学生对一线三直角的基本模型还不能内化于心,尤其是在坐标系中出现.解法3是构造一般化的一线三等角,对学生的几何能力要求较高,离不开已有的类似经验.解法6则是一种创新解法,从坐标系中点的平移和旋转入手,给了学生以更加直观形象的思维呈现,在思路上体现出了更高的观点!平时学生习惯了静态的辅助线的作法,但对于动态地利用图形的变化来解决问题,一直是学生的薄弱点,这个方法无疑可以作为学生的能力提升来处理.

一题多解是开拓思路、培养数学能力的有效途径,应该贯穿在平时的课堂教学中.更为重要的是,它的潜在价值是在对某道题目多解的过程中,使学生看到了数学各部分知识间的联系,同时也能比较各种方法的优劣,从而在多样化中自觉地去选择最优解法.

3.2 探究问题解决,多从数形角度思考

数缺形时少直观,形缺数时难入微.本题知识内在联系丰富,集多种数学模型于一身,如“由135°想到构建等腰直角三角形”,“等面积模型”,“8”字形,“坐标平面内两条直线平行、垂直”,相似“A”型、“X”型,这些模型的掌握,既需要形的记忆,更需要数的刻画.只有数形结合,学生才会融会贯通,灵活应用.

前述题目虽有多种方法,但归纳起来无非是几何构造法和代数解析法两大类,各有特点.几何构造有时需要一定的技巧,不太好想,但计算量小;代数解析法具有一定的程序化,但有时计算较繁琐.例如解法5,抓住AD⊥BD,题目变式中利用AB∥OC,分别可以借助直线解析式中k1·k2＝－1,k1＝k2,从而找到解决问题的突破口.本题给出了现成的坐标系,很多题目图形中没有坐标系则可以合理建构坐标系来解决.对于数学题目的探究方法虽然是多角度的,但在平时的教学中教师要引导学生多从数与形两个方向来探究,即用代数的方法解决几何问题,用几何的方法解决代数问题,有时更需要两者相得益彰.

2017-06-19)