自动控制无人驾驶飞艇保持安全作业距离的数学模型研究

王国富, 刘 军, 甘德志, 林杰华, 鲍红杰, 周 立

(1.国网安徽省电力公司 安全监察质量部,安徽 合肥 230061; 2.合肥工业大学 计算机与信息学院,安徽 合肥 230009)



自动控制无人驾驶飞艇保持安全作业距离的数学模型研究

王国富1, 刘 军1, 甘德志1, 林杰华2, 鲍红杰2, 周 立2

(1.国网安徽省电力公司 安全监察质量部,安徽 合肥 230061; 2.合肥工业大学 计算机与信息学院,安徽 合肥 230009)

为了解决单纯依靠远程遥控或自控无人飞艇存在较大安全风险的问题,国家电网公司发明了带自动线控的无人飞艇应急作业方法,文章从理论上解析自动线控的数学模型。根据对牵引线受力情况分析,建立在风力、线长、高度、飞艇浮力和线控机拉力、线密度等因素作用下,飞艇与作业面保持安全距离的扩展悬链线数学模型,从而指导线控机对飞艇的实时控制。

无人飞艇；自动控制；悬链线

电力设施分布范围广,架空线路长,又处于露天运行,易受到周围环境与自然条件变化的影响，特别是在气候剧烈变化(如大风、大雪、大雾、导线结冰、暴雨等)、自然灾害(如地震、河水泛滥、山洪暴发、森林起火等)、线路过负荷和其他特殊情况时,容易发生故障,影响正常供电,给国民经济与人民生活带来很大的影响[1]。因此,通过电力应急快速到达、迅速定位并排除故障或隐患就显得尤为重要。

当有重大灾情发生,地面应急手段难以快速达到目标时,利用无人机(包括无人飞机和无人飞艇)进行低空应急将大幅提高工作效率[2],但它的控制[3]主要依靠地面指挥远程遥控和GPS引导跟踪,由于无人机易受到大风、电磁干扰、信号延迟等影响,当遥控或自控能力低于上述影响时,非常容易与带电体产生碰撞,发生危险,反而造成更大的故障。

与线路巡检[3]的要求不同,电力应急具有非计划性、区域局部性和响应的持续性,对飞行器的要求更侧重于长时间浮空和悬行、更好的稳定性和应急救援方面,这些是无人飞机技术在原理上难以突破的瓶颈。文献[4]提出利用无人飞艇对超高压输电线路进行空中巡检或应急,比无人飞机续航时间长、具有一定的抗风能力和较大的载荷量,然而其采用的依然是远程遥控和GPS定位的方式,安全性没有得到有效提高。

为此,国家电网公司发明了针对无人飞艇的自动线控安全作业方法及其装备,本文从理论上解析自动线控的数学模型，根据无人飞艇在风力、线长、高度、飞艇浮力和线控机拉力、线密度等因素作用下自动形成的自稳平衡作用,分析牵引线的受力状态方程,建立飞艇与作业面保持安全距离的扩展悬链线数学模型,从而指导线控机对飞艇的实时控制。该作业方法结合了自控、遥控和系留[5]方式的优点,使无人飞艇在低空作业时具有更高的安全性。

1 检测方法

带自动线控的无人飞艇要求在飞艇内载有高度仪、无线通讯模块、控制板、电池等,具有悬停功能和运动能力,可以实时测量与地面的距离,与地面平台无线实时通讯。本文的重点在于阐述自动线控装置控制原理。

飞艇与自动线控机之间的牵引线由于受重力作用会有一定程度的下垂,与悬链线模型类似[6],然而其不可避免受到较大风力的影响,可以看作一个特殊的悬链线。牵引线受力包括重力、飞艇的拉力、自动线控机的拉力及水平和竖直方向上的风力[7]。假定在任一时间段内,飞艇、作业面与线控机处于同一平面,则牵引线方程固定。在已知飞艇距地面高度的情况下,可以获得飞艇与自动线控机的距离,而自动线控机与作业面距离是确定的,则可以知道飞艇距离作业面的水平距离。

牵引线数学模型如图1所示。已知飞艇高度h、风力F、绳的线密度ρ、线长s、飞艇对绳向斜上方的拉力、线控机对绳向斜下方的拉力,求飞艇与作业面的水平距离M,设置飞艇的安全控制距离K和控制释放阈值R[8]。当MK+R,自动线控机随着飞艇运动自动放线。

根据受力分析,可以求得牵引线曲线方程,由于添加了风力这个额外的力,过程繁复,积分十分困难,难以直接得到曲线方程。本文从受力分析上对牵引线模型参数进行归并简化,把风力进行水平、竖直分解,竖直风力附加到重力中,相当于改变了绳的线密度,把水平风力附加到线端(飞艇端),使之作为线端力对绳的形状发生影响而不是作为一个外力对绳的形状产生影响。然后利用理想悬链线模型求出实际的曲线方程,再把改变了的参数代回,进而求出实际牵引线方程。

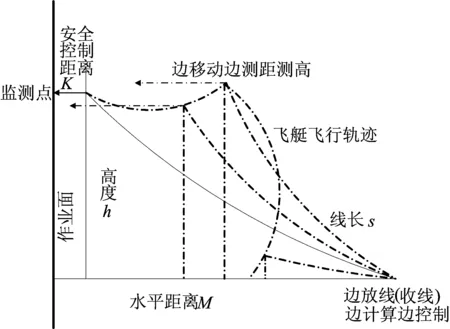
图1 牵引线收放示意图

2 模型与算法

按照自动线控要求,模型应实时解决飞艇与作业面的距离计算,提供给控制系统作为收紧或放松缆绳的依据。下面先给出理想情况下求悬链线方程的过程,将水平风力、竖直风力分别附加在线端、重力上,得到特殊的“理想悬链线方程”,再将参数回代,求得附加风力的牵引线曲线方程。

2.1 理想悬链线方程

在不考虑绳子所受风力,缆绳在完全自然下垂状态下建立的模型,是一个理想悬链线模型[9],如图2所示。

图2 理想模型受力分析

Tsinθ=mg

(1)

Tcosθ=H

(2)

(3)

mg=ρsg

(4)

(5)

又有:

(6)

则

(7)

将(7)式代入(5)式得:

(8)

可得：

(9)

则

(10)

(11)

(12)

(13)

其中,c为积分得出的常数,随坐标系沿y轴方向平移而变化。

2.2 实际模型与算法

为了便于分析,坐标和线控机位置的设置如图3所示。坐标系设置方法和图2一致,以中轴线为y轴;将线控机纵坐标置于x轴,飞艇置于曲线最顶端;虚线为理想情况下完整悬链线的延伸。

图3 实际模型受力分析

对缆绳进行受力分析,缆绳受到线控机向下拉绳的力T1、飞艇向上拉绳的力T2、绳子自身重力mg、风力在水平方向的分力Fx、风力在竖直方向的分力Fy(图中方向并不代表实际方向,只是作为分析时规定的方向),绳长s为已知量,可以通过线控机获得。其中,T1与缆绳切线的夹角为α,T2与绳子切线夹角为θ,T1、T2为可测值;mg=ρgs,因为任意时刻的绳长s与ρ均是已知的,所以缆绳的重力也是已知的;Fx、Fy可以通过风力和风向测量值计算而得。

在没有风力(Fx、Fy)情况下的曲线方程为(11)式。其中只有缆绳在最低处所受水平拉力H是变参量,绳子收紧或放松会改变H,进而改变缆绳的形状。将Fx、Fy分别叠加到T2、mg上,即将叠加后的力视作新的实际情况下的H、mg。

根据伯努利方程得到的风压方程为:

pw=0.5ρ空v2

(14)

其中,ρ空为空气密度；v为风速。风压pw与面积相乘可得Fy,即

Fy=0.5ρ空v2ds=ks

(15)

其中,d为缆绳直径。由(15)式可知,Fy与s成正比,而由(4)式,绳的重力mg也与s成正比,2个力可视为同等性质的力。将Fy附加到重力上,记做G′,成为一个特殊的重力,则可以得到(4)式的变化形式如下:

(16)

相应的线密度ρ也变成了ρ′，即

(17)

经过上述的变化后,Fy从受力分析中消失。

对于Fx,暂时先作为常数进行受力分析,则缆绳在x轴、y轴2个方向上受力平衡,平衡方程为:

T2cosθ+Fx=T1cosα

(18)

T2sinθ=T1sinα+ρ′gs

(19)

其中,Fx、T1、T2、ρ、s为已知量；α、θ为未知量。可解得T1、T2与缆绳切线的夹角α和θ为:

(20)

(21)

至此得到了实际悬链线的受力分析方程,这条悬链线必是完整悬链线(如图2)的一部分。观察理想情况下的曲线方程(11)式,该式只与完整悬链线最低点所受水平拉力H有关。而这个拉力等于悬链线顶端所受水平拉力,为了简化分析过程,把实际的牵引线延长至完整的悬链线,保持T1、T2不变,T1视作缆绳内部的拉力,T2视作端点处的拉力,将Fx附加到T2上,经此变化后,这条不完全的悬链线的受力情况与其在补齐的完整悬链线中受力完全一样,则缆绳的不完全悬链线曲线方程与完整的悬链线方程一致。在改变参量的新体系下,这是一个理想悬链线模型,可以使用理想悬链线曲线的分析方法。因此,只要求出悬链线最低点所受缆绳内部水平拉力H即可得到曲线方程。右半部分悬链线水平受力平衡,则有:

H=T2cosθ+Fx

(22)

Fx和Fy类似,与绳长s成正比,有Fx=K1s,将其代入(20)式、(21)式,则α和θ的表达式中只有s是未知量；同样地,H的表达式也只有s这个未知量。将H代入(8)式进行计算,则有:

(23)

这个微分方程过于复杂,不利于求解。分析实际应用时,s虽然是变量,但在每个时刻其值都是已知的,则H在任一时刻都是已知的,因此任一时刻的缆绳都可用悬链线方程表示,可以得到任一时刻的曲线方程,进而求得飞艇与作业面的距离,反馈给控制系统做出实时线控动作。而每次线控动作后曲线方程就会产生新的变化,因此,整个执行过程是动态的。

因此,在下面的计算过程中,α、θ、Fx视为与x、y无关的量,把(22)式带入(12)式可得如下曲线方程:

(24)

(25)

(26)

(27)

已知飞艇高度y=h,将其代入曲线方程(24)式,得到x,再减去P,可得飞艇与作业面的距离x′,同时将ρ′替换为ρ，可得:

(28)

其中,cosθ、P分别由(25)式、(26)式可知。

线控机根据计算所得的x′,将其与安全距离进行比较,结合应用要求做出收线、放线的决策。

3 结 论

基于无人飞艇在风力、浮力和拉力等因素作用下自动形成的自稳平衡作用,本文分析了牵引线的受力状态方程,建立了飞艇与作业面保持安全距离的扩展悬链线数学模型。自动线控系统依据实时计算的距离与设定的安全距离进行对比,对线控机自动发出收线、放线或保持等控制信号,从而自动控制无人飞艇与作业面保持安全距离或最佳作业距离,避免造成相撞事故。

该模型考虑了实际应用中风力的影响,比理想状态下的悬链线模型计算更准确,且由于该方法只需要在高空测量飞艇距地面高度和飞艇的拉力2个实时参数,其余参数均可在地面获得,减少了远距离传输信号延迟、误报的可能,有效避免了依赖艇载传感器提供位置数据造成的问题,有效提高了自动线控的可靠性,因此,对线控系统的设计具有一定的指导意义,实际控制效果有待实验验证。

[1] 徐静,程伟,张雷,等.无人机航测在贵州高山区电力线路工程的应用[C]//贵州省岩石力学与工程学会学术交流论文集.[S.l.:s.n.],2013:392-398.

[2] 秦宇翔,李明明,王瑞琦,等.无人机在电力系统中的应用[J].硅谷,2014(12):106,72.

[3] 林韩,林朝辉,汤明文,等.电力输电线路无人直升机巡视的应用[J].华东电力,2011,39(10):1657-1660.

[4] 廖洪涛.无人飞艇应用于超高压输电线路空中巡视可行性研究[J].技术与市场,2010,17(6):3-6.

[5] 陈有光.无人飞艇安全飞行质量保障技术与方法浅析[C]//2011年中国浮空器大会论文集.[S.l.:s.n.],2011:343-353.

[6] 郭致星,鲁束.悬链线模型与抛物线模型的差异性及其对ADSS设计的影响[J].电力系统通信,2003(11):35-37.

[7] NGUYEN T A, LEE S,PARK J S.Design and implementation of embedded hardware and software architecture in an unmanned airship [C]//Proceedings of the 2012 IEEE 14th International Conference on High Performance Computing and Communications & 2012 IEEE 9th International Conference on Embedded Software and Systems.Washington,D.C.:IEEE Computer Society,2012:1730-1735.

[8] KRISHNAMOORTHY K,PACHTER M,CHANDLER P.Maximizing the throughput of a patrolling UAV by dynamic programming [C]//IEEE International Conference on Control Applications.[S.l.:s.n.], 2011:916-920.

[9] LIU Xin, REN Wei,ZHANG Qiang,et al.Research of marine simulator cables’ mathematical models [J].Advanced Materials Research, 2014,889/890:551-554.

(责任编辑 张淑艳)

Mathematical model of automatically controlled unmanned airship for keeping safe operation distance

WANG Guofu1, LIU Jun1, GAN Dezhi1, LIN Jiehua2, BAO Hongjie2, ZHOU Li2

(1.Safety Supervision Department, State Grid Anhui Electric Power Company, Hefei 230061, China; 2.School of Computer and Information, Hefei University of Technology, Hefei 230009, China)

To avoid the safety risk caused by relying solely on the remotely or automatically controlled unmanned airship, an unmanned airship emergency operation method with automatic wire control is invented by the State Grid Corporation of China. In this paper, the mathematical model of this method is analyzed. The stress analysis is carried out on the traction line. Taking into consideration the wind force, line length, height of airship, buoyancy, pull force of wire machine, linear density and other factors, an extensive catenary model for the airship to keep safe operation distance is established. It is applied to guiding the real-time control of the airship by wire machine.

unmanned airship; automatic control; catenary

2016-03-02；

2017-05-22

国家电网公司科技资助项目(5212N013561T)

王国富(1961-),男,上海市人,国网安徽省电力公司高级工程师; 林杰华(1965-),男,安徽望江人,合肥工业大学讲师,通讯作者,E-mail:gis@hfut.edu.cn.

10.3969/j.issn.1003-5060.2017.07.008

V211.54

A

1003-5060(2017)07-0904-05