码垛机器人工作空间合理度量化评价方法及应用
2017-08-12燕培磊卢剑伟马树全
燕培磊, 卢剑伟, 马树全
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
码垛机器人工作空间合理度量化评价方法及应用
燕培磊, 卢剑伟, 马树全
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
文章提出了一种对四自由度码垛机器人工作空间合理程度进行量化评价的方法。应用D-H法建立待评价机器人坐标系,将最小长方体任务空间转化为子午面内矩形任务空间,对比分析机器人实际工作空间与矩形任务空间的偏差,并结合对于工作空间利用效率的考虑,提出了应用工作空间利用率及左侧轮廓斜率绝对值评价机器人工作空间合理程度的方法。算例验证表明,该评价方法有效,相关方法对四自由度码垛机器人的结构设计及优化有一定的指导意义。
码垛机器人;工作空间;任务空间;空间利用率;量化评价
工作空间是码垛机器人的一项重要技术指标,反映了码垛机器人的工作范围,许多学者都将工作空间作为机器人设计优化的主要优化目标之一。工作空间是否合理直接影响码垛机器人的整体性能和码垛机器人的制造成本[1-3]。
针对四自由度码垛机器人的工作空间,许多学者进行了多方面研究。文献[4]用数值方法对TH50码垛机器人的工作空间进行了求解分析,提出了机器人工作空间影响系数的概念;文献[5]分析了IRB660机器人结构参数对其工作空间的影响,并计算了相应的影响系数;文献[6]从生产线布置方面对工作空间进行了分析。上述研究都是围绕码垛机器人结构参数变化对其工作空间几何特征的影响进行分析,而没有涉及对其工作空间合理程度进行量化分析评价。
本文提出用四自由度码垛机器人实际工作空间的空间利用率及左侧轮廓线斜率绝对值对该机器人的工作空间合理程度进行量化评价,可以在设定任务空间的条件下直观、快速地判断给定的实际工作空间的合理程度,为四自由度码垛机器人的结构优化设计提供参考。
1 运动学建模及工作空间分析
1.1 结构分析
码垛机器人结构示意图如图1所示。该码垛机器人具有4个自由度及多个局部闭链,主要由腰部、大臂、小臂、腕部等组成,由下连杆、上连杆、连接三角与大臂、小臂、腕部组成2个平行四边形保证腕部机械接口始终水平,同时将小臂电机下移,与大臂电机对称放置,既增加了整个臂部的刚度,又具有行程放大功能。

1.腰身 2.大臂 3.小臂 4.腕部 5.小臂驱动臂6.小臂驱动连杆 7.下连杆 8.连接三角 9.上连杆 10.底座
1.2 运动学方程建立
针对上述码垛机器人,采用D-H参数法建立运动学模型[7]。
建立整个码垛机器人的D-H坐标系,如图2所示,0坐标系原点为底盘与腰部旋转轴线交点,5坐标系原点为腕部机械接口中心点,与之相对应的码垛机器人的结构参数见表1所列。

图2 码垛机器人机械臂机构及其杆件坐标

iαi-1ai-1diθi关节转角工作范围100d1θ1±165°2-90°a10θ2-130°~-5°30a20θ325°~155°40a30θ4从动5-90°a4d5θ5±300°
表1中,θi为连杆转角,即关节变量;αi-1为连杆扭角;ai-1为连杆i-1长度;di为沿关节i轴线2条公垂线之间的距离。
广义连杆齐次变换矩阵通式为:
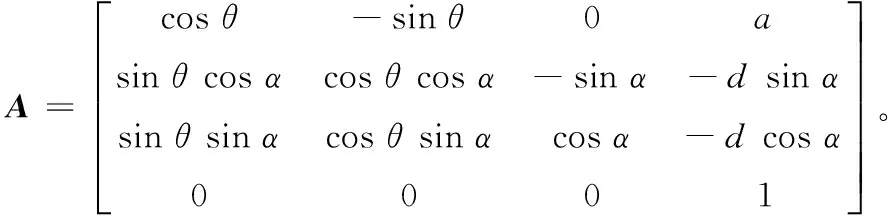
记Ai为从第i坐标系到第i-1坐标系的齐次变换矩阵,机器人底座与末端执行器之间的总变换矩阵为
(1)
将表1中数据带入(1)式,得到腕部末端位置矢量P=(px,py,pz)T,有
(2)
其中,s23=sin(θ2+θ3);c23=cos(θ2+θ3)。
1.3 工作空间分析
工作空间是机器人正常工作时腕部机械接口所连接末端执行器能达到的最大范围,它是衡量机器人性能的重要工作指标,反映了末端执行器的活动范围。
根据大臂、小臂、关节转角的工作范围以及关节干涉约束条件θ2+θ3∈(-20°,120°),得到大臂、小臂关节的工作范围示意图,如图3所示,其中由1~6线段围成的区域为大臂、小臂关节转角的实际工作范围。
根据关节转角实际工作范围的边界,结合运动方程可计算得到码垛机器人在XOZ截面上的工作空间边界,码垛机器人在XOZ截面上的工作空间是由6段弧线围成的封闭区域,如图4所示。该6段弧线中第1段线为实际工作空间的上方轮廓线,第2段线为实际工作空间的右侧轮廓线,第3段线为实际工作空间的下方轮廓线,第4段线、第5段线和第6段线按自下而上依次联接构成实际工作空间的左侧轮廓线;6段弧线的形成分别对应图3中码垛机器人关节转角实际工作范围中的第1~6条线段。

图3 码垛机器人大臂小臂关节转角实际工作范围

图4 码垛机器人工作空间在XOZ平面的投影
2 量化评价方法
2.1 矩形任务空间确定
根据给定机器人末端执行器的n个工作点可确定包容这n个工作点的最小长方体,如图5所示。该给定最小长方体的尺寸为l1×l2×l3,且在图1的D-H坐标中关于X0O0Z0平面前后对称。L为工作空间在XOZ平面投影(见图4)内第4段、第5段、第6段弧线在X轴方向的最大值。
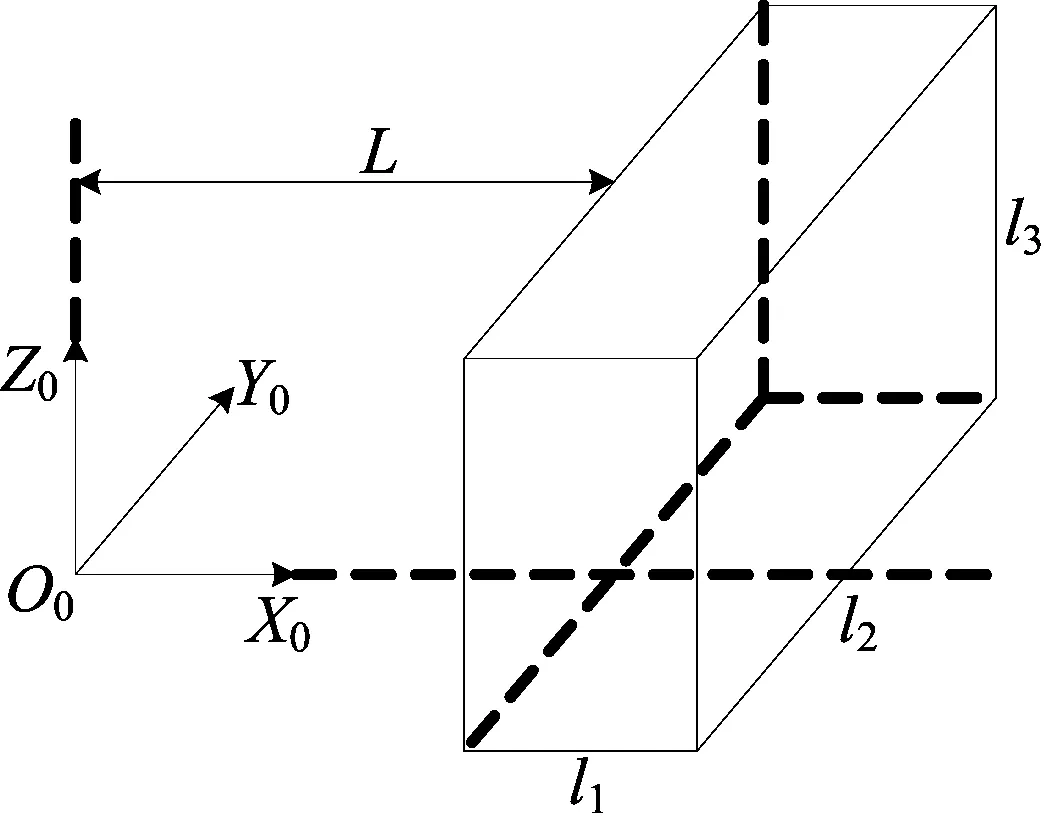
图5 给定任务空间立体图
空间内分析长方体与工作空间的位置关系过于复杂[8],本文将空间问题转化为平面问题,将最小长方体任务空间转化为子午面内矩形任务空间,大大降低了工作空间的分析评价难度。
最小长方体任务空间在X0O0Y0平面的投影如图6所示,其参数存在如下关系:
(3)
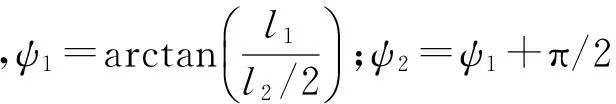
(4)

图6 给定任务空间与实际任务空间在XOY平面投影
通过(4)式可以将最小长方体任务空间转换为子午面内矩形任务空间,如图7所示。该矩形任务空间的尺寸为l×h,通过转换即可将三维空间的位置关系分析转换为在子午面内对矩形任务空间与码垛机器人工作空间的位置关系分析。子午面均可通过XOZ平面旋转得到,即可在XOZ平面进行对比分析。

图7 矩形任务空间与子午面在XOZ位置图
2.2 评价方法
根据用户提出的最小长方体任务空间转化为矩形任务空间,评价四自由度码垛机器人实际工作空间合理程度的步骤如下:
(1) 将各实际工作空间与矩形任务空间进行比较,将各实际工作空间中不能完全包含矩形任务空间的实际工作空间排除,能够完全包含矩形任务空间的实际工作空间进行步骤(2)的比较。
(2) 记矩形任务空间的面积为Sr、实际工作空间的面积为Sw,以空间利用率H作为四自由度码垛机器人的实际工作空间合理程度的第1评价指标,H越大说明四自由度码垛机器人的实际工作空间越合理。H的计算公式为:
(5)
当各实际工作空间的H相等时进行步骤(3)的比较。
(3) 记图4码垛机器人在XOZ平面投影中第4段和第6段曲线X轴方向最大值分别为maxx4、maxx6,对应点的Z轴方向数值为z4、z6,以左侧轮廓线斜率绝对值K作为四自由度码垛机器人的实际工作空间合理程度的第2评价指标,K越大说明实际工作空间的左侧轮廓线倾斜程度越小,四自由度码垛机器人的实际工作空间越合理,其中左侧轮廓线斜率绝对值为:
(6)
3 应用案例
3.1 应用案例1
用户提出一个最小长方体任务空间,转化为子午面内矩形任务空间后其尺寸为l=1 250 mm,h=1 500 mm,分别按D-H法对给定2个型号的四自由度码垛机器人建立坐标系。取这2个四自由度码垛机器人在坐标系中XOZ截面上的工作空间为实际工作空间1和实际工作空间2,如图8所示。
评价方法步骤如下:
(1) 在XOZ截面上按照平行于X轴和Z轴的方向移动矩形任务空间,如图9所示,分别将矩形任务空间4个顶点Ⅰ、Ⅱ、Ⅲ、Ⅳ的坐标值与实际工作空间1、实际工作空间2对应的轮廓线上的离散点坐标值进行比较,可知实际工作空间1和实际工作空间2可以完全包含矩形任务空间。
(2) 计算得实际工作空间1的空间利用率H=51%,实际工作空间2的空间利用率H=62%(见图9),由此可知,针对用户提出的该矩形任务空间,实际工作空间2比1的空间利用率大,判断为实际工作空间2比实际工作空间1更合理。

图8 2款码垛机器人工作空间在XOZ平面的投影

图9 2款码垛机器人工作空间利用率的对比
3.2 应用案例2
用户提出一个最小长方体任务空间,转化为子午面内矩形任务空间后其尺寸为l=1 250 mm,h=1 500 mm,分别按D-H法对给定2个型号的四自由度码垛机器人建立坐标系。取这2个四自由度码垛机器人在坐标系中XOZ截面上的工作空间为对应四自由度码垛机器人的实际工作空间3和实际工作空间4,如图10所示。

图10 2款码垛机器人工作空间在XOZ平面的投影
评价方法步骤如下:
(1) 在XOZ截面上按照平行于X轴和Z轴的方向移动矩形任务空间,如图11所示,分别将矩形任务空间4个顶点Ⅰ、Ⅱ、Ⅲ、Ⅳ的坐标值与实际工作空间3、实际工作空间4对应的轮廓线上的离散点坐标值进行比较,可知实际工作空间3和实际工作空间4可以完全包含矩形任务空间。

图11 2款码垛机器人工作空间利用率及左侧轮廓偏移率对比
(2) 计算得知实际工作空间3和实际工作空间4的空间利用率相等,均为H=51%。
(3) 计算实际工作空间3的左侧轮廓线斜率绝对值K=5.312 2,实际工作空间4的左侧轮廓线斜率绝对值K=496.712 9(见图9),由此可知,针对用户提出的该矩形任务空间,实际工作空间4比3的左侧轮廓线斜率绝对值大,判断为实际工作空间4比实际工作空间3更加合理。
4 结 论
(1) 本文将最小长方体任务空间转化为子午面内的矩形任务空间,大大简化了工作空间分析评价及机器人结构参数设计的难度。
(2) 提出了一种四自由度码垛机器人工作空间合理程度的量化评价方法,可以从空间利用率及左侧轮廓线斜率等方面对机器人工作空间合理程度进行量化评价,为机器人结构的设计及优化提供了便利。
[1] 张立杰,牛跃伟,李永泉.球面二自由度冗余驱动并联机器人可达工作空间的分析[J].中国机械工程,2009,20(24):2974-2978.
[2] GOSSELIN C M.Simulation and computer-aided kinematic design of three-degree-of-freedom spherical parallel manipulators[J].Journal of Robotic Systems,1995,12(12):857-869.
[3] 毕诸明,吴瑞珉,蔡鹤皋.工业机器人的工作空间综合[J].机器人,1994,16(3):181-184.
[4] 李金泉.码垛机器人机械结构与控制系统设计[M].北京:北京理工大学出版社,2011.
[5] 朱素霞.IRB660型码垛机器人的运动学与动力学分析[D].北京:北京邮电大学,2013.
[6] ZHANG L,MEI J,ZHAO X,et al.Layout analysis and path planning of a robot palletizing production line[C]//IEEE International Conference on Automation and Logistics.[S.l]:IEEE,2008:2420-2425.
[7] 夏链,俞晓慧,韩江,等.基于UMAC的工业机器人运动控制系统设计[J].合肥工业大学学报(自然科学版),2015,38(8):1009-1012,1090.
[8] 甘屹,王均垒,孙福佳.基于给定工作空间的6R型机器人D-H参数优化设计[J].中国机械工程,2014,25(22):3003-3007,3011.
(责任编辑 胡亚敏)
Quantitative evaluation of working space rational degree of stacking robot and its application
YAN Peilei, LU Jianwei, MA Shuquan
(School of Automobile and Traffic Engineering, Hefei University of Technology, Hefei 230009, China)
A method for quantitative evaluation of working space rational degree of 4-DOF stacking robot was presented. The smallest cuboid task space was transformed into meridian plane rectangular task space in the robot coordinate system established by D-H method. A method to evaluate the working space of the robot using the working space utilization rate and the absolute value of left profile slope was proposed through the comparison of the deviation between the actual working space of the robot and the rectangular task space. The effectiveness of the evaluation method was verified through examples. The proposed method is helpful for the structure design and optimization of 4-DOF stacking robot.
stacking robot; working space; task space; space utilization rate; quantitative evaluation
2016-01-28;修回时间:2016-02-24
教育部新世纪优秀人才支持计划资助项目(NCET-10-0358)
燕培磊(1988-),男,河北元氏人,合肥工业大学硕士生; 卢剑伟(1975-),男,山东青州人,博士,合肥工业大学教授,博士生导师,通讯作者,E-mail:jwlu75@163.com.
10.3969/j.issn.1003-5060.2017.07.004
TH122;TH242.2
A
1003-5060(2017)07-0883-05
