多目标优化下汽车车门性能分析研究

邢志波, 谭继锦, 汪小朋, 汪伟康, 潘 鹏

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.安徽江淮汽车股份有限公司,安徽 合肥 230022)



多目标优化下汽车车门性能分析研究

邢志波1, 谭继锦1, 汪小朋2, 汪伟康1, 潘 鹏1

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.安徽江淮汽车股份有限公司,安徽 合肥 230022)

文章以车门关键部件厚度为变量,采用拉丁超立方试验设计方法生成20个样本点进行计算,建立了下沉量、凹陷量、一阶模态频率、质量的Kriging模型。其中，凹陷量模型误差较大,引入抗凹刚度进行替代。为了保证合适的质量和模态频率,适当协调车门下沉量和抗凹刚度的要求,并以此为约束,以模态频率最高与质量最轻为优化目标，求得最优解。

车门;拉丁超立方;Kriging模型;刚度;模态;质量

车身轻量化技术在汽车行业发展中地位不断提高[1],而车门作为车身中的重要开闭件必须具有足够的刚度,行车时不振响、不变形,车门外板在受到人为按压时不凹陷[2],这就要求车门具有较高的下沉刚度和抗凹刚度、合适的模态频率和质量。

为了获得预测精度较高的模型,代理模型的建模方法已从传统试验设计方法和响应面法转为选用现代试验设计方法和复杂近似拟合方法[3]。

本文根据车门下沉、抗凹刚度和自由模态的分析结果,以车门关键部件厚度为设计变量,采用拉丁超立方试验设计,构建Kriging模型并使用遗传算法优化,在满足车门性能要求的条件下提高车门模态频率,质量达到最低。

1 车门有限元分析

车门由厚度不同的薄板冲压焊接形成,主要采用壳单元进行离散化[4],网格大小为5 mm,焊点采用ACM单元模拟;车门材料密度为7 850 kg/m3,弹性模量为210 GPa,泊松比为0.3。

车门有限元模型中壳单元个数为110 631个,包含110 552个四边形单元及79个三角形单元,三角形单元比例为0.08%。模型中节点个数为140 328个,焊点单元个数为145个,模型的质量为19.46 kg。

运用Optistruct求解器,分别对车门的下沉刚度(门锁处加载900 N)、抗凹刚度(刚度较小处加载100 N,模拟抗凹刚度线性段)和自由模态性能进行分析求解,在Hyperview中查看计算结果,如图1所示。

(a) 下沉变形

(b) 抗凹变形

(c) 一阶模态振型图1 车门下沉变形、抗凹变形和一阶模态振型

由图1a可知，车门垂向变形最大为5.632 mm,加载点位移为4.946 mm,小于要求变形量上限6 mm,满足要求。由图1b可知,加载点水平方向位移为1.894 mm,小于要求变形量上限2.5 mm,满足要求。图1c车门一阶模态振型图表现为车门内板的一阶弯曲,车门一阶模态频率为28.96 Hz,与模态试验结果29.54 Hz相差较小,验证了有限元模型;而车门一阶模态频率与车身的一阶弯曲模态频率(28.89 Hz)较为接近,故需对车门模态性能进行优化,与车身模态频率错开,避免行驶过程中发生共振。

2 拉丁超立方试验设计

为了构建车门各项性能的代理模型,需要进行试验设计以获取样本点。常用的试验设计方法有全因子试验、部分因子试验和拉丁超立方试验。拉丁超立方试验设计作为一种研究多因素、采样大型空间的试验设计方法,具有效率高、采样均衡性好等优点[5]。对于2因素4次试验的试验设计,全因子试验方法只能考察2个水平,拉丁超立方法则能考察4个水平,其试验点在空间的排列比全因子要均匀。

在Hyperstudy软件中,以车门内板厚度T1、外板厚度T2和内板加强版厚度T3为设计变量,其中T1和T2取值范围为0.50～1.50 mm,T3取值范围为1.00～2.00 mm;以下沉工况下加载点位移d1、抗凹工况下加载点位移d2、车门一阶模态频率f以及车门质量m为响应。应用拉丁超立方试验设计进行3因素20水平的试验设计,可得到20组样本数据。

3 Kriging模型

3.1 Kriging模型建模

Kriging方法是一种常用的构建代理模型的方法,能够利用方差的变化来表达空间的变化,而且可以保证由空间分布得到的预测值误差最小。随着计算机技术的飞速发展,该方法被运用于计算科学,产生Kriging模型,该模型作为一种代理模型可以提高计算效率[6]。

以试验设计所得的样本数据为基础,采用Kriging方法建立车门下沉量、抗凹变形量、一阶模态频率和车门质量的代理模型。其中T1和T2的车门下沉量Kriging模型如图2所示。

图2 T1和T2的车门下沉量Kriging模型

3.2 模型精度分析

代理模型的精确程度直接影响最终优化结果的可靠性[7]。因为Kriging模型精确通过样本点,所以该模型的精度分析采用检验设计空间任意样本点的相对误差和平均相对误差,其表达式[8]为:

(1)

(2)

(3)

在设计空间选取10个样本点,每个样本点的各响应相对误差和平均误差见表1所列。

表1中，d1、d2、f、m的平均误差分别为0.35%、32.48%、0.11%、0.02%,单一样本的最大相对误差分别为1.82%、162.47%、0.22%、0.10%。除d2模型误差很大超出工程要求之外,其他模型均满足工程要求，且Err,d1>Err,f>Err,m。这是由于车门质量m完全取决于车门各个部件的厚度,车门一阶模态振型为内板弯曲,f主要由车门内板厚度确定,而d1与车门部件厚度和车门结构等相关。这些参数与车门部件厚度的非线性程度较低,因此Kriging模型误差较小。

表1 样本点相对误差

d2与部件厚度非线性程度较高,但是d2的倒数与部件厚度非线性程度较低,因此本文引入抗凹加载点处的抗凹刚度k,其Kriging模型相对误差见表2所列。

表2 样本点抗凹刚度相对误差

由表2可知,k的平均相对误差为0.85%,最大相对误差为4.92%,说明k模型的精度远高于d2模型,且平均相对误差不到1%,满足工程要求,最大相对误差小于5%,基本满足工程要求。

4 优化及结果分析

4.1 优化分析

在多目标优化中,虽然有可能在可行域中存在某一点能够同时优化所有目标,但是通常的情况是目标间相互冲突[9]。 提高某些重要的响应性能可能会降低其他响应性能,使每个目标函数同时达到各自最优值的解是不存在的[10]。

为了保证车门质量处在较低的水平,错开车门与车身模态频率,必须协调车门性能要求,适当放宽车门刚度要求,因此优化要求为：① 车门下沉刚度和抗凹刚度应当满足要求,在下沉及抗凹工况下车门最大变形应分别小于6.0、2.5 mm;② 车门一阶模态频率较低会发生共振,因此车门一阶模态频率应尽量大;③ 考虑到车身轻量化的要求,车门质量越小越好。

综合以上分析,车门优化模型为:

(4)

4.2 优化结果分析

采用多目标遗传算法求解基于Kriging代理模型的多目标优化模型,所得解集如图5所示。从所得的Pareto解集中,选取合适的解为最优解,考虑到实际板材型号尺寸,对优化结果进行调整。

图5 Pareto优化解集

选定车门内、外板厚度分别为0.90、0.70mm,内板加强板厚度为1.25mm,并带入有限元模型中进行仿真分析,将其结果与Kriging模型预测值相比较,结果见表3所列。

表3 优化结果相对误差

由表3可知,d1、f、m的相对误差小于1%,k的相对误差小于3%,再次验证了Kriging模型的可信度。将最终优化结果与原车门的参数相比较,结果见表4所列。

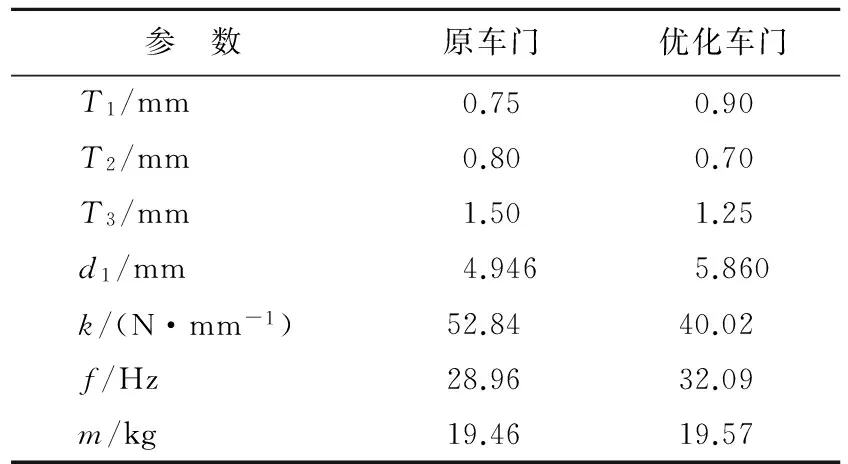
表4 优化前、后车门性能参数对比

由表4可知,在维持车门质量基本不变、刚度满足要求的情况下,优化后车门比原车门的一阶模态频率提高了3.13 Hz,并且与车身频率避开。

5 结 论

本文通过构建车门下沉量、抗凹刚度、一阶模态频率以及质量的Kriging近似模型,并用Kriging模型代替有限元模型进行快速寻优计算,协调车门性能要求,实现多目标优化。在保证车门刚度性能的前提下,提高了车门的一阶模态频率,并且使车门质量最轻,有效提高了车身静动态性能。

[1] 刘云刚.基于刚度和耐撞性的车门结构轻量化设计研究[D].广州:华南理工大学,2013.

[2] 栾文哲.某轿车车门综合性能的评价及优化设计[D].太原:中北大学,2014.

[3] 朱茂桃,钱洋,顾娅欣,等.基于Kriging模型的车门刚度和模态优化[J].汽车工程,2013,35(11):1047-1050,1042.

[4] 王国春,成艾国,胡成辉,等.基于Kriging模型的汽车前部结构的耐撞性优化[J].汽车工程,2011,33(3):208-212.

[5] 方开泰.均匀试验设计的理论、方法和应用:历史回顾[J].数理统计与管理,2004,23(3): 69-80.

[6] 邹林君.基于Kriging模型的全局优化方法研究[D].武汉:华中科技大学,2011.

[7] 徐小东,谷先广.薄壁结构抗弯性能多目标优化设计方法研究[J].合肥工业大学学报(自然科学版),2015,38(4):446-449,462.

[8] 谢延敏,于沪平,陈军,等.基于Kriging模型的可靠度计算[J].上海交通大学学报,2007,41(2):177-178.

[9] 方柘林,王丽娟,陈宗渝,等.基于车门结构的多目标优化设计方法研究[J].机械设计,2014,31(8):60-64.

[10] ZOU T,MAHADEVAN S.Multi-objective RBDO for automotive door quality design:SAE Technical Paper 2005-01-0346[R].[S.l.]:SAE,2005.

(责任编辑 胡亚敏)

Analysis of the performance of car door under multi-objective optimization

XING Zhibo1, TAN Jijin1, WANG Xiaopeng2, WANG Weikang1, PAN Peng1

(1.School of Automobile and Traffic Engineering, Hefei University of Technology, Hefei 230009, China; 2.Anhui Jianghuai Automobile Co., Ltd., Hefei 230022, China)

Taking the thickness of key parts of car door as variable, 20 sample points are produced and tested by using Latin hypercube method. The Kriging model with the sinking displacement, dent deformation, first modal frequency and mass is established. The dent resistance of the door is imported to reduce the model errors. The requirement of sinking and dent resistant performance is compromised in order to fit the mass and modal frequency. Taking this as a constraint, an optimal solution of maximum modal frequency and minimum mass is obtained.

car door; Latin hypercube; Kriging model; stiffness; modal; mass

2016-01-15；

2016-03-16

合肥工业大学产学研校企合作资助项目(W2014JSKF0445)

邢志波(1990-),男,安徽合肥人,合肥工业大学硕士生; 谭继锦(1960-),男,安徽合肥人,合肥工业大学副教授,硕士生导师,通讯作者,E-mail:tanjijin@hfut.edu.cn.

10.3969/j.issn.1003-5060.2017.07.005

U463.834

A

1003-5060(2017)07-0888-04