扩展ReliefF的两种多标签特征选择算法
2017-08-12马晶莹宣恒农
马晶莹 宣恒农
(南京财经大学信息工程学院 江苏 南京 210000)
扩展ReliefF的两种多标签特征选择算法
马晶莹 宣恒农
(南京财经大学信息工程学院 江苏 南京 210000)
针对ReliefF算法局限于单标签数据问题,提出两种多标签特征选择算法Mult-ReliefF和M-A算法。Mult-ReliefF算法重新定义了类内最近邻和类外最近邻的查找方法,并加入标签的贡献值更新特征权重公式。M-A算法在Mult-ReliefF算法的基础下,利用邻域能去除冗余的特性,更多地去除冗余特征达到更好的降维效果。采用ML-KNN分类算法进行实验。在多个数据集上测试表明,Mult-ReliefF算法能提高分类效果,M-A算法能获得最小的特征子集。
多标签分类 特征选择 数据降维 ReliefF 邻域粗糙集
0 引 言
在传统的分类任务中,每个样本仅有一个类别标签。然而在许多现实问题中,一个对象能够同时被多个标签标记,这称为多标签分类[1]。比如说一幅图片可以同时标记为“蓝天”和“大海”;一部电影同时分类为“动作片”和“喜剧片”;一位病人被诊断患有多种疾病等。多标签分类技术近年来备受关注,并且被不断应用到多个领域中如多媒体内容的自动标注[2]、生物信息[3]、Web挖掘[4]、信息检索[5]和个性化推荐[6]等。在多标签分类中,样本是由高维数据描述的,描述样本的特征数量一般较多,其中存在大量冗余和不相关的特征,这会使得后继分类工作难度增加。特征选择是指从原始特征集中,选出能使某种评价标准最优的特征子集。在分类任务前,对特征集约简,能够有效减少描述样本的特征个数,缩短运行时间,提高分类精度。
文献[7]在粗糙集理论基础上,利用邻域粗糙集的下近似和依赖度,设计适合多标签数据的特征选择算法,并验证算法的有效性。但是该算法没有考虑标签之间的相关性并且不适用高维稀疏数据。文献[8]将遗传算法和主成分分析法结合,同时应用贝叶斯分类器的方法完成特征提取。但是由于使用的主成分分析法只能用于特征值连续的数据,所以导致该方法有一定的局限性。文献[9]通过子空间降维和映射降维两种映射策略来定义一个低维特征空间,这种映射仍然采用核矩阵。文献[10]使用特征和标签之间的信息增益删除不相关的特征,达到降维的目的,但忽略了特征之间的相关性。
ReliefF[11-12]是一个经典的特征选择算法,利用特征与类别之间的相关性大小来评判特征好坏,好的特征能使同类样本靠近,异类样本远离。但是它没有考虑到标签共现的情况,所以只适用于单标签数据。本文算法扩展ReliefF算法,重新定义最近邻样本,加入标签对特征的贡献值,实现了多标签分类任务的特征选择,并通过实验验证该算法的有效性。ReliefF算法通过特征权值的排序选择前k个,不能去除冗余的特征,因此扩展的算法也有这一不足。结合文献[7]考虑到粗糙集能通过删除冗余条件属性来实现属性约简,进行二层特征约简,实验表明能更好地降低特征维度。
1 多标签的特征选择算法
1.1 单标签ReliefF特征选择算法
Kira和Rendell在1992年提出的Relief算法只适用于两类数据的特征选择,而实际应用中多类问题存在更多。随后两年,Kononenko在Kira工作的基础上提出了ReliefF算法解决了多类问题。ReliefF算法的基本思想:在训练集中选取m个随机样本,对每个样本找到它的k个类内最近邻(Hit)和类外最近邻(Miss),求出样本各特征与类别的相关性,求平均得到各特征的权重。将特征的权重排序,根据设定的阈值来选择有效特征。
记训练样本集U={(x1,y1),(x2,y2),…,(xn,yn)},其中xi∈Rn是样本的属性空间,p为样本属性个数;yi∈RL为样本类别空间,L为所给单标签数据集的类别个数。
在样本空间中:
每个样本的类别标签满足:
(1)
每一个样本只能被一个标签标记,所以ReliefF算法只适用于单标签数据。
算法1 ReliefF算法
输入:训练数据集U,迭代次数m,最近邻样本个数k
输出:特征权重向量W
(1) 初始化W(1:p)=0.0;
(2) fori=1∶m
(3) 从U中随机选择一个样本记Ri;
(4) 找到与样本Ri同类的k个最近邻Hj;
(5) for eachC≠Class(Ri)
(6) 找Ri不同类的k个最近邻Mj(C);
(7) fora=1∶p
(9) end
(10) end
(11) end
Hj表示与样本Ri同类的第j个样本,Class(Ri)表示样本Ri所包含的类别标签,d(a,x1,x2)表示样本x1和x2关于特征a的距离,P(C)表示类别C的概率,Mj(C)表示类别C的第j个样本。最终得到所有特征的权值,权值越大表示该特征对样本的区分能力越强,设定阈值选择符合条件的特征从而达到降维的目的。
在这里Class(Ri)只包含一个标签,从算法1的(4)、(6)中可以看出寻找的最近邻是以某个样本属于某一类为前提的,没有考虑样本同时拥有多个标签的情况。所以ReliefF算法只针对单标签数据,而当Class(Ri)是一个标签集合时不再适用,对于多标签数据的特征选择问题需要进一步研究。
1.2Mult-ReliefF特征选择算法
现实中大多数据并不能清晰地划分为多个不相交的类别,每一个数据样本均可能同时属于多个类别。若在多标签中能很好地找到随机样本的最近邻那么ReliefF算法也能用于多标签数据。基于此本文提出了Mult-ReliefF算法解决查找最近邻问题,并且考虑每个标签对属性的贡献值,更新权值公式。
一个样本R可以被一个或一个以上标签标记,将样本R的标签看作一个集合LR,全部样本空间看作全集L,那么样本标签的补集CLLR就被定义为样本R的不同标签集。记L(x)表示为样本x的标签集合,那么定义同类样本满足,非同类样本,相关模糊样本。
又在多标签数据中,每个样本的标签满足:
{x|L(x)∩LR≠∅∧L(x)∪LR=LR},非同类样本
{x|L(x)∩LR≠∅},相关模糊样本
{x|L(x)∩LR≠∅∧L(x)∪LR⊃LR}。
又在多标签数据中,每个样本的标签满足:
(2)
所以不考虑L(x)为空集的可能。
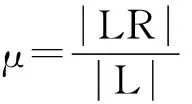
对随机选择的样本R,若查找不到k个近邻,则重新选择随机样本。根据新的类内最近邻样本和类外最近邻样本的定义,可以很好地解决ReliefF算法不能处理样本类别共现问题。在迭代更新权值时,将标签的贡献值加入到公式中,改进特征权值的更新公式更好地调节权重分配。
算法2 Mult-ReliefF特征选择算法
输入:样本的特征矩阵X,样本的标签矩阵Y,迭代次数m,近邻样本个数K
输出:特征的权值向量W
(1) 初始化W(1∶p)=0.0;
(2) fori=1∶m
(3) 从U中随机选择一个样本记Rj;
(4) 找到与样本Ri标签集合LR;
(5) for each Class(Ri)⊆LR
(6) 找Ri同类的k个最近邻Hj(Class(Ri));
(7) for eachC⊆CLLR
(8) 找Ri不同类的k个最近邻Mj(C);
(9) fora=1∶p
(11) end
(12) end
(13) end
(14) end
Class(Ri)是LR的一个非空子集,有(2|LR|-1)种情况。与算法1不同的是这里C和Class(Ri)表示一个非空集合,它们含有的元素个数可以是一个,也可以是多个,其他符号说明同算法1。如果样本Ri和同类样本关于特征a的距离不相同,则特征a就把两个同类的样本区分开了,故要减去d(a,Ri,Hj)。相反,如果样本Ri和不同类样本关于特征a的距离不相同,则特征a就把两个不同类的样本区分开了,正是我们想要的,故要加上d(a,Ri,Mj),特征权重公式中求的是均值化差异。原来的权重公式中没有考虑标签对权重的贡献值,加入标签贡献值参数μi,考虑样本Ri的标签占标签空间的比重,对多标签数据给予重视,实验证明算法的有效性。
2 二层特征约简
特征选择的目的就是在保证分类效果的前提下,获得一个较少元素的最优特征子集。我们通过Mult-ReliefF算法获得一个特征的权重向量,特征的权值越大表示该特征区分样本的能力越强。从后面实验部分可以看出在算法2中,按照比例选择靠前的特征,分类的效果会随着选取特征比例的变化而变化,并且在多个数据集上的实验表明选取前80%能较好地提高分类精度。此时获得的特征个数只是相比原来有所减少,但对于特征基数大的,选取的特征子集的个数仍然较大。比如说一个样本有1 000个特征,按照比例选取前80%依然留有800个特征,这时特征维度还是较大的。特征排序只能远离区分样本能力弱的特征,无法去除冗余的特征,这里冗余特征是指该特征所包含的分类信息已经包含于其他特征中了。根据这一不足,又提出一种二层约简M-A算法。
粗糙集理论[13]可以通过删除冗余属性来实现约简,为了更好地去除冗余特征,利用邻域区分样本的能力[7],对算法2选取的特征子集,进一步约简去冗余。
在一个多标签邻域决策系统
定义1x∈U的δ邻域为:

(3)
〈U,Δ〉是非度量空间。
定义2 集合L关于邻域关系NB的下近似为:
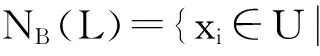
(4)
定义3 多标签分类的依赖度定义为:
(5)

定义4 条件属性a∈A-B在属性集B的基础上相对于决策属性L的重要度为:
sigγ(a,B,L)=γB∪{a}(L)-γB(L)
(6)
多标签邻域特征选择算法(ARMLNRS),基于属性的重要性来约简属性。该算法的主要思想是使用向前贪心算法依次选择具有最大重要度的特征,当sigγ(a,B,L)=0时说明特征a是多余的。
算法3 M-A
输入: 样本的特征矩阵X,样本的标签矩阵L和邻域参数δ
输出: 约简特征集feature_reduct
(1) 根据算法1得到特征权重向量W
(2) 选取排名前80%的特征,构造新的特征矩阵A
(3) 初始化feature_reduct=∅
(4) fori=1∶p
(5) 不在约简属性集的属性ai
(6) 根据式(6)计算sigγ(ai,feature_reduct,L)
(7) ifsig>0
(8) 将ai加入到集合feature_reduct
(9) end if
(10) end for
(11) return feature_reduct
二层约简算法M-A在算法2的基础下,再根据属性重要度能有效去除冗余的特征,进行二层特征筛选,实验表明能有效减少特征个数,并且分类效果相比原来的ARMLNRS有所提高。
3 实验分析
3.1 数据集
本文从Mulanlibrary下载3个多标签分类任务,如表1所示。其中,Emotions是一个关于音乐情感分类的数据集,它有593首歌,6种音乐情感,每首歌用72个特征来描述; Yeast是一个关于酵母菌基因功能分类的数据集,它包含2 417个样本,103个特征,14个标签;Scene是一个语义场景的静态索引数据集,它有2 407个实例,294个特征,6个标签。
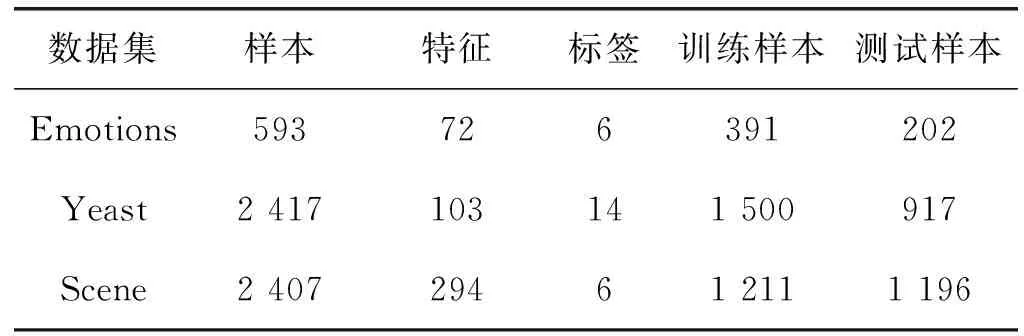
表1 数据集描述
3.2 实验设置
所有实验评估使用多标签分类模型中的算法ML-KNN[14](设定平滑参数smooth=1,邻居个数num=10),实验全部运行在3.30 GHz处理器、8.00 GB的内存空间中。
3.3 评价指标
本文根据下列5个指标[15]来评价分类效果:
(1) Hamming Loss(HL):评估预测结果与实际结果的平均差值;
(2) Ranking Loss(RL):估计有多少与样本不相关的标签的排序高于相关标签的排序;
(3) One-Error(OE):反应序列最前端的标记不属于标记集合的情况;
(4) Coverage(CV):样本标签排序的序列中,覆盖属于样本的所有标签所需搜索时间;
(5) Average Precision(AP):在样本预测排序中,排在该样本标签前的标签仍属于样本标签集的情况。
指标(1)-指标(4)越小越好,指标(5)越大越好。
3.4 实验结果
实验中,首先通过特征选择算法获得特征子集,然后对新的特征子集采用ML-KNN分类器进行多标签分类。根据文献[7]的最佳测试结果,比较在不同比例下Mult-ReliefF特征选择方法和ARMLNRS算法的平均分类精度。
由图1可以看出,对于数据样本集Yeast和Scene而言,利用Mult-ReliefF算法在80%选择后的特征子集分类效果达到最好,并且选择50%及以上的特征数目,分类效果明显高于ARMLNRS算法。而对于数据样本Emotions而言,只有在80%左右的效果比ARMLNRS算法略优。由表1可知,Yeast和Scene的标签数和描述样本的属性数比Emotions的要大,可见Mult-ReliefF特征选择算法更适合标签数和属性数较大的样本集。说明特征选择的效果和描述样本属性的个数和标记样本的标签数有关,进行数据分类时应针对数据集的特点选择合适的特征选择算法。
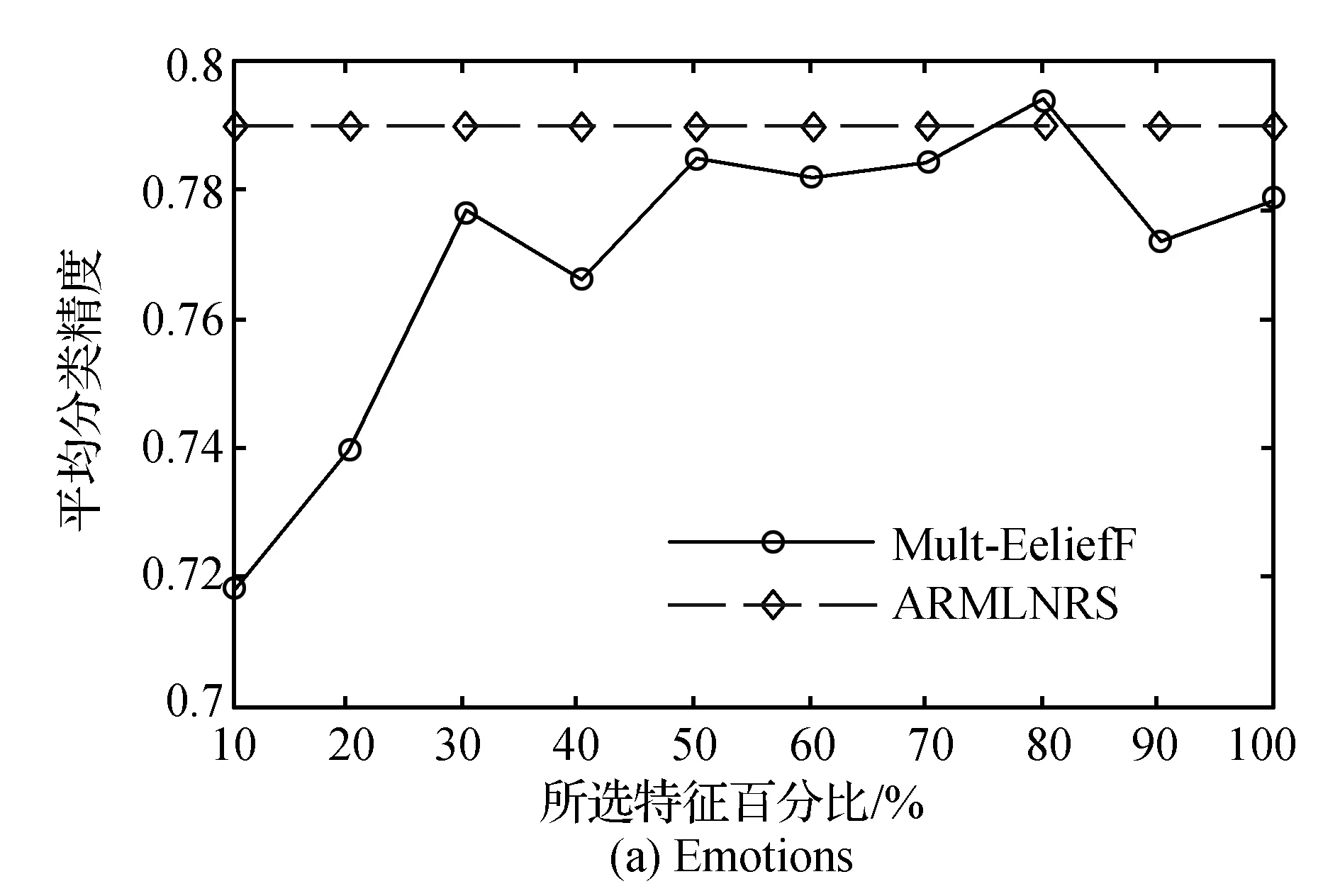
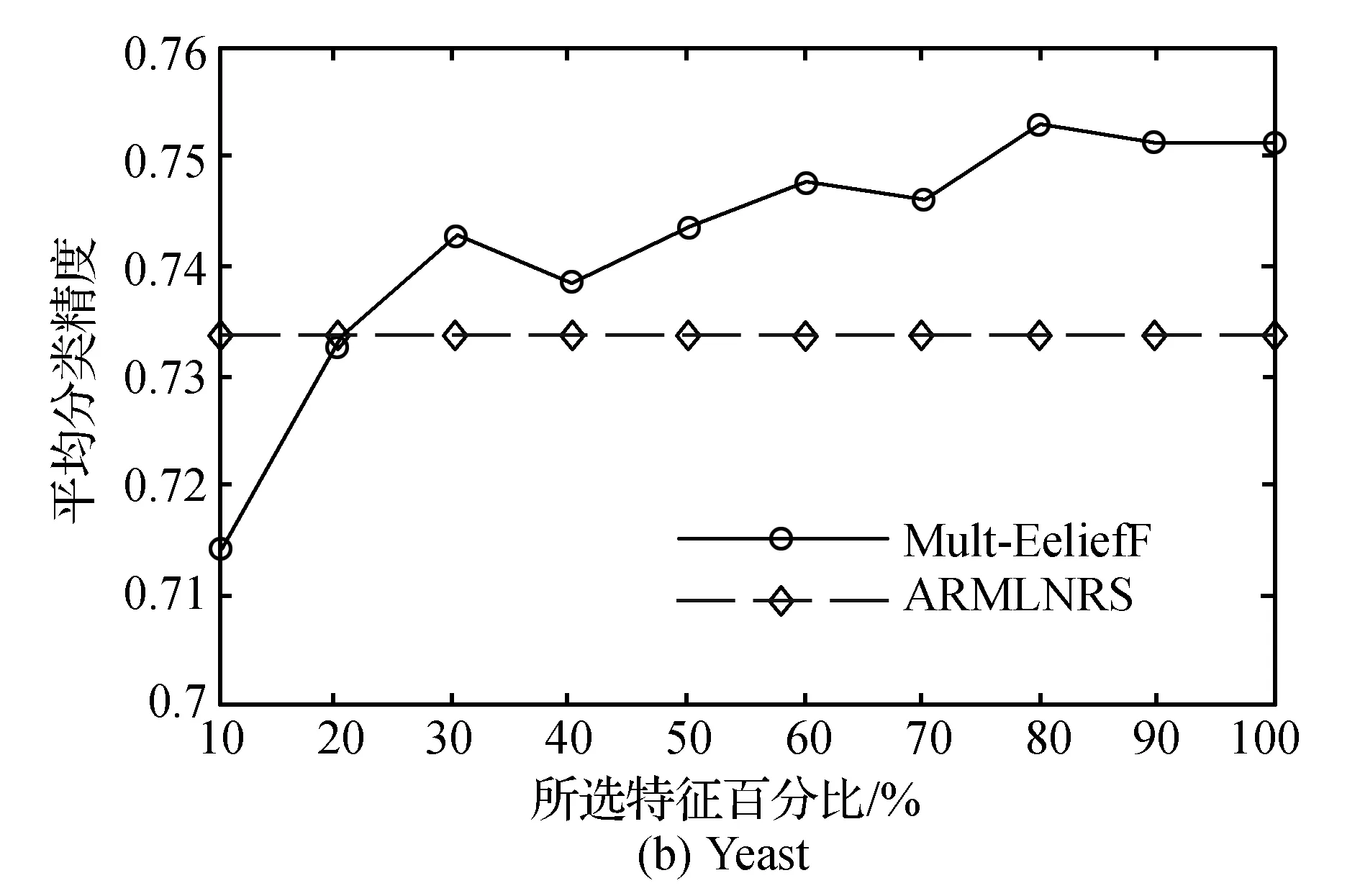
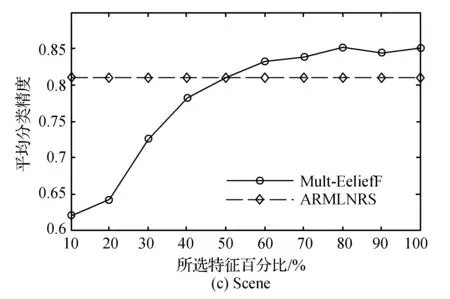
图1 三个数据集下分类精度比较
实验表明在选择样本80%左右的特征,才能获得最好的分类结果,若是样本属性个数基数大,特征排序后选择前80%后的特征数目依然不低,这样的情况下选择的是与样本关系紧密的属性,不能去除冗余。考虑到ARMLNRS算法能去除冗余特征,结合该算法做二层特征约简能在保证分类效果的前提下,尽可能获得较少的特征子集,更好地达到特征约简的目的。
实验结果如表2-表4所示。在每个数据集上比较三种特征选择方式的效果,其中,FN表示约简后的特征个数。
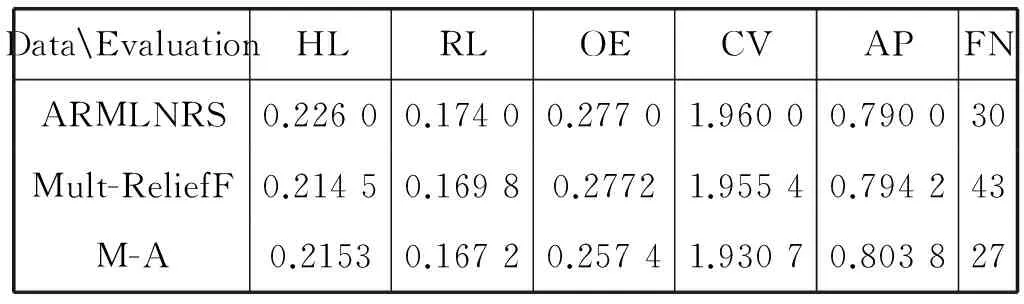
表2 Emotions下分类效果与特征子集个数对比
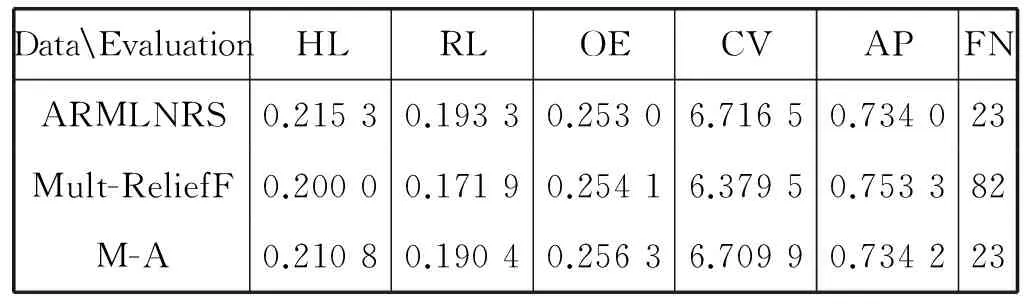
表3 Yeast下分类效果与特征子集个数对比

表4 Scene下分类效果与特征子集个数对比
从实验结果可以看出,在Emotions数据集上,M-A较Mult-ReliefF和ARMLNRS算法均有提高,而且选择的特征数目最少。在Yeast和Scene数据集下依然得到了最小的特征子集,但是分类效果不如Mult-ReliefF,却比ARMLNRS算法略优。结合两次实验,可以看出二层约简M-A算法更侧重表现ARMLNRS算法的优势,能够获得较小的特征子集,分类效果也优于ARMLNRS算法。这是由于先进行了降噪处理,然后再进行邻域下的去冗余操作,更好地发挥了ARMLNRS算法的优点,有效降低特征数目。然而,M-A算法造成了过度约简,所以效果不如Mult-ReliefF算法。Mult-ReliefF算法能有效提高分类精度,并且在数据量大的样本中表现的更为明显。总的来说,Mult-ReliefF算法在五个评价指标中都表现出优势,M-A算法能获得较小的特征子集,因此要根据需求选择合适的特征选择方法,这样更有利于提高分类的效果。
4 结 语
本文扩展了ReliefF算法,提出一种适合多标签数据的特征选择算法——Mult-ReliefF算法。该算法解决如何查找多标签样本最近邻的问题,改进了权值的更新公式,实现了数据降维的功能,实验表明该算法是有效且可行的。又由于Mult-ReliefF算法不能去除特征间的冗余性,设计了二层约简M-A算法,进一步去除冗余。实验表明M-A算法能在分类效果相差不大的情况下,获得更小的特征子集。但是M-A算法会造成过度约简,影响分类效果,接下来将研究如何避免二层约简造成的过度去噪。
[1] Zhang M L, Zhou Z H. A Review On Multi-Label Learning Algorithms[J]. IEEE Transactionson Knowledge &Data Engineering, 2014, 26(8):1819-1837.
[2] Qi G J, Hua X S, Rui Y, et al. Correlative multi-label video annotation[C]// ACM International Conference on Multimedia. ACM, 2007:17-26.
[3] Barutcuoglu Z, Schapire R E, Troyanskaya O G. Hierarchical multi-label prediction of gene function[J]. Bioinformatics, 2006, 22(7):830-836.
[4] Yang B, Sun J T, Wang T, et al. Effective multi-label active learning for text classification[C]// ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, June 28-July. 2009:917-926.
[5] Gopal S, Yang Y. Multilabel classification with meta-level features.[J]. Machine Learning, 2010, 88(1-2):315-322.
[6] Ozonat K, Young D. Towards a universal marketplace over the web: statistical multi-label classification of service provider forms with simulated annealing[C]// ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2009:1295-1304.
[7] 段洁, 胡清华, 张灵均,等. 基于邻域粗糙集的多标记分类特征选择算法[J]. 计算机研究与发展, 2015, 52(1):56-65.
[8] Zhang M L, Pena J M, Robles V. Feature selection for multi-label native Bayes classification[J]. Information Science,2009,179(19):3218-3229.
[9] Zhang Y, Zhou Z H. Multi-Label Dimensionality Reduction via Dependence Maximization[C]// AAAI Conference on Artificial Intelligence, AAAI 2008, Chicago, Illinois, Usa, July. DBLP, 2008:1503-1505.
[10] 张振海,李士宁,李志刚,等.一类基于信息熵的多标签特征选择算法[J]. 计算机研究与发展, 2013, 50(6):1177-1184.
[11] Cai Y P, Yang M, Gao Y, et al. ReliefF-based Multi-label Feature Selection[J]. International Journal of Database Theory & Application,2015(8):307-318.
[12] Spolaor N, Cherman E A, Monard M C, et al. ReliefF for Multi-label Feature Selection[C]// Brazilian Conference on Intelligent Systems. 2013:6-11.
[13] 于洪, 王国胤, 姚一豫. 决策粗糙集理论研究现状与展望[J]. 计算机学报, 2015(8):1628-1639.
[14] Zhang M L, Zhou Z H. ML-KNN: A lazy learning approach to multi-label learning[J]. Pattern Recognition, 2007, 40(7):2038-2048.
[15] Schapire R E, Singer Y. BoosTexter: A Boosting-based Systemfor Text Categorization[J]. Machine Learning, 2000,39(2-3):135-168.
TWO FEATURE SELECTION ALGORITHMS FOR MULTI-LABEL CLASSIFICATION BY EXTENDING RELIEFF
Ma Jingying Xuan Hengnong
(SchoolofInformationEngineering,NanjingUniversityofFinanceandEconomics,Nanjing210000,Jiangsu,China)
The ReliefF feature selection algorithm is limited to single-label data. Concerning this problem, two multi-label feature selection algorithms termed Mult-ReliefF and M-A are proposed. The Mult-ReliefF algorithm redefined the relationship of the nearest neighbors and updating formula of feature weights and added the label contribution to update the feature weight formula. Based on the Mult-ReliefF algorithm, combining with neighborhood rough set to achieve better effect of the feature dimension reduction, secondary reduction algorithm M-A is proposed by also adopting the ML-KNN sorting algorithm. Experimental results on data sets show that Mult-ReliefF algorithm can improve classification effect and M-A can obtain smaller feature subset.
Multi-label classification Feature selection Attribute reduction ReliefF Neighborhood rough sets
2016-09-18。马晶莹,硕士生,主研领域:数据挖掘,多标签分类。宣恒农,教授。
TP181
A
10.3969/j.issn.1000-386x.2017.07.055
