Apriori改进算法在研究影响土壤反射率因素中的应用
2017-08-12韩艳玲丰国超
孙 斌 韩艳玲 丰国超
(中国地质大学信息工程学院 湖北 武汉 430074)
Apriori改进算法在研究影响土壤反射率因素中的应用
孙 斌 韩艳玲 丰国超
(中国地质大学信息工程学院 湖北 武汉 430074)
首先简短介绍Apriori算法相关概念、改进算法的理论和实现步骤。继而通过实例试探性地将其运用到研究影响土壤反射率因素的应用中。实验结果表明:改进的Apriori算法不仅提高了产生频繁项集的效率,而且有效地减少了算法的计算时间。最后,验证并说明了关联规则、Apriori及其改进算法适用的广泛性以及有效性。
Apriori算法 土壤反射率 有机质 关联规则
0 引 言
Apriori算法[1]是由Agrawal等人提出的一种用于挖掘关联规则中频繁项集的算法[2],其最显著的特征就是应用先验知识即prior knowledge(频繁项集性质)通过迭代方法逐层搜索数据库。
Apriori 算法主要存在两方面的问题: 一是算法在每产生一次候选项集,都必须重新扫描一遍事务数据库D。对数据库规模大的情况,扫描数据库的过程将会在外部存储介质和内存之间频繁交换数据。二是连接操作和处理候选项目集的测试过程花费大量的时间。这些都将使处理的时间复杂度很大[3]。Apriori的改进算法,也都是基于这两方面考虑的[4]:减少扫描事务数据库D的次数以及删除多余的无用的候选项目集。
1 Apriori算法及其改进思想
1.1 算法简介
在关联规则中,支持度大于或等于最小支持度的项集称为频繁项集,简称频集。为了生成所有频繁项集,使用了递归的方法:先找到频繁1-项集集合L1,然后用L1找到频繁2-项集集合L2,接着用L2找L3,直到找不到频繁K项集为止,找每个Lk都需要对数据库扫描一次。然后通过得到的频集来产生关联规则,这些规则同样必须满足不小于最小支持度和最小可信度的条件,满足该条件的关联规则就是强关联规则。最后用所得的频集来产生我们所感兴趣的关联规则。
1.2 Apriori算法性质及改进
频繁项集的性质[5-6]。
性质1 频繁项集的所有非空子集也必须是频繁的。即A∪B模式不可能比A更频繁的出现。
性质2 非频繁项集的超集一定不是频繁项集。即Apriori算法是反单调的,一个集合如果不能通过测试,则该集合的所有超集也不能通过相同的测试。
Apriori算法运用第一个性质,利用已得到的或者已知的频繁项集来构造长度更大的项集,这些更长的项集成为潜在频繁项集(候选项集)。潜在频繁K项集的集合Ck指的是那些有可能成为频繁K项集的项集所组成的集合。以后只需计算潜在频繁项集的支持度,而不必计算所有不同项集的支持度,因此在一定程度上减少了计算量。
性质3 若Xk是数据集F的频繁K项目集,那么Xk中任意项的任意元素在F的降幂子集——频繁k-1项集L(k-1)的所有k-1子集合中出现次数至少是k-1次。
利用整理出来的性质3[7],我们可以对候选项集做进一步的剪枝以获得更有价值的项目集。
2 Apriori改进算法的实现
2.1 Apriori改进算法详细步骤
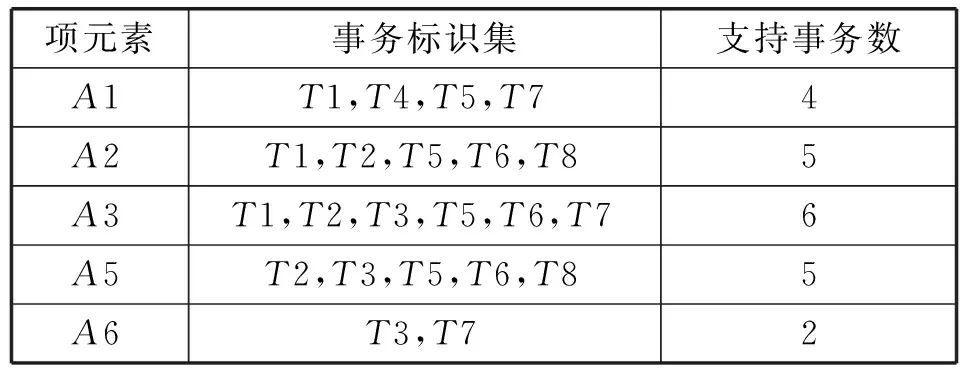
1) 扫描事务数据库产生候选项目集C1,记录每个项元素的支持事务(项目编号TID)并统计支持事务数,记录最小支持度阈值及项集。
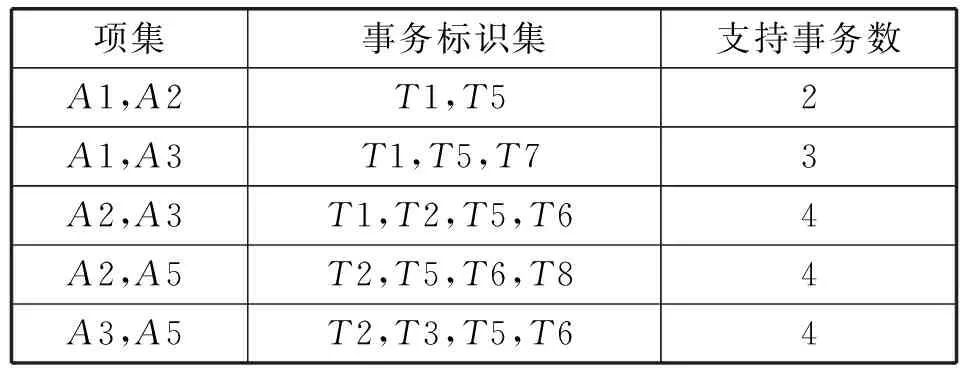
2) 把小于最小支持度阈值的项目集删除,得到L1。对L1中的项集自连接产生候选2项集C2,并对L1的项目编号做交集运算得到C2项集的事务标识集和支持事务数,删除事务数小于最小事务数的项集得到L2。
3) 用L(k-1)通过自连接生成候选K项集Ck的事务标志集(改变原算法L(k-1)进行自连接的判断方式),并对其计数。
4) 删除Ck中事务数小于最小事务数的项集,然后根据剪枝理论对频繁K项集中的项进行进一步删除,得到进一步压缩的有价值新频繁K项集。
下面给出已有剪枝方法的伪代码:
Procedure Prunel(L(k-1))
//m是L(k-1)所有项元素的个数
For all itemset li∈L(k-1)
If count(li)<=k-1
Then delete all Lj from L(k-1)( li∈Lj)
End
Return L(k-1) //返回删除L(k-1)中出现次数小于k-1的项目的项目集
对已有剪枝方法我们做些进一步改进:
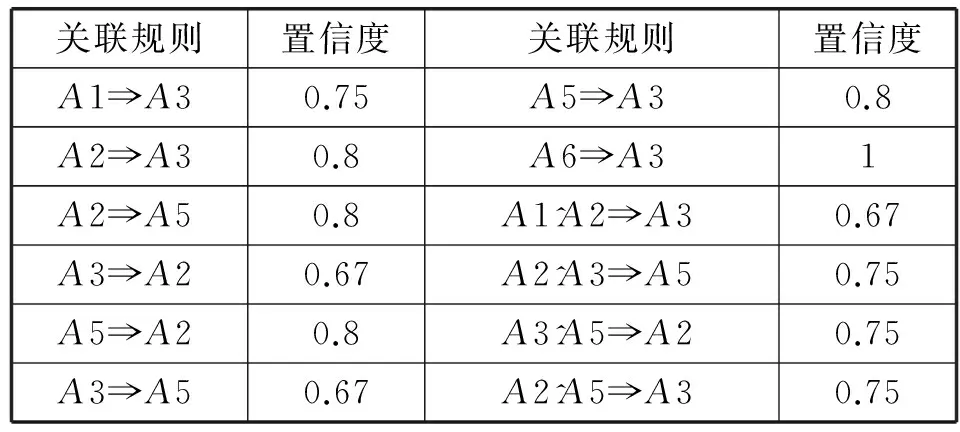
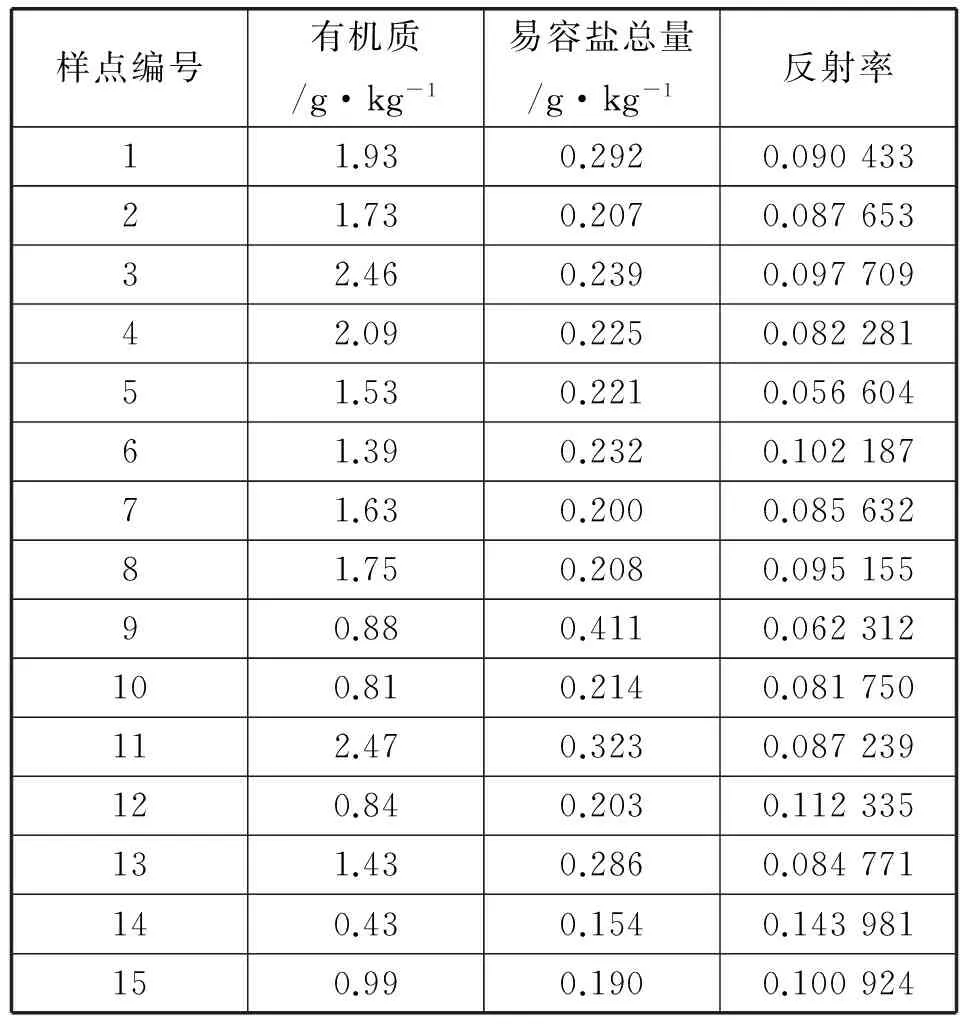
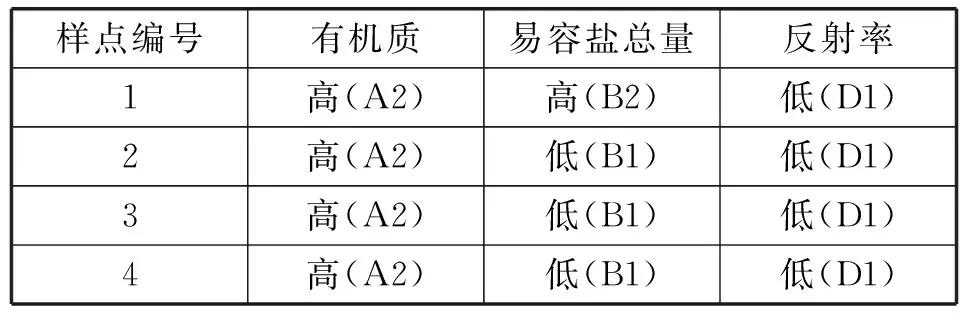
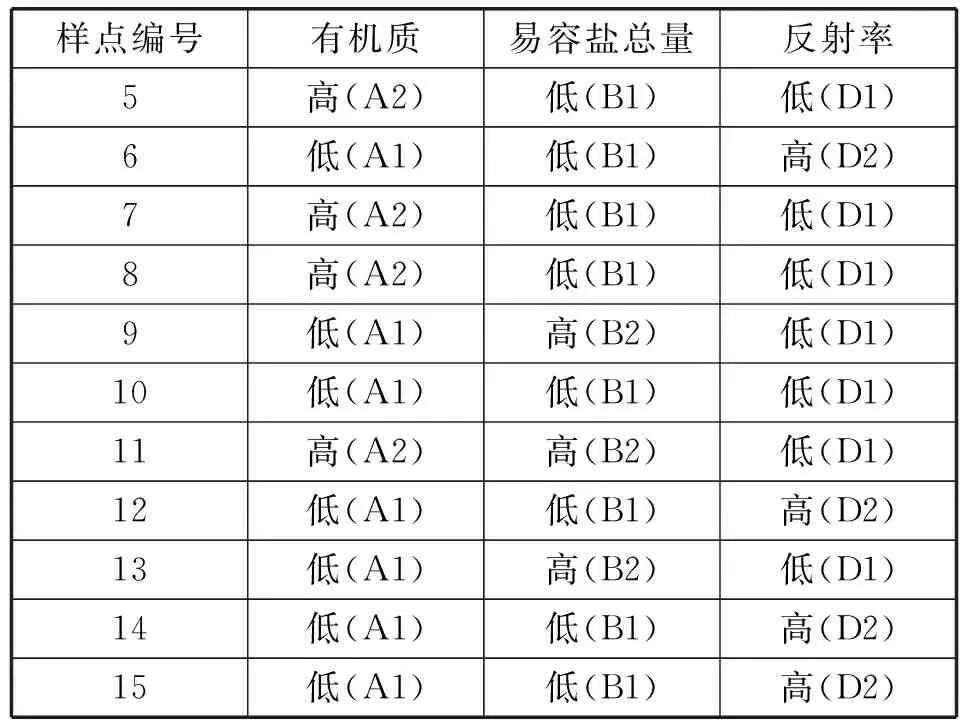
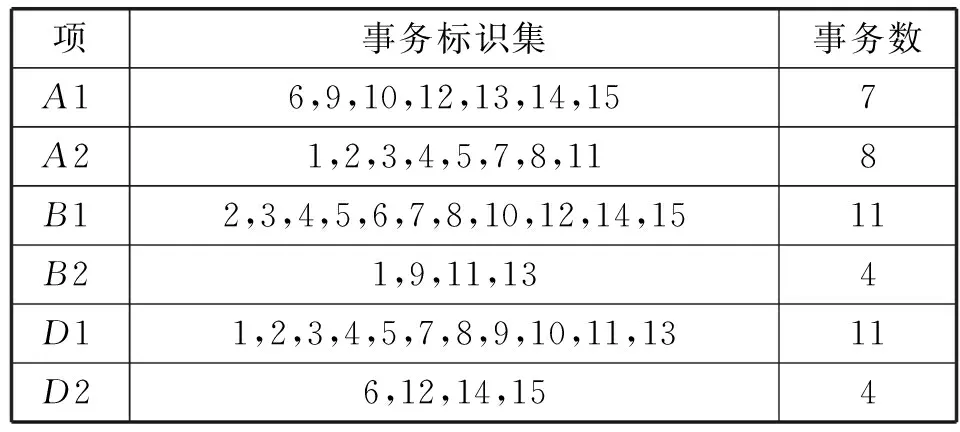
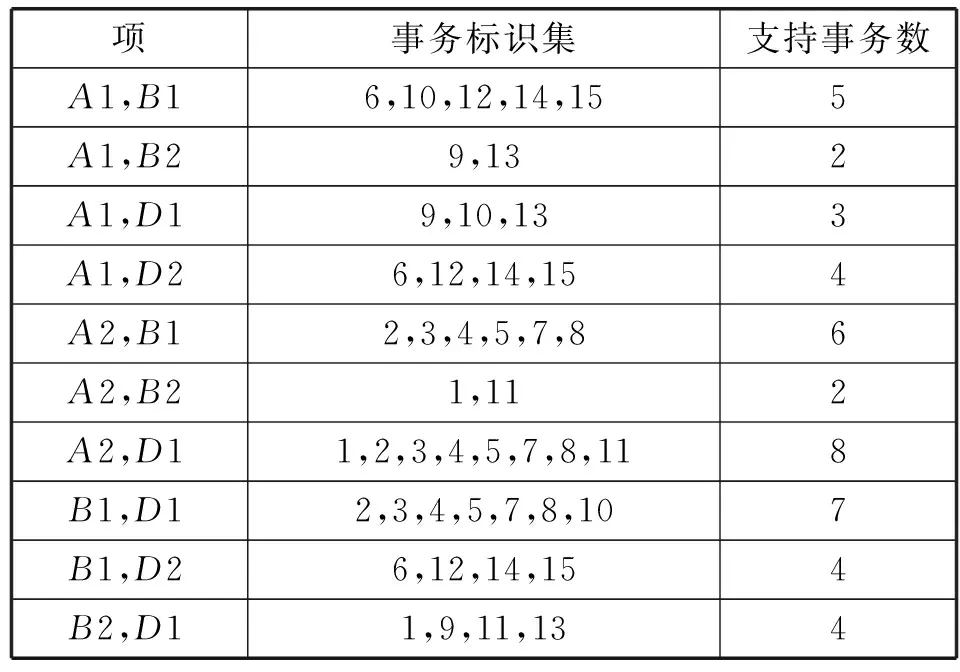
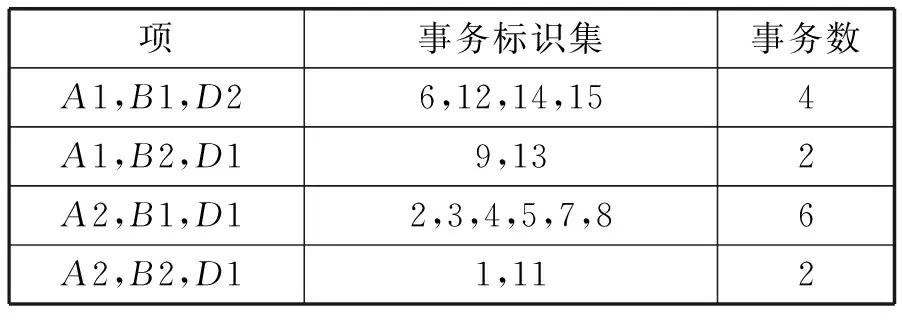
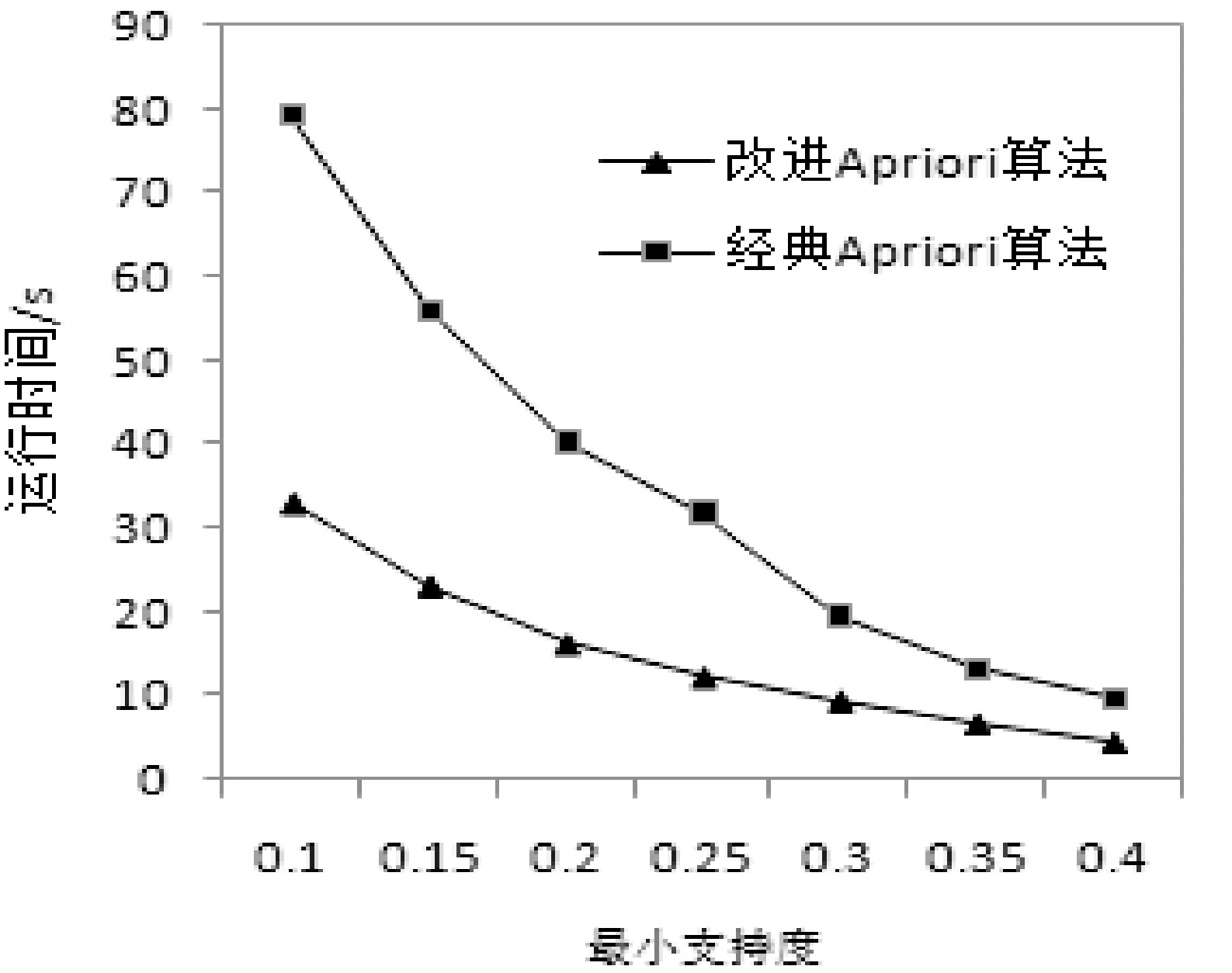
Procedure Prunel(L(k-1))
For( i=0;i For all itemset li∈L(k-1) If count(li)<=k-1 Then delete all Lj from L(k-1)( li∈Lj) m=GetNewM(L(k-1)) End End Return L(k-1) 2.2 步骤演示 假设有如下所示原始事务数据库(如表1所示),设置最小支持事务为2。 表1 事务数据库 首先对事务数据库进行一次扫描,得到数据库的全部项元素I={A1,A2,A3,A4,A5,A6}以及单个元素项的支持事务集(事务标识集)。将其中支持事务数小于2的项删除(这里删除A4),得到新频繁1-项集如表2所示。 表2 频繁1-项集 频繁1-项集自连接得到候选2-项集,再通过支持事务做交集运算得到候选2-项集和相应的支持事务集;删除支持事务数小于2的项集,得到频繁2-项集L2如表3所示。 表3 频繁2-项集L2 根据改进算法的剪枝方法对频繁2-项集L2中的项进行剪枝处理,将其中有项元素出现次数小于2的项删除。A6的出现次数小于2,所以删除包含A6的项集{A3,A6},得到新的频繁2-项集为如表4所示。 表4 新频繁2-项集 运用与生成新频繁2-项集相同的方法,生成新频繁3-项集:自连接,对支持事务做交集,删除事务数小于2的项集。得到如表5所示频繁3-项集L3。 表5 频繁3-项集L3 根据剪枝理论对频繁3-项集L3中的项进行剪枝处理,将其中有项元素出现次数小于3的项删除。由于A1、A2、A3、A5这四个项的出现次数都小于3,所以把所有项集都删除,到这一步结束,搜索出全部频繁集。 设置信度阈值为0.65,即minconf=0.65,那么产生的所有关联规则如表6所示。我们可从中选出感兴趣的规则。 表6 关联规则表 3.1 数据基础 我们知道,土壤粒度、含水量、有机质、氧化铁以及盐组分及含量都会影响土壤光谱反射率。这些因素不同的土壤,其反射率一般都会发生变化,但土壤的光谱曲线常常能保持波形不变。故这里我们可以使用关联分析对这里的某些因素进行定性分析,对这些因素在某一波段内对土壤反射率的影响进行验证。 氧化铁对光谱曲线有较大影响,我们可选对有机质较为敏感但氧化铁影响较弱的紫外波段(372.01~400 nm)和可见光波段(590~700 nm)附近[8]。而土壤有机质光谱敏感波段主要在600~800 nm,土壤有机质光谱响应范围(600~800 nm)恰是土壤光谱与水分相关系数最低的波段区域。因此我们选择这些波段的公共区域可见光波段的695 nm反射率进行分析[9]。 所得的实验数据是使用美国生产的仪器ASD FieldSpec 3在武汉市江夏区纸坊大街沿线所测。仪器采样波长范围是350~2 500 nm。在350~1 000 nm间采样间隔为1.4 nm,1 000~2 500 nm采样间隔为2 nm;在350~1 000 nm之间光谱分辨率为3 nm,1 000~2 500光谱分辨率为10 nm。测试土壤光谱时探头垂直于图样表面,光源照射方向与垂直方向夹角小于15°,探头到土壤表面距离15 cm;土壤取样深度均为20 cm,天气晴朗,风速较小,取样时间为10:30-15:00,其他因素出于实验着想,尽可能保持一致。表7为部分原始数据。 表7 原始实验数据 3.2 关联分析 我们进行关联分析的目的是为了找出影响反射率较大的属性(这里指有机质、易容盐量),并对影响趋势做定性分析。对属性数据,按一定方式离散化(有机质:1.5 g/kg 易溶盐:0.25 g/kg 反射率:0.1)。如表8所示。 表8 离散化的属性表 续表8 对离散化后的数据进行关联规则挖掘,设最小支持度为10%,最小置信度为60%。那么整个项集所有元素为{A1,A2,B1,B2,D1,D2},根据最小支持度,最小支持事务数应该为:10%×15=1.5。如表9所示。 表9 候选1-项集 要求项的支持事务数大于或等于1.5,可以得到L1:{{A1},{A2},{B1},{B2},{C1},{C2},{D1},{D2}}。对L1进行自连接后得到候选2-项集C2,进一步对C2进行处理:删除项集中支持事务数小于1.5的项,并删除其中每个项元素出现次数小于2的所有项集,得到新频繁2-项集L2。表10就是满足条件的新频繁2-项集L2。 表10 新频繁2-项集L2 由L2得到候选3-项集C3,并删除支持事务数小于1.5的项后得到频繁3-项集L3,如表11所示。 表11 频繁3-项集L3 算法到此结束。最终算法挖掘出来的最大频繁模式为{A1,B1,D2}、{A1,B2,D1}、{A2,B1,D1}、{A2,B2,D1}。 3.3 结果分析 通过分析出来的最大频繁模式,计算与反射率有关规则的置信度: A1^B1⟹D2 confidence=P(D2/A∪B1)=P(A1∪B1∪D2)/ P(A1∪B1)=4/5≈80% A1^B2⟹D1 confidence=P(D1/A∪B2)=P(A1∪B2∪D1)/ P(A1∪B2)=2/2≈100% A2^B1⟹D1 confidence=P(D1/A∪B1)=P(A2∪B1∪D1)/ P(A2∪B1)=6/6≈100% A2^B2⟹D1 confidence=P(D1/A∪B2)=P(A2∪B2∪D1)/ P(A2∪B2)=2/2≈100% 选出置信度大于60%的规则: 规则一:A1^B1⟹D2 规则二:A1^B2⟹D1 规则三:A2^B1⟹D1 规则四:A2^B2⟹D1 1) 从规则一和规则三可得,随着有机质含量的增加,土壤反射率会降低。 2) 由规则一和规则二可得,土壤反射率随着含盐量增加而降低,但是由规则三、规则四则得出不一致的结论,且这些规则的置信度都很高。分析原因,土壤中易溶盐不同的组分的含量也可能是影像土壤反射率的另一因素;此外,也有可能是对数据进行处理时的最小支持度设置过低,可以进行适当调整。 3.4 算法实验与分析 为了验证改进后算法的效率,选取了影响土壤光谱反射率的全部采样数据作为样本,该数据库共有7 837条记录,在相同的硬件配置条件,不同的最小支持度下,得到改进算法与经典Apriori算法的运行时间如图1所示。 图1 算法计算时间与最小支持度的关系 从图1中可以看出,在相同记录数下,改进Apriori算法比经典 Apriori算法的运行效率有显著的提高,并且计算时间随最小支持度的增加而减小,且在最小支持度很小时,效果更为明显。 从算法本身的角度来说,改进的关联规则算法与Apriori算法比较主要有两大优势。① 缩减了扫描数据库消耗的系统I/O开销。② 候选项集的裁剪使得在剪枝和连接上时间效率得到一定程度的提高。 从实例分析角度来说,Apriori算法(及其改进理论)不仅适用于市场营销领域,在遥感数据分析方面(土壤光谱相关性分析、山火预警以及区域成矿预测[10]等)也有较好的实用性,是一种对数据、结论进行分析、验证的有力手段。但不足之处在于在进行大数据量数据分析,本文未得到验证;在进行属性数据离散化时,虽然不会导致结果的错误,但也存在部分偶然性。 [1] Agrawal R,Srikan R.Fast algorithms for mining association rules in large databases[C]//Proceedings of the Twentieth International Conference on Very Large Databases,Santiago,Chile.1994,9:487-499. [2] Agrawal R,Imielinshi T,Swami A.Mining association rules between sets of items in large database[C]//Proceedings of ACM SIGMOD Conference on the Management of Data.Washington DC.1993:207-216. [3] Ng R T,Lakshmanan L V S,Han J,et al.Exploratory mining and pruning optimizations of constrained associations rules[C]//SIGMOD 1998,Proceedings ACM SIGMOD International Conference on Management of Data,June 2-4,1998,Seattle,Washington,Usa.DBLP,1998:13-24. [4] 吴兰岸,刘延申,刘怡,等.欧美国家知识发现与数据挖掘过程模型研究及其教育领域应用启示[J].远程教育杂志,2016,35(3):24-31. [5] Han Jiawei,Kamber M.Data Mining:Concepts and Techniques[M].北京:机械工业出版社,2001. [6] Witten I H,Frank E.Data Mining:Practical Machine Learning Tools and Techniques[M].北京:机械工业出版社,2006. [7] 刘宏强.Apriori关联规则挖掘算法分析与改进[J].中国石油大学胜利学院学报,2009,23(1):17-19. [8] 杨扬,高小红,贾伟,等.三江源区不同土壤类型有机质含量高光谱反演[J].遥感技术与应用,2015,30(1):186-198. [9] 彭杰,周清,张杨珠,等.有机质对土壤光谱特性的影响研究[J].土壤学报,2013,50(3):517-524. [10] 何彬彬,崔莹,陈翠华,等.基于地质空间数据挖掘的区域成矿预测方法[J].地球科学进展,2011,26(6):615-623. APPLICATION OF IMPROVED APRIORI ALGORITHM IN STUDYING FACTORS OF SOIL REFLECTIVITY Sun Bin Han Yanling Feng Guochao (CollegeofInformationEngineering,ChinaUniversityofGeosciences,Wuhan430074,Hubei,China) Firstly, the concepts of Apriori algorithm are briefly introduced, and the theory and implementation steps of the algorithm are improved. Then, it is applied to the study of factors affecting the soil reflectivity through the example tentatively. The experimental results show that the improved Apriori algorithm not only improves the efficiency of generating frequent itemsets, but also effectively reduces the computation time of the algorithm. In the end, the generalization and validity of association rule, Apriori and its improved algorithm are proved. Apriori algorithm Soil reflectivity Organic matter Association rules 2016-06-03。孙斌,副教授,主研领域:空间数据库,GIS应用。韩艳玲,硕士生。丰国超,硕士。 TP311.13 A 10.3969/j.issn.1000-386x.2017.07.054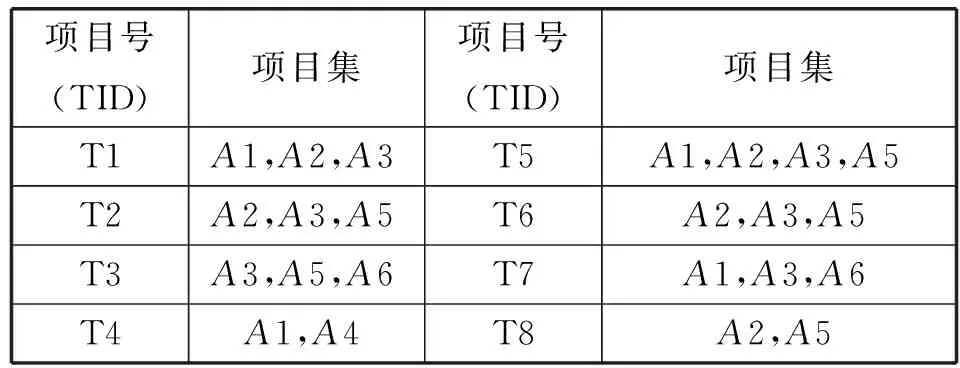


3 Apriori改进算法的应用
4 结 语
