拦截大机动目标的三维制导控制一体化设计
2017-08-11王卫红熊少锋
赖 超,王卫红,熊少锋
(1. 北京航空航天大学自动化科学与电气工程学院,北京 100191;2. 中国航天科工二院总体设计部,北京 100854)
拦截大机动目标的三维制导控制一体化设计
赖 超1,王卫红1,熊少锋2
(1. 北京航空航天大学自动化科学与电气工程学院,北京 100191;2. 中国航天科工二院总体设计部,北京 100854)
针对大机动目标拦截过程中目标加速度未知的问题,提出一种结合有限时间收敛扩张状态观测器与自适应动态面控制的复合三维制导控制一体化设计方法。首先,建立基于弹目视线坐标系下的三维全耦合六自由度侧滑转弯导弹的制导控制一体化模型,减少了假设条件;采用动态面方法,避免传统反步法设计中的“计算膨胀”问题,引入有限时间收敛的扩张状态观测器来在线估计并补偿包括目标加速度在内的不确定性,同时结合自适应鲁棒控制策略,对新型扩张状态观测器的观测误差进行补偿,有效地提高了对大机动目标的拦截精度。基于李雅普诺夫稳定性理论证明了闭环系统的稳定性。导弹六自由度全状态模型的拦截仿真证明了设计方案的有效性。
制导控制一体化(IGC);不确定性;动态面;自适应控制;扩张状态观测器
0 引 言
随着导弹技术的发展,拦截强机动目标技术是现代导弹防御系统研究的热点。传统的双回路设计是基于频谱分离的假设,分别设计制导系统与控制系统,具有优良的控制性能。但传统的双回路设计在拦截大机动目标时,导弹制导回路的时间常数比较小,带宽随之变大,此时频谱分离的假设不再成立,往往会导致导弹的末制导段脱靶量较大、弹体失稳,其性能不能满足应用需要[1]。为了解决这个问题,制导控制一体化设计(Integrated guidance and control, IGC)第一次被提出来[2]。IGC将制导回路和控制回路视为一个整体,充分利用制导与控制系统之间的耦合作用,根据导弹的运动状态与相对运动信息直接产生舵面偏转指令,最大可能地减少了面向大机动目标拦截时传统设计方法引入的时间滞后,在大机动目标拦截上有很好的潜力。
很多不同的控制方法被用来进行二维制导控制一体化设计,如小增益理论[3],自抗扰技术[4],终端滑模控制[5]等。文献[6]结合了动态面反步设计与非线性干扰观测器技术,提出了一种导弹纵向通道的IGC设计方法。文献[7]面向高速机动目标的拦截,设计了一种自适应最优滑模IGC算法。很多文献的IGC设计是以二维IGC模型作为对象进行研究,针对三维IGC模型进行设计研究虽然不多,但也有了进展。文献[8]建立了三维IGC模型,但假设初始时刻导弹速度矢量和弹目视线近似重合。θ-D方法被用来设计六自由度导弹模型的IGC设计[9]。文献[10]设计了基于反演滑模和扩张状态观测器的复合IGC方案。文献[11]重新定义了零能脱靶量,运用超扭曲二阶滑模控制理论,提出了一种IGC设计方法。在文献[12]中,针对倾斜转弯导弹,建立了三维IGC设计模型,并针对饱和、容错等设计了复合控制方法。
在拦截大机动目标时,目标加速度很难直接得到。各种不同的状态观测器用来估计并补偿目标的加速度,滑模观测器[13],扩张状态观测器[14-15],非光滑扩张状态观测器[16]等。自适应技术也应用于处理IGC系统的不确定性。文献[17]采用自适应模糊技术对系统中的不确定性进行估计,并设计了纵向平面IGC方法。文献[18]针对机动目标,使用基于Nussbaum增益的滑模自适应控制方法来设计IGC方案。在IGC设计中,很多研究是基于纵向平面或者是三通道解耦模型进行设计,对目标加速度信息进行预估与补偿。拦截大机动目标,能有效估计并补偿目标加速度不确定性的三维IGC设计研究较少。
本文考虑“地对空”侧滑转弯(Slide-to-turn,STT)导弹迎头拦截大机动目标的情形,建立了面向大机动目标拦截的STT导弹的六自由度三维制导控制一体化设计模型,不需要假设初始时刻导弹速度矢量和弹目视线近似重合。针对制导控制一体化设计中的不确定性与目标加速度信息未知的特点,采用文献[19]中的有限时间收敛的扩张状态观测器来估计IGC系统的不确定性,设计自适应控制律,对扩张状态观测器的观测误差进行补偿,提高系统的鲁棒性,同时结合动态面方法设计了面向大机动目标拦截的复合制导控制一体化方案。数字仿真结果证明了该方法的有效性。
1 模型阐述
1.1 制导控制一体化设计模型
在这部分中,建立了弹目视线坐标系下的具有严格反馈形式的三维制导控制一体化模型。
首先,拦截几何关系如图1所示。OxIyIzI,Mx4y4z4分别表示惯性坐标系和弹目视线(Lineofsight,LOS)坐标系;M(xm,ym,zm),T(xt,yt,zt)分别表示导弹和目标在惯性坐标系下的位置;R表示弹目相对距离;q1与q2分别表示弹目视线倾角与视线偏角。
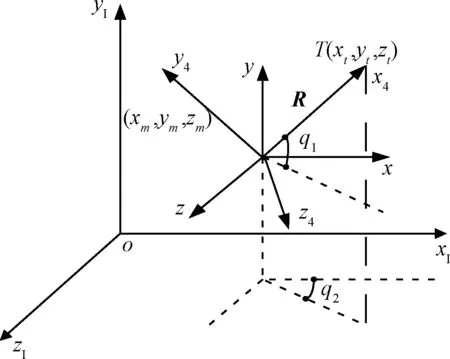
图1 三维拦截几何关系图Fig.1 Interception geometry in three dimensional space
在弹目视线坐标系中,根据科里奥利定理,弹目视线坐标系相对于惯性坐标系下的旋转角速度矢量Ω,弹目相对距离R,弹目相对速度VR与弹目相对加速度AR有如下关系
(1)
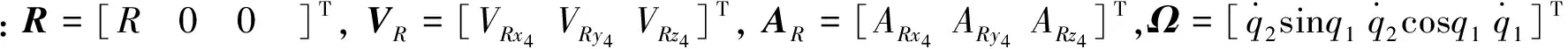
(2)
将式(1)展开,得到:
(3)
(4)
弹目相对加速度可表示为
(5)
式中:AT=[ATx4ATy4ATz4]T,AM=[AMx4AMy4AMz4]T,分别表示目标与导弹的加速度在弹目视线坐标系下的向量。根据科里奥利定理,导弹加速度在弹目视线坐标系下可以表示为
(6)
式中:VMx4,VMy4与VMz4表示导弹速度在弹目视线坐标系下的分量:
(7)
考虑到导弹的动力学方程
(8)
式中:m为导弹质量,Y与Z为导弹受到的空气动力,θ,ψv与γv分别为导弹的弹道倾角,弹道偏角与速度倾斜角。
假设1. 本文考虑的对象是STT导弹,在设计的控制律下,速度倾斜角可以很快收敛到零。所以,作出速度倾斜角近似为零的假设,即γv≈0。
将式(8),式(7),式(6),式(5)代入式(4)中,考虑到假设 1并适当化简,可得
(9)
假设2. 导弹的气动力以及气动力矩可以表示为
(10)
(11)
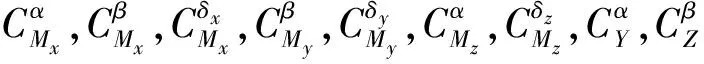
综合式(9)~(11),假设 1~2,以及导弹的转动方程,严格反馈的三维制导控制一体化模型
(12)

其中,
注1. 模型不需要假设导弹初始速度方向与弹目视线近乎平行,提高了模型的适用范围。
1.2 目标动态模型
本文的机动目标的动态模型为[20]
(13)
式中:xt,yt,zt为目标在惯性坐标系下的位置坐标,Vt表示目标的速度,θt,ψvt为目标的弹道倾角与偏角,at1,at2为目标在俯仰与偏航方向的机动[19]。
2 制导控制一体化设计与稳定性分析
面向大机动目标的拦截,结合有限时间收敛的扩张状态观测器、自适应控制方法与动态面控制方法,提出了一种复合制导控制一体化设计方案,并且证明了拦截过程中所有飞行状态的稳定性。
2.1 制导控制一体化设计
考虑到下面的一阶非线性动态系统
(14)
式中:x∈R为状态量,f(x)为已知函数,w(t)为未知总体不确定性,uz(t)为控制量。式(14)可以被扩张成为一个二阶动态系统
(15)
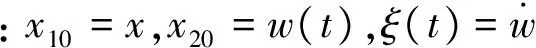
(16)
式中:e10=x10-z1,C(y)为S函数,用来替代符号函数,以减少观测器的抖震
(17)
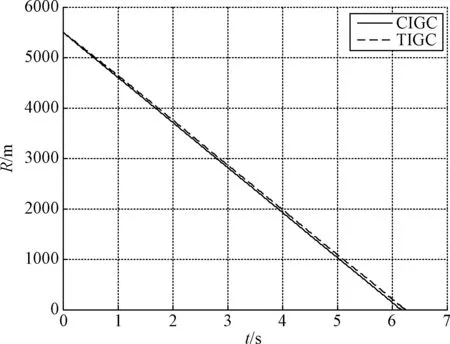
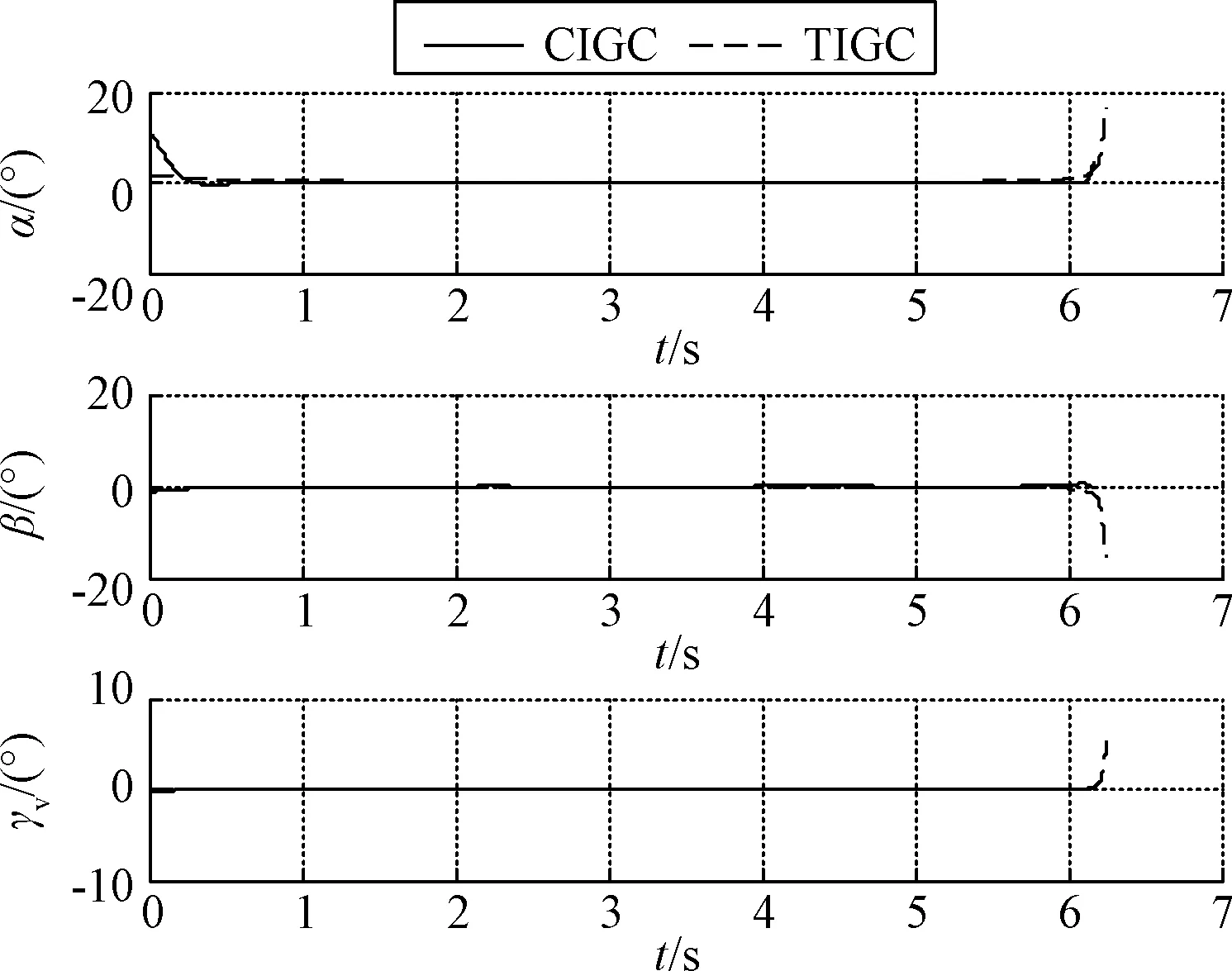
式中:e表示自然底数。根据文献[20],合理的选取设计参数kz01与kz02,满足ρ>1,0.5 (18) 注2. 根据文献[21],如果扩张状态观测器的估计误差满足有限时间收敛,则观测器设计满足分离原理,即观测器与控制器可以分开设计。式(16)形式的扩张状态观测器满足有限时间收敛,在文献[19]中已被证明,所以控制器与观测器的设计可以分开设计。 为了保证导弹直接拦截杀伤目标,根据平行接近法的原理,控制目标是将弹目视线倾角与偏角的导数控制到0。所以控制目标可表示为 (19) 饱和函数被引入来提高算法的控制性能 (20) 假设3. 控制系数矩阵g1(x1),g2(x2)都可逆,并且范数有界,系统状态变量与导弹弹道倾角是可以测量得到的。 1)定义第一个误差面e1 e1=x1-xd (21) 根据式(16),设计第一个扩张状态观测器估计不确定性d1 (22) (23) (24) (25) 2) 定义第二个误差面e2 (26) 设计第二个扩张状态观测器估计不确定性d2 (27) 式中:β21>0,β22>0。虚拟控制律设计为 (28) (29) 3) 定义第三个误差面e3 (30) 设计第三个扩张状态观测器估计不确定性d3 (31) 式中:β31>0,β32>0。给出系统的实际控制量 (32) (33) 式中:τ1>0,τ2>0,τ3>0,κ1=diag(κ11,κ12),κ2=diag(κ21,κ22,κ23),κ3=diag(κ31,κ32,κ33)。 注3. 采取的自适应律是为了对扩张状态观测器的观测误差进行补偿,提高系统控制精度与鲁棒性。 2.2 稳定性分析 定义误差变量如下所示 (34) (35) 由动态面方法中引入的一阶滤波器,可得 (36) 所以误差向量p1,p2的导数有 (37) 定义李雅普诺夫候选函数 (38) 对李雅普诺夫候选函数求导可得 (39) 根据式(12)与式(21)~(33),可得 (40) (41) (42) (43) 将式(37)、式(40)~(43)代入式(39),可得 (44) 根据文献[19],有限时间收敛的扩张状态观测器在合理选取参数后,zi2将在时间tz收敛到系统不确定性的一个邻域内,设扩张状态观测器的观测误差的上界为ηi(i=1,2,3)。所以,当i=1时,e1=[e11e12]T,η1=[η11η12]T,可得 η12e12tanh(e12/w) (45) 对于函数tanh(·),有 (46) 根据式(46),式(45)可进一步写为 0.2785w(η11+η12) (47) 同理可得,当i=2,3,有 0.2785w(ηi1+ηi2+ηi3) (48) 根据Young不等式,可得 (49) 将式(47)~(49)代入式(44),可得 (50) 式中:I为相应的单位矩阵,H为常数 (51) 选取控制参数满足条件 (52) 式中:μ>0,μ∈R。可得 (53) 求解式(53),可得 (54) 注 4. 在制导控制一体化设计中,有限时间收敛的扩张状态观测器可以有效地观测目标的加速度不确定性以及其他总体不确定性;使用自适应控制律对扩张状态观测器的观测误差进行补偿,以提高系统的鲁棒性与控制性能。 仿真参考值见表1。实际仿真模型的参数摄动最大值选为±20%。机动目标的初始位置为(3000m,3500m,3000m),目标速度为Vt(0)=100 m/s,目标机动为at1=55sin(3t) m/s2,at2=55sin(3t) m/s2;导弹的初始位置为(0m,0m,0m),导弹初始姿态角与初始三轴角速度分别设为零,导弹的初始速度为Vt(0)=800 m/s。 扩张状态观测器参数为β11=β21=β31=100,β12=β22=β32=10000,ρ1=0.8,ρ2=2ρ1-1,α1=1/ρ1,α2=1/ρ1+ρ1-1,kz1=150,kz2=5000。自适应控制律参数为w=1,κ1=diag(0.15,0.12),κ2=diag(0.2,0.2,0.1),κ3=diag(0.3,0.8,0.6),τ1=1,τ2=1.5,τ3=3。控制参数为 k1=diag(8,4),kb1=diag(0.01,0.01),σ1=diag(0.001,0.001,0.01),k2=diag(10,20,20),kb2=diag(0.01,0.01,0.01),k3=diag(10,15,10),σ2=diag(0.001,0.001,0.001),kb3=diag(0.01,0.01,0.01)。 为了验证本文提出的复合制导控制一体化设计(Compositeintegratedguidanceandcontrol,CIGC)的有效性,使用传统的基于动态面的制导控制一体化方法(Traditionalintegratedguidanceandcontrol,TIGC)做对比。考虑迎头拦截的场景,为了验证模型的有效性,选取导弹不同的初始弹道倾角与弹道偏角,目标的初始弹道倾角与弹道偏角为θt(0)=-35°,ψvt(0)=135°,仿真结果如表2所示。取其中一组拦截场景,导弹的初始弹道倾角与弹道偏角为θ(0)=10°,ψv(0)=-35°。仿真结果如图2~6所示。 图2 CIGC拦截轨迹Fig.2 Interception trajectory of CIGC 图3 TIGC拦截轨迹Fig.3 Interception trajectory of TIGC 由表2的仿真结果表明,CIGC相比TIGC脱靶量更小,拦截时间更短,在不同的初始弹道倾角与弹道偏角条件下,均能拦截大机动目标,证明了所提出设计模型不需要假设导弹速度矢量和弹目视线近似重合。当导弹的初始弹道倾角与弹道偏角为θ(0)=10°,ψv(0)=-35°时,CIGC的脱靶量为0.4419m,拦截时间为6.169s;TIGC的脱靶量为3.2011m,拦截时间为6.248s,CIGC脱靶量更小,可以实现较高精度的大机动目标拦截,TIGC缺少对不确定性的处理,影响了制导精度。 从图 2~3可以看出,CIGC与TIGC的拦截弹道,可以看到采用相同制导策略的两种方法弹道差别不大;从图4可以看出,CIGC有更小的脱靶量与拦截时间;图5~6表明,导弹的状态平稳,并且速度倾斜角很快收敛到零,说明了假设 1的合理性。 图4 弹目相对距离Fig.4 Relative distance 图5 攻角、侧滑角与速度倾斜角曲线Fig.5 Curves of attack angle, side slip angle and velocity bank angle 图6 滚转、偏航与俯仰舵面控制量曲线Fig.6 Curves of aileron, rudder and elevator deflections 本文针对大机动目标的拦截问题,建立了适用范围更广的STT导弹的三维制导控制一体化设计模型并结合有限时间收敛的扩张状态观测器与自适应动态面控制方法提出了复合制导控制一体化设计方案,有效地实现了在目标机动加速度未知以及各种不确定性影响的情况下对大机动目标的精确拦截。 表1 仿真参数 表2 仿真结果 [1] 方群, 陈武群, 袁建平. 一种抗干扰修正比例导引律的研究[J]. 宇航学报, 2000, 21(3): 76-81. [FangQun,ChenWu-qun,YuanJian-ping.Astudyonthemodifiedproportionalguidanceofinterference-proof[J].JournalofAstronautics, 2000,21(3):76-81.] [2]WilliamsDE,RichmanJ,FriedlandB.Designofanintegratedstrapdownguidanceandcontrolsystemforatacticalmissile[J].AIAAPaper83-2169, 1983. [3]YanH,JiH.Integratedguidanceandcontrolfordual-controlmissilesbasedonsmall-gaintheorem[J].Automatica, 2012, 48(10): 2686-2692. [4]ZhaoCZ,HuangY.ADRCbasedintegratedguidanceandcontrolschemefortheinterceptionofmaneuveringtargetswithdesiredLOSangle[C].Proceedingsofthe29thChineseControlConference,IEEEPubl.,Piscataway,NJ, 2010: 6192-6196. [5] 查旭, 崔平远, 常伯俊. 攻击固定目标的飞行器制导控制一体化设计[J]. 宇航学报, 2005, 26(1): 13-18. [ZhaXu,CuiPing-yuan,ChangBo-jun.Anintegratedapproachtoguidanceandcontrolforaircraftapplyingtoattackthegroundfixedtargets[J].JournalofAstronautics, 2005, 26(1): 13-18.] [6] 舒燕军, 唐硕. 轨控式复合控制导弹制导与控制一体化反步设计[J]. 宇航学报, 2013, 34(1): 79-85. [ShuYan-jun,TangShuo.IntegratedguidanceandcontrolbacksteppingdesignforblendedcontrolmissilebasedonNDO[J].JournalofAstronautics, 2013, 34(1): 79-85.] [7] 董飞垚, 雷虎民, 李炯, 等. 拦截弹自适应最优滑模制导和控制一体化设计[J]. 宇航学报, 2013, 34(11): 1456-1461. [DongFei-yao,LeiHu-min,LiJiong,etal.Designofintegratedadaptiveoptimalsliding-modeguidanceandcontrolforinterceptor[J].JournalofAstronautics, 2013, 34(11): 1456-1461.] [8]HouMZ,LiangXL,DuanGR.Adaptiveblockdynamicsurfacecontrolforintegratedmissileguidanceandautopilot[J].ChineseJournalofAeronautics, 2013, 26(3): 741-750. [9]XinM,BalakrishnanSN,OhlmeyerEJ.Integratedguidanceandcontrolofmissileswithθ-Dmethod[J].IEEETransactionsonControlSystemsTechnology, 2006, 14(6): 981-992. [10]GuoC,LiangXG.Integratedguidanceandcontrolbasedonblockbacksteppingslidingmodeanddynamiccontrolallocation[J].ProceedingsofInstitutionofMechanicalEngineers,PartG:JournalofAerospaceEngineering, 2015, 229(9): 1559-1574. [11] 周军, 王婷. 基于二阶滑模控制的驾束制导导弹一体化制导系统设计[J]. 宇航学报, 2007, 28(6): 1632-1637. [ZhouJun,WangTing.Integratedguidance-controlsystemforbeam-ridingguidancemissilesbasedonsecondorderslidingmodecontrol[J].JournalofAstronautics, 2007, 28(6): 1632-1637.] [12]WangWH,XiongSF,WangS.Threedimensionalimpactangleconstrainedintegratedguidanceandcontrolformissileswithinputsaturationandactuatorfailure[J].AerospaceScienceandTechnology, 2016, 53: 169-187. [13]ZhurbalA,IdanM.Effectofestimationontheperformanceofanintegratedmissileguidanceandcontrolsystem[J].AerospaceandElectronicSystems,IEEETransactionson, 2011, 47(4): 2690-2708. [14] 刘晓东, 黄万伟, 禹春梅. 含扩张状态观测器的高超声速飞行器动态面姿态控制[J]. 宇航学报, 2015, 36(8): 916-922. [LiuXiao-dong,HuangWan-wei,YuChun-mei.Dynamicsurfaceattitudecontrolforhypersonicvehiclecontainingextendedstateobserver[J].JournalofAstronautics, 2016, 37(8): 936-945.] [15] 刘志新, 游秀, 杨洪玖,等. 基于扩张状态观测器的空间飞网捕捉系统参数估计[J]. 宇航学报, 2014, 35(2): 200-206. [LiuZhi-xin,YouXiu,YangHong-jiu,etal.Theparameterestimationbasedonextendedstateobserverforspacenetcapturesystem[J].JournalofAstronautics, 2014, 35(2): 200-206.] [16] 孙向宇, 晁涛, 王松艳, 等. 考虑通道耦合因素的制导控制一体化设计方法[J]. 宇航学报, 2016, 37(8): 936-945. [SunXiang-yu,ChaoTao,WangSong-yan,etal.Integratedguidanceandcontroldesignmethodconsideringchannelcoupling[J].JournalofAstronautics, 2016, 37(8): 936-945.] [17]RanMP,WangQ,HanDL,etal.Backsteppingdesignofmissileguidanceandcontrolbasedonadaptivefuzzyslidingmodecontrol[J].ChineseJournalofAeronautics, 2014, 27(3): 634-642. [18] 齐辉, 张泽, 许江涛, 等. 基于Nussbaum增益滑模自适应控制的导弹制导控制一体化设计[J]. 控制与决策, 2017, 32(1): 93-99. [QiHui,ZhangZe,XuJiang-tao,etal.IntegratedguidanceandcontrolofmissilebasedonNussbaumgainadaptiveslidingmodecontrolmethod[J].ControlandDecision, 2017, 32(1): 93-99.] [19]XiongSF,WangWH,LiuXD,etal.Anovelextendedstateobserver[J].ISATransactions, 2015,58: 309-317. [20]DwivediPN,TiwariSN,BhattacharyaA,etal.AZEMbasedeffectiveintegratedestimationandguidanceofinterceptorinterminalPhase[J].ISATransactions,2015,58:309-317. [21]SunGF,RenXM,ChenQ,etal.Amodifieddynamicsurfaceapproachforcontrolofnonlinearsystemswithunknowninputdeadzone[J].InternationalJournalofRobustandNonlinearControl, 2015, 25: 1145-1167. 通信地址:北京航空航天大学自动化科学与电气工程学院新主楼E区(100191) 电话:(010)82338658 E-mail:dlmu_it_lc@163.com 王卫红(1968-),女,博士,教授,主要从事制导控制一体化,系统仿真,高精度运动控制等研究。本文通信作者。 通信地址:北京航空航天大学自动化科学与电气工程学院新主楼E区(100191) 电话:(010)82338597 E-mail:wwh2005@buaa.edu.cn Integrated Guidance and Control Design Against Highly Maneuvering Target LAI Chao1, WANG Wei-hong1, XIONG Shao-feng2 (1. School of Automation Science and Eletrical Engineering, Beihang University, Beijing 100191, China; 2. System Design Department, Second Academy of China Aerospace Science & Industry Corporation, Beijing 100854, China) A composite control method combining the finite-time stable nonlinear extended state observer (ESO) and the adaptive dynamic surface control is applied to the integrated guidance and control (IGC) for a skid-to-turn (STT) missile against a highly maneuvering target. Firstly, a new three-dimensional integrated guidance and control design model for a skid-to-turn missile is established with fewer assumptions. Next, a nonlinear ESO with the finite time convergence performance is introduced to estimate the uncertainties including the unknown target accelerations. And then, the adaptive control law is introduced to compensate the error of the extended state observer. Based on the nonlinear ESO, adaptive technique and dynamic surface control (DSC), a composite IGC scheme is proposed. The stability of the system is guaranteed by the Lyapunov stability theory. And the numerical simulations demonstrate the improvements on the hitting performance of the proposed control scheme. Integrated guidance and control (IGC); Uncertainty; Dynamic surface control (DSC); Adaptive control; Extended state observer (ESO) 2017-04-06; 2017-05-19 TJ765 A 1000-1328(2017)07-0714-09 10.3873/j.issn.1000-1328.2017.07.000 赖 超(1990-),男,博士生,主要从事制导控制一体化方向的研究。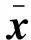


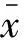
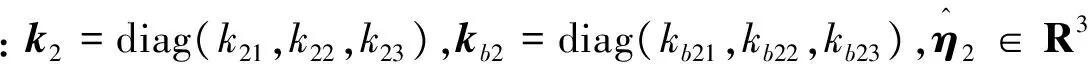

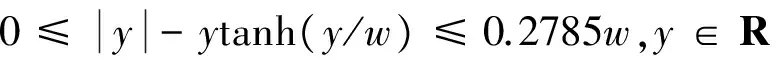
3 仿真校验


4 结 论