火炮武器拦截钻地弹有效命中概率计算方法

王海川，徐国亮

（江苏自动化研究所，江苏 连云港 222006）

0 引言

出于对地面和地下坚固目标的打击需求，钻地武器成为世界各国武器装备研发的重点［1-2］。钻地武器俗称钻地弹，通常是指携带侵彻战斗部，用于对地下指挥中心、导弹发射井、武器库、机场跑道等地面加固目标和地下设施进行攻击的对地攻击弹药。对钻地武器的研制，美国一直走在前列［3-4］。美国空军装备的GBU-57 系列重型钻地弹最为典型。

GBU-57 重型钻地弹是目前威力最强的钻地弹药之一，主要由美空军B-2A 或B-52 轰炸机搭载，如下页图1 所示，投弹方式为飞抵目标附近上空投掷，投放高度10 km 以上，飞行速度300 m/s～500 m/s，末端采用高角俯冲攻击方式。GBU-57 重型钻地弹长度为6.25 m，直径为800 mm，弹重13 600 kg，装药量约2 400 kg，采用整体式动能侵彻战斗部，战斗部弹体采用了更坚固、更耐高温耐冲击的镍钴合金或合金钢以增加钻地爆炸效果，对钢筋混凝土侵彻能力超过60 m［5-6］。

图1 B-2A 隐身飞机搭载的GBU-57 钻地弹

根据钻地弹特性分析可知，钻地弹重量大、惯性大、壳体壁厚大，弹头和弹体通常采用高强度、高韧性的合金钢材料［7］，头部壳体厚度超过400 mm，现有火炮穿甲弹难以从头部正面直接贯穿。现有小口径防空炮弹拦截导弹战斗部壳体前端厚度为40 mm 左右［8-9］，对厚度为110 mm 左右的GBU-57重型钻地弹侧壁，很难直接穿透造成有效毁伤（如脱壳穿甲弹、预制破片弹），或通过爆炸冲击波或直接碰撞使其偏离其预定落点（如杀伤爆破弹）。

埋头弹作为一种新型弹种近年来得到快速的发展。埋头弹采用两级点火，底火被击发后，辅助发射药燃烧并将弹丸推离药筒，推入弹膛；弹丸脱离药筒后，辅助发射药火焰随即引燃主装药，火药燃烧产生的气体推动弹丸高速飞离身管，使埋头弹具有更高的炮口初速和穿甲能力。如英国BAE 系统公司研制的CT-40 型埋头弹火炮系统中的尾翼稳定脱壳穿甲弹，炮口初速高达1 640 m/s，据称能在1 500 m 处垂直击穿150 mm 厚均质装甲板。40 mm埋头弹内部结构和穿甲效果如图2 所示［10-11］。从目前的情况来看，40 mm～45 mm 埋头弹可以在1 500 m距离击穿150 mm～200 mm 的钢装甲［12］，这为使用火炮武器在1 000 m 近程范围内穿透钻地弹侧壁，进而摧毁钻地弹提供了可行性。

图2 CT-40 型40 mm 埋头弹内部结构和穿甲效果图

由于钻地弹中战斗部占比较大，内部装有大量炸药，因此，在埋头弹具备高初速和高穿甲能力的基础上，如果在埋头弹内部再添加含能材料［13］，使其能够在穿透壳体厚度相对较小的钻地弹侧壁壳体后在其内部爆燃，引爆其内部炸药，则可采用“直接贯穿+燃爆”的方式对钻地弹实施有效毁伤。

钻地弹的高角俯冲弹道与常规巡航导弹存在差异，但其侧视面积相对常规巡航导弹的截面积要大一个数量级以上，末端攻击速度仅为1.2 Ma 左右，现有的防空火炮武器系统对其捕获、跟踪和瞄准都不存在技术问题。埋头弹能否在近距命中和穿透钻地弹壳体，是火炮是否具备拦截钻地弹能力的关键所在，因此，在论证火炮武器系统拦截钻地弹的可行性时，首先要进行命中概率和毁伤概率的计算分析。

命中概率是在给定的射击条件下命中目标的可能性的量度。传统火炮武器系统在计算对空中目标的命中概率时，通常只考虑弹目相遇时目标是否命中的问题［14-15］，但是，在拦截钻地弹类大壁厚弹药时，火炮武器系统还须增加考虑是否能穿透其厚壁壳体的问题。为此，在此提出了一个“有效命中概率”的概念。所谓有效命中概率指的是在给定的射击条件下命中目标，且穿透其防护壳体的可能性的量度，它是在命中概率概念上的扩展。对于钻地弹类大壁厚弹药，炮弹单纯的命中而无法穿透其防护壳体是没有意义的，只有在炮弹穿透其防护壳体实现“有效命中”后，才能具有破坏结构、爆燃引爆等后续毁伤能力。即使炮弹的千米穿甲能力能保证在千米距离上垂直穿透钻地弹的壳体，但是如果炮弹在空中与目标相遇时弹目交会角过小，会导致炮弹难以斜穿透钻地弹的壳体，甚至产生跳弹，因此，弹目交会角的大小对于能否实现“有效命中”有着至关重要的影响，也是本文研究分析的重点。

本文在常规火炮对空中目标命中概率计算方法的基础上，通过增加炮弹穿甲能力和最小弹目交会角等约束条件，提出对钻地弹类大壁厚弹药的有效命中概率的计算方法，并对影响弹目交会角的多种因素进行分析，以为火炮武器系统拦截钻地弹的可行性论证提供技术参考。

1 弹目交会角计算模型

弹目交会角计算原理图如下页图3 所示，其中，火炮阵地布放在防护点的正北方向。

在图3 中：

图3 拦截钻地弹时弹目交会角计算原理图

1）A 点为钻地弹，O 点为防护中心点，AO 为钻地弹距防护点斜距离，设为D0，此处假定钻地弹在末端以俯冲角ε 直线攻击，忽略重力和弹道末端制导控制等因素引起的攻击段弹道弯曲；

2）C 点为火炮布放点，AC 为火炮射击距离，设为D。由于埋头弹速度较高，此处假定火炮发射的弹丸近似按直线飞行，同时忽略弹丸攻角和重力、气象等因素引起的弹丸俯仰角变化量；

3）β 为钻地弹目标方位角，Y 轴指向正北方向；

4）α 为炮弹与钻地弹相遇时的弹目交会角；

5）OC 为火炮阵地与防护点的水平距离，即布放间距，设为d。

在△AOC 和△BOC 中，依据余弦定理可得：

式（7）为求解弹目交会角的近似数学公式，需要补充的是：在α 大于90°时，要另行处理。

2 弹目交会角的影响要素分析

在分析采用高速穿甲弹，如埋头弹，拦截钻地弹的可行性时，首先要确定其穿甲能力。由于高速穿甲弹是否能够穿透钻地弹的壳体，主要取决于弹丸的穿甲能力和弹目交会角，而高速穿甲弹出炮口后，随着弹丸存速的降低，其穿甲能力也在减弱。因此，需要事先知道高速穿甲弹不同射距情况下的90°等效穿透钢板厚度（与钻地弹壳体材料刚度等效），这样就可以求出不同射距处可穿透钻地弹壳体的最小弹目交会角。如假定：埋头弹的90°等效穿透厚度在1 000 m 射距处为180 mm，在1 500 m 射距处为150 mm，重型钻地弹的壳体壁厚为110 mm，轻型钻地弹的壳体壁厚为50 mm，那就可以求出对应不同射程的垂直穿甲能力，进而求出穿透不同壳体厚度所需的最小弹目交会角；此外，考虑弹目交会时弹丸跳弹因素，须再增加一个弹丸不跳弹限制角（假定为15°），如图4 所示。

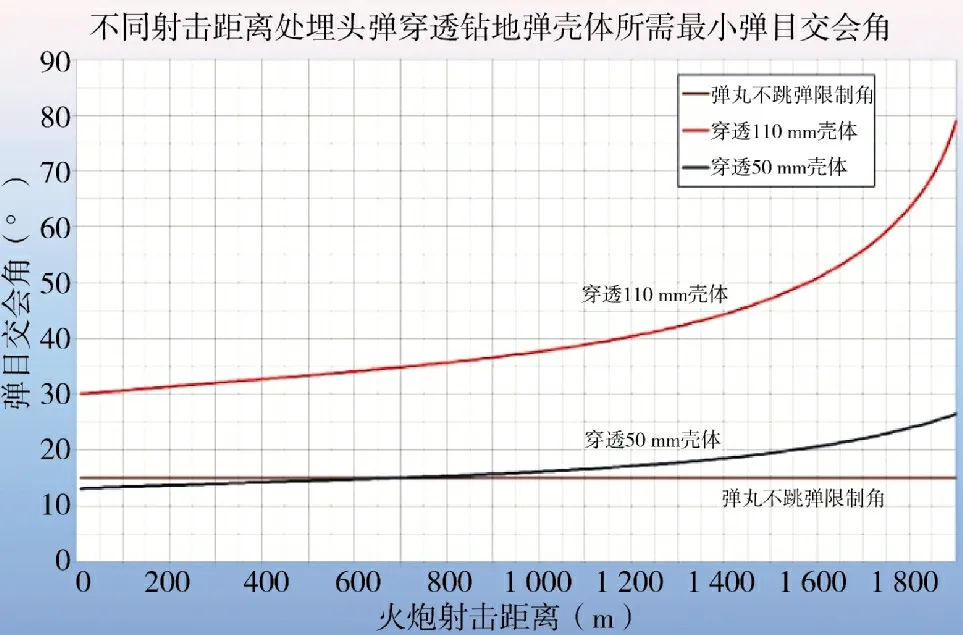
图4 不同射击距离处埋头弹穿透钻地弹壳体所需最小弹目交会角

如图4 所示，在1 000 m 射距处，对壳体壁厚为110 mm 的重型钻地弹，穿透其壳体的最小弹目交会角为37.7°；而对壳体壁厚为50 mm 的轻型钻地弹，穿透其壳体的最小弹目交会角为16.2°。穿透轻型钻地弹壳体所需的最小弹目交会角，在射程小于700 m后小于弹丸不跳弹限制角，在此情况下，最小弹目交会角应为弹丸不跳弹限制角。

由式（7）可以看出，弹目交会角与钻地弹来袭方位角、末端俯冲角、火炮射击距离和火炮阵地布放间距4 个主要因素有关，下面将对这4 个因素的影响程度分别加以分析。考虑到实际应用条件，钻地弹来袭方位角范围设为0°～360°；钻地弹俯冲角范围设为50°～90°；防空火炮有效射程范围设为1 500 m～200 m；火炮阵地与防护点的布放间距的范围设为200 m～700 m。

2.1 不同火炮布放间距对弹目交会角的影响

根据前面所求取的弹目交会角计算公式，可在火炮阵地部署在防护点正北方向、重型钻地弹来袭方位角为45°和末端俯冲角为60°情况下，并考虑埋头弹穿透壳体所需最小弹目交会角因素，求取火炮不同部署半径情况下，弹目交会角与射击距离或钻地弹距防护点距离的关系曲线，如下页图5 所示。

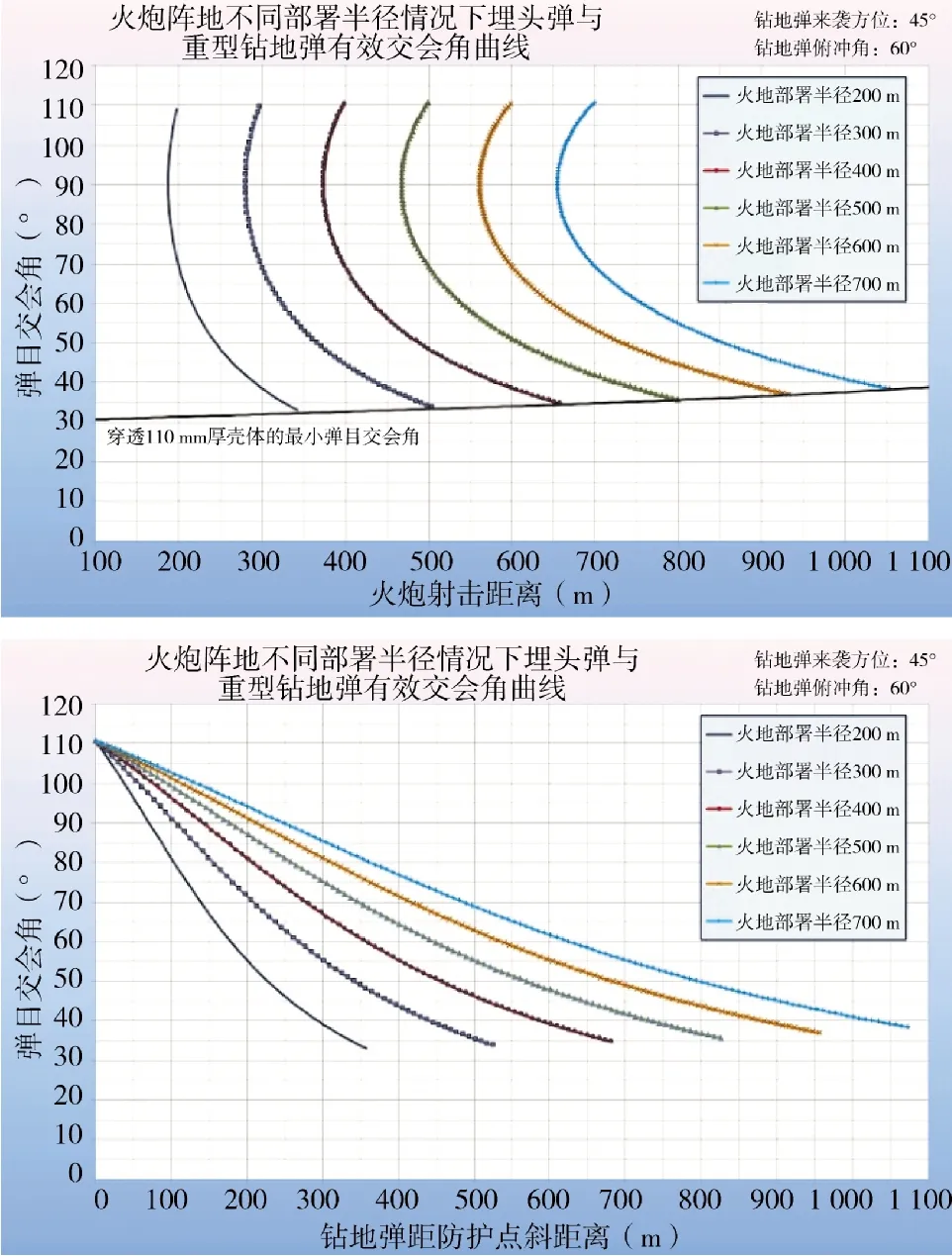
图5 火炮阵地不同部署半径情况下埋头弹与重型钻地弹弹目交会角曲线

由图5 可以看出，随着火炮阵地部署半径的逐渐增加，火炮有效射击距离逐渐变远，导致炮弹的单发命中概率逐渐降低，不利于全航路命中概率的提高，但是钻地弹距防护点的可拦截区段逐渐变大（拦截时间变长），导致可射击的弹数增多，这有利于全航路命中概率的提高，因此，火炮阵地部署问题可归纳为一个以全航路有效命中概率为目标函数的优化问题。

2.2 不同钻地弹来袭方位角对弹目交会角的影响

在火炮阵地部署在防护点正北方向、部署半径为400 m 和钻地弹末端俯冲角为60°情况下，可求取出不同钻地弹来袭方位角所对应的弹目交会角与射击距离的关系曲线，如图6 所示。

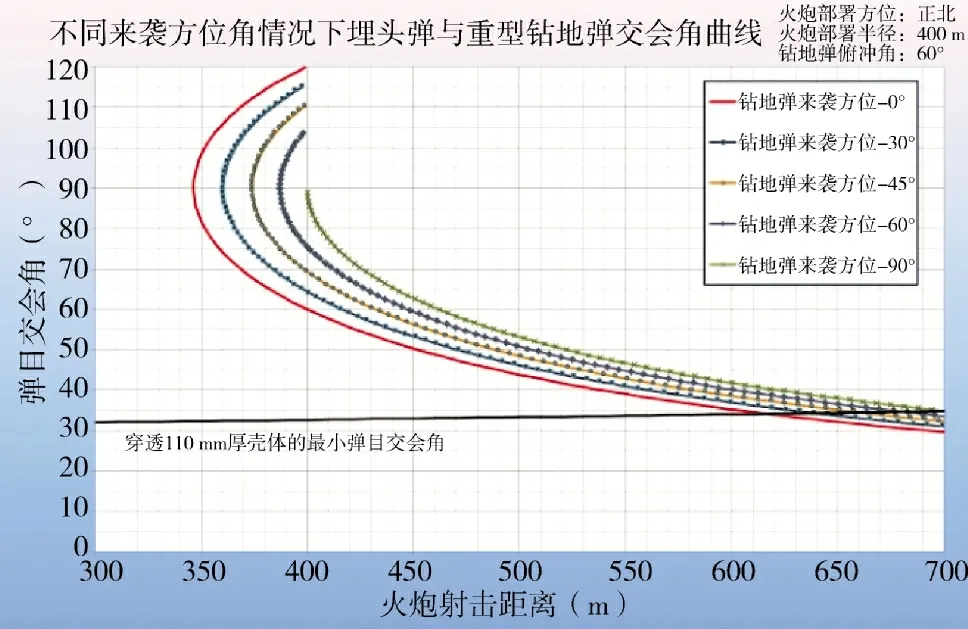
图6 不同来袭方位角情况下埋头弹与重型钻地弹交会角曲线

从图6 可以看出，钻地弹来袭方位角从0°增加到90°，会导致与弹目交会角对应的最远有效拦截距离从610 m 增大到近700 m，但是最近有效拦截距离也从350 m 增大到400 m，拦截区段的变远会导致全航路命中概率的下降。

2.3 不同钻地弹俯冲角对弹目交会角的影响

在火炮阵地部署在防护点正北方向、部署半径为400 m 和钻地弹来袭方位角为45°情况下，可求取出不同钻地弹俯冲角所对应的弹目交会角与射击距离的关系曲线，如图7 所示。

图7 不同钻地弹俯冲角情况下埋头弹与重型钻地弹弹目交会角曲线

从图7 可以看出，钻地弹俯冲角从50°增加到90°，会导致与弹目交会角对应的最大有效拦截距离从620 m 增大到700 m，但是最近拦截距离也从350 m 增大到400 m，拦截区段的变远会导致系统命中概率的下降。

3 系统有效命中概率计算方法与计算结果分析

传统火炮对空中目标命中概率的计算，可参照相关国军标中的对空射击效力计算方法进行，但是，在计算系统有效命中概率时，需要增加与炮弹穿甲能力相关的最小弹目交会角或者弹丸不跳弹限制角的约束条件，具体步骤为：

1）按照传统的火炮武器系统命中概率计算方法，计算出炮弹的单发命中概率；

2）根据对应的火炮发射阵位和目标位置，计算出该发炮弹的弹目交会角。当计算出的弹目交会角小于最小弹目交会角或者弹丸不跳弹限制角时，该发炮弹的单发命中概率清零，即该发炮弹无法穿透大壁厚弹药的壳体，将不参与全航路命中概率的统计；

3）将所有弹目交会角大于最小弹目交会角或者弹丸不跳弹限制角的每发炮弹的单发命中概率，进行全航路命中概率的统计，所得结果即为系统全航路有效命中概率。在此基础上，可根据毁伤钻地弹所需有效命中弹数，求出系统全航路毁伤概率。

为进行系统对重型钻地弹有效命中概率的计算，假定相关计算参数如下：

·火炮射速：3 000 发/min

·射弹数：60 发

·拦截近界：200 m

·火炮部署半径（火炮阵地距防护点的距离）：300 m～700 m

·火炮有效射程：最大1 500 m

·系统瞄准精度：系统误差（m）2.0 mrad，随机误差（σ）3.0 mrad

·钻地弹末端飞行速度：400 m/s

·重型钻地弹参数：直径800 mm，侧壁等效长度

5.5 m，壳体厚度110 mm

·埋头弹千米90°等效穿甲厚度：180 mm

根据以上设定参数，计算求取的火炮武器系统对重型钻地弹的不同来袭方位和不同火炮阵地部署半径的全航路有效命中概率如图8 所示。由图8可见，在重型钻地弹俯冲角为60°的情况下，单门火炮在火炮部署方向（正北）附近具有较高的全航路有效命中概率，但在目标来自正南方向时，全航路有效命中概率下降到最低。随着火炮部署半径从300 m 逐渐增加到700 m，全航路有效命中概率也逐渐降低。

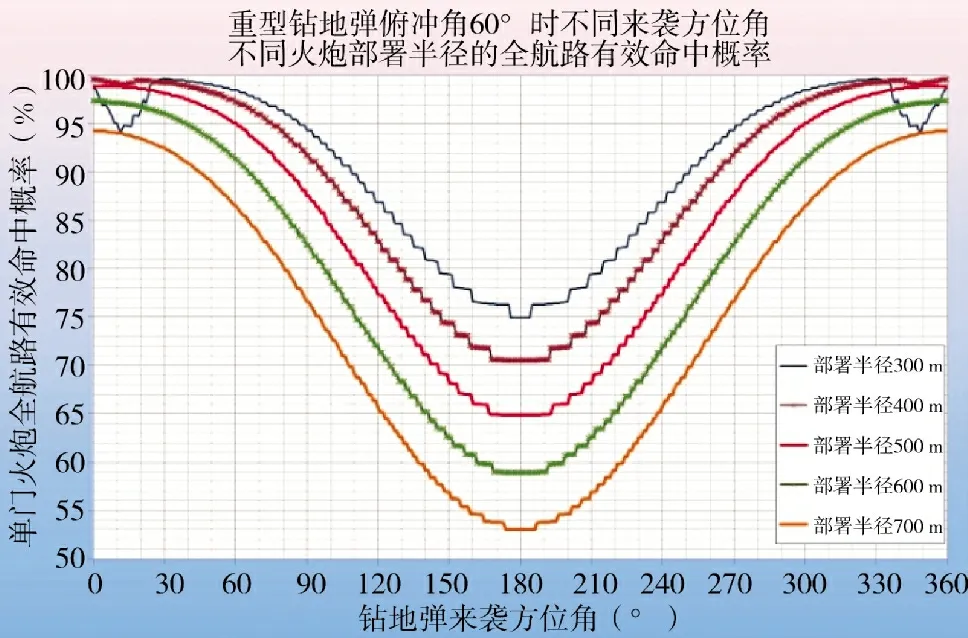
图8 不同钻地弹方位和火炮部署半径情况下的单炮全航路有效命中概率

为提高火炮武器系统对重型钻地弹的全方位拦截能力，须采用多炮集火方式，为此按照两门火炮在防护点南、北方向，相同部署半径的配置方式，计算出的对重型钻地弹不同来袭方位和不同火炮阵地部署半径的全航路集火毁伤概率如图9 所示。

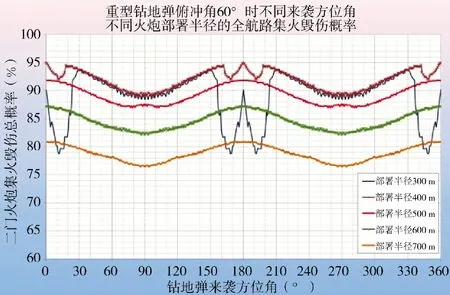
图9 不同钻地弹方位和火炮部署半径情况下的双炮全航路毁伤概率

从图9 可以看出，在钻地弹俯冲角为60°的情况下，两门火炮的全航路集火毁伤概率（有效命中2发为毁伤）在部署半径为400 m 时大于88 %，具备了较高的拦截毁伤能力，同时也表明了火炮武器系统拦截重型钻地弹的可行性。对于防护要求很高的重要设施，通过进一步增加火炮数量和优化阵地配置，可以得到更高的全方位集火拦截毁伤能力。采用这种计算方法，可以对不同钻地弹、不同俯冲角、不同炮弹穿甲能力、不同火炮数量和配置方式，及部署半径、不同拦截近界和射弹数等多种情况进行全面分析和系统配置及部署优化设计。

4 结论

随着火炮发射的高速穿甲弹，如埋头弹等技术的发展和穿甲能力的提升，使用火炮发射的高速含能穿甲弹，通过“直接贯穿+ 燃爆”方式，对钻地弹类大壁厚弹药实施拦截，可为要地或重要设施对钻地弹类大壁厚弹药的防御提供一种现实可行的手段。本文主要针对地面火炮武器末端拦截大壁厚钻地弹的作战需求，在常规火炮对空中目标命中概率计算方法的基础上，提出了“有效命中概率”概念，对影响弹目交会角的多种因素进行了分析，给出了增加炮弹穿甲能力和弹目交会角等约束条件的有效命中概率计算方法，可为火炮武器系统拦截钻地弹的可行性论证提供技术参考。