脉冲推力最优轨迹的Hamilton边值问题

沈红新

(西安卫星测控中心宇航动力学国家重点实验室，西安 710043)



脉冲推力最优轨迹的Hamilton边值问题

沈红新

(西安卫星测控中心宇航动力学国家重点实验室，西安 710043)

针对大推力航天器的Hamilton边值问题(HBVP),提出一组基于变分法的通用方程，其中内点和其它端点(包括始、末端点)可以满足统一的方程形式，由此反映了更本质的边值条件解析结构。具体问题的最优性必要条件均可以从本文给出的通用方程中较方便地推出，避免了以往构造边值问题复杂繁琐的困难。仿真结果表明，本文方法可以保证有效、快速地获得大推力航天器的最优飞行路径。

边值问题; 最优性；内点；脉冲轨道

0 引 言

航天任务的经济、技术可行性和航天器飞行路径密切相关，最小化燃料和时间资源的消耗是航天器设计者不懈的追求，因此有效的优化控制方法对任务设计和方案制定至关重要。很多航天任务特别是载人任务都采用大推力的化学推进，为此，本文研究大推力航天器的最优飞行路径问题。目前，在非线性最优控制领域主要有两大类数值方法：直接法和间接法[1-3]。直接法一般采用参数化方法将连续空间的非线性最优控制问题转换成离散空间的非线性规划问题，虽然它具有容易实现和收敛半径较大的优点，但是直接法不能保证所获得解的最优性。相对地，间接法主要是构造和求解由最优控制的一阶必要条件得到的Hamilton边值问题(Hamilton boundary value problem,HBVP)[3-4]，其优点是：1)构造边值问题而不是参数优化问题，理论上能够准确快速获得最优解；2)由于采用最优控制理论(这里主要指变分法和极大值原理)，间接法能够提供优化问题必要的理论信息。但间接法也有其缺点：获得最优性条件的过程复杂繁琐，而且收敛半径较小[3]。

最优飞行路径确定的核心问题是构造和求解HBVP。近年来有很多研究集中于对HBVP的求解并产生了一批研究成果，如辛方法[5]、生成函数方法[6]、同伦变换[7-9]和微分变换[10]等，但这些研究都较少关注HBVP的构造方法。针对HBVP确立最优性条件复杂繁琐的缺点，本文的目的是以比较简洁的方程形式给出大推力航天器最优路径规划的通用模型，为该类问题最优性条件的建立提供统一的理论框架，这将有助于设计者快速、方便地构造进而求解HBVP。在任务初步设计阶段，大推力一般被假设为瞬时脉冲作用，因此大推力航天器最优路径确定是典型的含有内点约束的最优控制问题。Bryson和Ho[4]以及Lawden[11]研究了状态不连续内点约束最优控制问题，但他们的研究仅给出了内点处的最优性条件。本文将对内点和其它一般端点(例如初始时刻、终端时刻等)给出统一的边值问题模型，这样做的好处是得到的边界条件更具有一般性，可以方便确定起始时刻t0+和终端时刻tf-，而这两个时刻在轨迹优化问题中也可能是未知量 (例如自由终端时刻的问题)；相对地，Bryson和Ho[4]以及Lawden[11]的理论只适用于固定时间轨道转移或交会问题。

1 问题提出

由于化学推进的推力很大，发动机工作时间相对飞行时间来说很短甚至可以忽略，所以可假设化学推进的推力为瞬时脉冲，脉冲作用前后航天器位置连续而速度发生跳变，脉冲作用点之间由无动力滑行轨迹联接。无动力滑行轨迹满足如下动力学系统微分方程：

(1)

式中：x为状态变量，t为自变量(本文中自变量为时间)。需要指出的是，这里脉冲并不作为控制变量，而只是作为状态间断来考虑，所以在脉冲轨迹最优控制中不存在控制变量。

在轨迹初始点和终点之间如果存在状态或控制不连续，或者存在约束，这样的位置被称为内点，在内点处需要给出对应的最优性必要条件。比较方便的做法是将轨迹根据内点划分为多段，例如第j段从t(j-1)+开始到tj-结束，对应的状态分别是x(j-1)+和xj-，其中j-和j+分别代表在点j之前和之后。脉冲轨迹由于存在速度状态的突变，所以是典型的含有内点约束问题。在轨迹始末两个端点和内点施加非线性约束条件，这些约束用一个函数ψ描述，其表达式写为

ψ(x(j-1)+,xj-,t(j-1)+,tj-)=0,j=1,…,f

(2)

从容许函数类中求一函数x(t)，使泛函

J=φ(x(j-1)+,xj-,t(j-1)+,tj-),j=1,…,f

(3)

取极大(小)的问题常称为Mayer问题，它是古典变分的三个基本问题之一。此外还有Bolza问题和Lagrange问题。引进某些辅助变量可使三类问题互相转化。因此，研究三种基本问题中的任何一种都具有普遍意义，本文采用Mayer形式来定义优化问题。此外，通过改变目标函数的数学形式，求泛函极小的问题可以转化为求泛函极大的问题，而本文只考虑求极大值的问题。

对不同优化指标及约束条件的问题，HBVP确立最优性条件比较复杂繁琐[3]，本文的目的是为脉冲转移这类问题最优性条件的建立提供简洁的统一的理论框架，这将有助于设计者快速、方便地构造进而求解HBVP。

2 Hamilton边值问题构造的一般形式

变分法一般从推演泛函极值的必要条件开始。 因为式(3)表示的性能指标与约束条件或微分方程无关， 故引入和边界条件相联系的Lagrange乘子μ， 以及和微分方程相联系的协变量λ， 从而构造新的泛函J*：

(4)

(5)

从物理意义的角度说，只用时间和状态对这个泛函进行微小扰动，如果扰动的结果是这个泛函不动，说明是泛函达到了极值，也就说明达到了最佳的时间和状态。当然如果泛函中包含控制，必然会有控制的变分，但本文中脉冲作用被视为状态的间断而非控制量。

分部积分式(5)最后一项得

(6)

定义Hamilton函数为

H=λTf

(7)

并考虑到状态量的变分和自变量有关，有

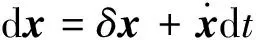
(8)

这里认为自变量t的微分等于变分。

将式(6)～(8)代入式(5)得

(9)

最优性必要条件应该由极值的基本必要条件确定，即要求泛函J(或J的等价泛函J*)的一阶变分为0，即

δJ*=0

(10)

并且不依赖于dtj-、dt(j-1)+、dxj-、dx(j-1)+和δx的选择。通过使δx的系数为0，获得Euler-Lagrange方程

(11)

Euler-Lagrange方程是描述协变量演化的微分方程，和状态方程相对应，也称为协变量方程。

其它系数和每段端点有关，令dtj-、dt(j-1)+、dxj-、dx(j-1)+的系数为0得到一般性的最优边界条件为

(12)

(13)

(14)

(15)

式(12)、式(13)和确定最优状态有关，式(14)、式(15)和确定最优时间有关。式(14)和式(15)在t(j-1)+和tj-时刻分别得到了Hamilton函数的两个边界条件。

与Bryson给出的关于内点时刻tj的一个条件相比，在讨论起始时刻t0+和终端时刻tf-时，式(14)和式(15)更为明确，因为这样避免了涉及t0-和tf+这些实际不存在的时刻点。内点(即脉冲作用点)在上述方程中只是作为一个普通的端点处理，内点和其它端点(始、末端点)可以满足统一的方程形式。

内点的一阶必要条件和Lawden条件相同，但Lawden必要条件没有给出端点(初始时刻和终端时刻)一阶必要条件，而在间接法中，端点和内点的必要条件可以从同一组方程中导出。相对Bryson和Ho[4]以及Lawden[11]给出的内点方程而言，本文的Hamilton边值问题方程更通用，由此也反映了更本质的边值条件解析结构。具体问题的最优性必要条件均可以从本文给出的通用方程中较方便地推出，避免了以往构造边值问题复杂繁琐的困难。

需要说明的是，本文构造的含内点约束的多点边值问题(Multi-pointboundaryvalueproblem，MPBVP)总能得到和未知量相同数目的边界条件，具体原因分析如下：

1)式(12)～(15)中μ包含的每个Lagrange乘子都为常数，由于μ和约束ψ对应，所以它的个数等于ψ所包含约束的个数。问题求解过程中，为了减少未知量的个数，一般会通过一些代数手段消掉Lagrange乘子。

2)式(12)、(13)能够为初始状态x0+和初始协变量λ0+提供数目相等的边界条件(j分别等于f和0)。

3)式(14)、(15)能够为t(j-1)+和tj-提供数目相等的边界条件。

4)式(12)、(13)能够为内点未知量提供数目相等的边界条件。

3 仿真校验

本节采用三个典型算例来测试上文给出的HBVP通用模型，分别是霍曼转移、异面变轨和多脉冲交会。

由于球坐标形式比直角坐标形式物理概念更为直观，而且下文也会展示采用球坐标形式时，其中一个协变量始终为常值，因此本文算例采用球坐标运动方程。只考虑地球引力，航天器的运动方程和对应的协变量微分方程为[12]

(16)

(17)

(18)

(19)

(20)

(21)

λvθ(-vrvθ+vθvφtanφ)+λφv+

(22)

(23)

(24)

(25)

(26)

(27)

3.1 霍曼转移

第一个例子是共面圆轨道之间的轨道转移问题。考虑初始轨道为半径r0=8000 km的环火星圆轨道，目标轨道为半径rf=15000 km的圆轨道。这个问题同Abdelkhalik和Mortari[13]采用遗传算法结合最速下降法计算脉冲轨道转移的第一个算例相同，该算例源自文献[14]。Brown[14]解析证明了此问题最优解的总速度增量为0.609km/s，转移时间为5.2h。

目标函数为总的速度增量最小，最大化性能指标写为

(28)

式中：下标“0”、“2”和“f”分别表示第一次脉冲之前、第二次脉冲时间之前和之后的状态。初始和终端条件分别为

(29)

r2=rf

(30)

根据式(13)和式(28)得边值条件

(31)

(32)

根据式(12)和式(28)得边值条件

(33)

(34)

由于终端时刻自由，根据式(14)得Hamilton函数边值条件

H2=0

(35)

由式(29)和式(13)得，λr1=μr1，其中μr1是对应等式约束r1=r0的Lagrange乘子，所以λr1是未知参数。θ0的取值是任意的，不妨设θ0=0；由于终端条件不限制θ，有λθ2=0，结合式(23)可知，λθ是一个等于0的常数。综上，式(29)～(35)给出了8个边界条件。优化模型的设计变量为8个，分别为Δt、r1、θ1、vr1、vθ1、λr1、λvr1和λvθ1，其中下标“1”表示第一次脉冲之后的状态，未知量和设计变量的数目相等，上述优化问题被转化为两点边值问题。

本文中边值问题求解方法采用解析同伦方法，采用这种方法可以从具有解析解的初始构造问题出发，通过调整参数逐步迭代过渡到原始优化问题，因此这种方法的优势是可以避免协变量初值的猜测的困难，从而比较容易求解边值问题。由于边值问题求解不是本文的研究重点，方法的原理参见文献[12]，此处不再赘述。最终得到协变量初值为λr1=0.268，λvr1=0，λvθ1=1，计算所得结果如表1所示，和理论上的霍曼转移解析解相同。Abdelkhalik和Mortari[13]报告了一个接近霍曼转移的次优解，其中所需速度增量和时间分别为0.6093km/s和5.157h，和最优解的偏差分别为0.033%和0.83%。需要指出，Abdelkhalik和Mortari[13]所计算的霍曼转移最优飞行时间5.08h有误，应为5.2h，见表1。

图1描述了终端时间自由时的最优解主矢量变化历史，显然满足主矢量必要条件。可见，采用间接法能够得到满足主矢量条件的最优解。

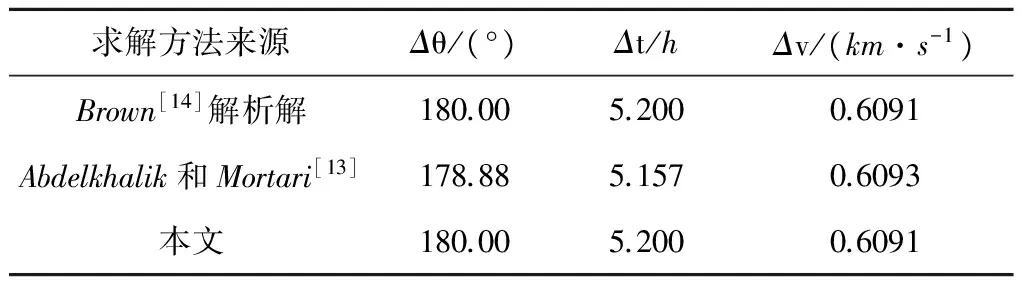
表1 霍曼转移问题求解结果

图1 霍曼转移问题最优解的主矢量变化历史Fig.1 Primer history of the optimal LEO to HEO transfer

3.2 异面变轨

第二个例子是异面圆轨道之间的轨道转移问题。 考虑初始轨道为半径为6671.53km的地球停泊圆轨道，轨道倾角28.5°，目标轨道为半径26558.56km的圆轨道，轨道倾角为0°。这个问题同Abdelkhalik和Mortari[13]采用遗传算法结合最速下降法计算脉冲轨道转移的第二个算例相同，该算例源自文献[15]。Vallado[15]提供了两脉冲最优异面变轨的解析解法。

目标函数为总的速度增量最小，最大化性能指标写为

(36)

式中：下标“0”、“2”和“f”分别表示第一次脉冲之前、第二次脉冲时间之前和之后的状态。

考虑这个问题的一种限制性情况，即限制转移航天器初始时刻在两个轨道的交线上，则φ0=0、vr0=0、vθ0=vc1cosi、vφ0=vc1sini，其中vc1和i分别表示初始轨道的速度大小和轨道倾角，不妨设θ0=0。初始和终端条件分别为

(37)

(38)

根据式(13)和式(36)得边值条件

(39)

(40)

(41)

根据式(12)和式(36)得边值条件

(42)

(43)

(44)

和前面的共面转移问题类似，有

H2=0

(45)

且λθ恒等于0，

(46)

式中：μr1和μφ1是引入的Lagrange乘子，是未知参数。

综上，式(37)～(45)给出了12个边值条件。优化模型的设计变量分别为Δt、r1、θ1、φ1、vr1、vθ1、vφ1、λr1、λφ1、λvr1、λvθ1和λvφ1，其中下标“1”表示第一次脉冲之后的状态。可见，设计变量的个数和边界条件的个数相等，上述优化问题被转化为两点边值问题。

边值问题求解方法同样采用解析同伦方法，得到的协变量初值为λr1=0.757，λφ1=6.16×10-8，λvr1=-6.84×10-8，λvθ1=0.975，λvφ1=0.224，计算结果如表2所示。本文方法能够得到和理论最优解相同的结果，并且优于采用遗传算法结合最速下降法获得的结果(总的速度增量为4.0610km/s[13])和采用伪谱法获得的结果(总的速度增量为4.0594km/s[16])，见表2。图2描述了终端时间自由时的最优解主矢量变化历史，显然满足主矢量必要条件。

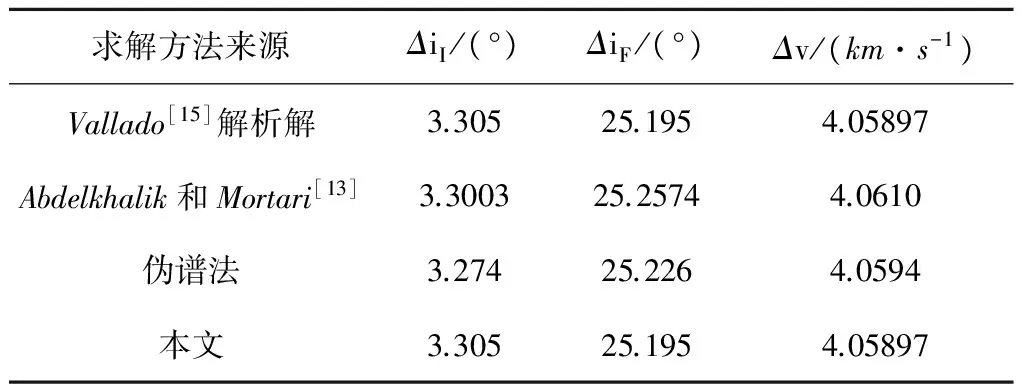
表2 异面变轨问题求解结果

图2 异面变轨问题最优解的主矢量变化历史Fig.2 Primer history of the optimal noncoplanar transfer

3.3 多脉冲交会

同圆交会问题是一个比较经典的多圈脉冲交会问题。目标和追踪航天器是在同一个圆轨道上，追踪航天器滞后目标航天器一定的相位角，要求在一定时间内追踪航天器与目标航天器在该圆轨道上交会(相对状态为0)。图3是目标航天器在追踪航天器前方180°的示意图。关于这个交会问题的研究已经很多，包括Prussing和Chiu[17]、Colasurdo等[18]、Prussing[19]以及Luo等[20-21]，当交会时间是2.3个轨道周期时，上述研究分别报告了最优四脉冲交会解，而且该交会问题需要一个非常大的Δv(大于1200 m/s)。为了便于对比，本文也选择一个400 km圆轨道工况进行测试。

多脉冲交会问题的HBVP最优性条件推导方法和前两个问题类似，因此推导过程这里不再重复，而是直接给出设计结果，特别是主矢量变化结果，从中可以观察解的最优性必要条件的满足情况。

第一个四脉冲最优解主矢量变化见图4(图中黑点表示脉冲作用点)，显然满足Lawden条件。需要指出，这个四脉冲最优解虽然满足主矢量条件，但并不是可行解，因为航天器飞行轨迹最小距离小于地球半径(见图5)。

第二个四脉冲最优解主矢量变化见图6(图中黑点表示脉冲点)，显然满足Lawden条件。这组四脉冲解不但满足主矢量条件，而且也是可行解，图7给出了航天器飞行轨迹在赤道面内的投影，可见最小距离大于地球半径。

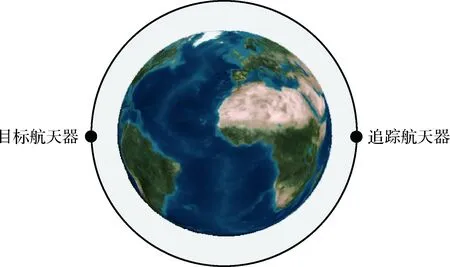
图3 追踪和目标航天器在同一圆轨道上交会问题Fig.3 Illustration of the same-circle rendezvous problem

图4 同圆交会问题第一个解主矢量(算列1)Fig.4 Primer history of same-circle rendezvous (case 1)

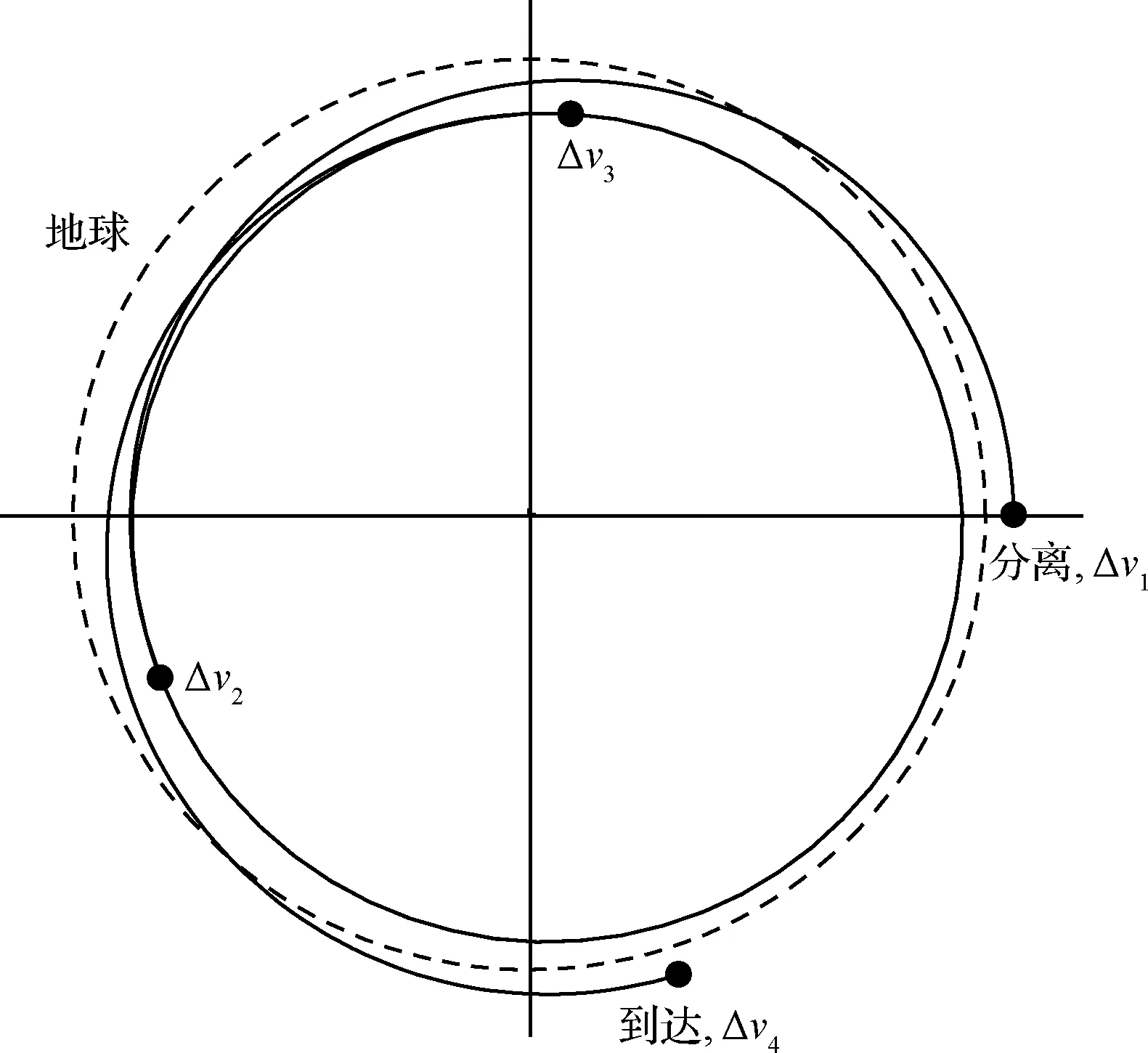
图5 同圆交会问题第一个四脉冲解最优轨迹(算列1)Fig.5 Optimal solution of same-circle rendezvous (case 1)

图6 同圆交会问题第二个解主矢量(算列2)Fig.6 Primer history of same-circle rendezvous (case 2)

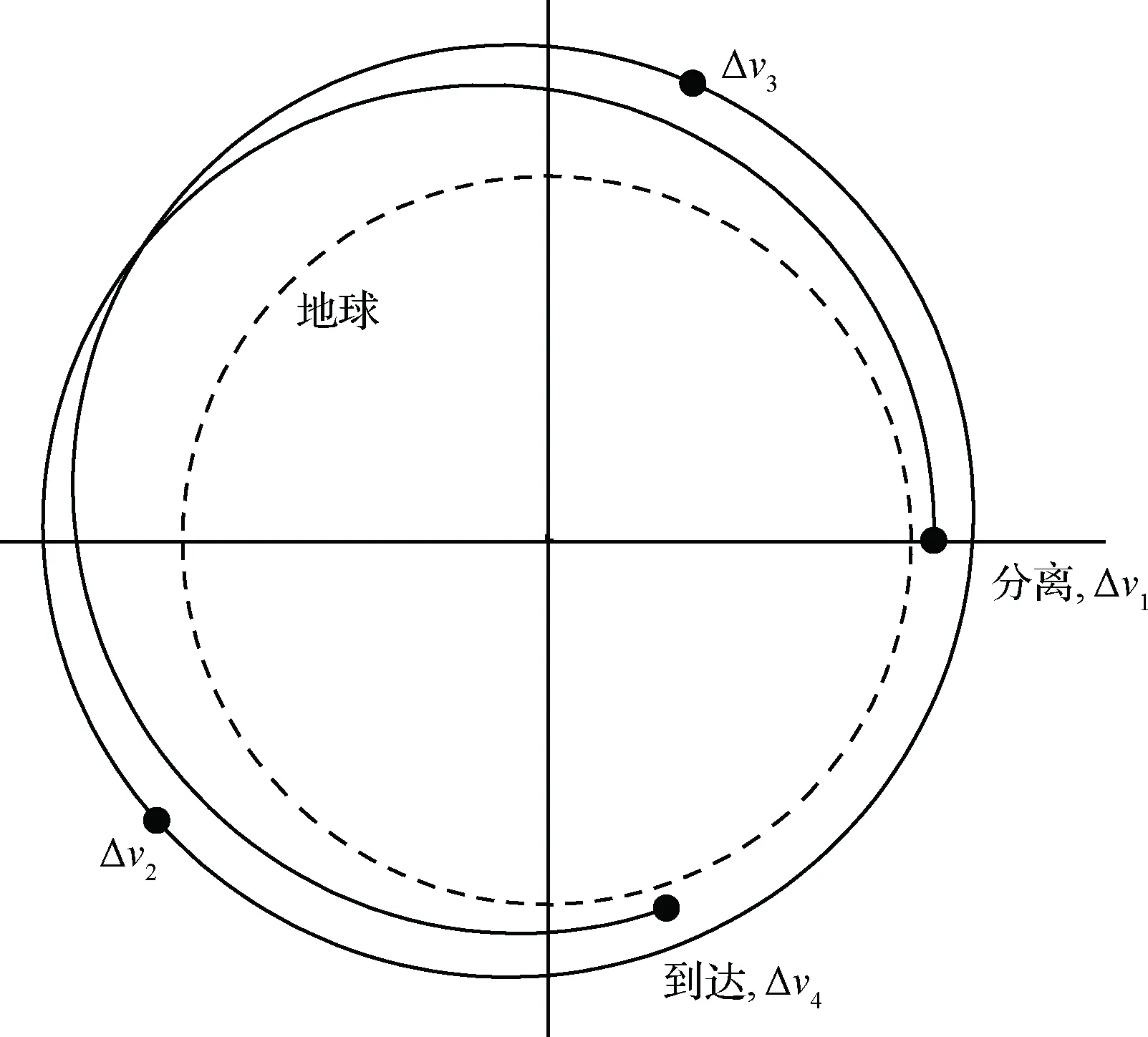
图7 同圆交会问题第二个四脉冲解最优轨迹(算列2)Fig.7 Optimal solution of same-circle rendezvous (case 2)

Prussing和Chiu[17]最早对同圆交会问题进行了研究，但只给出了第二个四脉冲最优解。Colasurdo等[18]采用间接法并结合动力学辅助分析首次完整给出了上述两个四脉冲最优解。Luo等[20]和Luo等[21]利用进化算法也找到了上述两个四脉冲最优解，然而进化算法通常需要的计算较大。相比之下，本文提出的方法较为简单通用，而且能从理论上保证解的最优性。

需要说明的是，初始和终端时刻不能作为内点处理，而且终端时刻可能不固定(见前两个算例)，因此主矢量理论不适用于这两个端点，本文构造的模型可以将端点和内点统一起来处理。

以上三个算例都比较典型，代表了不同类型的轨道转移问题：前两个算例有解析解，一个是平面转移，另一个是异面转移，第三个算例是典型的多脉冲交会问题，不存在解析解。用不同类型的问题能够更好地验证文中模型的适用性。其他脉冲转移问题的Hamilton边值问题的构建与此类似。Lawden主矢量理论是在二体模型中推导的，本文提出的Hamilton边值问题通用模型并不依赖于二体动力学模型假设，对更加复杂的动力学问题也有应用前景。

表3 400 km同圆交会轨道问题的二组解

4 结 论

本文研究了大推力航天器最优飞行路径的Hamilton边值问题，给出了这类问题所满足的边值条件一般形式。根据边值条件的一般形式，可以很方便地得到具体问题的边值条件，从而简化了原问题的复杂性。在讨论最优飞行路径Hamilton边值问题的过程中，发现内点和所有其它端点均可以满足同样一套方程，据此，拓展和完善了Bryson和Ho求解该问题的模型。由于采用了脉冲假设，这个假设只适用于大推力情形，对于小推力问题，是否存在比较通用的边值条件形式还值得进一步研究。

[1] 雍恩米, 陈磊, 唐国金. 飞行器轨迹优化数值方法综述[J]. 宇航学报, 2008, 29(2): 397-406. [Yong En-mi, Chen Lei, Tang Guo-jin. A survey of numerical methods for trajectory optimization of spacecraft [J]. Journal of Astronautics, 2008, 29(2): 397-406.]

[2] 李俊峰, 蒋方华. 连续小推力航天器的深空探测轨道优化方法综述[J]. 力学与实践, 2011, 33(3): 1-6. [Li Jun-feng, Jiang Fang-hua. Survey of low-thrust trajectory optimization methods for deep space exploration [J]. Mechanics in Engineering, 2011, 33(3): 1-6.]

[3] Betts J T. Survey of numerical methods for trajectory optimization [J]. Journal of Guidance, Control, and Dynamics, 1998, 21(2): 193-207.

[4] Bryson A E, Ho Y C. Applied optimal control[M]. Washington, DC: Hemisphere, 1975.

[5] Peng H J, Gao Q, Wu Z, et al. Symplectic approaches for solving two-point boundary-value problems [J]. Journal of Guidance Control and Dynamics, 2012, 35 (2): 653-658.

[6] 陈琪锋,张跃东,吴文昭,等. 基于近似生成函数迭代的分布式卫星构形最优控制研究[J]. 宇航学报, 2009, 30(3): 988-993. [Chen Qi-feng, Zhang Yue-dong, Wu Wen-zhao, et al. Research on optimal control of distributed satellite system formation based on iteration of generating function approximation [J]. Journal of Astronautics, 2009, 30(3): 988-993.]

[7] Jiang F, Baoyin H, Li J. Practical techniques for low-thrust trajectory optimization with homotopic approach [J]. Journal of Guidance, Control, and Dynamics, 2012, 35(1): 245-258.

[8] Shen H X, Casalino L, Li H Y. Adjoints estimation methods for impulsive Moon-to-Earth trajectories in the restricted three-body problem [J]. Optimal Control Applications and Methods, 2014, 36: 463-474.

[9] Pan B, Lu P, Pan X, et al. Double-homotopy method for solving optimal control problems [J]. Journal of Dynamic Systems, Measurement and Control, 2016, 39(8): 1706-1720.

[10] Hwang I, Li J H, Du D. Differential transformation and its application to nonlinear optimal control [J]. Journal of Dynamic Systems, Measurement and Control, 2009, 131(5): 1-11.

[11] Lawden D F. Optimal trajectories for space navigation [M]. London: Butterworths, 1963.

[12] 沈红新. 基于解析同伦的月地应急返回轨迹优化方法[D]. 长沙：国防科技大学, 2014. [Shen Hong-xin. Optimization method for the Moon-Earth abort return trajectories based on analytic homotopic technique [D]. Changsha: National University of Defense Technology, 2014.]

[13] Abdelkhalik O, Mortari D. N-impulse orbit transfer using genetic algorithms [J]. Journal of Spacecraft and Rockets, 2007, 44(2): 456-460.

[14] Brown C D. Spacecraft mission design[M]. AIAA, 1998.

[15] Vallado D A. Fundamentals of astrodynamics and applications[M]. Torrance, USA: Microcosm Press, 2001.

[16] Shen H X. A novel algorithm for optimal design of impulsive orbit transfer [C]. The 3rd International Symposium on Systems and Control in Aeronautics and Astronautics, Harbin, China, June 8-10, 2011.

[17] Prussing J E, Chiu J H. Optimal multiple-impulse time-fixed rendezvous between circular orbits [J]. Journal of Guidance Control and Dynamics, 1986, 9(1):17-22.

[18] Colasurdo G, Pastrone D. Indirect optimization method for impulsive transfer[R]. AIAA Paper 1994-3762, 1994.

[19] Prussing J E. A class of optimal two-impulse rendezvous using multiple-revolution Lambert solutions [J]. The Journal of the Astronautical Sciences, 2000, 48(2):131-148.

[20] Luo Y Z, Zhang J, Li H Y, et al. Interactive optimization approach for optimal impulsive rendezvous using primer vector and evolutionary algorithms[J]. Acta Astronautica, 2010, 67(3): 396-405.

[21] Luo Y Z, Tang G J, Li Y J, et al. Optimization of multiple-impulse, multiple-revolution, rendezvous phasing maneuvers [J]. Journal of Guidance, Control, and Dynamics, 2007, 30(4): 946-952.

[22] Shen H X, Casalino L. Indirect optimization of three-dimensional multiple-impulse Moon-to-Earth transfers [J]. The Journal of Astronautical Sciences, 2014, 61: 255-274.

通信地址：西安505信箱28分箱(710043)

电话：(029)84762520

E-mail:shxnudt@163.com

Hamilton Boundary Value Problem for Optimal Impulsive Trajectory

SHEN Hong-xin

(State Key Laboratory of Astronautic Dynamics, Xi’an Satellite Control Center, Xi’an 710043, China)

For a spacecraft with high thrust, a general equations based on variational calculus for formulating the Hamilton boundary value problem (HBVP) is proposed, where the optimality conditions on interior points and other general boundary points (inclucling initial and final points) are in the same manners, so that our equations tend to reveal the more intrinsic analytic structure of HBVP. The detailed optimality conditions can be determined conveniently according to the general equations; therefore, the tedious task of formulating HBVP is precluded. Simulations show that the method proposed in this paper could ensure obtaining the optimal flight path of the high-thrust spacecraft effectively and efficiently.

Boundary value problem; Optimality; Interior point; Impulsive trajectory

2016-10-18;

2017-05-15

V412.4

A

1000-1328(2017)07-0686-08

10.3873/j.issn.1000-1328.2017.07.000

沈红新(1986-)，男，博士，工程师，主要从事航天器轨道姿态最优控制研究。