J2项摄动下的远程拦截耗尽关机中制导律设计

呼卫军，王 欢，周 军

(西北工业大学精确制导与控制研究所，西安 710068)



J2项摄动下的远程拦截耗尽关机中制导律设计

呼卫军，王 欢，周 军

(西北工业大学精确制导与控制研究所，西安 710068)

为实现远程高精度动能拦截，针对使用固态燃料发动机的拦截弹在强时间约束下的耗尽关机问题，本文设计一种基于通用能量管理(GEM)的闭环中制导律。该制导律首先考虑了地球非球形J2摄动项对弹道影响，改进Lambert问题求解算法，在小计算量的情况下修正了因地球扁率摄动在远程拦截长时段飞行过程中引起的需求速度求解偏差，将其精度提升一个数量级。然后在GEM基础上给出了一种能量调制角虚拟映射关系实现了能量调制初段指令平滑过渡，并改变近关机点推力定向策略解决了临近关机时指令发散问题。在制导过程中加速度计反馈环节的引入增强了对推进系统参数的鲁棒性。六自由度仿真表明，相比传统GEM制导律，该制导律精度更高，任务适应性强。

通用能量管理(GEM)；Lambert问题；地球扁率；需求速度；虚拟映射

0 引 言

随着航天技术迅速发展，弹道导弹逐渐向多个国家扩散，形势日益严峻。多国开始着手构建导弹防御体系。自美国进行地基中段防御(Ground missile defense,GMD)试验以来，由于该类技术具备拦截早，拦截概率高，附带伤害少等优点，研究开始逐渐升温。鉴于我国正处于多种弹道导弹射程范围，而尚未形成防御体系，因此开展远程中段拦截高精度中制导策略研究对于保障国家安全具有重要的战略意义。

远程拦截弹中制导段一般指助推末级到经数千公里无控飞行后捕获到目标的飞行阶段，因此，中制导律设计需要完整考虑弹目间引力差。显然，基于零控脱靶量(ZEM)的中制导律[1-4]因利用弹目引力差简化模型，精度不足。而引入现代控制理论所设计的最优中制导律[5]往往假设拦截器可连续控制，难以直接应用。文献[6]将引力差模型进一步拓展，给出了远程拦截场景零控拦截流形[7]描述，但并未设计相应制导律。为应对远程来袭弹道导弹，基于椭圆方程以飞行时间为约束对两点边值问题快速求解所设计的Lambert制导律[8]被广泛应用，但考虑到固体燃料推进系统情况，中制导律设计还需进一步引入能量管理环节，实现拦截弹的耗尽关机。

目前涉及能量管理的远程拦截中制导主要分两类：一类为迭代制导律[9-11]，主要通过多层迭代，寻求拦截弹剩余速度增益与需求速度相匹配拦截点，任务适应能力差。另一类为能量管理制导律，主要通过设计不同的能量管理策略耗散多余燃料，其中开环能量管理制导律[12-13]需提前设计调整策略，易受干扰影响且精度较低。而闭环能量管理制导律中，基于零射程线[14-17]中制导律对发动机参数偏差鲁棒强，但是忽略拦截强时间约束属性，不能直接应用。虽然基于反馈线性化的动态逆能量管理(IEM)[18]策略可控能量耗散强度，但未充分考虑推进系统参数偏差。剩余速度增量虚拟映射[6]的引入为提高制导精度对装药燃速偏差的鲁棒性提供新的思路。

通用能量管理(General energy management,GEM)策略[8]简单而准确，但为实现远程动能拦截，地球扁率影响以及关机点附近姿态角变化剧烈等问题有待解决。因此为减小制导误差，对地球非

球形摄动因素测算必不可少。文献[6]采用数值积分

对地球J2项摄动修正，计算量大。而文献[19-20]与文献[21]分别给出了J2项摄动影响下自由飞行弹道解析解，但形式复杂，同样不适用于在线解算。

综上分析，本文将以GEM为基础，针对远程拦截弹固体火箭推进方式，首先考虑剩余飞行时间约束与长时段无控滑行时地球摄动影响，高精度快速求解需求速度，在此基础上期望设计一种基于拦截弹剩余速度增量信息显式中制导律。不仅实现闭环能量管理，使得关机时刻耗尽多余能量的情况下精确达到零控拦截流形状态，而且发动机推力方向变化平稳，对推进系统参数鲁棒，同时能明显改善末段拦截环境，提高系统拦截精度。

1 拦截弹需求速度求解

1.1 基于Lambert定理的需求速度求解

(1)

(2)

(3)

式(1)为命中方程，表征了弹目地心距比、速度大小V以及弹道倾角γ之间的关系。

因Lambert问题涉及超越方程，无解析解。经验证[7]，可通过牛顿迭代法对γ迭代实现飞行时间t到treq的快速收敛，求解出V即为拦截弹需求速度大小VN。但若所求速度VN达到逃逸速度，不可达PIP点，因此本文限定拦截弹沿椭圆弹道飞行[8]即λ<2。进一步确定γ上下界(γmin,γmax)

(4)

1.2 地球非球形摄动影响下的需求速度求解

对比其他引力摄动，地球非球形J2摄动影响至少高出两个数量级[20]，因此本文仅引入地球J2摄动修正需求速度。该摄动影响下拦截弹道实际偏差示意图见图1。

图1 地球扁率摄动示意图Fig.1 Schematic diagram of the earth oblateness perturbation

取J=1.5J2，aE为赤道半径，并定义拦截弹当前地心矢径r1与PIP点地心矢径r2所决定的平面为参考拦截平面，其对应的地心距为r1与r2，地心纬度分别φ1与φ2，Δλ为两点间经差。设φ为当前点纬度，r、β和βf与图1设定一致，ψ=ψ(β)为参考拦截面与摄动弹道平面的球心角，引入余纬度σ=π/2-φ参量，则J2摄动项函数为：

(5)

本节将基于文献[20]在小耦合常数J中，围绕参考拦截平面所拆分的参考拦截面内与法向方向摄动展开项，结合第1.1节理想引力场解算公式，改进传统的需求速度求解方法。

假设拦截弹无控飞行，根据所取摄动得出在参考拦截面与其法向方向的拉格朗日运动方程，确定出参考拦截面内、拦截面法向方向以及飞行时间关于地球扁率J一阶项的摄动微分方程[20]：

(6)

(Bcosβ+Csinβ)

(7)

(8)

式中：U=1/r,p=r1Vcosγ为未扰动情况下拦截弹角动量，σ可利用以下球面三角关系式替换：

cosσ= cosβsinφ1+sinβcosφ1×

(1-cos2φ2sin2Δλ/sin2βf)0.5

(9)

B、C、g(β)满足以下关系：

(10)

ε为地球圆球模型角动量小扰动，满足：

(11)

下面通过合理的假设，对式(6)、(7)、(8)分别求解，实现拦截弹需求速度高精度求解。

1.2.1 改进的飞行时间补偿求解

因飞行时间摄动较小，其补偿值可与理想引力场中t分开求解。为更精确求解，式(8)右侧假设r以平均地心距ra代替，而不是关机点地心距r1，即：

ra=

(12)

可见ra的求解与式(3)中的tf相关项相同，并未增加计算量。代入dε/dβ表达式到方程，仅取摄动项，得tOB微分方程

(13)

推导出补偿时间表达式[20]：

(2βf-sin2βf)-BCsin2βf]

(14)

则整个自由段飞行时间即可表示为tTotal=tf+tOB。

1.2.2 拦截面内修正速度求解

拦截面内式(6)右侧r取拦截弹初始地心距r1，设无量纲λ=r1V2/μE，忽略o(J2)，则：

U(β)=U1(β)+JU2(β)

(15)

式中：

(16)

式中：

有别于文献[20]中以拦截弹到达PIP点的地心距r2为约束，完全求解摄动影响下的需求速度VO，本文充分利用第1.1节需求速度VN与弹道倾角γN求解结果仅对需求速度摄动项ΔVN修正，取无量纲参数λN=r1V2/μE，因存在U2(β)摄动项，当β=βf时：

(17)

此时存在射程角小的偏差项Δβf,使得：

(18)

因此对球扁率摄动在参考拦截面内对地心距的影响定量分析转换到射程角偏差项Δβf，可由U(β)对β的微分关系近似确定：

(19)

将式(1)和式(16)代入式(19),得：

(20)

利用无摄动时拦截弹自由飞行误差系数相关方程[22]可得出ΔVN与Δβf关系：

(21)

最终在无摄动情况下需求速度VN与弹道倾角γN求解基础上，通过式(19)、式(20)与式(21)解算参考拦截面内修正速度ΔVN，最终需求速度为：

VO=VN+ΔVN

(22)

1.2.3 拦截面法向方向修正速度求解

地球扁率引起的法向运动是小量，可独立求解。文献[20]已求解出法向修正速度VCOB：

[Csinβf+βf(Bsinβf-Ccosβf)]

(23)

其速度的修正方向垂直于拦截平面，由沿r1方向的单位矢量ur和垂直于r1且在参考拦截面内顺β增大方向的单位矢量uβ确定，即ur×uβ。

1.2.4 地球非球形摄动影响下的速度求解流程

本节参考理想引力场中需求速度求解流程，在考虑地球J2摄动情况下仅将补偿项tOB纳入迭代，而需求速度补偿项ΔVN与VCOB跳出循环后一次求解，几乎不增加计算量，即可最终确定需求速度矢量VN。具体设计流程如图2所示：

图2 需求速度求解流程Fig.2 Demand speed solving process

1.3 仿真校验

取aE=6378140 m，设定拦截弹当前高度h=100 km，经纬度分别为Bm=40°与λm=117°。设定射程为2000km，假设地球不自转，到J2摄动项且忽略气动力，以10°为间隔对发射方位角20°～60°范围内取值。以4s为间隔对最小能量弹道倾角对应的飞行时间±16s内取值。以数值积分弹道作为参考标准值，得脱靶量与飞行时间偏差量，并根据当前组最大脱靶量MissMax与最大飞行时间偏差ΔtfMax作归一化处理，验证需求速度改进算法的有效性。表1给出了最大的脱靶量和飞行时间偏差。

表1 最大偏差值

根据仿真结果绘制改进前后对比如图3所示。图3(a)为需求速度求解改进后脱靶量对比图。图3(b)为改进前后飞行时间偏差量对比图，并补充飞行时间补偿方程右侧取r=r1时飞行时间偏差(中间平面)与本文方法作对比。由图3可以看出：

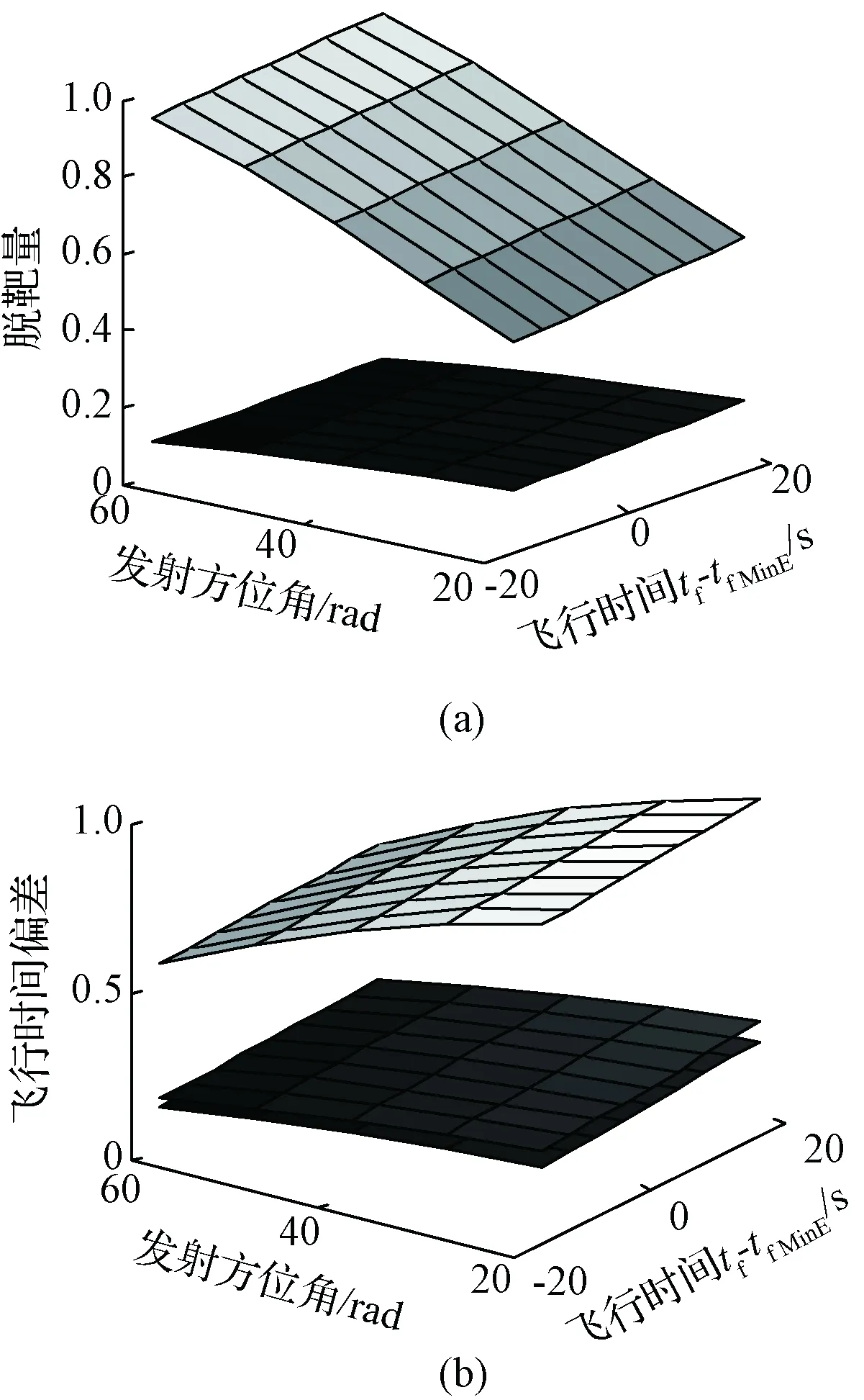
图3 2000 km射程脱靶量与飞行时间偏差仿真结果Fig.3 Simulation results of miss distance and flight time deviation under the condition of 2000 km Range

1)相比传统Lambert方法，本文需求速度求解改进后脱靶量与飞行时间的精度提高了一个数量级，且拦截弹即使自由飞行2000km，对目标点脱靶量也仅在0.5km内，保证在末制导修正范围之内。

2)对比式(14)给出的飞行时间补偿方程右侧取r=r1时结果可知，本文方法在此基础上解算精度提高近10%。

2 耗尽关机中制导律设计

2.1 通用能量管理策略(GEM)

需求速度VN确定后，本文将针对拦截弹末级助推耗尽关机情况，基于GEM策略通过实时引入剩余速度增量Vcap设计中制导律实现当前速度矢量Vcur对VN高精度稳定跟踪。考虑图4空间矢量关系：

图4 GEM中基本角度关系Fig.4 The basic angle relationship in GEM

图4中α为总攻角，OAB为Vcur与VN所成平面。g为当前重力矢量，Vg为待增速度矢量，即：Vg=VN-Vcur。γ为推力矢量T与Vcur所成平面与平面OAB间二面角，且η为VN与Vg间夹角。圆弧半径暂设为rθ，弦长为待增速度模量Vg，假设在圆弧的起点，T沿弧线切线方向与Vg间的夹角θ为调制角，且圆心到弦长垂线等分弦长与圆心角，同时取Pg=Vg/Vcap。

由Vcap=2rθθ与Vg=2rθsinθ关系，通过泰勒公式展开到二阶近似项，可得

(24)

该方程意味着在中制导段每一瞬时，T与Vg始终呈夹角θ，当发动机能量耗尽时刻，拦截弹当前速度Vcur刚好达到需求速度VN。证明如下：

求Pg关于发动机工作时间t一阶导为下式：

(25)

(26)

取cosθ二阶近似值，并代入式(26)替换θ得：

(27)

设拦截弹发动机关机时刻为toff，当前时刻为t，基于瞬时假设：若发动机在t以后工作时间内aT保持常值，则在t时刻有下式成立：

(28)

因此，式(27)可变换为：

(29)

设发动机点火时刻为t0，则Pg取Pg0，设Pg在(t0,Pg0)之后有解，则在t0后的动态方程为：

(30)

再次对Pg求导得

(31)

(32)

2.2 剩余速度增量Vcap求解

(33)

式中:Isp为推进剂真空比冲，g0为标准重力加速度大小，mbo为发动机耗尽时拦截弹质量，m0为拦截器中制导初始质量。

2.3 姿态定向

上文仅对平面内夹角θ解算，但三维空间姿态定向不唯一。因此本文参考文献[23]中“燃料最省”意义下准最优导引方案：基于g与Vg确定T方向，将三维空间约束到二维平面。如图4所示，设ζ为g与Vg之间的夹角，则T满足约束：

(34)

虽然该策略因能量调制过程中存在夹角γ，使得拦截弹速度矢量绕VN旋转，其旋转角速度为：

(35)

但考虑到θ基于剩余速度增量Vcap反馈求解，随着能量消耗，在Vg>0时有θ→0，T趋于与Vg重合，即γ→0，ω收敛到0，避免在关机点附近俯仰，偏航指令角高频振荡，设计合理。

2.4GEM改进策略

2.4.1 调制初段改进策略

由式(24)可知，当中制导初始段Vcap较多，初始θ较大，易引起发动机摆动喷管饱和。为降低对Pg敏感度，适应大范围能量管理，本文引入θ的变系数虚拟映射值θvir。以下给出一种映射关系：

(36)

式中：N为指数项，取值为：

(37)

式中：t为发动机已工作时间，tsd为发动机标称工作时间，n、k为调节系数。n项期望实现较小调制角θ起控，k项能使得姿态平稳过渡后，N快速收敛至0，θ恢复正常求解值，避免因n造成的初段低能量耗散率导致末段θ角速率过大。

为说明映射关系的特点，不妨设Pg与t存在线性关系，且初值为Pg0：

(38)

不失一般性，设定Pg0=0.7，tsd标称时间60s，通过对n与k取不同值作仿真分析。

由图5可以看出,n与k变化时，θvir与θ之间关系。k越大，θvir越慢恢复到θ正常求解值，越不利于制导中末段耗能，因此一般取小值。更重要的是该策略除tsd可提前获取外，并未引入新误差源。

2.4.2 近关机点改进策略

在拦截场景中，Vg并非线性变化，满足方程[23]：

(39)

式中：Q需求速度VN对当前地心距矢量r的偏导，Q=∂VN/∂r是3×3矩阵。

根据第2.3节姿态定向策略，当θ收敛到0后，GEM收敛为闭路制导。临近关机时，因Vg→0，其方向快速转向QVg，导致关机点附近姿态发散。为

图5 映射系数对θvir影响Fig.5 Influence of mapping coefficient on θvir

图6 近关机点推力控制示意图Fig.6 Near close-off point thrust control diagram

姿态角指令变化规律为:

(40)

3 仿真校验

本节参考地基拦截弹GBI(Ground based interceptor)助推第三级，参数见表2(其中各通道转动惯量根据典型几何体转动惯量公式求解)。以逆轨拦截为例，建立六自由度仿真模型，对所设计中制导律从指令平滑性、拦截任务适应性以及发动机参数偏差鲁棒性进行综合分析。

表2 拦截弹三级参数

3.1 指令平滑性分析

为验证中制导律指令平滑性，设拦截弹发射点经纬度：λ0=-121.69°、B0=48.48°，三级116 s点火。初始俯仰角与偏航角分别为0.595 rad与0 rad，滚转角始终为零且各通道初始姿态角速度均为0。飞行时间约束取984 s。以5 ms步长仿真，记录关机点速度跟踪偏差Vgend与最终脱靶量Dmiss，并绘制变化较为明显的俯仰角指令和实际俯仰角速度曲线。表3给出116s时拦截弹发惯系及目标地惯系PIP点状态。

表3 拦截弹与目标状态

3.1.1 近关机点改进策略指令平滑性校验

选取不同增益系数k1对比传统GEM策略，验证近关机点推力控制改进策略。表4给出了近关机点策略改进后的对比效果。

表4 近关机点仿真对比结果列表

图7 改进前后俯仰角指令与实际俯仰角速度对比图Fig.7 The comparison chart for improvement of the pitch angle command and the actual pitch angle speed

根据科图7的仿真结果可以看出，k1的选取对改进效果有显著影响，通过对k1合理取值，可抑制末端姿态角指令的发散，有利于拦截弹后续分离与姿态稳定。图7(a)和图7(b)分别给出了俯仰角和俯仰角速率改进和无改进的对比效果图。

3.1.2 调制初段改进策略指令平滑性校验

基于第3.1节结果，取近关机点增益k1=0.01，添加能量调制初段改进策略，对调制角θ虚拟映射参数n与k选不同参数，因俯仰角指令与图5相似，仅绘制俯仰角速度说明该策略的有效性。表5给出了调制初段改进的结果列表。

表5 调制初段改进结果列表

图8 n与k取不同值时实际俯仰角速度对比结果Fig.8 The actual pitch angle speed comparison result when n and k take different values

通过当前拦截场景的仿真结果(图8)可知：

1)引入调制角θ虚拟映射，不影响需求速度跟踪精度，且明显改善俯仰通道的指令平滑度；

2)通过图8(a)与初始俯仰角对比可以看出，n越大，起控阶段指令越平滑，实际飞行中俯仰角速度越小。由图8(b)可知，k越大，调制角θ越慢恢复到正常求解值，在调制后段较之k取较小值情况，会产生相对较大的角速度。

3.2 任务适应性分析

首先定义G0=Vcap0/Vg0表征多余燃料量，其中Vcap0为中制导段初始速度增量，Vg0为初始待增速度模量。本节将根据设定不同飞行时间约束求解出的G0验证所设计的中制导律能否适应远程拦截任务中因目标存在测量误差或是机动变轨引起的剩余速度增量需求变化情况。中制导段系数取n=1.5，k=1/3，k1=0.01。按照不同的时间约束G0,表6给出了不同参数下的仿真结果。

由图9可知，即使当G0值较大，因加入虚拟映射，依然能满足待增速度收敛精度。但n或k越大，θ收敛到标称值越慢，耗能效率越低，因此对映射系数n、k取值应根据实际拦截任务取值。

3.3 制导律鲁棒性分析

发动机参数偏差也是制约制导精度关键因素。一般推进剂总冲可在地面较精确控制，本文将忽略。

表6 不同任务仿真结果列表

图9 不同耗能情况下调制角θ与待增速度Vg收敛特性Fig.9 Convergence characteristics of θ and Vg in different energy consumption

图10 加速度测量环节引入前后速度跟踪偏差/脱靶量对比Fig.10 Speed tracking deviation and distance miss before and after acceleration measurement introduced

3.3.2 推力线偏移鲁棒性分析

为研究摆动喷管摆角与指令角度值存在随机偏差时导致的推力线偏移对需求速度跟踪精度的影响，图11给出了制导策略改进前后主发动机摆动喷管摆角在俯仰方向的变化曲线。

图11 摆动喷管俯仰/偏航通道摆角变化Fig.11 The change of pitch and yaw pendulum angle of nozzle

由图11可知，改进前后俯仰通道摆角大幅度降低，最大摆角仅δφ=2°左右且经起控阶段后主发动机摆角维持在零附近。当摆角δφ=2°时，若偏移量为摆角的20%，(0.4°)，对应三角函数值：

(41)

因此，该量级对推力线方向分量几乎无影响。

4 结 论

由上述结果综合分析可知,在典型的拦截场景中，本文设计的耗尽关机中制导律不仅可以平滑指令，而且在应对大耗能的情况时，能满足最终的需求速度跟踪精度，经自由段飞行后仅存在较小的脱靶量，而且该制导律对发动机秒耗量偏差与推力线偏移鲁棒性强，对提升远程拦截效能具有重要的实际意义。

[1] Brett N. Strategic intercept midcourse guidance using modified zero effort miss steering[J]. Journal of Guidance, Control and Dynamics, 1996, 19(1): 107-112.

[2] Yan N G, Matt H, Bong W. Applications of generalized zero effort miss/zero effort velocity feedback guidance algorithm[J]. Journal of Guidance, Control and Dynamics, 2013, 36(3): 810-821.

[3] 郑立伟, 荆武兴. 大气层外拦截器近最优中制导律设计[J]. 宇航学报, 2008, 29(1):229-235.[Zhen Li-wei, Jing Wu-xing. Design a near optimal midcourse guidance law for exo-atmospheric interceptor[J]. Journal of Astronautics, 2008, 29(1): 229-235.]

[4] 郑立伟, 荆武兴，张建英. 适用于大距离拦截问题的零控脱靶量计算方法[J]. 宇航学报, 2007, 28(4):865-869.[Zhen Li-wei, Jing Wu-xing, Zhang Jian-ying. Zero effort miss formulation for longer range targeting[J]. Journal of Astronautics, 2007, 28(4): 865-869.]

[5] Fu K Y, Hsiuan H C, Li C F. Nonlinear optimal sliding mode midcourse controller with thrust vector control[C]. Proceedings of the American Control Conference, Anchorage, AK, May 8-10, 2002.

[6] 刘世勇, 吴瑞林, 周伯昭. 大气层外拦截弹中段制导研究[J]. 宇航学报, 2005, 26(2):156-163.[Liu Shi-yong, Wu Rui-lin, Zhou Bo-zhao. Research on midcourse guidance for fuel-exhaustion-shutoff exo-atmospheric interceptor[J]. Journal of Astronautics, 2005, 26(2): 156-163.]

[7] 韩京清.拦截问题中的导引律[M].北京：国防工业出版社,1977.

[8] Zarchan P. Tactical and strategic missile guidance[M]. Progress in Astronautics and Aeronautics, AIAA, Washington DC, 2002.

[9] 陈峰，肖业伦，陈万春. 基于零控脱靶量的大气层外超远程拦截制导[J]. 航空学报，2009, 30(9): 1583-1589.[Chen Feng, Xiao Ye-lun, Chen Wan-chun. Guidance based on zero effort miss for super-range exo-atmospheric intercept[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(9): 1583-1589.]

[10] Steven P B, Jeff J S. Lambert guidance routine designed to match position and velocity of ballistic target[J]. Journal of Guidance, Control and Dynamics, 2004, 27(6): 989-996.

[11] WhiteJ E. Guidance and targeting for the strategic target system[J]. Journal of Guidance, Control and Dynamics, 1992, 15(6): 1313-1319.

[12] Patha J T, Mcgehee R K. Guidance, engery management, and control of a fixed-impluse solid-rocket vehicle during orbit transfer[R]. AIAA Paper 1976-1920,1976.

[13] 姚党鼐, 张力, 王振国. 姿态角单次调整固体火箭耗尽关机能量管理方法[J]. 国防科技大学学报, 2013, 35(1):39-42.[Yao Dang-nai，Zhang Li，Wang Zhen-guo. Depleted shutdown energy management approach for solid launch vehicle with singular attitude angle adjustment[J]. Journal of National University of Defense Technology, 2013, 35(1): 39-42.]

[14] De S, Thomas W. Cut-off insensitive guidance[D]. Massachusetts: Massachusetts Institute of Technology, 1971.

[15] 周军, 潘彦鹏, 呼卫军. 固体火箭的鲁棒自适应耗尽关机制导方法研究[J]. 航天控制, 2013, 31(3): 34-39.[Zhou Jun, Pan Yan-peng, Hu Wei-jun. A robust and adaptive depleted shutdown guidance method of solid rocket[J]. Aerospace Control, 2013, 31(3): 34-39.]

[16] Sang J K, TaeY U. Flight-path angle control for cut-off insensitive guidance[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(4): 706-710.

[17] Dwivedi P N, B A, Padhi R. Suboptimal mid-course guidance of interceptors for high-speed targets with alignment angle constraint[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(3): 860-877.

[18] 张志健, 王小虎. 固体火箭多约束耗尽关机的动态逆能量管理方法[J]. 固体火箭技术, 2014, 37(4): 435-462.[Zhang Zhi-jian, Wang Xiao-hu. Inverse dynamic energy management for multi-constrained depleted shutdown of solid rocket[J]. Journal of Solid Rocket Technology, 2014, 37(14): 435-462.]

[19] Dean Z. Exo-atmospheric intercept with J2 correction[C]. Guidance, Navigation, and Control Conference and Exhibit, Boston, USA, August 10-12, 1998.

[20] Levine S A. Effect of oblateness in explicit guidance[R]. Massachusetts Institute of Technology Instrumentation Lab, August 1963.

[21] 李连仲. 弹道飞行器自由飞行轨道的解析解法[J]. 宇航学报, 1982, 1(1):1-17.[Li Lian-zhong. An analytic method for solving the equations of free flight trajectory of ballistic vehicle[J]. Journal of Astronautics, 1982, 1(1): 1-17.]

[22] Wheelon A D. Free flight of a ballistic missile[J]. ARS Journal, 1959, 29(12): 915-916.

[23] Battin R H. Space guidance evolution-a personal narrative[J]. Guidance Journal, 1982, 5(2): 97-110.

Design of Mid-Course Guidance Law Considering J2 Perturbation for Long-Range Fuel-Exhaustion-Shutoff Interceptor

HU Wei-jun, WANG Huan, ZHOU Jun

(Institute of Precision Guidance and Control, Northwestern Polytechnical University, Xi’an 710068, China)

In order to realize remote and high precision kinetic energy interception, a closed-loop mid-course guidance law based on general energy management (GEM) is designed to solve the problem of the exhaustion shut down of an interceptor with solid fuel engine under strong time constraints. In this paper, the impact of the non-spherical J2 perturbation on the trajectory is firstly considered to improve the algorithm of the Lambert problem and correct the deviation of the demand velocity caused by the Earth oblateness perturbation in the long-range interception, elevating the demand velocity accuracy by an order of magnitude. Then, an energy modulation angle virtual mapping relationship is presented based on the GEM to achieve the attitude command smooth transition during the energy modulation initial stage. And the near-off point thrust direction strategy is changed to solve the command divergence problem. The introduction of the accelerometer feedback in the guidance process enhances the robustness to the propulsion system parameters. Six-degree-of-freedom simulation shows that this guidance law is more accurate and adaptable than the conventional GEM guidance law.

General energy management (GEM); Lambert problem; Earth oblateness; Demand velocity; Virtual mapping

2016-10-10;

2017-04-21

国家自然科学基金(61473226); 西北工业大学基础研究基金(F030107)

V412 4

A

1000-1328(2017)07-0694-10

10.3873/j.issn.1000-1328.2017.07.000

呼卫军(1979-)，男，博士，副教授，主要从事导弹制导控制技术、先进控制理论及其应用和飞行器数字仿真技术等研究。 通信地址：西安市友谊西路127号234信箱(710068)